柯西矩阵介绍
经典定义
柯西矩阵(Cauchy Matrix),是一种特殊类型的矩阵,它在数学中的多个领域,包括线性代数、数值分析和插值理论中都有重要应用。柯西矩阵以19世纪法国数学家奥古斯丁-路易·柯西的名字命名。
柯西矩阵是一个方阵,其元素由下面的表达式给出:
C i j = 1 x i − y j C_{ij} = \frac{1}{x_i - y_j} Cij=xi−yj1
其中 x i x_i xi 和 y j y_j yj 是两组实数或复数,且满足 x i ≠ y j x_i \neq y_j xi=yj对所有 i ≠ j i \neq j i=j都成立。这里的 i i i 和 j j j 分别表示矩阵的行索引和列索引,且 i , j = 1 , 2 , … , n i, j = 1, 2, \ldots, n i,j=1,2,…,n。
柯西矩阵的一些重要性质包括:
- 非奇异性:只要 x i x_i xi和 y j y_j yj 都是互不相同的,柯西矩阵是非奇异的,也就是说它是可逆的。
- 行列式:柯西矩阵的行列式可以通过一种特殊的公式来计算,这个公式表明行列式的值取决于 x i x_i xi 和 y j y_j yj的差异。
- 逆矩阵公式:柯西矩阵的逆矩阵也有特定的结构和表达式,可以通过代数方法求得。
柯西矩阵在插值和逼近理论中尤为重要,因为它们与多项式插值相关。在构造柯西矩阵时选择的 x i x_i xi和 y j y_j yj可以看作是在复平面上的点,且这些点用于定义插值多项式的分母。这种矩阵的特殊结构使得它们在数值稳定性方面表现优秀,对于解决插值问题和系统方程十分有用。
此外,由于柯西矩阵具有良好的条件性质,即便在计算机数值计算中容易产生舍入误差的环境下,使用柯西矩阵进行运算仍然可以得到比较准确的结果。
柯西矩阵还出现在多项式理论中,特别是在研究多项式的零点时。例如,柯西矩阵与Vandermonde矩阵紧密相关,这在理论研究和应用领域如信号处理中都非常重要。
广义定义
在数学中,柯西矩阵的概念可以扩展到非方阵的情况。一个广义的柯西矩阵是由两组数 x i i = 1 m {x_i}_{i=1}^m xii=1m_和 _ y j j = 1 n {y_j}_{j=1}^n yjj=1n 定义的一个 m × n m \times n m×n 矩阵,其中 m m m 和 n n n 可以不相等。矩阵的元素由以下公式给出:
C i j = 1 x i − y j C_{ij} = \frac{1}{x_i - y_j} Cij=xi−yj1
在这里, x i x_i xi 是第一组数中的第 i i i个元素, y j y_j yj 是第二组数中的第 j j j个元素,且条件是对所有的 i i i 和 j j j,有 x i ≠ y j x_i \neq y_j xi=yj 以确保分母不为零。
非方阵的广义柯西矩阵仍然保留了柯西矩阵的一些关键性质,包括:
- 元素结构:每个元素都是两个数的差的倒数,这种结构在数值分析和多项式插值中特别有用。
- 低秩更新:当 x i x_i xi 或 y j y_j yj发生小的变化时,整个矩阵的变化可以通过低秩矩阵更新来描述,这在迭代算法和数值方法中是一个有用的性质。
- 特殊的行列式和逆矩阵:虽然非方阵没有行列式或逆矩阵,但对于方阵的子矩阵,相关性质仍然适用。例如,如果我们从广义柯西矩阵中选取一个正方形的子矩阵,那么这个子矩阵将具有与经典柯西矩阵相同的行列式和逆矩阵计算公式。
广义柯西矩阵在多项式插值中的应用尤为突出,特别是在构建插值基函数时。插值问题通常涉及构造一个多项式或者一系列基函数,使得这个多项式在一系列给定点的值与要插值的函数的值相匹配。如果我们选择广义柯西矩阵中的 x i x_i xi作为插值点,那么可以利用柯西矩阵的性质来构建具有良好数值稳定性的插值方案。
此外,广义柯西矩阵还可以出现在最小二乘逼近问题、系统和控制理论中的稳定性分析,以及复分析中的某些问题中。在这些情况下,柯西矩阵的性质可以被用来简化计算,提高算法的效率和稳定性。
应用
柯西矩阵因其特殊性质在算法应用上具有广泛用途,特别是在数值分析、线性代数和多项式逼近等领域。以下是一些具体的算法应用:
- 多项式插值:在多项式插值中,柯西矩阵用于构建插值多项式,尤其是在有理插值中,它可以用来确定插值多项式的系数,以便多项式在一组给定的点上取特定的值。
- 求解线性方程组:当线性方程组可以表示成柯西矩阵时,可以利用柯西矩阵的特殊逆矩阵公式和性质来高效地求解这些方程组。
- 系统和控制理论:在系统和控制理论中,柯西矩阵可以用来分析系统的稳定性,尤其是在控制器设计和状态估计中。
- 信号处理:柯西矩阵在信号处理中的应用包括系统识别和通道估计等领域。在这些应用中,柯西矩阵有助于从有噪声的测量中恢复信号或系统参数。
- 计算数值积分:在数值分析中,柯西矩阵有时用于计算特定类型积分的数值方法,尤其是当被积函数涉及到分母项时。
- 逼近理论:在逼近理论中,柯西矩阵可以用于最小二乘逼近问题,其中柯西型的核函数用于构造逼近函数。
- 图像和视频压缩:在图像处理中,柯西矩阵有时用于压缩算法,其中柯西型分布可以作为数据矩阵的低秩近似。
- 编码理论:在编码理论中,柯西矩阵的性质用于构建纠错码,如里德-所罗门码(Reed-Solomon codes),它们用柯西矩阵来构造生成矩阵和校验矩阵。
- 密码学:柯西矩阵在密码学中也有应用,特别是在秘密共享方案中,柯西矩阵的性质有助于分发秘密信息的分片。
这些仅仅是柯西矩阵在算法和应用领域的一部分实例。由于其逆矩阵、行列式和其他性质的数学优雅,柯西矩阵在许多需要复杂数值计算和稳定算法的领域都非常有用。
相关文章:

柯西矩阵介绍
经典定义 柯西矩阵(Cauchy Matrix),是一种特殊类型的矩阵,它在数学中的多个领域,包括线性代数、数值分析和插值理论中都有重要应用。柯西矩阵以19世纪法国数学家奥古斯丁-路易柯西的名字命名。 柯西矩阵是一个方阵&am…...
PureFlash v1.9.1特性介绍
PureFlashv1.9.1版本特性主要有4个: 1. 支持RDMA网络 使用RDMA协议可以大大减少对CPU的消耗,性能提升30%以上。 PureFlash的网络配置分为存储节点间网络(存储后端网)和客户端网络(前端网)。都支持使用RD…...
XXE 漏洞简单研究
近期在做个基础的 web 常见漏洞的 ppt,主要参考 OWASP TOP 10 2017RC2,此版本中增加了 XXE 攻击,所以自己简单的研究下 XXE 攻击。XXE(XML External Entity)XML 外部实体,当前端和后端通信数据采用 xml&…...
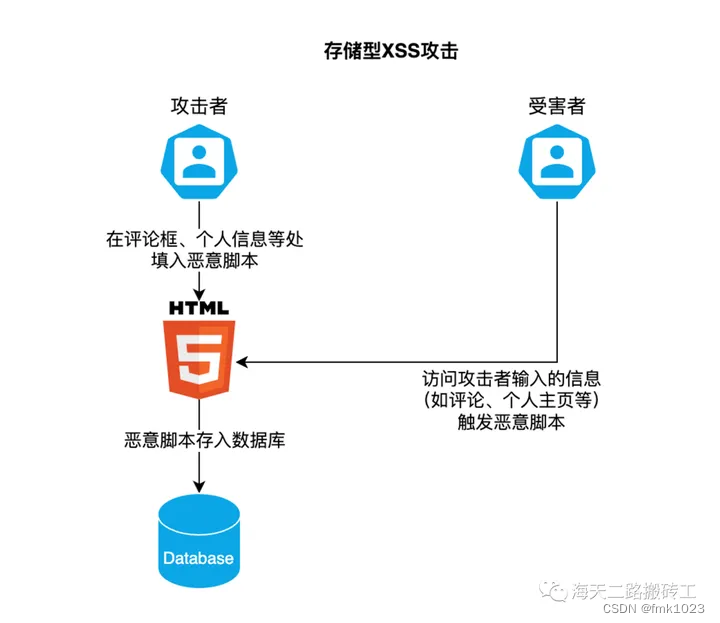
web漏洞与规避
文章目录 一、XSS 跨站脚本攻击1.1 XSS攻击的主要类型反射型XSS存储型XSSDOM型XSS 1.2 前端开发如何应对XSS 二、CSRF 跨站请求伪造2.1 CSRF例子2.2 前端开发如何应对CSRF 三、SQL 注入3.1 前端如何防御SQL注入 四、前端如何使用CSP 一、XSS 跨站脚本攻击 攻击者通过在受害者的…...

#FPGA(基础知识)
1.IDE:Quartus II 2.设备:Cyclone II EP2C8Q208C8N 3.实验:正点原子-verilog基础知识 4.时序图: 5.步骤 6.代码:...

LockBit病毒入侵揭秘:如何防范与应对
在数字时代,随着科技的飞速发展,网络安全问题愈发凸显。恶意软件和勒索软件等网络威胁正不断演变,其中一款备受关注的勒索软件就是LockBit。本文将深入介绍LockBit的特征、攻击手段、演进历程以及对网络安全的威胁。 01 主要特征 LockBit是…...
vue-router4 (六) 路由嵌套
应用场景: ①比如京东页面的首页、购物车、我的按钮,可以点击切换到对应的页面; ② 比如 Ant Design左侧这些按钮点击就会切到对应的页面,此时可以把左侧按钮放在父路由中,右侧的子路由 1.路由配置,子路由…...
【NR 定位】3GPP NR Positioning 5G定位标准解读(一)
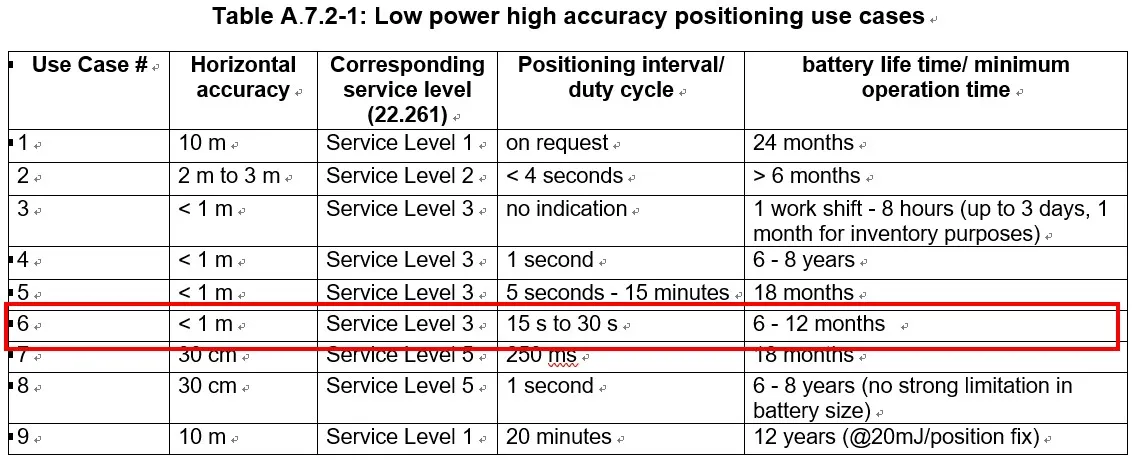
目录 前言 1. 3GPP规划下的5G技术演进 2. 5G NR定位技术的发展 2.1 Rel-16首次对基于5G的定位技术进行标准化 2.2 Rel-17进一步提升5G定位技术的性能 3. Rel-18 关于5G定位技术的新方向、新进展 3.1 Sidelink高精度定位功能 3.2 针对上述不同用例,3GPP考虑按…...
【AI绘画】免费GPU Tesla A100 32G算力部署Stable Diffusion
免责声明 在阅读和实践本文提供的内容之前,请注意以下免责声明: 侵权问题: 本文提供的信息仅供学习参考,不用做任何商业用途,如造成侵权,请私信我,我会立即删除,作者不对读者因使用本文所述方法…...
JVM(2)
JVM类加载 指的是java进程运行时,需要把.class文件从硬盘加载到内存,并进行一系列校验解析的过程. 核心: .class文件>类对象; 硬盘>内存. 类加载过程 在整个JVM的执行流程中,和程序员关系最密切的就是类加载的过程了,所以我们来看一下类加载的执行流程. 对于一个类…...
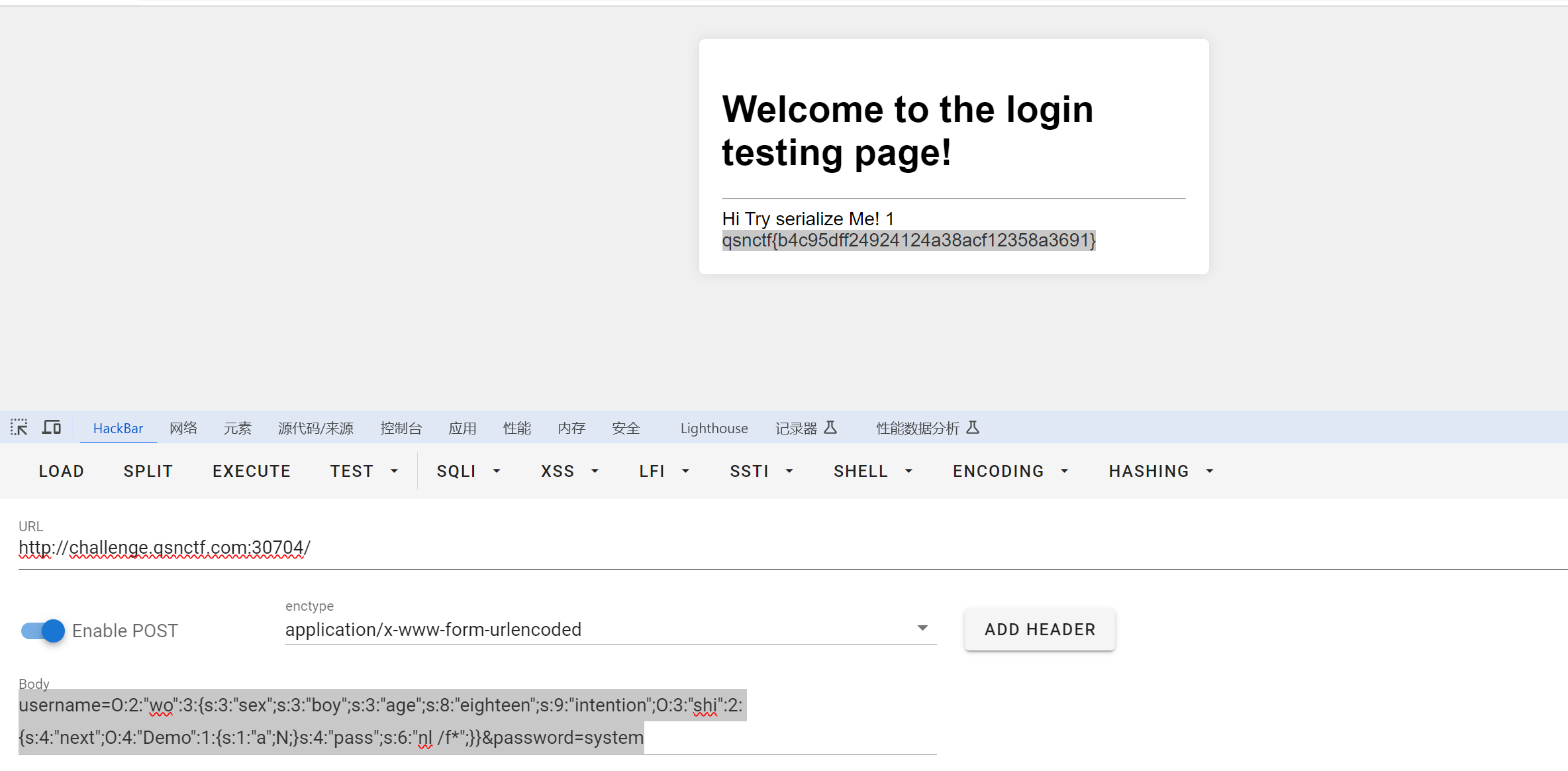
青少年CTF擂台挑战赛 2024 #Round 1 Web方向题解 WP 全
EasyMD5 题目描述:php没有难题 考点总结:脑洞题目,不如我出(狗头 只允许两个都上传pdf文件。 文件还不能太大了。burp多次发包发现要求两个pdf内容不一样 不一样时候,提示我们MD5碰撞。 科学计数法绕过 PHP的后门 …...
一文认识蓝牙(验证基于Aduino IDE的ESP32)
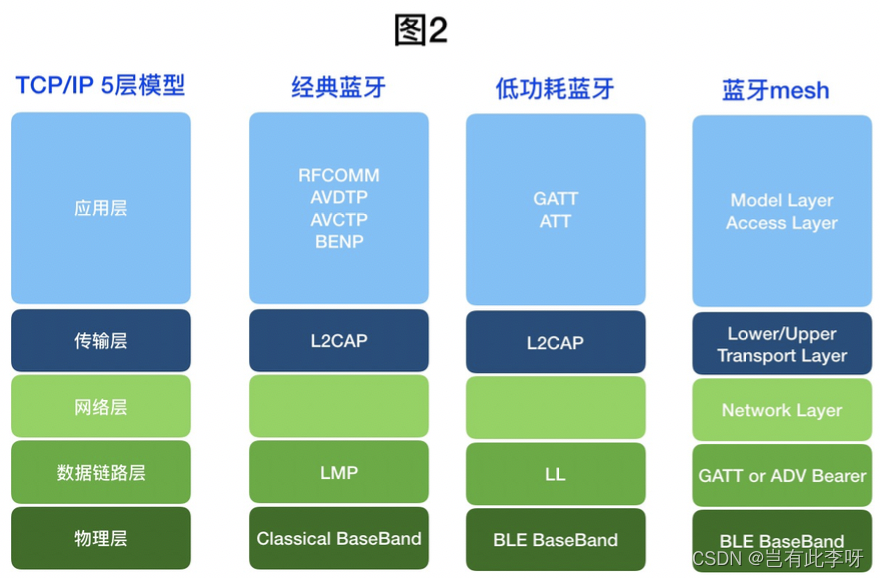
1、简介 蓝牙技术是一种无线通信的方式,利用特定频率的波段(2.4GHz-2.485GHz左右),进行电磁波传输,总共有83.5MHz的带宽资源。 1.1、背景 蓝牙(Bluetooth)一词取自于十世纪丹麦国王哈拉尔Haral…...
2W字-35页PDF谈谈自己对QT某些知识点的理解
2W字-35页PDF谈谈自己对QT某些知识点的理解 前言与总结总体知识点的概况一些笔记的概况笔记阅读清单 前言与总结 最近,也在对自己以前做的项目做一个知识点的梳理,发现可能自己以前更多的是用某个控件,以及看官方手册,但是没有更…...
Docker知识点总结
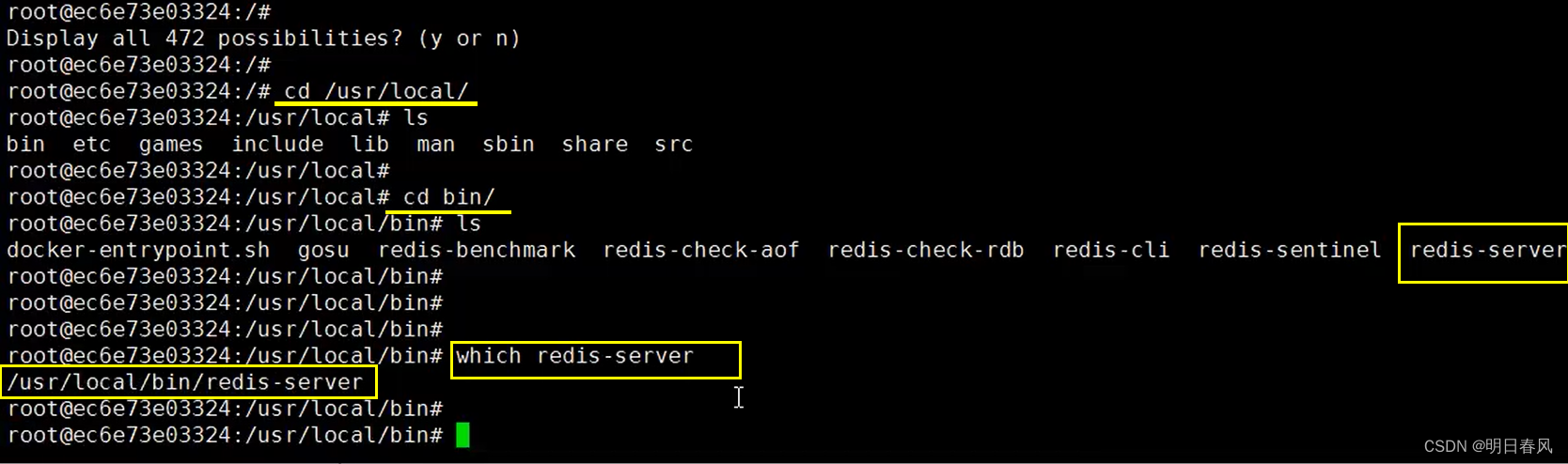
二、Docker基本命令: Docker支持CentOs 6 及以后的版本; CentOs7系统可以直接通过yum进行安装,安装前可以 1、查看一下系统是否已经安装了Docker: yum list installed | grep docker 2、安装docker: yum install docker -y -y 表示自动确认…...

Redis 消息队列:构建消息代理的 4 个简单步骤
消息代理是一种使系统、应用程序和服务能够通信和交换信息的软件。它在正式消息传递协议之间转换消息,并允许相互依赖的服务直接“对话”,即使是用不同语言编写或在不同平台上实现也是如此。在微服务中使用异步通信时,通常会使用消息代理。 消息代理可确保可靠且稳定的通信,…...

kafka三节点集群平滑升级过程指导
一、前言 Apache Kafka作为常用的开源分布式流媒体平台,可以实时发布、订阅、存储和处理数据流,多用于作为消息队列获取实时数据,构建对数据流的变化进行实时反应的应用程序,已被数千家公司用于高性能数据管道、流分析、数据集成和任务关键型…...

Golang 简介与基本语法学习
Go,也被称为 Golang,是一门由 Google 设计的开源编程语言。它旨在提供高效的开发体验,同时具备并发性、内存安全和简洁性。本篇博客将介绍 Golang 的基本语法和一些示例,帮助读者快速入门这门令人着迷的语言。 简介 Go 语言的设…...

深入理解网络通信基本原理和tcp/ip协议
深入理解网络通信基本原理和tcp/ip协议 一、计算机网络体系1,计算机网络体系结构2,网络中数据传输2.1,浏览器中输入一个url的执行流程2.2,数据在网络中是的传输流程 3,三次握手和四次挥手3.1,三次握手3.1.1…...
Jetson系统烧录环境搭建
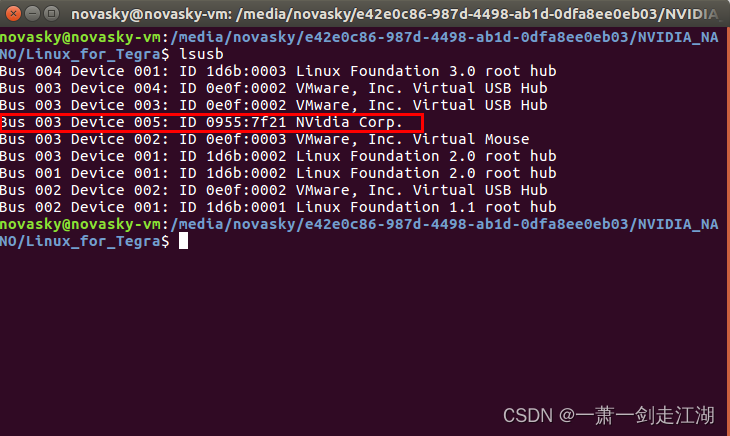
一 序言 Jetson 系列产品烧录系统的方法一般有两种,一种为使用 NVIDIA 官方提供 的 SDK manager 软件给 Jetson 设备烧录系统(请查看说明文档《Jetson 产品使用 SDKmanager 烧录系统》)。另一种即为当前文档所描述的,在安装 Ubun…...

【MySQL】:约束全解析
🎥 屿小夏 : 个人主页 🔥个人专栏 : MySQL从入门到进阶 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一. 约束概述二. 约束演示三. 外键约束3.1 介绍3.2 语法3.3 删除/更新行为 &…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
