贪心(基础算法)--- 区间选点
905. 区间选点
思路
(贪心)O(nlogn)
根据右端点排序
-
将区间按右端点排序
-
遍历区间,如果当前区间左端点不包含在前一个区间中,则选取新区间,所选点个数加1,更新当前区间右端点。如果包含,则跳过。
-
输出所选点的个数。
举例: 为什么不能根据左端点排序呢?
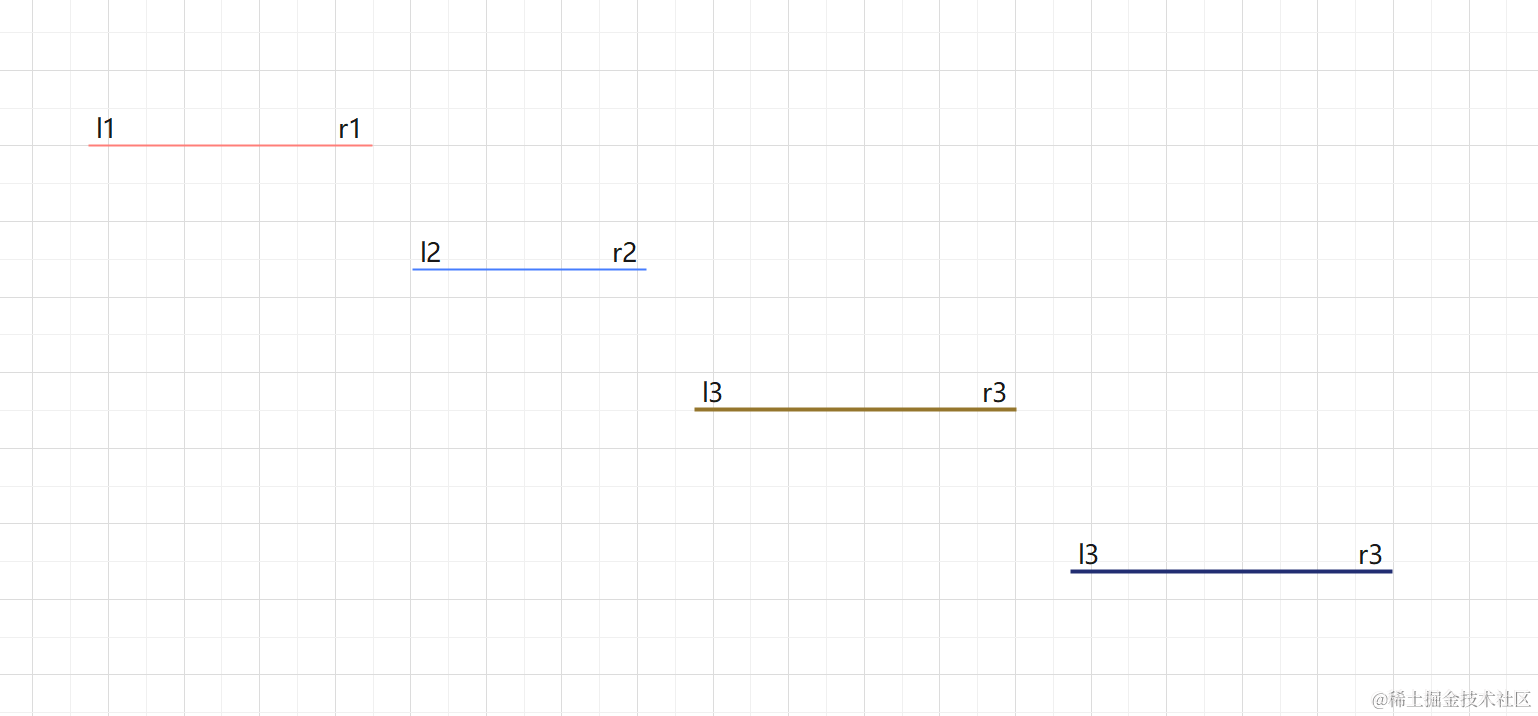
如下图所示,有三个区间

我们按右侧排序是如图所示,l3 > r2,点数加1,更新右端点,l1 < l3,无需更新,直接跳过
如果改成按左侧排序的话,r2 < r1 && r3 < r1,无需更新所需点数,输出点数为1(错误)。
- 第一个区间为
l1~r1, 当我们遍历到l2~r2的时候,没有问题,l2 < r1, 无需更新。 - 但当我们遍历到
l3~r3这个区间的话,就出现问题了,l3 < r1, 无需更新 - 输出点数1

解决办法 :在遍历其他区间的时候,同时更新区间右端点取最小值
Java代码
import java.util.*;
class Range implements Comparable<Range>{int l,r;public Range(int l,int r){this.l = l;this.r = r;}public int compareTo(Range o){return Integer.compare(r,o.r);//return this.r - o.r;}
}
public class Main{static int N = 100010,INF = 0x3f3f3f3f,n;static Range[] range = new Range[N];//结构体创建数组需要定义成全局变量public static void main(String[] args){Scanner scan = new Scanner(System.in);n = scan.nextInt();for(int i = 0 ; i < n ; i ++ ){int l = scan.nextInt();int r = scan.nextInt();range[i] = new Range(l,r);}//结构体排序Arrays.sort(range,0,n); //Arrays.sort(range, 0, n, (o1, o2) -> o1.r - o2.r);int res = 0;//表示一共需要多少点int ed = -INF; // 上一个点的右端点for(int i = 0 ; i < n ; i ++ ){if(range[i].l > ed){res ++ ;ed = range[i].r;}}System.out.println(res);}
}
根据左端点排序
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();List<Pair> v = new ArrayList<>();for(int i = 0; i < n; i ++) {int l = sc.nextInt();int r = sc.nextInt();v.add(new Pair(l, r));}Collections.sort(v, (a, b) -> a.x - b.x);int l = Integer.MIN_VALUE;int r = Integer.MIN_VALUE;int res = 0;for(Pair p : v) {if(p.x <= r) {// l = Math.max(l, p.x);r = Math.min(r, p.y); (每次取r的最小值,本质上其实还是根据右端点进行排序)} else {res += 1;l = p.x;r = p.y;}}System.out.println(res);}}class Pair implements Comparable<Pair> {int x;int y;public Pair(int x, int y) {this.x = x;this.y = y;}@Overridepublic int compareTo(Pair o) {return Integer.compare(this.x, o.x);}
}
正确性证明 :
定义:Ans 为所有可行方案中所需点最小数量,Cnt为当前方案中所需点的数量(一种可行方案)
-
为证明 Ans == Cnt ,我们只需证明 Ans >= Cnt , Ans <= Cnt即可。
-
既然Ans为最小数量,易得Ans <= Cnt。
-
由于我们是根据右端点进行排序遍历,举一个极端例子,由图可知,Cnt等于4,Ans >= 4。
-
Ans >= Cnt &&Ans <= Cnt -> Ans = Cnt。
相关文章:

贪心(基础算法)--- 区间选点
905. 区间选点 思路 (贪心)O(nlogn) 根据右端点排序 将区间按右端点排序 遍历区间,如果当前区间左端点不包含在前一个区间中,则选取新区间,所选点个数加1,更新当前区间右端点。如果包含,则跳…...
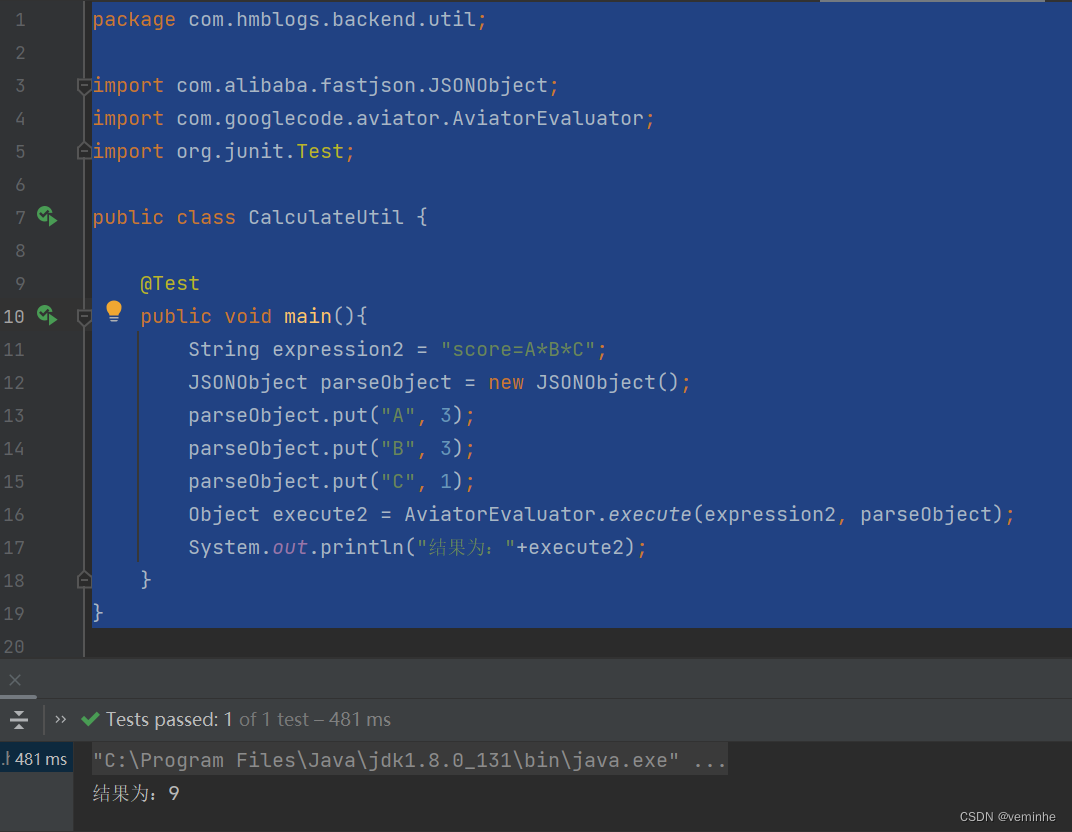
JAVA计算表达式
需求: 1、例如if(score>85){return 1;}else if(score>70){return 2;}else if(score>60){return 3;}else{return 4;}有这一串字符串,要执行这个字符串, 如果score为86分,则能得到1;如果score为30分ÿ…...
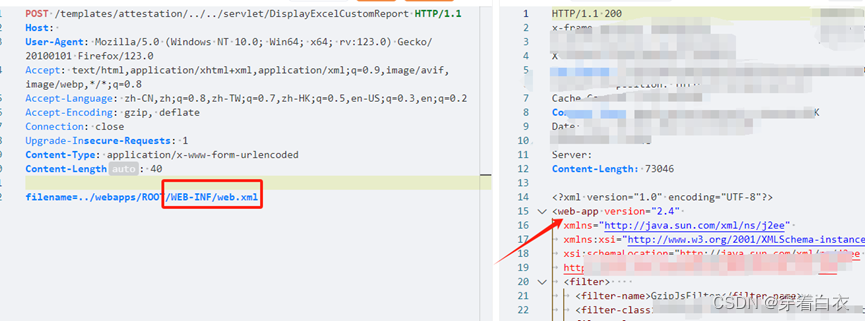
【复现】宏景HCM 任意文件读取漏洞_63
目录 一.概述 二 .漏洞影响 三.漏洞复现 1. 漏洞一: 四.修复建议: 五. 搜索语法: 六.免责声明 一.概述 宏景HCM 将人才标签技术应用于员工招聘、人才选拔等环节,通过多维度的标签体系,形成不同专业序列的人才画…...
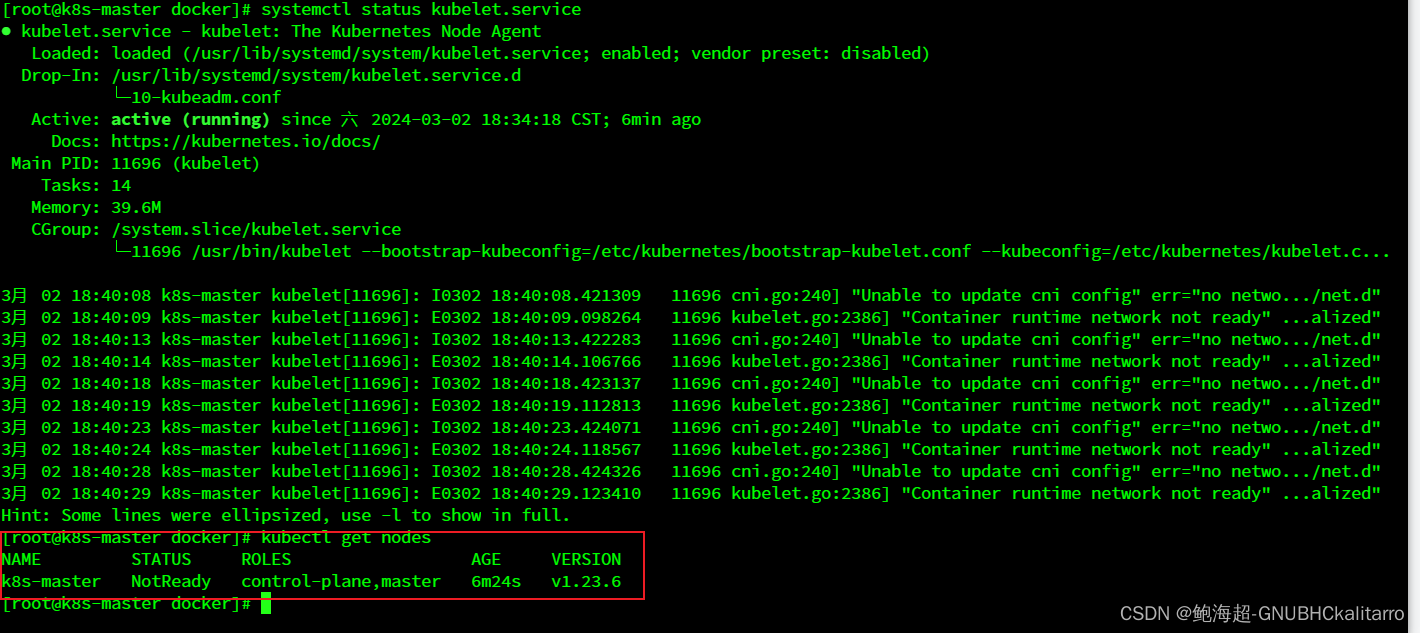
Linux:kubernetes(k8s)搭建mater节点(kubeadm,kubectl,kubelet)(2)
安装k8有多种方式如: minikube kubeadm 二进制安装 命令行工具 我这里就使用kubeadm进行安装 环境 3台centos7 master ip :192.168.113.120 2G运存 2内核 node1 ip :192.168.113.121 2G运存 2内核 node2 ip :192.168.1…...

Web应用安全威胁与防护措施
本文已收录至《全国计算机等级考试——信息 安全技术》专栏 由于极其容易出现漏洞、并引发安全事故,因此数据隐私的保护是目前绝大多数企业不可绕过的运维环节。不过,许多中小型企业往往会错误地认为只有大型企业才会成为黑客的目标。而实际统计数字却截…...

MySQL相关知识汇总
MySQL是一个广泛使用的开源关系型数据库管理系统,它以其高性能、稳定性和易用性而备受开发者喜爱。在软件开发领域,无论是大型项目还是小型应用,MySQL都扮演着重要的角色。本文将对MySQL的一些关键知识点进行汇总,帮助读者更好地了…...

【旧文搬运】为你的 Laravel 应用添加一个基于 Swoole 的 WebSocket 服务
做了一个基于 Swoole 的 WebSocket 扩展包,可以用来做实时状态推送,或者自定义消息处理实现 im,有需要的可以看看: [giorgio-socket] 使用方法 安装 安装扩展包 composer require wu/giorgio-socket发布配置文件 php artisan vendor:pu…...
vue项目从后端下载文件显示进度条或者loading
//API接口 export const exportDownload (params?: Object, peCallback?: Function) > {return new Promise((resolve, reject) > {axios({method: get,url: ,headers: {access_token: ${getToken()},},responseType: blob,params,onDownloadProgress: (pe) > {peC…...
[技巧]Arcgis之图斑四至点批量计算
前言 上一篇介绍了arcgis之图斑四至范围计算,这里介绍的图斑四至点的计算及获取,两者之间还是有差异的。 [技巧]Arcgis之图斑四至范围计算 这里说的四至点指的是图斑最东、最西、最南、最北的四个地理位置点坐标,如下图: 四至点…...

【java】20:枚举
枚举的二种实现方式 1) 自定义类实现枚举 2) 使用 enum 关键字实现枚举 自定义实现枚举: 1.不需要提供setXxx方法,因为枚举对象值通常为只读. 2.对枚举对象/属性使用final static共同修饰,实现底层优化. 3.枚举对象名通常使用全部大写&…...
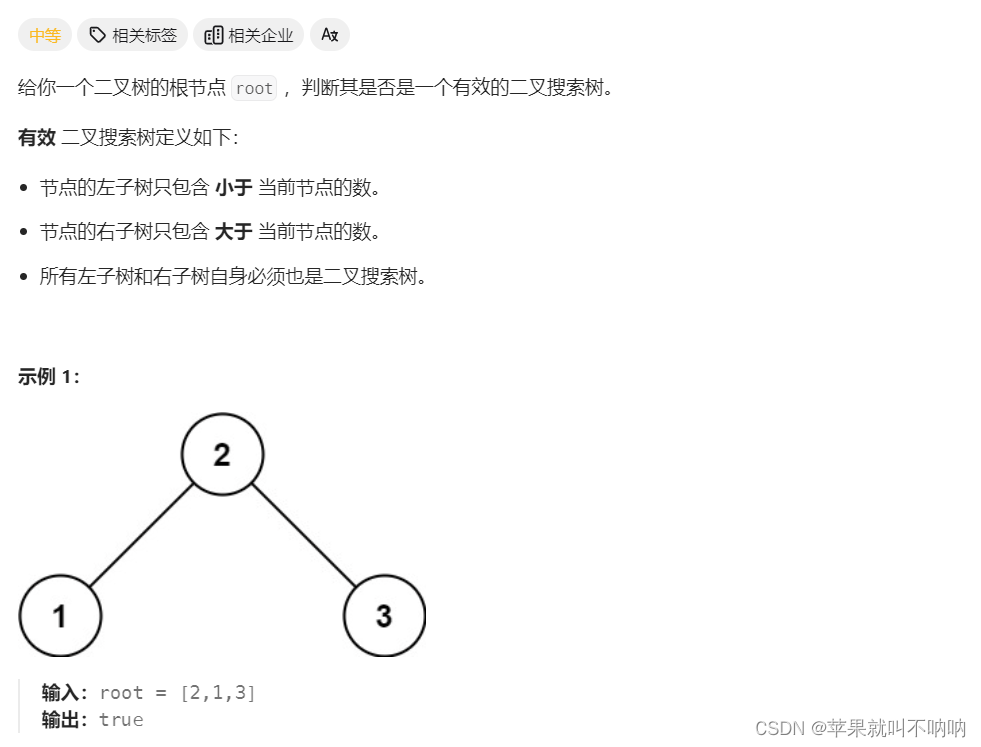
★【二叉搜索树(中序遍历特性)】【 ★递归+双指针】Leetcode 98. 验证二叉搜索树
★【二叉搜索树(中序遍历特性)】【 ★递归双指针】Leetcode 98. 验证二叉搜索树 二叉搜索树 98. 验证二叉搜索树解法1 笨 中序递归遍历为一个数组 然后判断数组是不是升序排列就可以★解法2 不使用数组 递归法 ---------------🎈Ἰ…...
方法实战指南)
打造无缝滚动体验:JavaScript中的scrollIntoView()方法实战指南
在现代Web开发中,提升用户体验是至关重要的。通过JavaScript的scrollIntoView()方法,我们可以为用户创造出流畅而令人愉悦的滚动体验。本文将深入研究scrollIntoView()的强大功能,并结合实例演示如何在项目中巧妙应用,以打造出无缝…...

实战:如何将Oracle单实例数据库转换成Oracle RAC数据库
导读 本文介绍如何将Oracle单实例数据库转换成Oracle RAC数据库 环境说明: 数据库节点2上有个单实例数据库zlxdb2,现在要将zlxdb2转换成RAC数据库,RAC数据库的两个实例分别是lzydb1和lzydb2。 以下是详细的操作步骤: 1、查看zlxdb…...

基于华为atlas的分类模型实战
分类模型选用基于imagenet训练的MobileNetV3模型,分类类别为1000类。 pytorch模型导出为onnx: 修改mobilenetv3.py中网络结构,模型选用MobileNetV3_Small模型,网络输出节点增加softmax层,将原始的return self.linear4…...

编程语言:SQL Server数据库使用教程,SQL Server增删改查语句
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:对网络安全感兴趣的小伙伴可以关注专栏《网络安全自学教程》 SQL Server是微软提供的一种关系型数据库,…...

【tableau学习笔记】tableau无法连接数据源
【tableau学习笔记】tableau无法连接数据源 背景: 学校讲到Tableau,兴奋下载Kaggle Excel,一看后缀CSV,导入Tableau发现报错“tableau无法连接数据源”,自作聪明改为后缀XLSX,bug依旧。 省流:…...
cetos7 Docker 安装 gitlab
一、gitlab 简单介绍和安装要求 官方文档:https://docs.gitlab.cn/jh/install/docker.html 1.1、gitlab 介绍 gitLab 是一个用于代码仓库管理系统的开源项目,使用git作为代码管理工具,并在此基础上搭建起来的Web服务平台,通过该平…...

无极低码:无极低码部署版操作指南
无极低码 :https://wheart.cn 无极低码是一个面向开发者的工具,旨在为开发者、创业者或研发企业,提供快速,高效,标准化,可定制,私有化部署的平台,在兼顾开发速度的同时,兼…...

C语言实现日本某地发生了一件谋杀案
题目 猜凶手 题目内容: 日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。 以下为4个嫌疑犯的供词: A说:不是我。 B说:是C。 C说:是D。 D说:C在胡说 已知3个人说了真话&…...
【C++】const成员
个人主页 : zxctscl 如有转载请先通知 文章目录 1. 前言2. const成员3. 取地址及const取地址操作符重载 1. 前言 在之前已经已经分享过了关于 【C】类和对象之常引用与运算符重载,这次分享的有关const的内容,话不多说,正文开始。…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

