KL divergence(KL 散度)详解
本文用一种浅显易懂的方式说明KL散度。
参考资料
KL散度本质上是比较两个分布的相似程度。
现在给出2个简单的离散分布,称为分布1和分布2.
分布1有3个样本,
其中A的概率为50%, B的概率为40%,C的概率为10%
分布2也有3个样本:
其中A的概率为50%,B的概率为10%,C的概率为40%。
现在想比较分布1和分布2的相似程度。
直观看上去分布1和分布2中样本A的概率是一样的,仅仅B和C的概率换了一下。
分布应该是相似的,但是如何量化来看呢。
可以这样做,用分布1的各个样本的概率和分布2样本概率做比值,相加再求平均。
现假设分布1的概率分布为P,分布2的概率分布为Q,
那么P(A) = 0.5, P(B)=0.4, P( C) = 0.1
Q(A) = 0.5, Q(B) = 0.1, Q( C) = 0.4,
各样本概率做比值之后为:
P(A)/Q(A) + P(B)/Q(B) + P( C)/Q( C) = 1+4+1/4
再对3个样本取平均: (1+4+1/4) / 3 = 1.75
这就是我们想要的分布1和分布2的相似度。
不过有一个问题,
可以看到P(B)和Q(B), P( C)和Q( C)仅仅概率做了交换,它们的相似度大小应该是一样的(仅仅方向不一样),
也就是说P(B)/Q(B), P( C)/Q( C)的绝对值应该是一样的,符号不一样。
但是现在,哪个分子大哪个结果就大,这是不应该的,
想要这样一个函数来解决这个问题,
f(4) = y
f(1/4) = -y,
这里的4为P(B)/Q(B), 1/4为P( C)/Q( C),
经过f(x)后得到的应该是同样的相似度大小,只是方向不一样,一个是变大的方向,一个是变小的方向,用负号表示方向的不同。
那么什么样的函数能满足f(x)呢,
可以取几个值画一下,你会发现,这个f(x)就是log(x)。
那么现在把刚才的相似度修改一下,
把简单的P(x)/Q(x)换成log(P(x) / Q(x)).
于是变为: ∑ 1 n l o g P ( x ) Q ( x ) / n \sum_{1}^{n} log\frac{P(x)}{Q(x)} / n 1∑nlogQ(x)P(x)/n
对样本取平均值表示每个样本的weight都是1/n,
不要取这么平均,把weight改为P(x),
那么就得到 ∑ 1 n P ( x ) l o g P ( x ) Q ( x ) \sum_{1}^{n} P(x) log\frac{P(x)}{Q(x)} 1∑nP(x)logQ(x)P(x)
这就是我们熟悉的KL散度,它比较的是分布P和分布Q的相似度。
“||”右边的Q表示是reference分布。
K L ( P ∣ ∣ Q ) = ∑ 1 n P ( x ) l o g P ( x ) Q ( x ) KL(P||Q) = \sum_{1}^{n} P(x) log\frac{P(x)}{Q(x)} KL(P∣∣Q)=1∑nP(x)logQ(x)P(x)
相关文章:
详解)
KL divergence(KL 散度)详解
本文用一种浅显易懂的方式说明KL散度。 参考资料 KL散度本质上是比较两个分布的相似程度。 现在给出2个简单的离散分布,称为分布1和分布2. 分布1有3个样本, 其中A的概率为50%, B的概率为40%,C的概率为10% 分布2也有3个样本: 其…...

AzerothCore@FreeBSD安装记录
尝试在FreeBSD系统下安装AzerothCore 首先安装相关软件 pkg install cmake mysql80-server boost-all装完mysql之后提示: MySQL80 has a default /usr/local/etc/mysql/my.cnf, remember to replace it with your own or set mysql_optfile"$YOUR_CNF_FILE i…...

vue .env配置环境变量
最近使用的不同的环境有点多了,接口文件ip一直在替换打包,看了下文档,有个方案使用.env配置不同的环境运行打包 vue 现在已经兼容了env ,无需下载 创建文件(根目录) 创建.env.development,.env.…...

ThreadLocal介绍
文章目录 ThreadLocal源码分析:set方法get方法remove方法 ThreadLocal内存泄漏问题 ThreadLocal ThreadLocal提供了线程局部变量,每个线程都可以通过set和get方法来对这个变量进行操作,但不会和其他线程的局部变量冲突,实现了线程…...
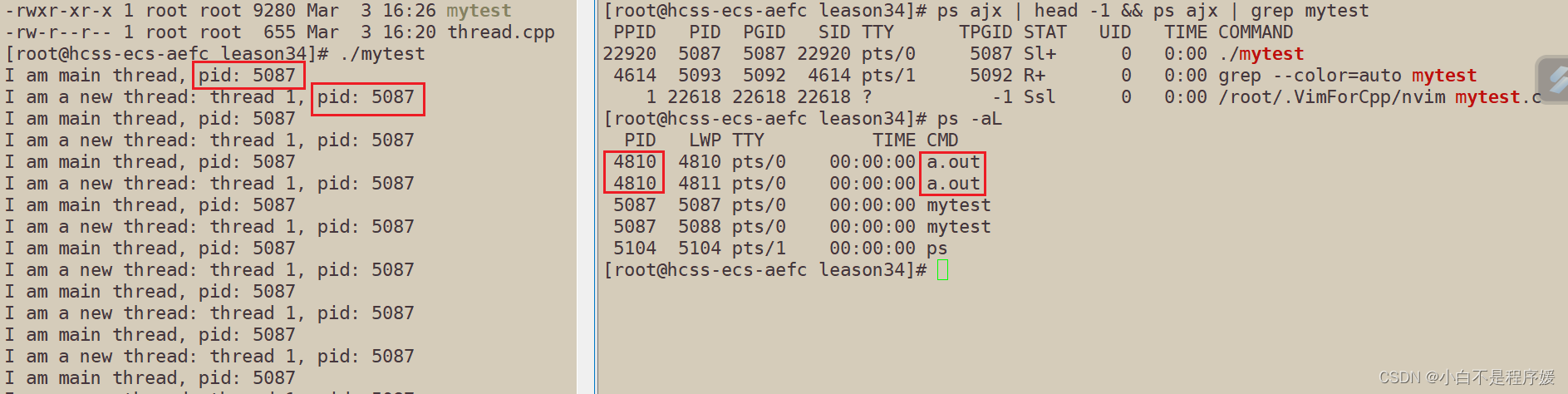
【Linux系统化学习】线程概念
目录 线程的概念 线程的引出 什么是线程 理解线程比进程更加的轻量化 线程的优点 现成的缺点 线程异常 线程用途 Linux进程VS线程 线程的简单现象 线程的概念 有关操作系统的书籍或者课本都会这样描述线程: 线程是比进程轻量化的一种执行流线程是进程内部…...

Redis集群模式
分片 面试题:为什么Redis的最大槽位是16384? 翻译一下作者的话: 解读一下:...

执行go get xxx报错
1、执行命令 go get github.com/go-redis/redis/v8 报错 : go: coding.jd.com/xxx/xxxxxxv0.0.0-xxxxxxxxxx: invalid version: git ls-remote -q origin in /users/douhao7/go/pkg/mod/cache/vcs/xxxxxxxxxxxxxx: exit status 128: 致命错误:could not read use…...

MATLAB基础语法与实践
文章目录 初级篇MATLAB简介特点 安装和配置界面介绍 中级篇基础语法变量表达式函数 数据类型整数和浮点数复数字符串单元数组 高级篇脚本与函数编写脚本编写函数编写 图形绘制数据分析 实践篇实例演示1:矩阵运算实例演示2:数据可视化 初级篇 MATLAB简介…...
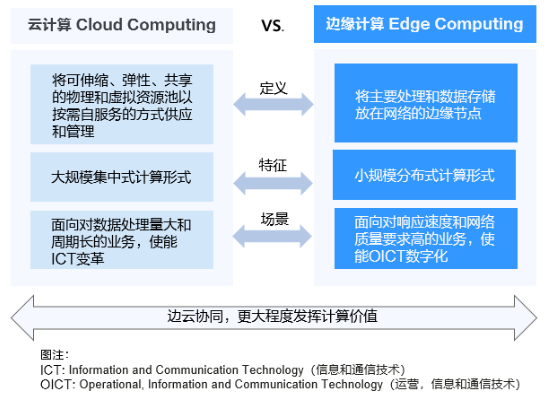
智能边缘小站 CloudPond(低延迟、高带宽和更好的数据隐私保护)
智能边缘小站 CloudPond(低延迟、高带宽和更好的数据隐私保护) 边缘小站的主要功能是管理用户在线下部署的整机柜设施,一个边缘小站关联一个华为云指定的区域和一个用户指定的场地,相关的资源运行状况监控等。 边缘计算 迈入5G和AI时代,新…...
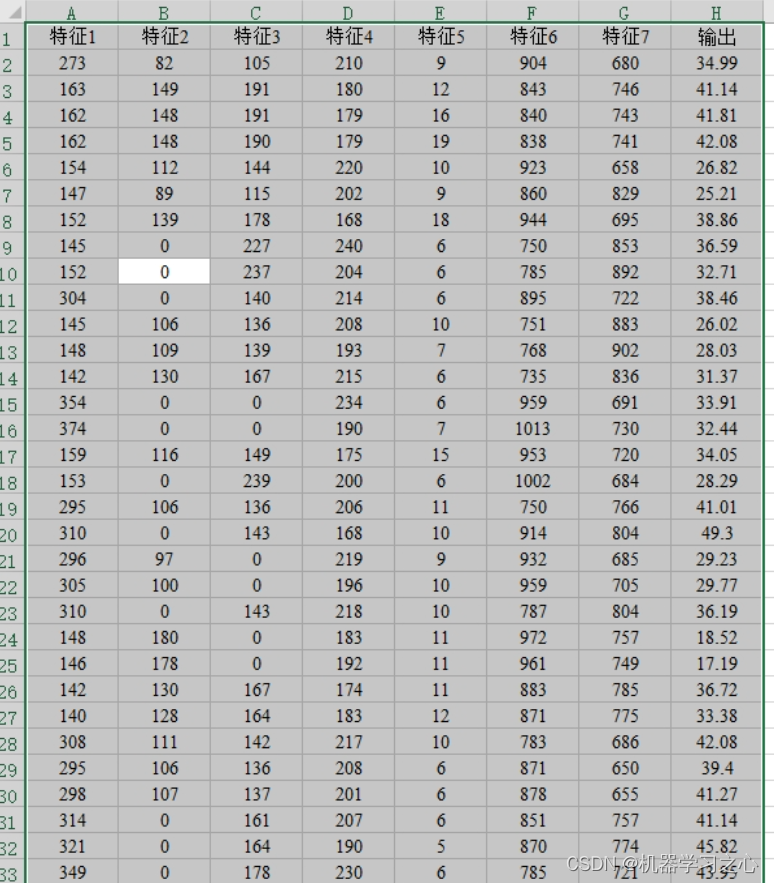
回归预测 | Matlab实现RIME-BP霜冰算法优化BP神经网络多变量回归预测
回归预测 | Matlab实现RIME-BP霜冰算法优化BP神经网络多变量回归预测 目录 回归预测 | Matlab实现RIME-BP霜冰算法优化BP神经网络多变量回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab实现RIME-BP霜冰算法优化BP神经网络多变量回归预测(完整…...

LeetCode15:三数之和
题目描述 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组…...
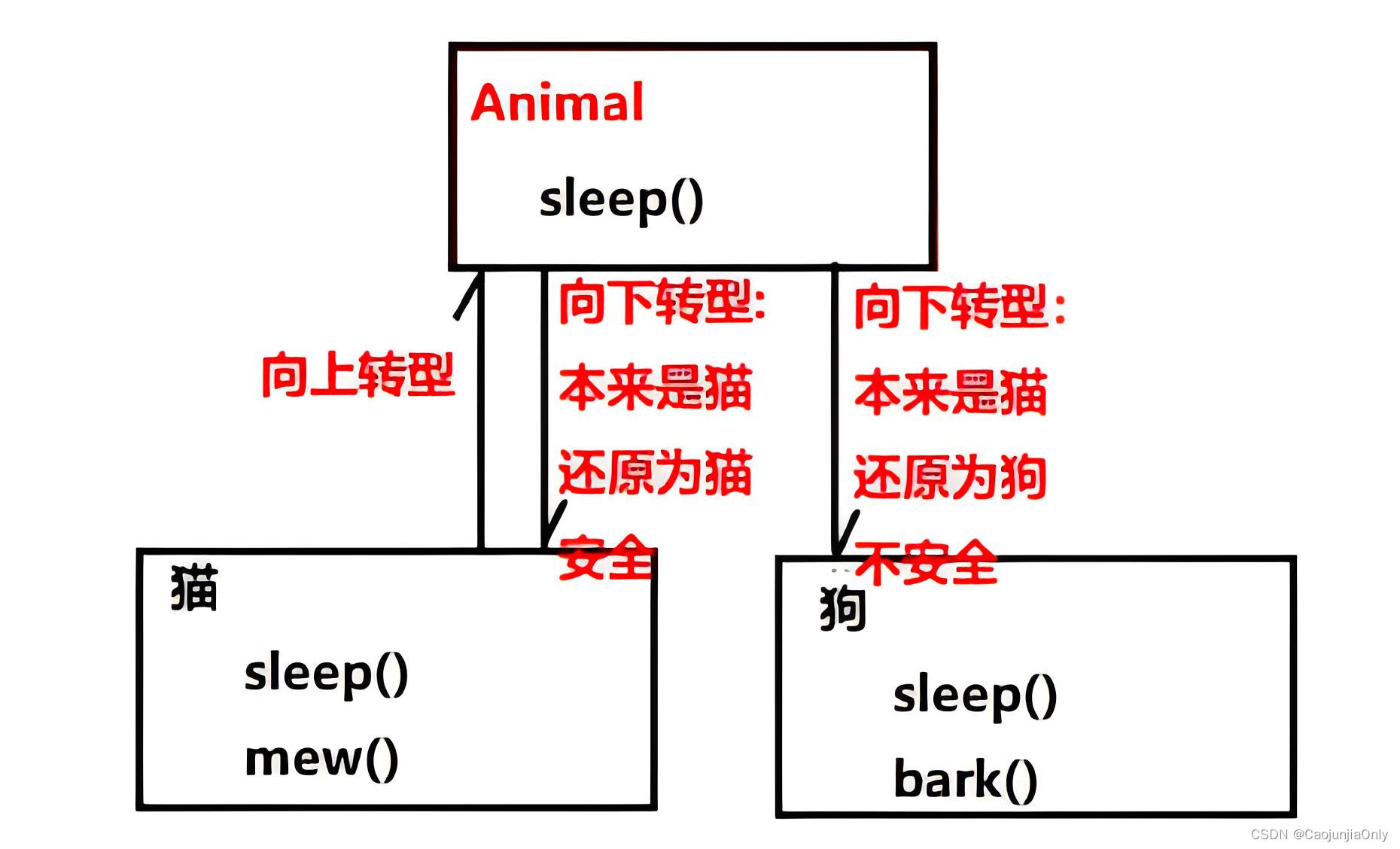
【详识JAVA语言】面向对象程序三大特性之三:多态
多态 多态的概念 多态的概念:通俗来说,就是多种形态,具体点就是去完成某个行为,当不同的对象去完成时会产生出不同的状态。 多态实现条件 在java中要实现多态,必须要满足如下几个条件,缺一不可…...
nginx(三)实现反向代理客户端 IP透传
正常情况下,客户端去访问代理服务器,然后代理服务器再取访问真实服务器,在真实服务器上,只能显示代理服务器的ip地址,而不显示客户端的ip地址,如果想让客户端的ip地址也能在真实服务端看见,这一…...

深入Java日志框架及其最佳实践
概述 在Java应用开发中,日志框架是确保应用稳定性和可观察性的关键组件。它帮助开发者记录应用的行为、诊断问题,并监控系统的健康状况。随着Java生态系统的不断发展,各种日志框架也应运而生,各有特点和优势。本文将详细探讨几个…...

threejs显示本地硬盘上的ply文件,通过webapi
由于ply文件是第三方提供的,threejs无法用绝路路径的方式显示ply 所以想通过webapi把ply通过url地址的方式给threejs 1.webapi部分 /// <summary>/// 获取PLY文件/// </summary>/// <returns></returns>[HttpPost(Name "GetPly&qu…...
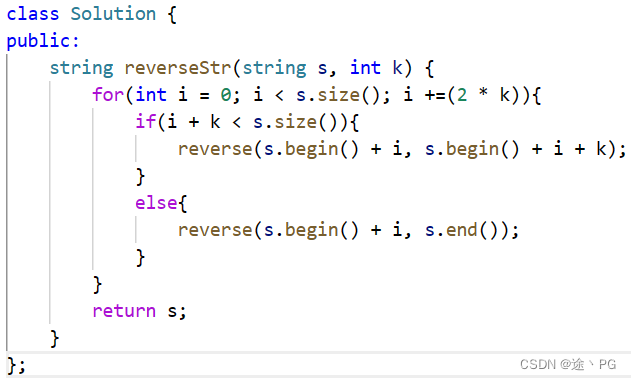
代码随想录day10(2)字符串:反转字符串Ⅱ (leetcode541)
题目要求:给定一个字符串 s 和一个整数 k,从字符串开头算起, 每计数至 2k 个字符,就反转这 2k 个字符中的前 k 个字符。如果剩余字符少于 k 个,则将剩余字符全部反转。如果剩余字符小于 2k 但大于或等于 k 个,则反转前…...

【MySQL】_联合查询基础表
联合查询也称为多表查询,是将多个表联合到一起进行查询; 笛卡尔积是联合查询的基础,笛卡尔积其实就是一种排列组合,把两张表的记录尽可能地排列组合出n种情况: 以两张表:班级表与学生表为例,计…...
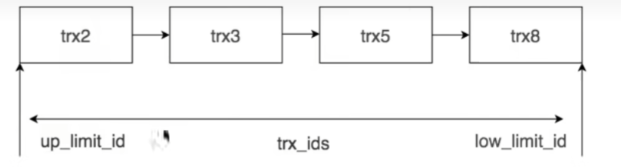
InnoDB存储引擎对MVCC的实现
MVCC MVCC的目的 在搞清楚MVCC之前,我们要搞懂一个问题,MVCC到底解决的是什么问题? 我用一句话概括,那就是为了解决读-写可以一起的问题! 在我们的印象里,InnoDB可以读读并发,不能读写并发,或者写写并发 这是很正常的想法,因为如果读写并发的化,会有并发问题 而对于写写…...

【精选】Java项目介绍和界面搭建——拼图小游戏 中
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏 …...

C++ //练习 10.16 使用lambda编写你自己版本的biggies。
C Primer(第5版) 练习 10.16 练习 10.16 使用lambda编写你自己版本的biggies。 环境:Linux Ubuntu(云服务器) 工具:vim 代码块 /*******************************************************************…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
