PID闭环控制算法的学习与简单使用
平台:matlab2021b,Vivado2018
应用场景和理解
一个早餐店,假如一天都有生意,生意有的时间很火爆,有时候又一般,老板又是个实在人,只知道在后厨蒸包子。由于包子蒸熟需要一定的时间,老板娘在前面卖包子。老板娘耍了一会儿手机,客人买包子的速度很快,一会儿包子就卖完了,老板娘给老板说包子卖完了。老板说马上包。这个问题就可以使用我们的公式来控制,老板娘如果不耍手机,隔几分钟就告诉老板现在还有多少包子。老板根据现在的情况来包包子,保证整体的数量恒定。根据这个例子来说明PID的含义,老板娘看剩余包子个数的频率为几分钟一次还是十几分钟一次。这个时间就是采样时间T。老板加包子有时候抱一笼出来,有时候抱几笼出来,一次拿一笼出来赶不上客人吃包子的速度,一次拿几笼出来,发现客人吃的慢,很久都不用拿出来。这个拿包子的笼数就是比例系数P。在加包子的过程中,有时候直接把蒸笼拿上去蒸,导致累的过高,老板娘取不下来。这时候把包子放在这里,让老板娘自己去把蒸笼放好。这里老板娘控制的放的方式就是积分时间I。后面有时候客人一次买很多包子,有些客人就买几个,老板有时候抱出来的包子太多了,有时候又抱出来的太少了,老板自己想了个办法,在半路上老板娘在看一眼,发现抱多了,就放一些回去,拿少了就再去抱一些出来。这个多少就是微分时间D。好了现在经过一系列的操作老板终于可以保证外面的包子稳定在一个恒定的个数上了。
算法公式
PID控制算法是一种闭环控制算法。在工业中被广泛应用。在PID系统框图中,整个系统包括比较器、PID控制器和控制对象,其中PID控制器包括三个模块,比例(P),积分(I)和微分(D)。

r(t)为系统的目标值,y(t)为系统的输出值。e(t)为系统目标值和输出值的偏差。
u(t)作为控制系统中的中间变量,既是偏差e(t)通过PID控制算法处理后的输出量。又是被控制对象的输入量。因此模拟PID控制器的公式为:
其中,为比例增益,
为积分时间常数,
为微分时间常数。
PID离散化算法公式
离散化的算法公式分为位置式PID算法和增量式算法。
位置式算法,假设采样时间间隔为T,则在k时刻:偏差为e(k);积分为e(k),e(k-1),e(k-2)…+e(0);微分时间为(e(k)-e(k-1))/T。离散化后的公式为
上式化简为
增量式PID算法
根据位置式可知
则
可以得出
以上就是增量式算法,由增量式算法公式可知,系统的增量只和进三次偏差有关系。
由上述公式特点可以分析出来。位置式公式,需要多每次的误差进行累加,每次的输出都和过去的状态有关系。而增量式公式,误差只与最近三次采集有关系。但是积分影响大,稳态误差。
下面我们将通过matlab仿真对该公式进行分析,详细分析两种公式的参数影响。
先看位置式PID
clc;
clear;PID_target = 24; % 目标温度为24摄氏度% 定义PID三个参数的初始值
Kp = 0.01;
Ki = 0;
Kd = 0;% 定义误差
ek = 0;
ek_1 = 0;
ek_sum = 0;
sum_threshold = 8; % 阈值设定为8% PID输出
PID_out = 0;% 数据采集点数
numPoints = 200;% 采集初始值
ADC_data = zeros(1,numPoints);% 存储PID输出数据
PID_out_data = zeros(1, numPoints);
PID_target_data = PID_target * ones(1, numPoints);% 计算PID输出
for t = 4:numPointsek = PID_target - ADC_data(t-3);if (t>=12)ek_sum = ek_sum - ek_sum/sum_threshold;endek_sum = ek_sum+ek;PID_out = PID_out + Kp * ek + Ki * ek_sum + Kd * (ek - ek_1);ek_1 = ek;
% ADC_data(t) = PID_out + randn(1); % 添加随机噪声ADC_data(t) = PID_out; PID_out_data(t) = PID_out;
end% 绘制PID_out和PID_target的图像
figure;
hold on;
plot(1:numPoints, PID_out_data, 'b', 'LineWidth', 1.5);
plot(1:numPoints, PID_target_data, 'r--', 'LineWidth', 1.5);
hold off;
title('PID输出与目标值变化图像');
xlabel('时间步数');
ylabel('数值');
legend('PID输出', '目标值', 'Location', 'best');在应用过程中对误差累积求和往往往往不需要进行全部累加。这里代码中只累加了8次。采集值我这里做了延迟响应,即PID调整三个值后在响应第一个点。这样就模拟了外部的响应时间。这里我们将调节目标设置在10个点左右到达稳定值。
设置初始值P=0.01;I=0;D=0;

调节时间明显过长。
设置值P=0.1;I=0;D=0;

缩短了调节时间但是不够。
设置值P=0.2;I=0;D=0;
 调节时间满足了但是有点过冲了。这里看一下积分项I的作用,稍微增大一点点。
调节时间满足了但是有点过冲了。这里看一下积分项I的作用,稍微增大一点点。
设置值P=0.2;I=0.005;D=0;

可以看到过冲更加明显了。
设置值P=0.2;I=0.005;D=0.01;

尝试使用微分将过冲调节下来。适当增大微分项。
设置值P=0.2;I=0.005;D=0.2;

减小了一点点。但是减不下去。
设置值P=0.2;I=0.0005;D=0.2;在减少积分项将过冲拉低。

可以看到波形过冲消失,但是不够平滑。
适当的缩小I微分参数,可以将波形调整到很平滑的位置。差不多达到我们预计的要求。
设置值P=0.2;I=0.0005;D=0.1;

再看增量式PID
clc;
clear;PID_target = 24; % 目标温度为24摄氏度% 定义PID三个参数的初始值
Kp = 0.01;
Ki = 0.01;
Kd = 0.01;% 定义误差
ek = 0;
ek_1 = 0;
ek_2 = 0;% PID输出
PID_out = 0;% 采集初始值
ADC_data = 0;% 数据采集点数
numPoints = 200;% 采集初始值
ADC_data = zeros(1,numPoints);% 存储PID输出数据
PID_out_data = zeros(1, numPoints);
PID_target_data = PID_target * ones(1, numPoints);% 计算PID输出
for t = 4:numPointsek = PID_target - ADC_data(t-3);PID_out = PID_out + Kp * (ek - ek_1) + Ki * ek + Kd * (ek - 2 * ek_1 + ek_2);ek_2 = ek_1;ek_1 = ek;
% ADC_data(t) = PID_out + randn(1); % 添加随机噪声ADC_data(t) = PID_out ; % 添加随机噪声PID_out_data(t) = PID_out;
end% 绘制PID_out和PID_target的图像
figure;
hold on;
plot(1:numPoints, PID_out_data, 'b', 'LineWidth', 1.5);
plot(1:numPoints, PID_target_data, 'r--', 'LineWidth', 1.5);
hold off;
title('PID输出与目标值变化图像');
xlabel('时间步数');
ylabel('数值');
legend('PID输出', '目标值', 'Location', 'best');设置初始值
设置初始值P=0.01;I=0.01;D=0.01;

适当增加比例系数P=0.2;I=0.01;D=0.01;

波形调节无明显变化。前面说到增量式积分项对响应时间影响较大,这里适当增加积分项。
P=0.2;I=0.1;D=0.01;

继续增加积分项到满足调节时间P=0.2;I=0.26;D=0.01;

满足了调节时间有了过冲,适当P=0.2;I=0.26;D=0.1;

可以看到波形在接近目标值的时候震荡。继续调整参数。发现要到达预定的响应时间,波形不会平滑。笔者又尝试了一些参数。
最后P=0.01;I=0.17;D=0.01;波形接近稳定,但是没有达到预计的响应时间。
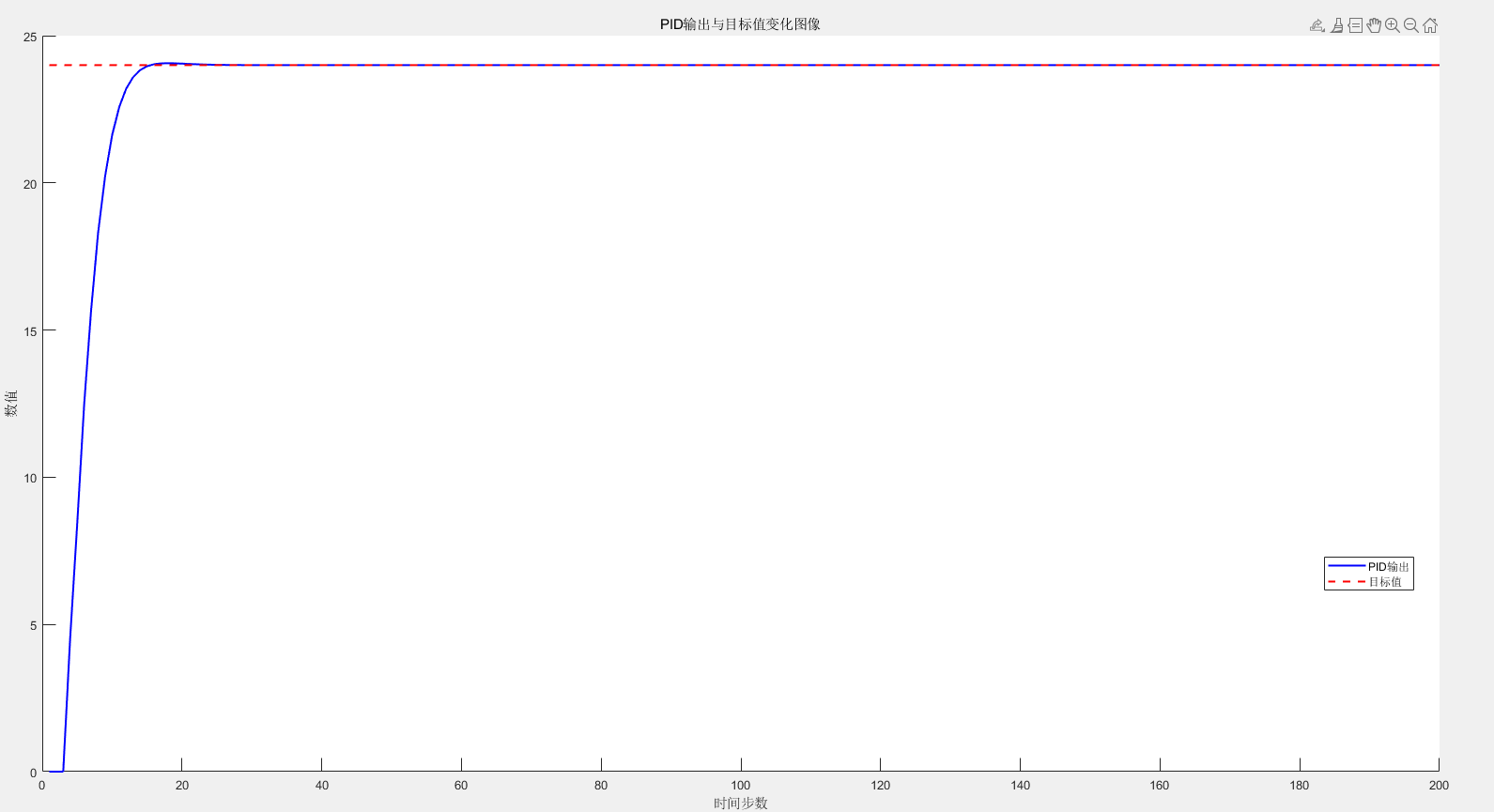
从上面可以看出来位置式相对增量式可以更快更稳定的达到响应时间。且位置式的参数的作用和增量式参数的作用在调试的过程中有一点点差别。从实现方式来看,增量式的计算量明显更小。
参考
演示PID三个参数的控制作用 (qq.com)
相关文章:

PID闭环控制算法的学习与简单使用
平台:matlab2021b,Vivado2018 应用场景和理解 一个早餐店,假如一天都有生意,生意有的时间很火爆,有时候又一般,老板又是个实在人,只知道在后厨蒸包子。由于包子蒸熟需要一定的时间,老…...
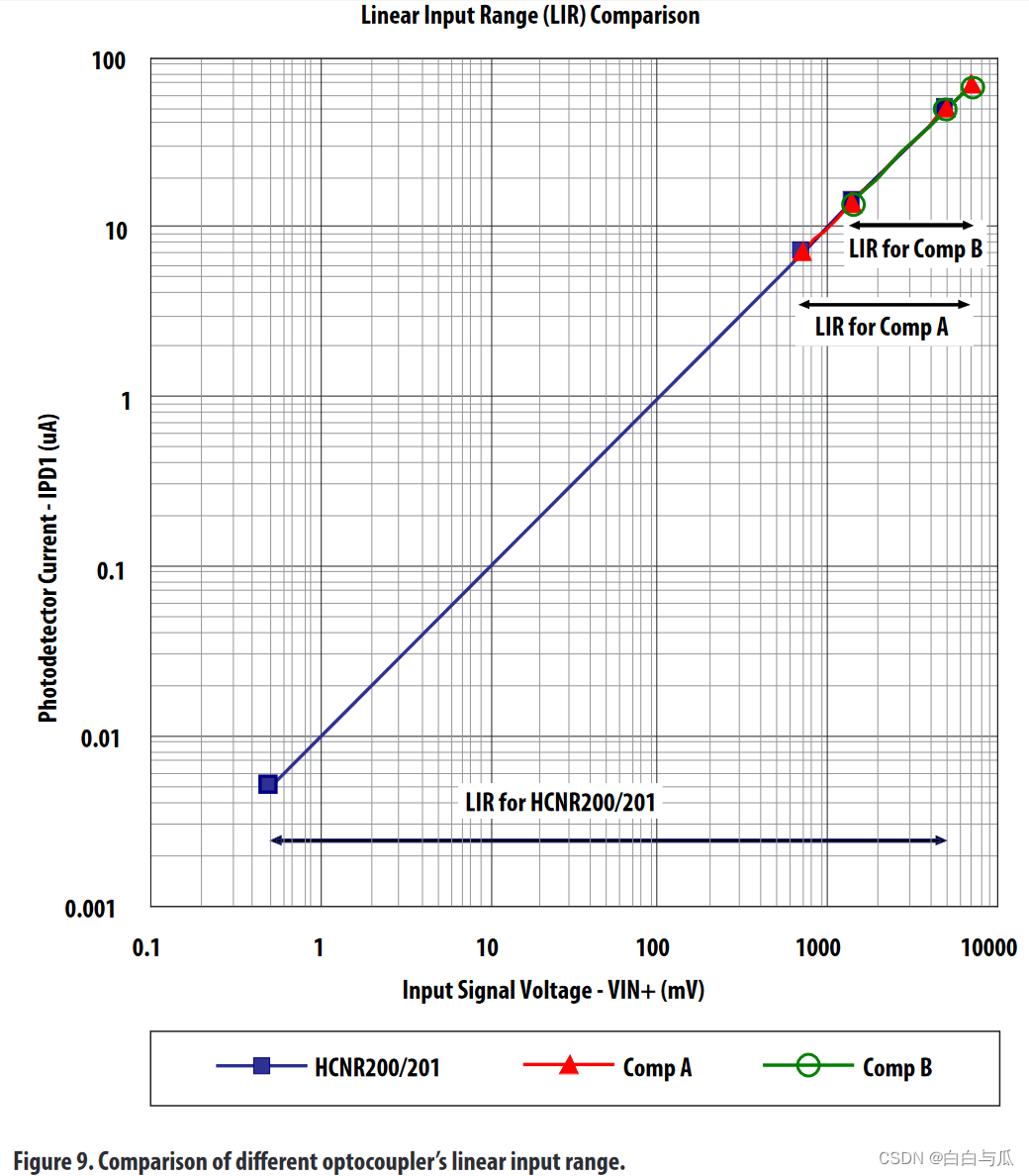
【无刷电机学习】光耦HCNR200基本原理及应用(资料摘抄)
【仅作自学记录,不出于任何商业目的。如有侵权,请联系删除,谢谢!】 本文摘抄翻译自: https://docs.broadcom.com/wcs-public/products/application-notes/application-note/331/6/av02-1333en-an_5394-16jul10.pdfhtt…...

【LeetCode】1768_交替合并字符串_C
题目描述 给你两个字符串 word1 和 word2 。请你从 word1 开始,通过交替添加字母来合并字符串。如果一个字符串比另一个字符串长,就将多出来的字母追加到合并后字符串的末尾。 返回 合并后的字符串 。 https://leetcode.cn/problems/merge-strings-al…...

C#解析JSON
https://blog.csdn.net/weixin_43046974/article/details/131449900 C#解析JSON 1. JSON定义2. JSON一般构成及解析方法3. 解析举例子 1. JSON对象解析,只包含一层对象{}2. 嵌套JSON对象解析,包含多层对象{}3. JSON数组解析1(数组循环遍历&…...

AI图像识别算法助力安全生产*提升风险监测效率---豌豆云
2024年开年来安全生产事故频发,工厂爆炸、工程坍陷等重大安全生产事故的发生再次为我们敲响了警钟。 安全生产是企业发展的生命线,而传统的安全监测手段存在盲区和延迟,难以及时发现和应对潜在风险。 AI图像识别算法通过利用先进的计算机视…...

CSS技巧:实现两个div在同一行显示的方法
css如何让两个div在同一行显示 - web开发 - 亿速云 在Web开发中,经常遇到需要将多个元素水平排列在同一行的情况。其中一个常见的需求是将两个div元素放置在同一行上,使它们并排显示。在本文中,我们将介绍几种实现这一效果的CSS方法。 1. 使…...
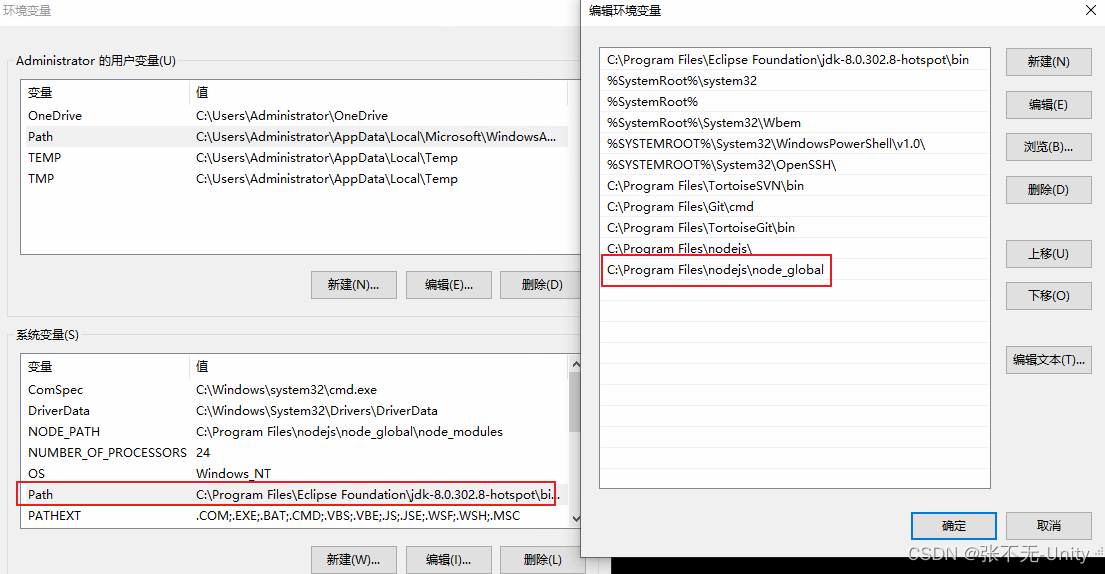
【Unity】Node.js安装与配置环境
引言 我们在使用unity开发的时候,有时候会使用一些辅助工具。 Node.js就是开发中,经常会遇到的一款软件。 1.下载Node.js 下载地址:https://nodejs.org/en 2.安装Node.js ①点击直接点击Next下一步 ②把协议勾上,继续点击…...

Vue3:使用 Composition API 不需要 Pinia
在 Vue.js 开发的动态环境中,在单个组件中处理复杂的业务逻辑可能会导致笨重的文件和维护噩梦。虽然 Pinia 提供集中式状态管理,但仅依赖它来处理复杂的业务逻辑可能会导致代码混乱。本文探讨了使用 Composition API 的替代方法,说明开发人员…...

ExoPlayer 播放视频黑屏的解决方法
最近项目中在使用 ExoPlayer 来进行视频的播放,开发过程中遇到了部分视频打开后黑屏的问题,报错日志如下。 E Audio codec error android.media.MediaCodec$CodecException: Error 0xe E Playback error androidx.media3.exoplayer.ExoPlaybackExcept…...
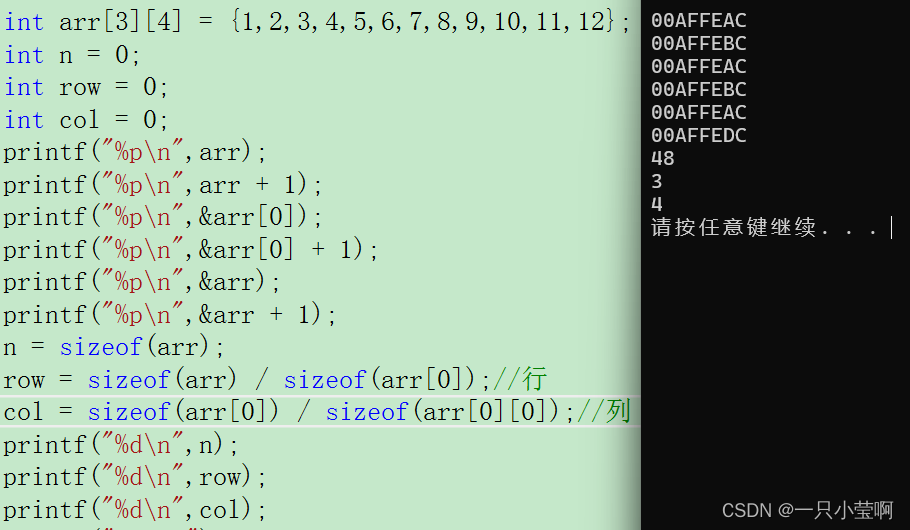
C语言初阶—数组
数组是一组相同类型元素的集合。 在C99标准之前,数组的大小必须是常量或常量表达式。 在C99标准之后,数组的大小可以是变量,可以支持变长数组,但变长数组不能初始化。 不完全初始化,剩余的元素默认初始化为0 。 数组访…...
数据预处理教程)
飞桨(PaddlePaddle)数据预处理教程
文章目录 飞桨(PaddlePaddle)数据预处理教程1. 安装飞桨2. 了解飞桨的数据预处理方法3. 应用单个数据预处理方法4. 组合多个数据预处理方法5. 在数据集中应用数据预处理5.1 在框架内置数据集中应用5.2 在自定义数据集中应用 6. 总结 飞桨(Pad…...
MYSQL C++链接接口编程
使用MYSQL 提供的C接口来访问数据库,官网比较零碎,又不想全部精读一下,百度CSDN都是乱七八糟的,大部分不可用 官网教程地址 https://dev.mysql.com/doc/connector-cpp/1.1/en/connector-cpp-examples-connecting.html 网上之所以乱七八糟,主要是MYSQL提供了3个接口两个包,使用…...

并发编程中常见的设计模式,c++多线程如何设计
C多线程设计(任务的“多对一”、“一对多”、“多对多”情况 该如何设计线程?) C书籍中并未找到对多线程设计,有很完整详细的总结!!C并发编程书籍中也只是一些理论或则零散的多线程实例。无奈,…...
解决android studio build Output中文乱码
1.效果如下所示: 代码运行报错的时候,Build Output报的错误日志中中文部分出现乱码,导致看不到到底报的什么错。 2.解决办法如下: 点击Android studio开发工具栏的Help-Edit Custom VM Options....,Android studio会…...
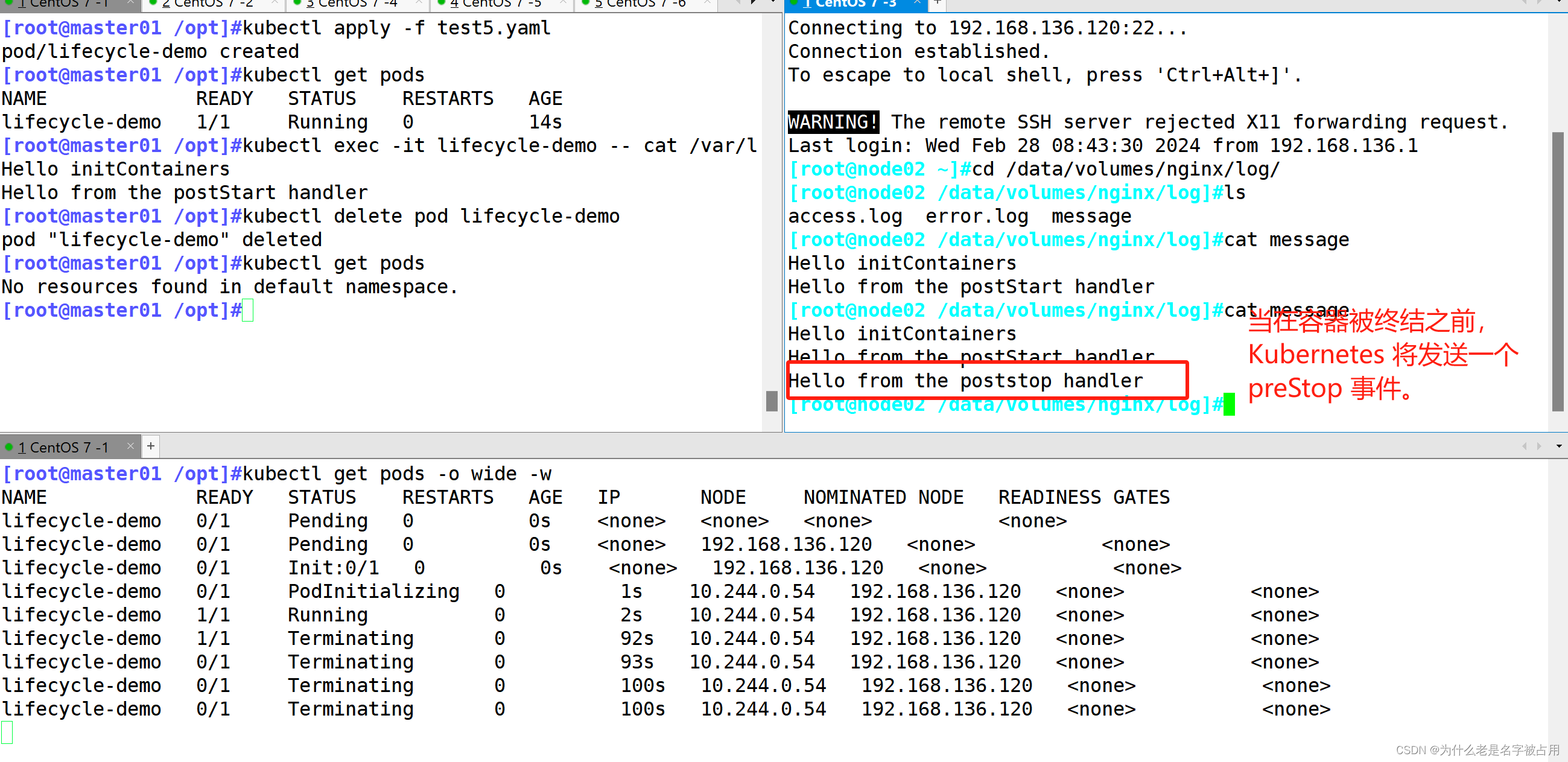
[云原生] K8s之pod进阶
一、pod的状态说明 (1)Pod 一直处于Pending状态 Pending状态意味着Pod的YAML文件已经提交给Kubernetes,API对象已经被创建并保存在Etcd当中。但是,这个Pod里有些容器因为某种原因而不能被顺利创建。比如,调度不成功(…...
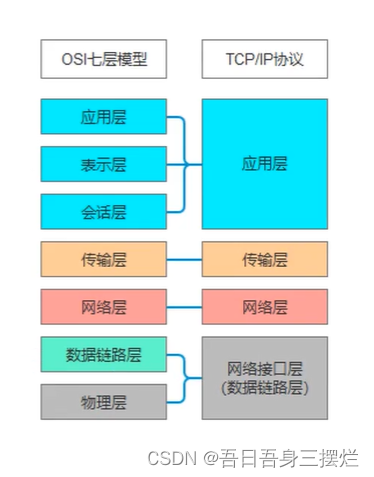
[Unity3d] 网络开发基础【个人复习笔记/有不足之处欢迎斧正/侵删】
TCP/IP TCP/IP协议是一 系列规则(协议)的统称,他们定义了消息在网络间进行传输的规则 是供已连接互联网的设备进行通信的通信规则 OSI模型只是一个基本概念,而TCP/IP协议是基于这个概念的具体实现 TCP和UDP协议 TCP:传输控制协议,面向连接,…...

Tomcat的配置文件
Tomcat的配置文件详解 一.Tomcat的配置文件 Tomcat的配置文件默认存放在$CATALINA_HOME/conf目录中,主要有以下几个: 1.server.xml: Tomcat的主配置文件,包含Service, Connector, Engine, Realm, Valve, Hosts主组件的相关配置信息&#x…...

猴子吃桃问题(python版)
文章预览: 题目python解法一:运行结果 python解法二:运行结果 python解法三:运行结果 题目 猴子吃桃问题:猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。 第二天早…...
的整数值,每读取一个值,程序打印出该值个数的 *。)
C语言入门到精通之练习49:读取7个数(1—50)的整数值,每读取一个值,程序打印出该值个数的 *。
题目:读取7个数(1—50)的整数值,每读取一个值,程序打印出该值个数的 *。 程序分析:无。 实例 #include<stdio.h> #include<stdlib.h> int main() {int n,i,j;printf("请输入…...

如何在Windows轻量应用服务器上安装和配置SSH?
如何在Windows轻量应用服务器上安装和配置SSH? 检查OpenSSH的可用性:首先,需要以管理员身份打开PowerShell并运行命令Get-WindowsCapability - Online | Where-Object Name - like OpenSSH*来检查OpenSSH服务是否可用。如果服务未启动或不可…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
