牛客练习赛122
D:圆
正着求删除的最小代价不好做,采用逆向思维,求选择一些不相交的线段使得构成一个圆的代价尽量大,最后答案就是所有线段权值之和减去最大代价。
那么如何求这个最大代价呢?显然区间DP
老套路:破环成链,枚举区间长度 len ,枚举区间左端点 i 和右端点 j
很明显没有线段长度为1,故len从2开始
具体的
线段的操作和点的相似但又不完全相同具体看代码即可。
1:不选择以左端点的线段,
2、选择以为左端点的线段。枚举左端点 所能到达的右端点 v,权值为 w,那么当前的答案
由 区间 的答案加上 区间
的答案加上线段
的权值构成,即
int n, m;
int f[M][M]; // f[i][j] 区间i到j不相交边的最大价值
vector<PII> g[N];
void solve()
{cin >> n >> m;int s = 0;for (int i = 1; i <= m; i++){int x, y, w;cin >> x >> y >> w;if (x > y)swap(x, y);g[x].pb({y, w});g[y].pb({x + n, w});s += w;}for (int len = 2; len <= 2 * n; len++){for (int i = 1; i + len - 1 <= 2 * n; i++){int j = i + len - 1;f[i][j] = f[i + 1][j]; // 不选择以i为左端点的线段for (auto ed : g[i]) // 选择以i为左端点的线段{int v = ed.xx, w = ed.yy;if (v > j) // 已经越过右端点了continue;if (v - 1 > i + 1) //区间端点,不能相同w += f[i + 1][v - 1];if (j > v + 1)w += f[v + 1][j];f[i][j] = max(f[i][j], w);}}}int tmp = 0;for (int i = 1; i <= n; i++)tmp = max(tmp, f[i][i + n - 1]);s = s - tmp;cout << s << endl;
}类似的题目
Codeforces Round 661 (Div. 3)
F. Yet Another Segments Subset
两个题目非常相似但是又不完全相同。
本题的数据显然如果直接区间dp会超时,但是n却是很小我们想能不能进行离散化。
本题的相交比较上一题有点不同,不同在包含的时候端点可以相交,而不包含时端点不可相交。
很明显,离散化候不同区间值被拉近了距离,但是不相交得还是不相交,所以本题可以离散化。(具体题目具体分析,有的题目可能会有坑)
状态表示: 表示区间
里面满足题意得最大区间数量。
然后我们就想一下转移方程:
具体的还是区间DP的过程,枚举区间长度 len ,枚举区间左端点 i 和右端点 j
我们还是以选不选以 为左端点的区间,
1:不选
2:选
我们看第二个方程,很明显就是我们上面说的;
即只有完全包含端点才可以相同;
我们还要注意一种情况那就是区间恰好等于 ,这种情况由于
,被跳过了
所以最后加上个数即可完成。
int n;
PII p[N];
vector<int> g[N];
void solve()
{vector<int> t;cin >> n;for (int i = 1; i <= n; i++){int l, r;cin >> l >> r;p[i] = {l, r};t.pb(l);t.pb(r);}sort(t.begin(), t.end());t.erase(unique(t.begin(), t.end()), t.end());for (int i = 1; i <= n; i++){int x = lower_bound(t.begin(), t.end(), p[i].xx) - t.begin() + 1;int y = lower_bound(t.begin(), t.end(), p[i].yy) - t.begin() + 1;g[x].pb(y);}int m = t.size();vector<vector<int>> f(m + 10, vector<int>(m + 10));for (int len = 1; len <= m; len++){for (int i = 1; i + len - 1 <= m; i++){int j = i + len - 1;f[i][j] = f[i + 1][j];int cnt = 0;for (auto ed : g[i]){int v = ed;if (v == j)cnt++;if (v < j)f[i][j] = max(f[i][v] + f[v + 1][j], f[i][j]);}f[i][j] += cnt;}}cout << f[1][m] << endl;for (int i = 0; i <= m + 1; i++)g[i].clear();
}相关文章:
牛客练习赛122
D:圆 正着求删除的最小代价不好做,采用逆向思维,求选择一些不相交的线段使得构成一个圆的代价尽量大,最后答案就是所有线段权值之和减去最大代价。 那么如何求这个最大代价呢?显然区间DP 老套路:破环成链࿰…...
软考复习调整策略和学习计划!
根据软考办发布的最新通知,在群里引起了热烈讨论的是2024年度计算机技术与软件专业技术资格(水平)考试的安排。其中,信息系统项目管理师(简称高项)的考试次数从每年两次减少到只有5月份进行,而系…...

1小时网络安全事件报告要求,持安零信任如何帮助用户应急响应?
12月8日,国家网信办起草发布了《网络安全事件报告管理办法(征求意见稿)》(以下简称“办法”)。拟规定运营者在发生网络安全事件时应当及时启动应急预案进行处置。 1小时报告 按照《网络安全事件分级指南》,…...

mysql使用连接池
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、mysql连接池?二、使用步骤1.引入库 前言 提示:这里可以添加本文要记录的大概内容: 例如: 提示:…...

06. Nginx进阶-Nginx代理服务
proxy代理功能 正向代理 什么是正向代理? 正向代理(forward proxy),一个位于客户端和原始服务器之间的服务器。 工作原理 为了从原始服务器获取内容,客户端向代理发送一个请求并指定目标(即原始服务器…...

STM32 (1)
1.基本信息 stm32是由ST公司生产的一种32位微控制器(单片机)。 1.1 各种型号 stm32是32位单片机的总称,有多种不同的系列。 32即用32个比特位表示一个地址,寻址范围:0x00000000 --0xffffffff (4GB) 1.2 存储密度 …...
Spring初始(相关基础知识和概述)
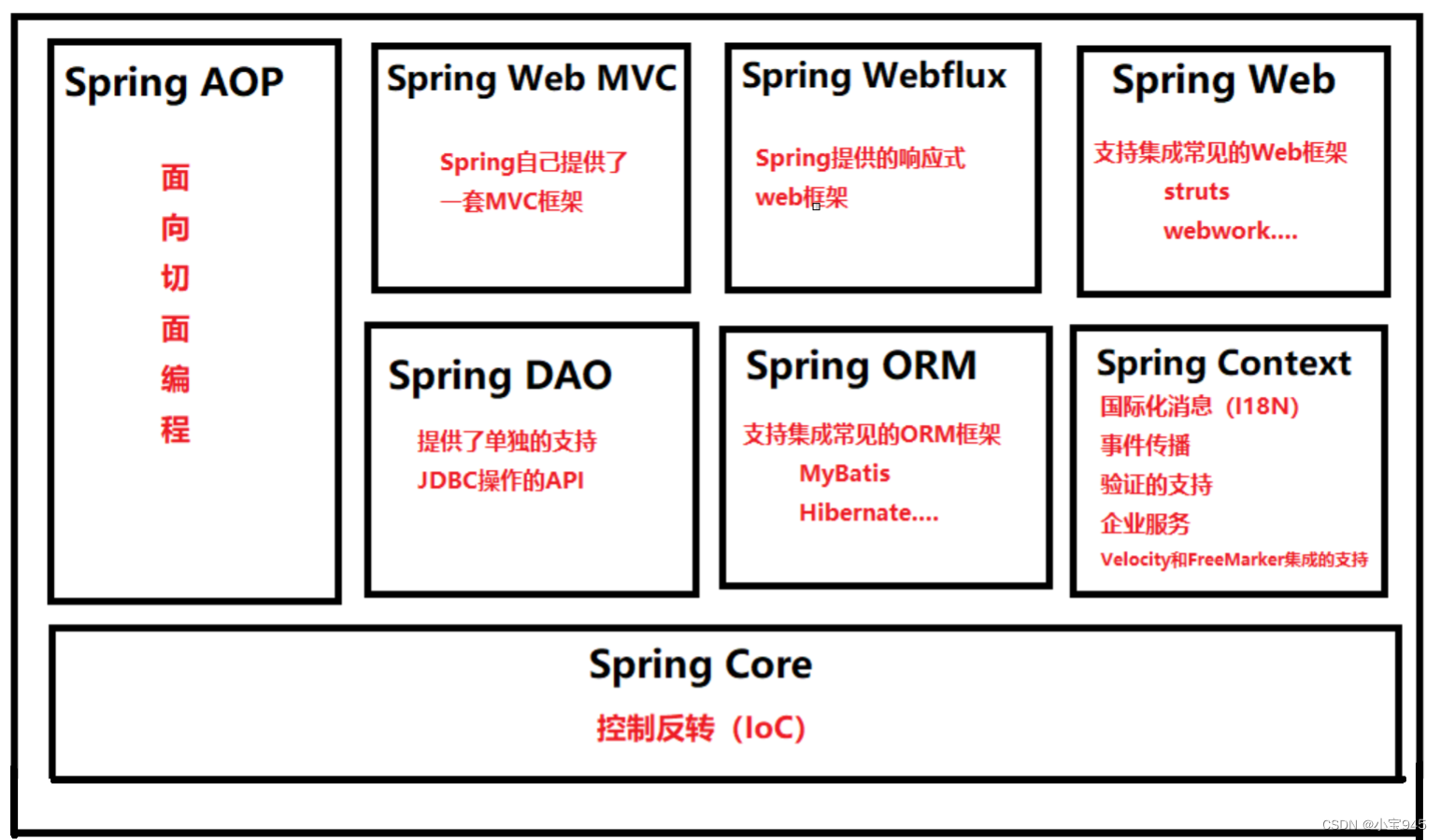
Spring初始(相关基础知识和概述) 一、Spring相关基础知识(引入Spring)1.开闭原则OCP2.依赖倒置原则DIP3.控制反转IoC 二、Spring概述1.Spring 8大模块2.Spring特点2.Spring的常用jar文件 一、Spring相关基础知识(引入S…...

【Swift 周报 第四十七期
文章目录 前言新闻和社区苹果财报来袭:营收有望再创新高 巴克莱或将惨遭打脸?Apple 为在全球范围内提供迷你 App 和游戏访问的流媒体游戏服务和 App 发布新选项Swift Student Challenge 将于 2 月 5 日开放申请 提案通过的提案正在审查的提案 Swift论坛推…...

STM32(16)使用串口向电脑发送数据
发送字节 发送数组 发送字符和字符串 字符: 字符串: 字符串在电脑中以字符数组的形式存储...

利用大模型技术进行测试用例推荐如何实现
利用大模型技术进行测试用例推荐,可以通过以下步骤实现: 确定目标和需求:明确测试用例推荐的目标和需求,例如推荐哪些类型的测试用例、推荐的数量、推荐的准确率等。 收集数据:收集历史测试用例、需求文档、设计文档等…...
Linux学习:初识Linux
目录 1. 引子:1.1 简述:操作系统1.2 学习工具 2. Linux操作系统中的一些基础概念与指令2.1 简单指令2.2 ls指令与文件2.3 cd指令与目录2.4 文件目录的新建与删除指令2.5 补充指令1:2.6 文件编辑与拷贝剪切2.7 文件的查看2.8 时间相关指令2.9 …...

Python CGI编程错误汇总
文章目录 1 前言2 测试文件3 问题总结 1 前言 在学习Python CGI编程时,运行起来总是有各种各样的问题,故将问题进行总结,以便新接触Python的童鞋能少走弯路 以下均为本人遇到对应报错的解决方案,可能存在其他问题但报错相同的情况…...

第十三届蓝桥杯大赛软件赛省赛C/C++ 大学 B 组 统计子矩阵
#include<iostream> #include<algorithm> #include<cstring> #include<string> #include<vector> #include<queue>using namespace std;int cnt,temp; int n,m,K; int a[505][505]; int pre[505][505];//二维前缀和void sol() {cin>>…...
计算机网络实验 基于ENSP的协议分析
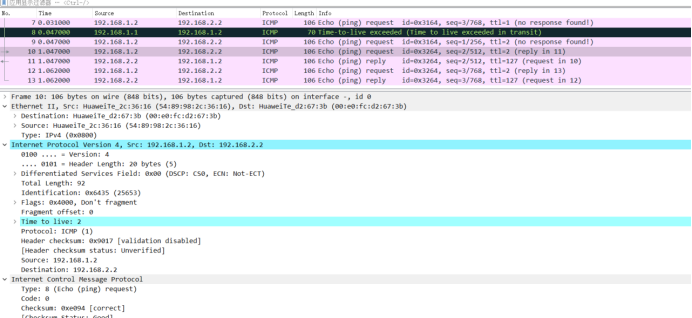
实验二 基于eNSP的协议分析 一、实验目的: 1)熟悉VRP的基本操作命令 2)掌握ARP协议的基本工作原理 3)掌握IP协议的基本工作原理 4)掌握ICMP协议的基本工作原理 二、实验内容: 1、场景1:两台PC机…...

Java实现手机库存管理
一、实验任务 编写一个程序,模拟库存管理系统。该系统主要包括系统首页、商品入库、商品显示和删除商品功能。每个功能的具体要求如下: 1.系统的首页:用于显示系统所有的操作,并且可以选择使用某一个功能。 2.商品入库功能&…...
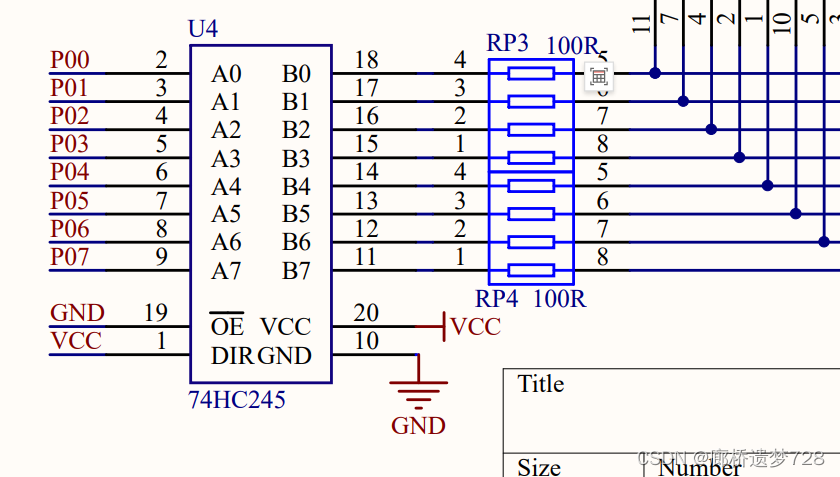
单片机入门:LED数码管
LED数码管 LED数码管:由多个发光二极管封装在一起组成的“8”字型的器件。如下图所示: 数码管引脚定义 一位数码管 内部由八个LED组成。器件有十个引脚。 对于数码管内的8个LED有共阴和共阳两种连接方法。 共阴:将8个LED的阴极都连接到一…...

软考信息系统项目管理师零基础怎么学习?
软考考信息系统项目管理师,零基础怎么入手高项? 要我说对于没有基础的人群来说零基础考信息系统项目管理师还是有一定的难度的,难就难在需要时间去了解基础,而相对于系统分析师、系统构架设计师、网络规划设计师、系统规划与管理…...
【轮式平衡机器人】——TMS320F28069片内外设之Timer_IT(补:CCS程序烧录方法)
引入 Timer_IT 指的是 TMS320F28069 的定时器中断功能。在微控制器或数字信号控制器中,定时器是一个非常重要的外设,它可以用来产生固定时间间隔的中断,或者用来精确计算时间。 Timer_IT 的主要特点如下: 定时功能:…...

安装Proxmox VE虚拟机平台
PVE是专业的虚拟机平台,可以利用它安装操作系统,如:Win、Linux、Mac、群晖等。 1. 下载镜像 访问PVE官网,下载最新的PVE镜像。 https://www.proxmox.com/en/downloads 2. 下载balenaEtcher balenaEtcher用于将镜像文件&#…...
后端项目访问不了
问题: 后端启动不了,无法访问网站 原因: 1.防火墙没有关 2.有缓存 3、项目没有启动 4、docker没有启动 解决: 先查看进程:docker ps,必须有三个 详细查看:docker ps -a exited代表没有开启…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
