【C++】位图+哈希切割+布隆过滤器
文章目录
- 一、位图
- 1.1 位图概念
- 1.2 位图实现
- 1.2.1 把x对应比特位0置1
- 1.2.2 把x对应比特位1置0
- 1.2.1 查看x对应比特位
- 1.3 位图源码
- 1.4 位图的应用
- 二、哈希切割(处理海量数据)
- 三、布隆过滤器
- 3.1 布隆过滤器的概念
- 3.2 布隆过滤器的应用场景
- 3.3 布隆过滤器的实现
- 3.3.1 布隆过滤器长度的设置
- 3.3.2 插入操作
- 3.3.3 查找操作
- 3.3.4 误判测试
- 3.3.5 布隆过滤器删除
- 3.4 布隆过滤器的应用
一、位图
先看一道例题:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
首先要知道,1G约等于10亿字节
那么40亿个整形就是160亿个字节,约等于16G。
【遍历或者排序+二分】 他们都需要存入数组中,但是内存没有空间能够创建16G大小的数组。(❌)
【红黑树和哈希】 红黑树不仅要存放数字,还得存放指针。(❌)
而哈希表也要存放指针和负载因子。(❌)
1.1 位图概念
【位图】 数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,我只需要判断在还是不在即可。那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。(✔)
我们知道无符号整数的范围是0 ~ 2^32 - 1,所以我们开一个2^32大小的数组。也就是2^32个比特位,因为一个整形是32个比特位,所以用位图开出的空间大小为:16G/32 = 0.5G = 512M。
接下来我们就可以使用直接定址法是几就在第几个位置把该比特位置为1。
而我们开int类型和char类型都无所谓,如果是char,就是8个比特位,第一个元素就可以表示0 ~ 7,第二个元素则表示8 ~ 15。如果是int类型就是32个比特位,第一个元素就可以表示0 ~ 31,第二个元素则表示32 ~ 63。
当我们要查找一个值x的时候,我们需要知道它在第几个元素的第几个比特位上,怎么办呢?
【char】在第x/8个元素上。在该元素的第x%8个比特位上。
【int】在第x/32个元素上。在该元素的第x%32个比特位上。
1.2 位图实现
这里我们使用vector<char>类型的位图。
那么我们首先就要初始化好:把每个比特位都置为0,那么vector开多大呢?
我们可以使用非类型模板参数,
template <size_t N>,那么我们就要开N / 8 + 1大小的空间。
template <size_t N>
class BitSet
{
public:BitSet(){_bits.resize(N / 8 + 1, 0);}
private:vector<char> _bits;
};
1.2.1 把x对应比特位0置1
我们按照上面说的/8和%8获得具体位置,加下来我们需要把这个位置置为1,其他位置不变,我们可以把1左移然后|=运算。
有人可能会如果是int类型,就跟大小端有关系,其实不管是大端还是小端。
左移是向高位移动
右移是向低位移动
void set(size_t x)
{size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);
}
1.2.2 把x对应比特位1置0
我们只能把x对应的比特位变成0,其他位置不能变,那么我们可以先用上面的方法找到位置,然后将1左移然后先取反再&=运算
void reset(size_t x)
{size_t i = x / 8;size_t j = x % 8;_bits[i] &= (~(1 << j));
}
1.2.1 查看x对应比特位
还是按照上面的方法找到具体位置后,把1左移到该位置,返回两个&的结果。
bool search(int x)
{size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);
}
1.3 位图源码
namespace yyh
{template <size_t N>class BitSet{public:BitSet(){_bits.resize(N / 8 + 1, 0);}void set(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 8;size_t j = x % 8;_bits[i] &= (~(1 << j));}bool search(int x){size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);}private:std::vector<char> _bits;};
}
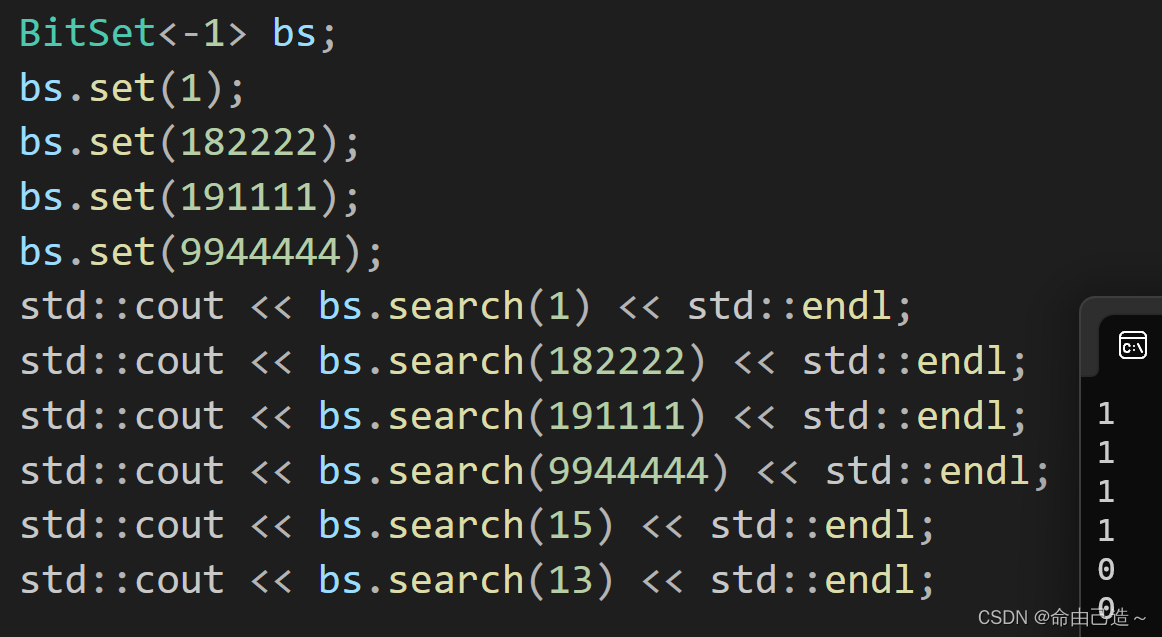
上面就是为了开辟42亿个比特的大小,因为-1的无符号数字就是2^32 - 1,当然也可以写成0xffffffff。
验证一下所占内存大小:

1.4 位图的应用
【第一题】
给定100亿个整数,设计算法找到只出现一次的整数?
这里的关键是注意到只出现一次,这样我们就可以列出三种状态:
1️⃣ 出现0次
2️⃣ 出现1次
3️⃣ 出现1次以上
我们只需要两个比特位就可以表示出三个状态。
上面的位图是用一个位图中的一个比特位标定一个数字出没出现,那么这里我们可以用两个位图的两个比特位标定一个数字出现次数。
假如现在是看0这个数字:
template <size_t N>
class TwoBitSet
{
public:void set(size_t x){if (!_b1.search(x) && !_b2.search(x))// 00{_b2.set(x);// 01}else if (!_b1.search(x) && _b2.search(x))// 01{_b1.set(x);_b2.reset(x);// 10}// 10不变}void PrintOnce(){for (size_t i = 0; i < N; i++){if (!_b1.search(i) && _b2.search(i))std::cout << i << std::endl;}}private:BitSet<N> _b1;BitSet<N> _b2;
};
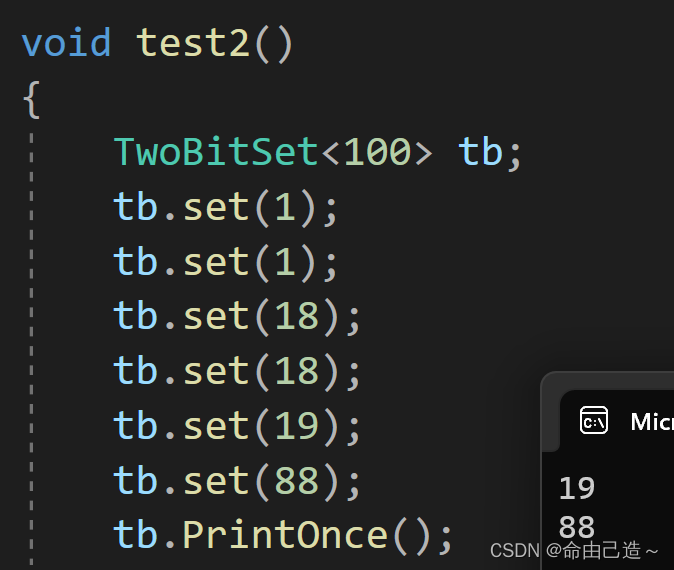
【第二题】
给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
思路一: 先把一个位图中的数据放入位图中,然后遍历另一个文件寻找,找出交集。
但是有可能会出现重复元素,要注意去重。
思路二: 两个文件的元素放进两个位图中,放进去的过程就各自去重了,然后两个&运算即可判断是否有交集。
【第三题】
1 个文件有 100 亿个 int,1G内存,设计算法找到出现次数不超过2次的所有整数
这个题跟第一题类似,可以分为四种状态:
1️⃣ 出现0次
2️⃣ 出现1次
3️⃣ 出现2次
4️⃣ 出现3次以上
所以一样可以用两个位图表示四种状态。
【第四题】
给一个超过100G大小的log file,log中存着IP地址,设计算法找到出现次数最多的IP地址
这里就不能用位图了,因为位图的作用是统计在不在,统计次数还得使用map。
我们可以把文件切分成多个小文件,这里的切分也是有讲究的,如果平均切分,在每个小文件统计的话结果不正确,因为可能一个IP有多份分在多个文件。而我们map统计完一个小文件就要清空再统计下一个文件,不然内存不够用。
所以这里我们需要使用哈希切割。
二、哈希切割(处理海量数据)
前面我们学过为了实现哈希映射,我们需要一个哈希函数,这里我们也可以使用哈希函数把IP转为整型。比方说我们分成了100份小文件,idx = HashFunc(IP) % 100,idx是几就把它放进几号文件中。
我们可以把每个小文件理解为一个哈希桶。
这样不一样的IP可能分进同一个小文件中,但是同一个IP一定会分进同一个小文件。
这里还可能出现一个情况:其中一个小文件的大小可能超过1G(假设超过1G就不够了)。
而超过了1G也有有两种情况:
1️⃣ 不重复的IP很多,map需要很多节点,统计不下。
2️⃣ 重复的IP很多,map不需要很多节点,统计的下。
针对第一种情况,我们可以换个哈希函数递归切分。
但是这种方法对情况二无效,因为相同的IP太多,照样会切分超过1G。
所以综合考虑可以这样统计:
不管是啥情况,都直接用map统计,如果是第二种情况就直接统计完成了。如果是第一种情况,会insert失败,我们可以捕获异常,此时再去换个哈希函数递归切分。
三、布隆过滤器
通过上面的讲解我们可以看出
位图的优点是节省空间和效率高
缺点是要求范围相对集中,而且只能是整型。
而如果是字符串我们想使用位图,就可以使用哈希函数转成整型。
这里就会有一种情况,不同的字符串可能转换成同一个整型。 会导致误判。
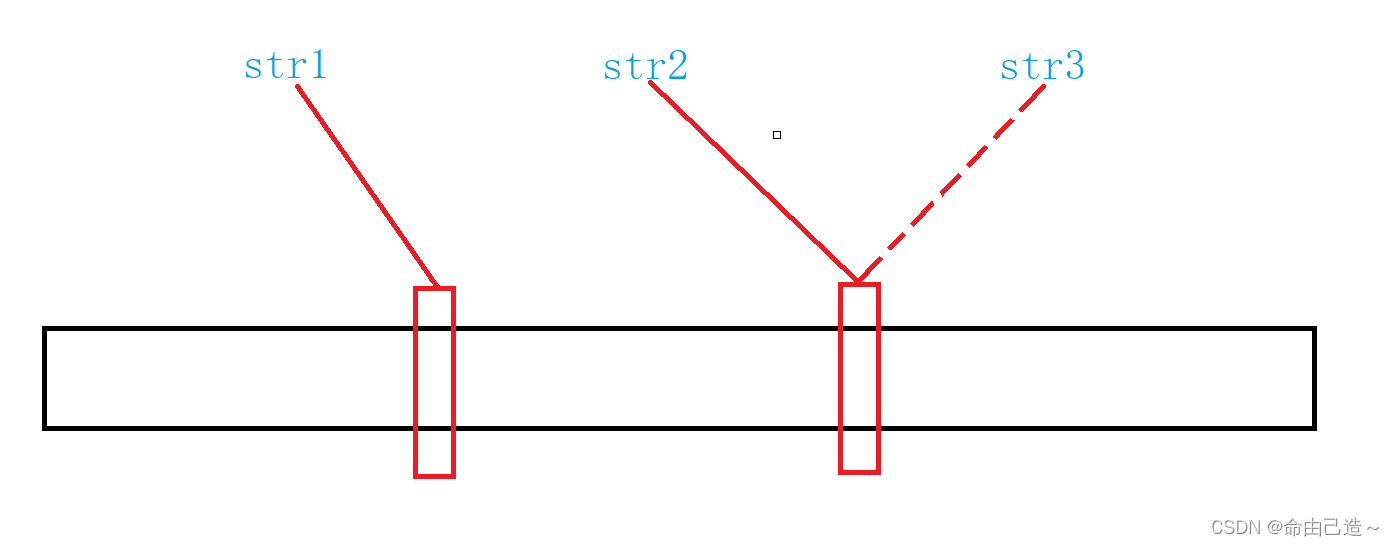
存在是不准确的,如果只有str1和str2,而str3映射的位置跟str2重了,就会导致原本不在的元素误判成在。
那我们如何降低误判率呢?答案是使用布隆过滤器。
3.1 布隆过滤器的概念
它的主要思想是让一个值映射多个位置。我们可以使用多个哈希函数,多映射几个位置,这里假设有两个哈希函数,映射两个位置。
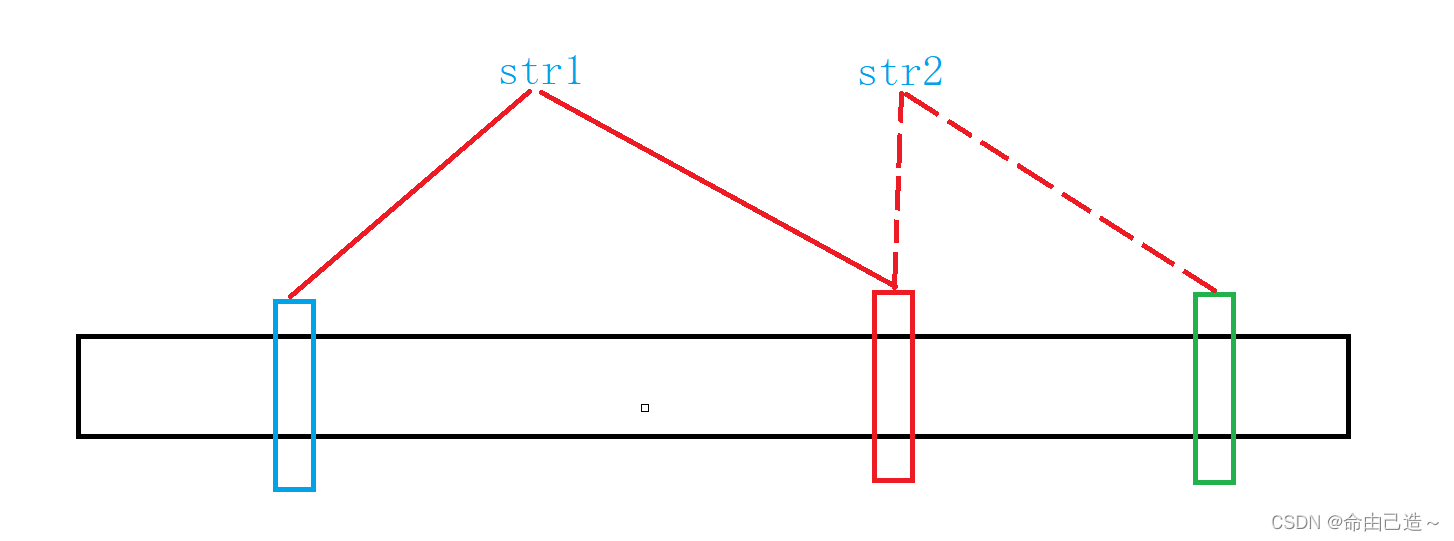
这样我们要看str2是否存在,必须要同时指向红色和绿色才能判断为存在。
所以布隆过滤器的作用就是降低误判率。映射的位置越多,误判率越低。
但是这里映射的位置也不能太多,映射的多,占的空间也多,找的次数也多,我们使用位图这样的方式就是为了提高效率并且节省空间。映射的多了也就没那么节省空间了。
3.2 布隆过滤器的应用场景
【场景一】
当我们要写一个注册系统的时候,我们注册昵称的时候不能跟别人重复,此时我们就可以采用布隆过滤器,如果不在那么就是准确的,一定不存在。但是如果显示存在,则有可能是误判。因为布隆过滤器中如果存在可能会误判,可以到数据库中再次查询昵称号码存不存在。
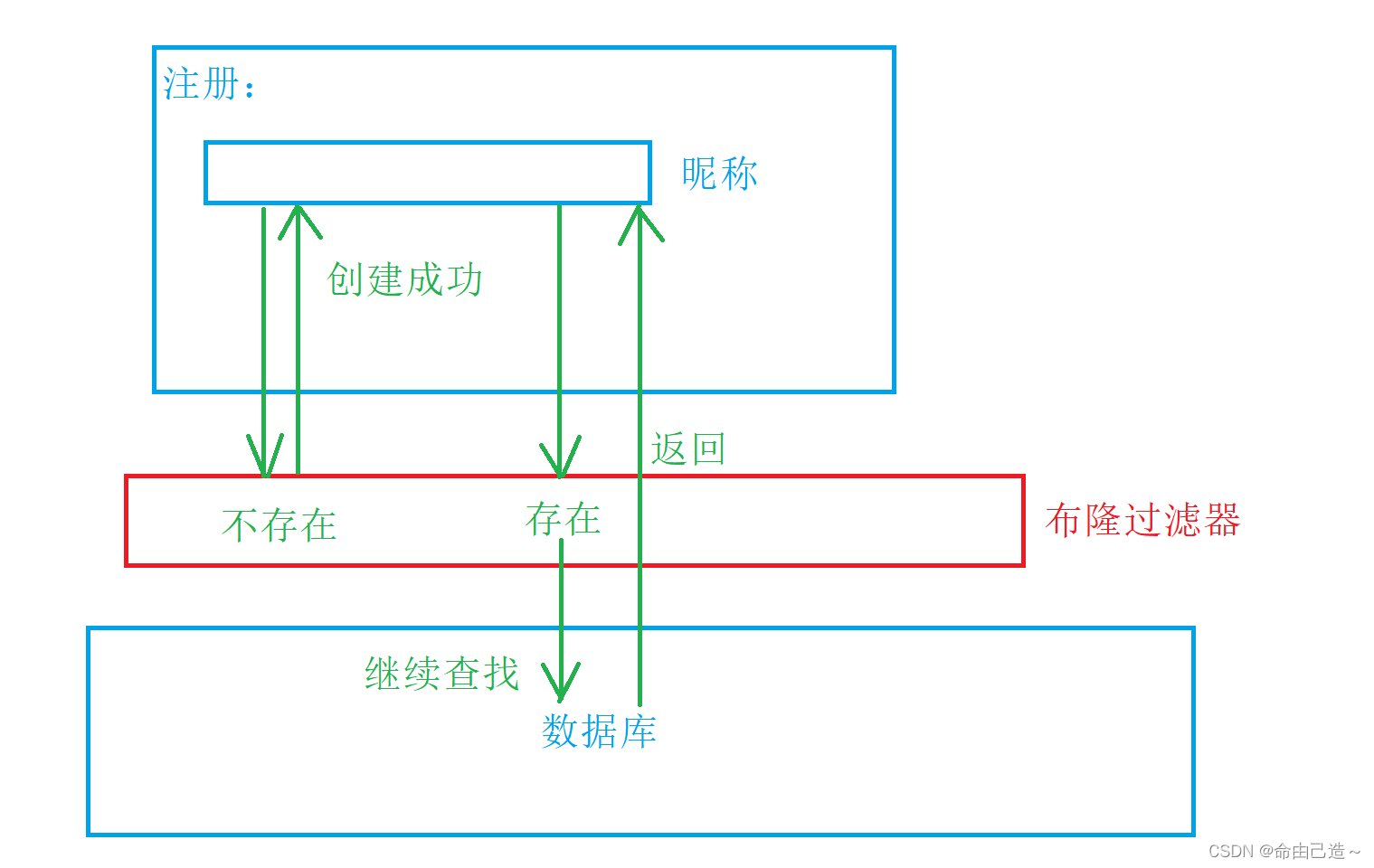
有人可能问这有必要加一个布隆过滤器吗?
假设现在来了100不存在的值,大部分都会显示不存在,只有很小一部分会误判为存在,这样没有误判的大部分效率大大提高。
【场景二】
我们在访问网站的时候有时候会出现风险网站。我们可以把这些网页加入黑名单,在我们访问网站之前就先经过布隆过滤器,有风险就可以快速的判断。
3.3 布隆过滤器的实现
布隆过滤器最常见的是string类型。 这里要给一个非类型模板参数N以确定开的空间有多大,这里我们写三个哈希函数。而字符串转整型的哈希函数有很多:
各种字符串Hash函数
这里我们就取里面效率较高的三个:
struct BKDRHash
{size_t operator()(const std::string& s){size_t value = 0;for (auto ch : s){value *= 31;value += ch;}return value;}
};struct APHash
{size_t operator()(const std::string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){if ((i & 1) == 0){hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const std::string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};
3.3.1 布隆过滤器长度的设置
关于长度的问题这里有专门的文章进行讲述:
详解布隆过滤器的原理
里面有一个公式:

这里n我们是知道的,假设k是3,ln2约等于0.7,最后得到m=4.2*n,所以布隆过滤器多一个数据要开大约4.2个比特位,我们直接按加入一个数据开5个比特位算。
template<size_t N,
class K = std::string,
class HashFunc1 = BKDRHash,
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>
class BloomFilter
{
public:
private:std::bitset<N * 5> _bs;
};
3.3.2 插入操作
大致思路跟我们上面的位图一样,这里我们使用库里的函数bitset头文件:#include <bitset>而set函数库里面已经帮我们实现好了:
void set(const K& x)
{size_t idx1 = HashFunc1()(x) % (5 * N);size_t idx2 = HashFunc2()(x) % (5 * N);size_t idx3 = HashFunc3()(x) % (5 * N);_bs.set(idx1);_bs.set(idx2);_bs.set(idx3);
}
3.3.3 查找操作
这里只要有一处不在那么就返回false,全部都在才能返回true。
bool test(const K& x)
{size_t idx1 = HashFunc1()(x) % (5 * N);if (!_bs.test(idx1)){return false;}size_t idx2 = HashFunc2()(x) % (5 * N);if (!_bs.test(idx2)){return false;}size_t idx3 = HashFunc3()(x) % (5 * N);if (!_bs.test(idx3)){return false;}return true;
}
3.3.4 误判测试
std::string arr[] = { "北京", "武汉", "广州", "上海", "北京", "北京", "广州","上海", "上海" };BloomFilter<10> bs;for (auto& e : arr){bs.set(e);}for (auto& e : arr){std::cout << bs.test(e) << std::endl;}std::cout << std::endl;
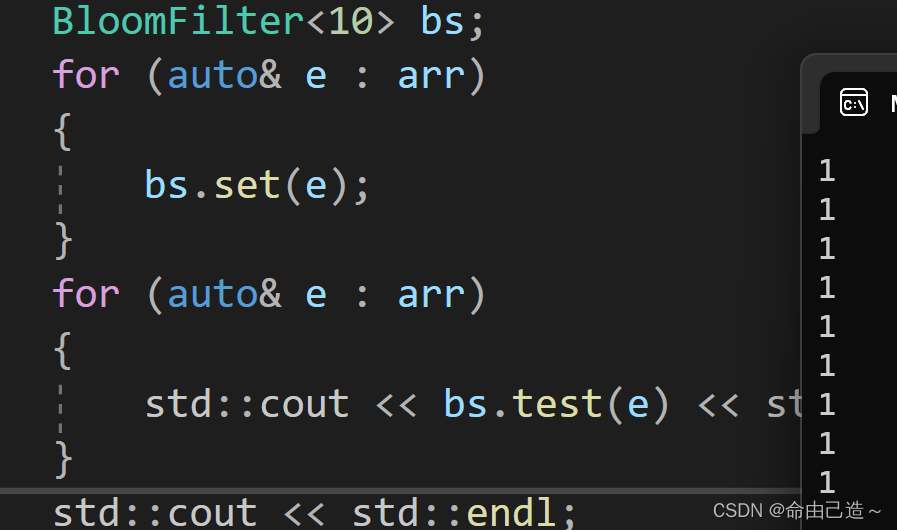
结果没有问题,接下来我们测试误判,加上:
// 测试误判
srand(time(0));
for (auto& e : arr)
{std::cout << bs.test(e + std::to_string(rand())) << std::endl;
}
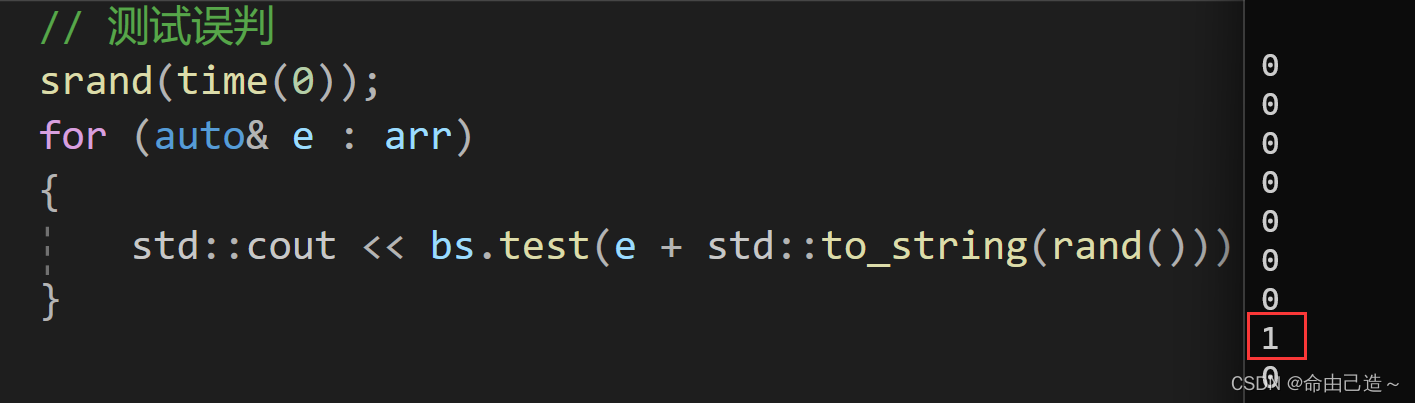
可以看到出现了误判。
3.3.5 布隆过滤器删除
布隆过滤器一般不能支持删除,因为一个位置可能被多个值映射,删除以后可能把别人的也删掉了。
那么我们能不能强制支持删除呢?
我们可以去计数,有几个值映射计数器就是几,删除了就让当前位置的计数器
--。
但是使用计数又会有问题:因为不知道计数器的范围,所以不能开的太小的比特位,导致使用过多内存。
3.4 布隆过滤器的应用
【第一题】
给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和 近似算法。(query就是sql语句,可以理解为一个字符串。,也可能是网络请求url,也就是网址)
近似算法我们直接使用布隆过滤器,将一个文件的query语句放进布隆过滤器里,然后另一个文件查找在不在就是交集。虽然有误判:不存在的也被当做交集。但是作为近似算法还是可行的。
而精确算法就得用到前面的哈希切割。同时把两个文件都切分成数个小文件,在编号相同的小文件查看交集即可,最后注意去重。
相关文章:

【C++】位图+哈希切割+布隆过滤器
文章目录一、位图1.1 位图概念1.2 位图实现1.2.1 把x对应比特位0置11.2.2 把x对应比特位1置01.2.1 查看x对应比特位1.3 位图源码1.4 位图的应用二、哈希切割(处理海量数据)三、布隆过滤器3.1 布隆过滤器的概念3.2 布隆过滤器的应用场景3.3 布隆过滤器的实…...
)
python实现网络游戏NPC任务脚本引擎(带限时任务功能)
python实现NPC任务脚本引擎 一、简介二、简单示例三、实现任务限时的功能四、结合twisted示例一、简介 要实现面向对象的网络游戏NPC任务脚本引擎,可以采用以下步骤: 1.定义NPC类:该类应该包括NPC的基本属性和行为,如名字、位置、血量、攻击力等等。NPC还应该有任务的列表…...
)
C语言的原子操作(待完善)
文章目录一、什么是原子操作二、为什么需要原子操作三、API一、什么是原子操作 原子操作是不可分割的,在执行完毕之前不会被任何其它任务或事件中断,可以视为最小的操作单元,是在执行的过程中、不会导致对数据的并发访问的、最小操作&#x…...

JavaScript Boolean 布尔对象
文章目录JavaScript Boolean 布尔对象Boolean 对象Boolean 对象属性Boolean 对象方法检查布尔对象是 true 还是 false创建 Boolean 对象JavaScript Boolean 布尔对象 Boolean(布尔)对象用于将非布尔值转换为布尔值(true 或者 false࿰…...
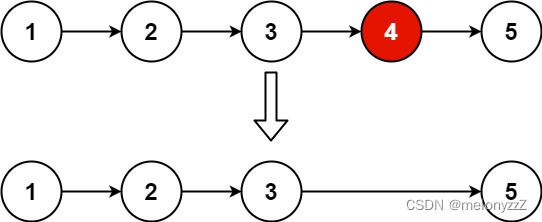
删除链表元素相关的练习
目录 一、移除链表元素 二、删除排序链表中的重复元素 三、删除排序链表中的重复元素 || 四、删除链表的倒数第 N 个结点 一、移除链表元素 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头…...

3DEXPERIENCE Works 成为了中科赛凌实现科技克隆环境的催化剂
您的企业是否想过实现设计数据的统筹管理,在设计上实现标准化,并把每位设计工程师串联起来协同办公?中科赛凌通过使用3DEXPERIENCE Works 实现了上述内容,一起来看本期案例分享吧!中科赛凌 通过其自主研发的单压缩机制冷技术实现零下190℃制…...

少儿编程 电子学会图形化编程等级考试Scratch一级真题解析(选择题)2022年12月
少儿编程 电子学会图形化编程等级考试Scratch一级真题解析2022年12月 选择题(共25题,每题2分,共50分) 1、小明想在开始表演之前向大家问好并做自我介绍,应运行下列哪个程序 A、 B、 C、 D、 答案:D...

【完整版】国内网络编译,Ambari 2.7.6 全部模块源码编译笔记
本次编译 ambari 2.7.6 没有使用科学上网的工具,使用的普通网络,可以编译成功,过程比 ambari 2.7.5 编译时要顺畅。 以下是笔记完整版。如果想单独查看本篇编译笔记,可参考:《Ambari 2.7.6 全部模块源码编译笔记》 该版本相对 2.7.5 版本以来,共有 26 个 contributors …...

HTML 颜色值
HTML 颜色值 颜色由红 (R)、绿 (G)、蓝 (B) 组成。 颜色值 颜色值由十六进制来表示红、绿、蓝(RGB)。 每个颜色的最低值为 0 (十六进制为 00 ),最高值为 255 (十六进制为 FF )。 十六进制值的写法为#号后跟三个或六个十六进制字符。 三位…...

RabbitMQ-消息的可靠性投递
文章目录0. 什么是消息的可靠性投递1. confirm机制2. return机制3. 总结0. 什么是消息的可靠性投递 在生产环境中,如果因为一些不明原因导致RabbitMQ重启,RabbitMQ重启过程中是无法接收消息的,那么我们就需要生产者重新发送消息。或者在消息…...
| 含思路)
华为OD机试题 - 最小叶子节点(JavaScript)| 含思路
华为OD机试题 最近更新的博客使用说明本篇题解:最小叶子节点题目输入输出示例一输入输出示例二输入输出Code解题思路华为OD其它语言版本最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD…...
)
嵌入式系统硬件设计与实践(开发过程)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 如果把电路设计看成是画板子的,这本身其实是狭隘了。嵌入式硬件设计其实是嵌入式系统中很重要的一个部分。里面软件做的什么样…...
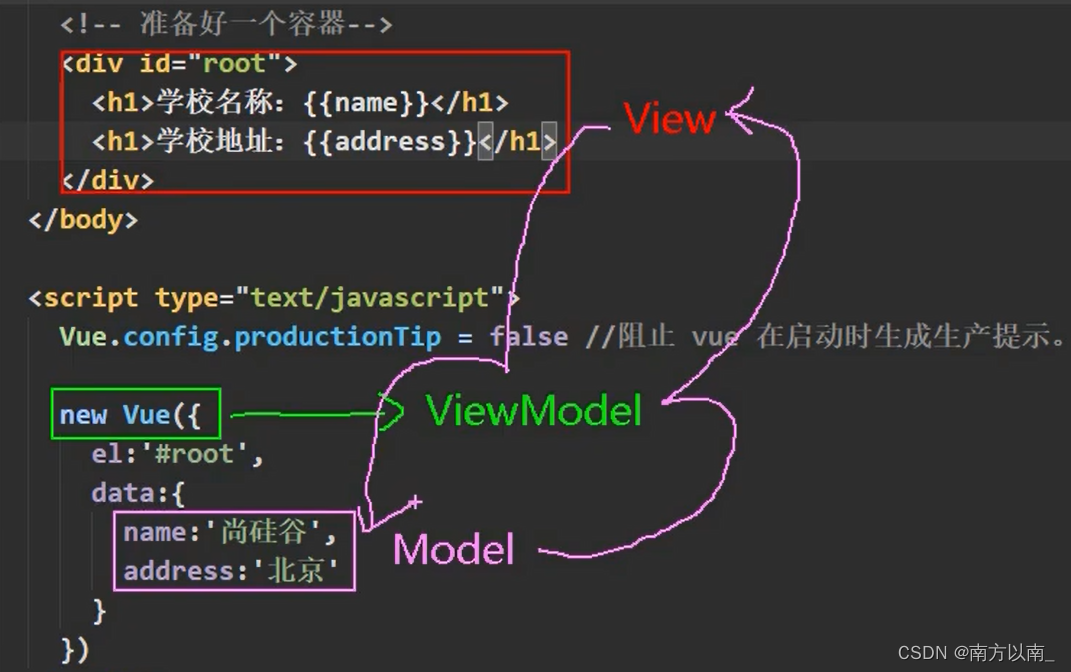
入门vue(1-10)
正确学习方式:视频->动手实操->压缩提取->记录表述 1基础结构 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"&…...

C#开发的OpenRA的游戏主界面怎么样创建3
继续游戏主界面创建的主题, 我们知道游戏的主界面上有很多部件,比如显示文本的标签(LabelWidget), 显示按钮(ButtonWidget)。那么这些部件又是如何创建在主界面上的呢? 其实这些部件是否显示,都是来源于文件yaml,在这里就是文件mainmenu.yaml, 在这个文件里定义了所有…...

秒懂算法 | 基于主成分分析法、随机森林算法和SVM算法的人脸识别问题
本文的任务与手写数字识别非常相似,都是基于图片的多分类任务,也都是有监督的。 01、数据集介绍与分析 ORL人脸数据集共包含40个不同人的400张图像,是在1992年4月至1994年4月期间由英国剑桥的Olivetti研究实验室创建。 此数据集下包含40个目录,每个目录下有10张图像,每个…...
QML Loader(加载程序)
Loader加载器用于动态加载 QML 组件。加载程序可以加载 QML 文件(使用 source 属性)或组件对象(使用 sourceComponent 属性) 常用属性: active 活动asynchronous异步,默认为falseitem项目progress 进度so…...

C++——类型转换
目录 C语言中的类型转换 C强制类型转换 static_cast reinterpret_cast const_cast dynamic_cast 延伸问题 RTTI(了解) C语言中的类型转换 在C语言中,如果赋值运算符左右两侧类型不同,或者形参与实参类型不匹配,或…...

vue3:生命周期(onErrorCaptured)
一、背景 当项目如果发生报错,影响程序体验。如果能以捕获的方式得到错误信息,而且还能定位问题,这样就好了,本文介绍onErrorCaptured实现我们想要的效果。 vue2:errorCaptured。使用与vue3同理。 vue3:…...

vue过滤器
vue 过滤器 对要显示的数据进行特定格式化之后再显示 注册过滤器 Vue.filter(name,callback)new Vue({filters:{}}) 使用过滤器 {{ name | 过滤器名 }}v-band:属性“name | 过滤器名” 局部过滤器 <p>{{time | timeFormater }}</p> <!-- 过滤器可接受额外参…...

I/O模型
写在前面 前面聊完了IO方式, 也就意味着网络数据的收发通道是建立起来了。但业务场景中, 通道本身是不会发送数据的。在常见的网络应用中, server端会创建多个链接以服务更多client, 同时要求各个client尽可能互不影响。这是I/O模型(也就是IO方式线程模型)要解决的问题。由于加…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...
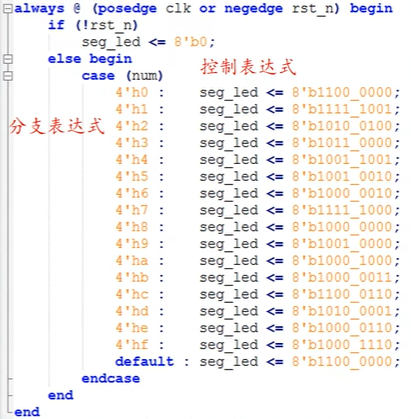
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...