基础算法|线性结构|前缀和学习
参考文章:
https://blog.csdn.net/weixin_72060925/article/details/127835303
二维数组的前缀和练习:
这里要注意的地方就是求子矩阵和的时候,这里要减去的是x1-1,y1-1的部分,因为所求的目标值是包括边界的
//前缀和基础练习 #include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5*1e3+10;
int n,m,q;
int nums[N][N]={0};
int s[N][N]={0};
signed main() {scanf("%d %d %d",&n,&m,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&nums[i][j]);s[i][j]=s[i][j-1]+s[i-1][j]+nums[i][j]-s[i-1][j-1];}}while(q--){int x1,y1,x2,y2;scanf("%d %d %d %d",&x1,&y1,&x2,&y2);int ans=0;//注意这里要减去的是x1-1,y1-1的部分,因为所求的目标值是包括边界的 ans=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];cout<<ans<<endl;}return 0;
}测试:
/*
输入:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出:
17
27
21*/ 相关文章:

基础算法|线性结构|前缀和学习
参考文章: https://blog.csdn.net/weixin_72060925/article/details/127835303 二维数组的前缀和练习: 这里要注意的地方就是求子矩阵和的时候,这里要减去的是x1-1,y1-1的部分,因为所求的目标值是包括边界的 //前缀…...
设计模式之模版方法实践
模版方法实践案例 实践之前还是先了解一下模版方法的定义 定义 模板方法模式是一种行为设计模式,它定义了一个骨架,并允许子类在不改变结构的情况下重写的特定步骤。模板方法模式通过在父类中定义一个模板方法,其中包含了主要步骤…...

sql中COALESCE函数详解
在SQL中,COALESCE函数是一个非常有用的函数,用于从其参数列表中返回第一个非NULL值。如果所有给定的参数都是NULL,那么COALESCE函数将返回NULL。这个函数可以接受多个参数,使其在处理可能出现的NULL值时非常灵活和强大。 语法 C…...

rust-analyzer报错“Failed to spawn one or more proc-macro servers,....“怎么解决?
最近,在使用vscode测试rust代码时,遇到了一些问题。在经过反复折腾后,最终解决了问题,在此写下作为记录,以便于以后参考。 我遇到的报错内容是: Failed to spawn one or more proc-macro servers. cannot find proc-macro-srv, the workspace E:\100rust\temp is missin…...

Communications--9--一文读懂双机热备冗余原理
1、热备冗余管理 2、主备系状态判断 3、如何从冷备做到热备? 参见: 用软件实现热备冗余信号系统的安全切换...

可调恒定电流稳压器NSI50150ADT4G车规级LED驱动器 提供专业的汽车级照明解决方案
NSI50150ADT4G产品概述: NSI50150ADT4G可调恒定电流稳压器 (CCR) ,是一款简单、经济和耐用的器件,适用于为 LED 中的调节电流提供成本高效的方案(与恒定电流二极管 CCD 类似)。该 (CCR) 基于自偏置晶体管 (SBT) 技术&…...

Unity中使用代码动态修改URP管线下的标准材质是否透明
//修改为透明 material.SetFloat("_Surface",1.0f); material.SetInt("_SrcBlend", (int)UnityEngine.Rendering.BlendMode.One); material.SetInt("_DstBlend", (int)UnityEngine.Rendering.BlendMode.OneMinusSrcAlpha); material.Set…...

关于制作Python游戏全过程(汇总1)
目录 前言: 1.plane_sprites模块: 1.1导入模块: 1.1.1pygame:一个用于创建游戏的Python库。 1.1.2random:Python标准库中的一个模块,用于生成随机数。 1.2定义事件代号: 1.2.1ENEMY_EVENT:自定义的敌机出场事件代号…...

独立站营销新纪元:AI与大数据塑造个性化体验的未来
随着全球互联网的深入发展和数字化转型的不断推进,作为品牌建设和市场营销的重要载体,独立站将迎来新的发展机遇。新技术的涌现,特别是人工智能和大数据等技术的广泛应用,为独立站带来了前所未有的机遇与挑战。本文Nox聚星将和大家…...

C语言项目实战——贪吃蛇
C语言实现贪吃蛇 前言一、 游戏背景二、游戏效果演示三、课程目标四、项目定位五、技术要点六、Win32 API介绍6.1 Win32 API6.2 控制台程序6.3 控制台屏幕上的坐标COORD6.4 GetStdHandle6.5 GetConsoleCursorInfo6.5.1 CONSOLE_CURSOR_INFO 6.6 SetConsoleCursorInfo6.7 SetCon…...
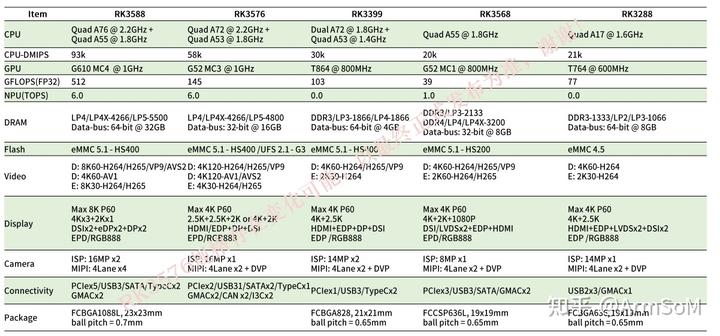
ArmSoM规划开发基于RK3576的开发套件
ArmSoM正计划推出一款新的产品,这款产品将采用强大的RK3576芯片。 本文将为您介绍我们的新产品搭载的RK3576性能参数,以及它如何为您提供卓越的性能和功能。 RK3576处理器 RK3576处理器是一款强大的处理器,具备出色的性能和多样化的功能&a…...
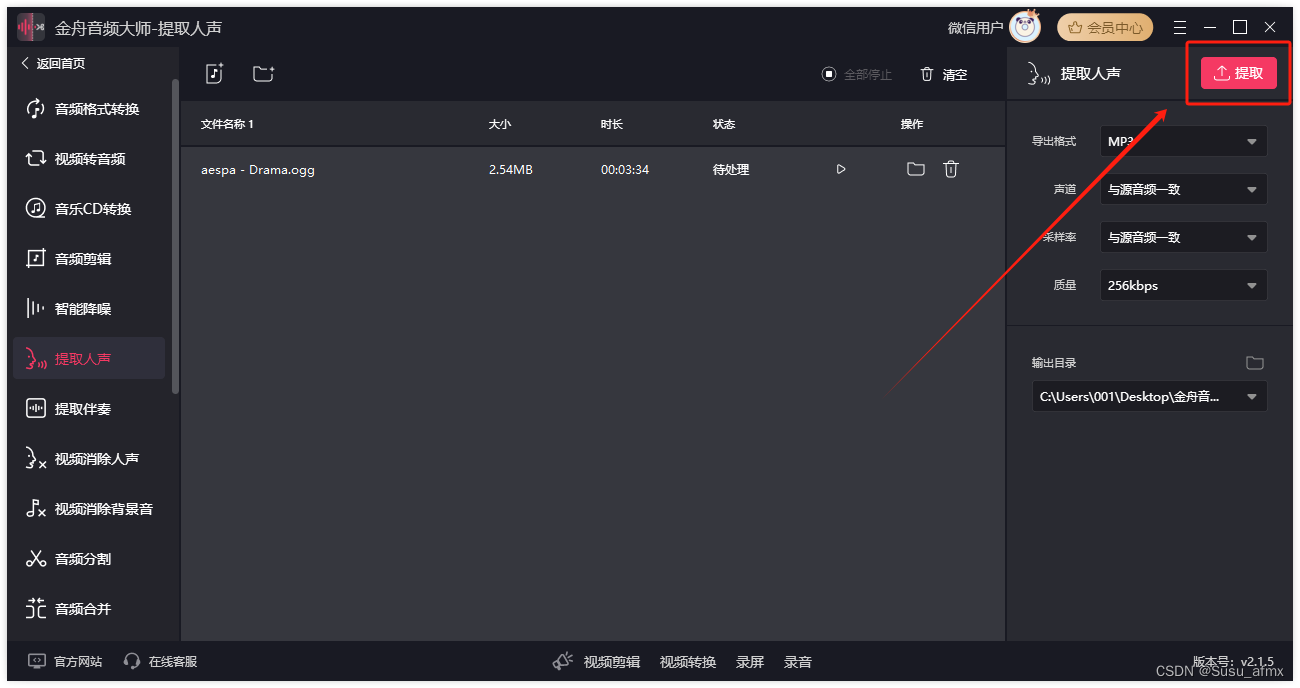
视频剪辑如何提取伴奏?短视频剪辑有妙方
在多媒体处理中,音频的编辑和处理是不可或缺的一部分。很多时候,我们可能想要从一段视频或音频中提取伴奏,或者实现人声的分离,以便于进一步制作或混音。以下,将为您介绍一种简单而有效的方法来实现这一目标。 一、提取…...
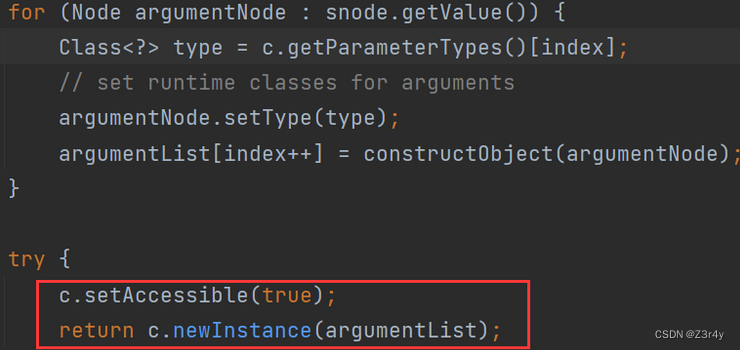
【Web】浅浅地聊SnakeYaml反序列化两条常见利用链
目录 关于Yaml 关于SnakeYaml SnakeYaml反序列化利用 JdbcRowSetImpl链 ScriptEngineManager链 复现 基本原理 继续深入 关于Yaml 学过SpringBoot开发的师傅都知道,YAML和 Properties 文件都是常见的配置文件格式,用于存储键值对数据。 这里举…...

详解openGauss客户端工具gsql的高级用法
前言: gsql是openGauss提供在命令行下运行的数据库连接工具,可以通过此工具连接服务器并对其进行操作和维护,除了具备操作数据库的基本功能,gsql还提供了若干高级特性,便于用户使用。 gsql的基本功能 连接数据库&…...
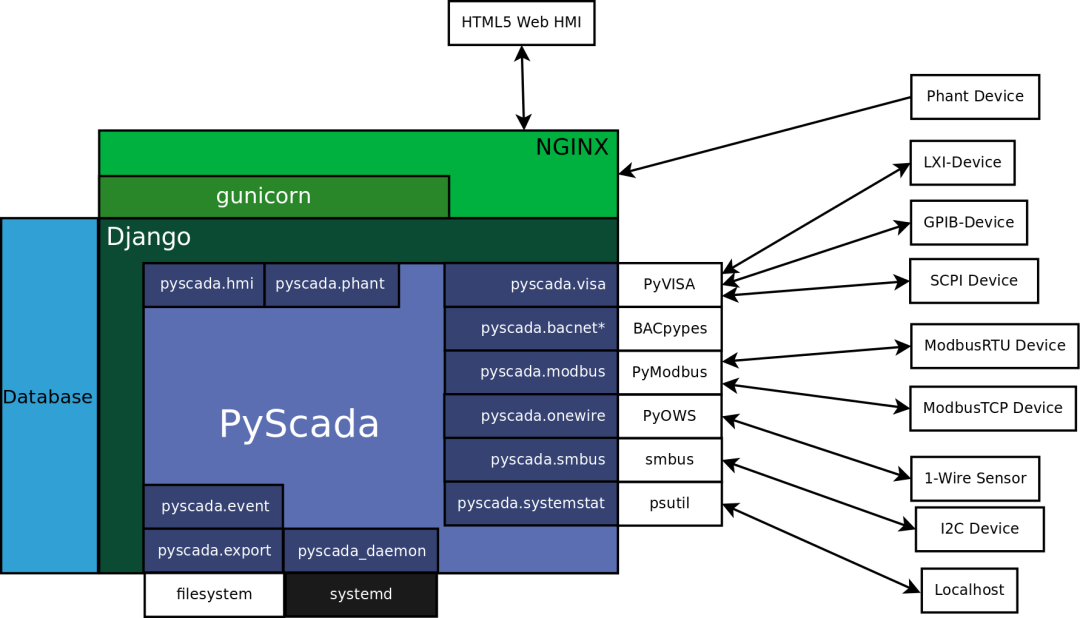
开源工业软件:SCADA系统开源
PyScada是一个开源的scada系统 源代码地址 http://www.gitpp.com/huangtomy/pyscada-cn SCADA系统是Supervisory Control And Data Acquisition的缩写,即数据采集与监视控制系统。它是以计算机为基础的DCS与电力自动化监控系统,应用领域非常广&#x…...

关于AI彩票预测算法的设想
本文以双色球选择红色6个号码为例 我们先把问题简化,双色球红色号码一共有33个球。摇奖时,每次随机摇出来一个号码,连续6次,就随机出来了6个红色球号码。 而这6个号码就是一注彩票里的前6个红色球号码。这里不讨论一注彩票里后端…...

设计模式之策略模式实践
设计模式之策略模式实践 先了解一下策略模式的定义是什么?解决什么问题 策略模式是一种行为设计模式,它定义了一系列算法,将每个算法封装成一个类,并使它们可以互相替换。策略模式允许客户端在运行时从可互换的算法中选择一个&a…...

讨论:解决哈希冲突的几种方法
1. 什么是哈希 哈希是通过对数据进行再压缩,提高效率的一种解决方法。 2. 什么时候会产生哈希冲突 通过哈希函数产生的哈希值是有限的,当数据量比较大时经过哈希函数处理后仍然有不同的数据对应相同的值。这时候就产生了哈希冲突。 3. 常见的哈希函数 1&…...
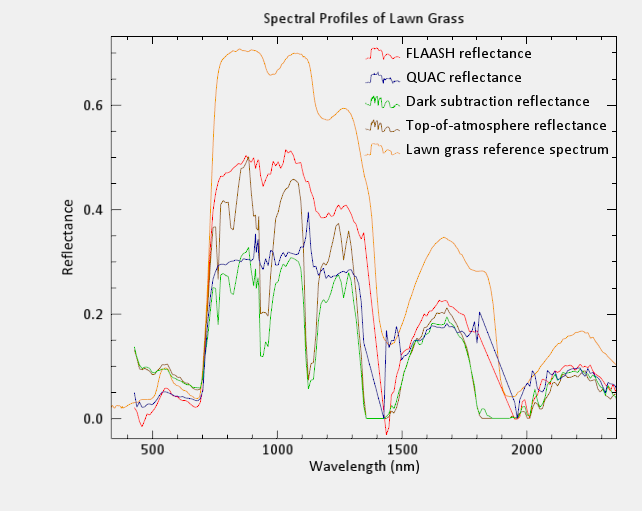
遥感分析时什么情况下需要做大气校正?
经常会遇到这样的问题:什么情况需要做大气校正产生?这个问题取决于传感器和应用目标,总的来说,如果要做光谱分析,那么大气校正是必须要做的。本文对于在什么情况下选择什么样的大气校正方法,给出了一些依据…...

设计模式学习笔记 - 设计原则 - 7.DRY 原则及提高代码复用性
前言 DRY 原则,英文描述为: Don’t Repeat Yourself。中文直译:不要重复自己。将它应用在编程中,可理解为:不要写重读的代码。 可能你认为,这个原则很简单。只要两段代码长得一样,那就是违反 …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
