LeetCode 2917.找出数组中的 K-or 值:基础位运算
【LetMeFly】2917.找出数组中的 K-or 值:基础位运算
力扣题目链接:https://leetcode.cn/problems/find-the-k-or-of-an-array/
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
nums 中的 K-or 是一个满足以下条件的非负整数:
- 只有在
nums中,至少存在k个元素的第i位值为 1 ,那么 K-or 中的第i位的值才是 1 。
返回 nums 的 K-or 值。
注意 :对于整数 x ,如果 (2i AND x) == 2i ,则 x 中的第 i 位值为 1 ,其中 AND 为按位与运算符。
示例 1:
输入:nums = [7,12,9,8,9,15], k = 4 输出:9 解释:nums[0]、nums[2]、nums[4] 和 nums[5] 的第 0 位的值为 1 。 nums[0] 和 nums[5] 的第 1 位的值为 1 。 nums[0]、nums[1] 和 nums[5] 的第 2 位的值为 1 。 nums[1]、nums[2]、nums[3]、nums[4] 和 nums[5] 的第 3 位的值为 1 。 只有第 0 位和第 3 位满足数组中至少存在 k 个元素在对应位上的值为 1 。因此,答案为 2^0 + 2^3 = 9 。
示例 2:
输入:nums = [2,12,1,11,4,5], k = 6 输出:0 解释:因为 k == 6 == nums.length ,所以数组的 6-or 等于其中所有元素按位与运算的结果。因此,答案为 2 AND 12 AND 1 AND 11 AND 4 AND 5 = 0 。
示例 3:
输入:nums = [10,8,5,9,11,6,8], k = 1 输出:15 解释:因为 k == 1 ,数组的 1-or 等于其中所有元素按位或运算的结果。因此,答案为 10 OR 8 OR 5 OR 9 OR 11 OR 6 OR 8 = 15 。
提示:
1 <= nums.length <= 500 <= nums[i] < 2311 <= k <= nums.length
方法一:基础位运算

想AC这道题,只需要懂得两个位运算操作:
- 计算 t t t二进制下第 i + 1 i+1 i+1位是否为 1 1 1:KaTeX parse error: Expected 'EOF', got '&' at position 10: (t >> i) &̲ 1
- 将 a n s ans ans二进制下的第 i + 1 i+1 i+1位置为 1 1 1: a n s ∣ = ( 1 < < i ) ans |= (1 << i) ans∣=(1<<i)
因 0 ≤ n u m s [ i ] ≤ 2 31 0\leq nums[i] \le 2^{31} 0≤nums[i]≤231,所以用变量 i i i从 0 0 0到 30 30 30枚举每一位,统计所有数字中这一位为 1 1 1的个数,若达到 k k k则令答案的这一位为 1 1 1。
- 时间复杂度 O ( l e n ( n u m s ) × log n u m s [ i ] ) O(len(nums)\times \log nums[i]) O(len(nums)×lognums[i]),其中 log n u m s [ i ] = 31 \log nums[i]=31 lognums[i]=31
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
public:int findKOr(vector<int>& nums, int k) {int ans = 0;for (int i = 0; i < 32; i++) { // nums[i] < 2^31不是≤,因此这里其实i = 0到i < 31即可int cnt = 0;for (int t : nums) {cnt += ((t >> i) & 1);}if (cnt >= k) {ans |= (1 << i);}}return ans;}
};
Python
# from typing import Listclass Solution:def findKOr(self, nums: List[int], k: int) -> int:ans = 0for i in range(31):cnt = 0for t in nums:cnt += ((t >> i) & 1)if cnt >= k:ans |= (1 << i)return ans
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/136497896
相关文章:

LeetCode 2917.找出数组中的 K-or 值:基础位运算
【LetMeFly】2917.找出数组中的 K-or 值:基础位运算 力扣题目链接:https://leetcode.cn/problems/find-the-k-or-of-an-array/ 给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 nums 中的 K-or 是一个满足以下条件的非负整数: 只有…...

MySQL窗口函数:从理论到实践
目录 1. ROW_NUMBER() 2. RANK() 3. DENSE_RANK() 4. NTILE(n) 5. LAG() 和 LEAD() 6. FIRST_VALUE() 和 LAST_VALUE() 总结 MySQL中的窗口函数(Window Functions)允许用户对一个结果集的窗口(或分区)执行计算,…...

Vue+SpringBoot打造考研专业课程管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 考研高校模块2.3 高校教师管理模块2.4 考研专业模块2.5 考研政策模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 考研高校表3.2.2 高校教师表3.2.3 考研专业表3.2.4 考研政策表 四、系统展示五、核…...
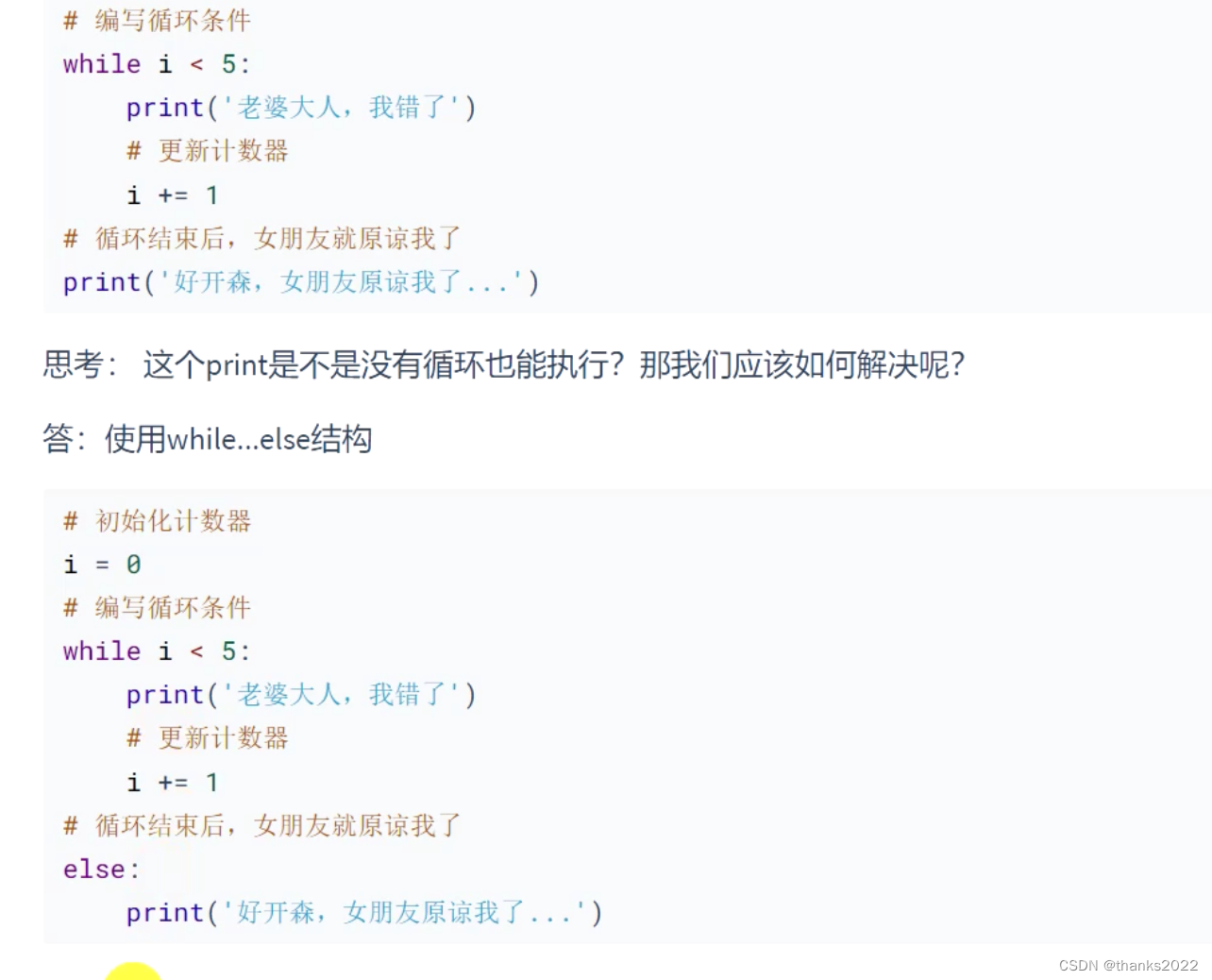
python基础第二天
世界杯小组赛成绩 注意: 1.循环 1.1while 1.2for 1.3 range 1.4 while else while 循环正常执行完才能执行else语句...

YOLOV9论文解读
代码:https://github.com/WongKinYiu/yolov9论文:https://arxiv.org/abs/2402.1361本文提出可编程梯度信息(PGI)和基于梯度路径规划的通用高效层聚合网络(GELAN),最终铸成YOLOv9目标检测全新工作!性能表现SOTA!在各个方…...

【Spring】21 通过@Primary注解优化注解驱动的自动装配
文章目录 Primary注解简介优势和适用场景小结 Spring 框架提供了强大的依赖注入机制,其中 Autowired 注解是一种常用的方式。然而,当存在多个候选 bean 时,通过类型自动装配可能导致选择困难。为了更好地控制这一过程,Spring 引入…...

【HTML】HTML基础7.3(自定义列表)
目录 标签 效果 代码 注意 标签 <dl> <dt>自定义标题</dt><dd>内容1</dd><dd>内容2</dd><dd>内容3</dd> 。。。。。。 </dl> 效果 代码 <dl><dt>蜘蛛侠系列</dt><dd>蜘蛛侠1</dd…...
)
java设计模式课后作业(待批改)
此文章仅记录学习,欢迎各位大佬探讨 实验(一) 面向对象设计 实验目的 ①使用类来封装对象的属性和功能; ②掌握类变量与实例变量,以及类方法与实例方法的区别; 知识回顾 详情见OOP课件 实验内容…...

qt 语音引擎 QTextToSpeech Microsoft SAPI
QT中语音播报的代码 在QT中实现语音播报可以使用QTextToSpeech类,具体代码如下: #include <QCoreApplication> #include <QTextToSpeech> #include <QDebug>int main(int argc, char *argv[]) {QCoreApplication a(argc, argv);// 创…...

react hook: useimperativeHandle
通过 useImperativeHandle,子组件可以选择性地暴露给父组件某些属性或方法,而不是将所有属性和方法暴露出去。 父组件 获得自组件的 ref,就能通过该 ref 来调用 focus来聚焦等功能 在 forwardRef 包装的组件中,ref 固定地是第二个…...
)
30天自制操作系统(第28天)
28.1 alloca __alloca 会在下述情况下被 C 语言的程序调用(采用 near-CALL 的方式)。 1、要执行的操作从栈中分配 EAX 个字节的内存空间( ESP - EAX; ) 2、要遵守的规则不能改变 ECX 、 EDX 、 EBX 、 EBP 、 ESI 、 EDI的值&am…...

Nginx启动服务
Nginx启动服务 一、启动前置 下载地址 如已安装Docker,下一步拉取Nginx最新的Docker镜像: docker pull nginx:latest查看拉取下来的镜像: docker images二、启动服务 创建Docker容器: docker run --name {projectname} -p 80…...
coqui-ai/TTS 案例model文件
GitHub - coqui-ai/TTS: 🐸💬 - a deep learning toolkit for Text-to-Speech, battle-tested in research and production Coqui AI的TTS是一款开源深度学习文本转语音工具,以高质量、多语言合成著称。它提供超过1100种语言的预训练模型库&…...

如何利用API接口进行高效的商品变体管理?
要利用API接口进行高效的商品变体管理,您需要执行一系列策略和技术步骤来确保数据的准确性和实时性。以下是详细的指南: 1. 确定变体管理需求 分析产品:识别具有变体的产品,并明确这些变体的属性(如尺寸、颜色、材质…...
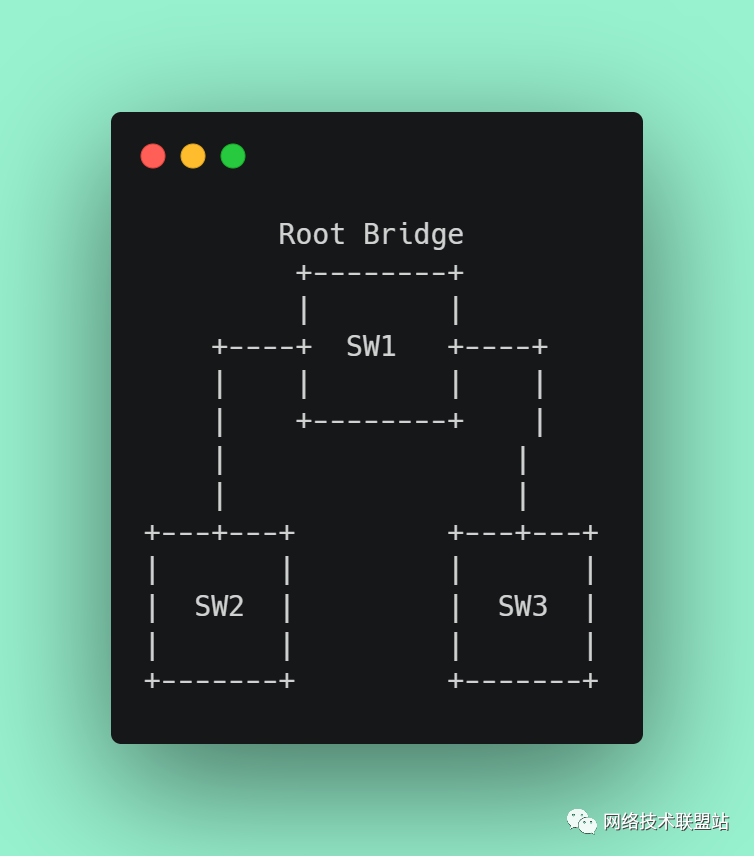
扼杀网络中的环路:STP、RSTP、MSTP
目录 前言: 一、STP(Spanning Tree Protocol) 1.1 STP功能 1.2 STP应用 二、RSTP(Rapid Spanning Tree Protocol) 2.1 RSTP功能 2.2 RSTP应用 三、MSTP(Multiple Spanning Tree Protocol࿰…...

青少年如何从零开始学习Python编程?有它就够了!
文章目录 写在前面青少年为什么要学习编程 推荐图书图书特色内容简介 推荐理由粉丝福利写在最后 写在前面 本期博主给大家带来一本非常适合青少年学习编程的图书,快来看看吧~ 青少年为什么要学习编程 青少年学习编程,就好比在他们年轻时就开始掌握一种…...
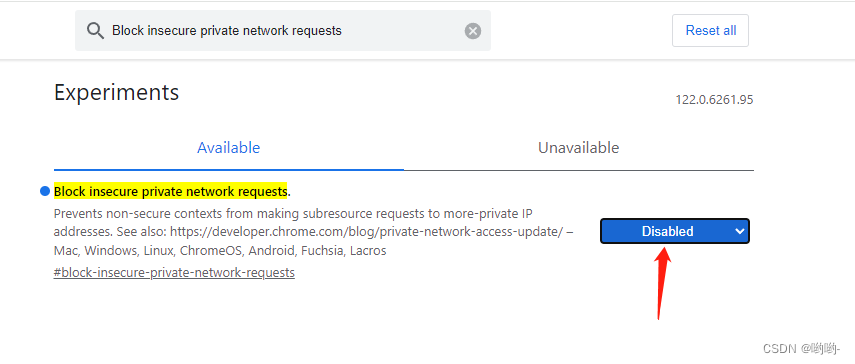
触发HTTP preflight预检及跨域的处理方法
最近在做需求的过程中,遇到了很多跨域和HTTP预检的问题。下面对我所遇到过的HTTP preflight和跨域的相关问题进行总结: 哪些情况会触发HTTP preflight preflight属于cors规范的一部分,在有跨域的时候,在一定情况下会触发preflig…...

【算法可视化】搜索算法专题
运行平台 Algorithm Visualizer 选数 [NOIP2002 普及组] 选数 // 导入可视化库 { const { Tracer, Array1DTracer, LogTracer, Layout, VerticalLayout } require(algorithm-visualizer); // }const N 4, K 3; //从包含4个元素的集合中选出3个数 let ans 0 //方案数 co…...
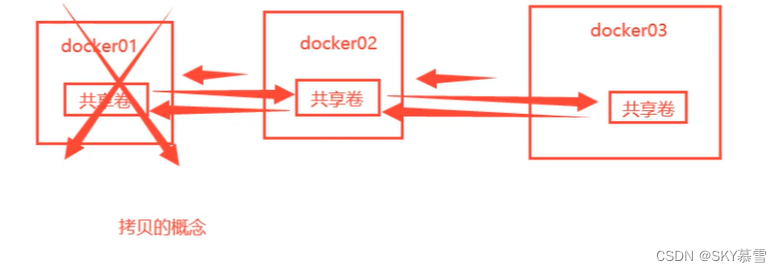
编写dockerfile挂载卷、数据容器卷
编写dockerfile挂载卷 编写dockerfile文件 [rootwq docker-test-volume]# vim dockerfile1 [rootwq docker-test-volume]# cat dockerfile1 FROM centosVOLUME ["volume01","volume02"]CMD echo "------end------" CMD /bin/bash [rootwq dock…...

理解OAuth 2.0
OAuth是一个关于授权(authorization)的开放网络标准,在全世界得到广泛应用,目前的版本是2.0版。 本文对OAuth 2.0的设计思路和运行流程,做一个简明通俗的解释,主要参考材料为RFC 6749。 一、应用场景 为了…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
