堆和堆排序
堆排序是一种与插入排序和并归排序十分不同的算法。
优先级队列
Priority Queue
优先级队列是类似于常规队列或堆栈数据结构的抽象数据类型(ADT)。优先级队列中的每个元素都有一个相关联的优先级key。在优先级队列中,高优先级的元素优先于低优先级的元素。
虽然优先级队列通常使用堆heap实现,但它们在概念上与堆不同。优先级队列是一种抽象的数据结构,如列表或映射; 正如列表可以用链表或数组实现一样,优先级队列也可以用堆或其他方法(如有序数组)实现。
堆
Heap
堆可以理解为由一个由数组来顺序存储的完全二叉树。
最大堆:任意节点的key ≥ 子节点的key
类似的
最小堆:任意节点的key ≤ 子节点的key
以最大堆为例,来讲解
最大堆
最大堆的操作
build_max_heap:根据一个未排序的数组生成一个最大堆
max_heapify: 如果子树的根节点违反最大堆的特性,就对其进行纠正。max_heapify的前提是子树的左右子树都是最大堆。
build_max_heap的伪代码:
for i = n/2 down to 1do max_heapify(A,i)max_heapify和build_max_heap的时间复杂度
对叶子结点上面一层的结点(level 1)进行max_heapify是O(1)的时间复杂度
对叶子结点上面i层 level i 的结点进行max_heapify是O(i)
n/4个结点是level 1,n/8个结点是level 2,n/16个结点是level 3 ... 1个结点是level logn
因此max_heapify的时间复杂度为O(logn),可计算出build_max_heap的时间复杂度为O(n)
计算过程在最底下
堆排序步骤
1.根据一个未排序的数组来创建最大堆
2.找到最大元素A[1]
3.交换元素A[n]和A[1],现在最大元素位于堆的尾部
4.移除A[n](最大元素),只需将存放堆的数组的大小减1
5.经过交换元素之后的堆也许违背了最大堆的定义,但是A[1]的孩子仍然是最大堆,因此进行max_heapify,经过修正后,整个堆就是最大堆;重复步骤2-5,n次。
class Solution {
public://堆是一个完全二叉树,因此适合使用顺序存储的方式。//堆排序步骤://1.根据一个未排序的数组来创建最大堆//2.找到最大元素A[1]//3.交换元素A[n]和A[1],现在最大元素位于堆的尾部//4.移除A[n](最大元素),存放堆的数组的大小减1//5.经过交换元素之后的堆也许违背了最大堆的定义,但是A[1]的孩子仍然是最大堆,因此进行max_heapify,经过修正后,整个堆就是最大堆;重复2-5,n次//时间复杂度O(nlogn)vector<int> sortArray(vector<int>& nums) {build_max_heap(nums);//堆排序int n = nums.size();while(n > 0){//重复n次//找到最大元素,并与堆末尾元素进行交换int max_elem = nums[0];nums[0] = nums[n-1];nums[n-1] = max_elem;--n;//移出末尾元素//进行max_heapifymax_heapify(nums, 0, n);}return nums;}void build_max_heap(vector<int>& nums){int size = nums.size();for(int i = size/2-1;i >= 0;--i){max_heapify(nums, i, size);}}void max_heapify(vector<int>& nums, int i, int size){//将A[i]修正为最大堆//A[i]的左孩子为A[2i+1],右孩子为A[2i+2]int left = (i<<1) + 1;int right = left + 1;int large = left;//默认较大元素为左节点while(large < size){if(right < size && nums[right] > nums[left]){//假如右结点大于左节点large = right;//记右结点为较大的}if(nums[i] < nums[large]){//假如父节点小于左右结点中较大的结点//将父节点与较大的结点进行交换,从而使父节点大于左右子结点,符合最大堆的约束int tmp = nums[i];nums[i] = nums[large];nums[large] = tmp;i = large;//i调节为其子结点largelarge = (i<<1)+ 1;//large调整为i的左子节点}else{break;}}}};


相关文章:

堆和堆排序
堆排序是一种与插入排序和并归排序十分不同的算法。 优先级队列 Priority Queue 优先级队列是类似于常规队列或堆栈数据结构的抽象数据类型(ADT)。优先级队列中的每个元素都有一个相关联的优先级key。在优先级队列中,高优先级的元素优先于…...
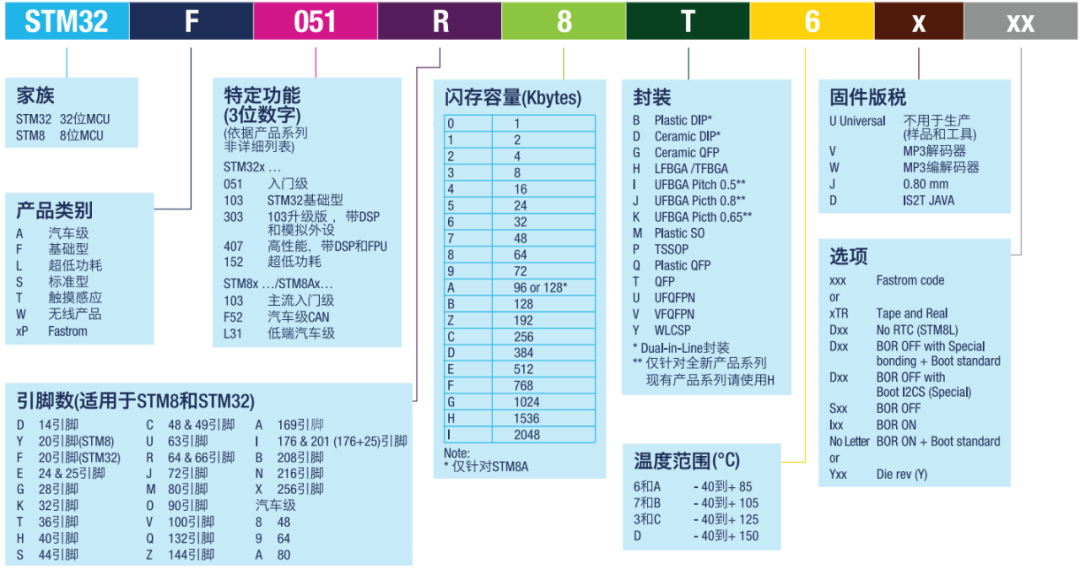
STM32 | 零基础 STM32 第一天
零基础 STM32 第一天 一、认知STM32 1、STM32概念 STM32:意法半导体基于ARM公司的Cortex-M内核开发的32位的高性能、低功耗单片机。 ST:意法半导体 M:基于ARM公司的Cortex-M内核的高性能、低功耗单片机 32:32位单片机 2、STM32开发的产品 STM32开发的产品&a…...
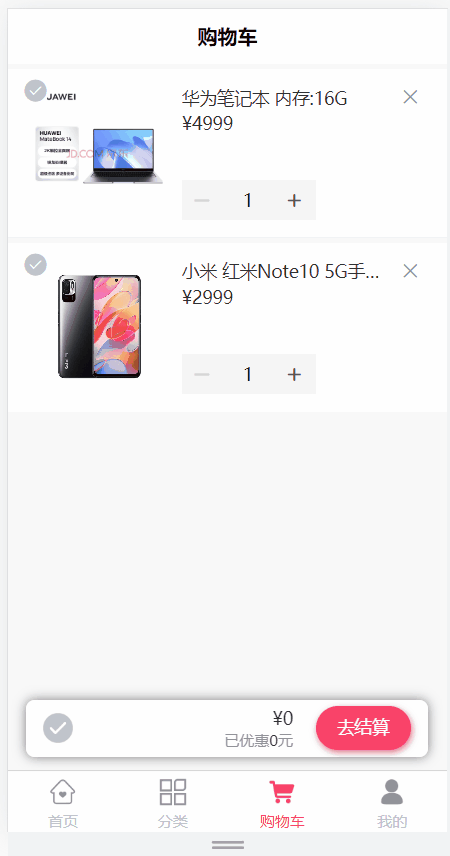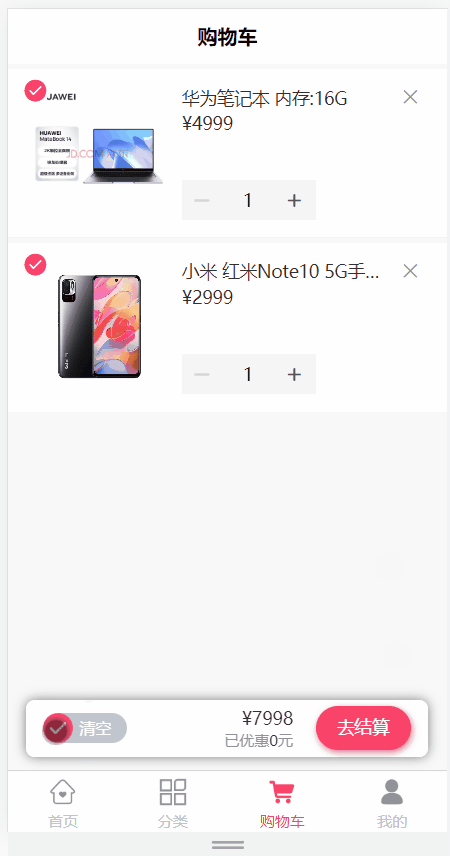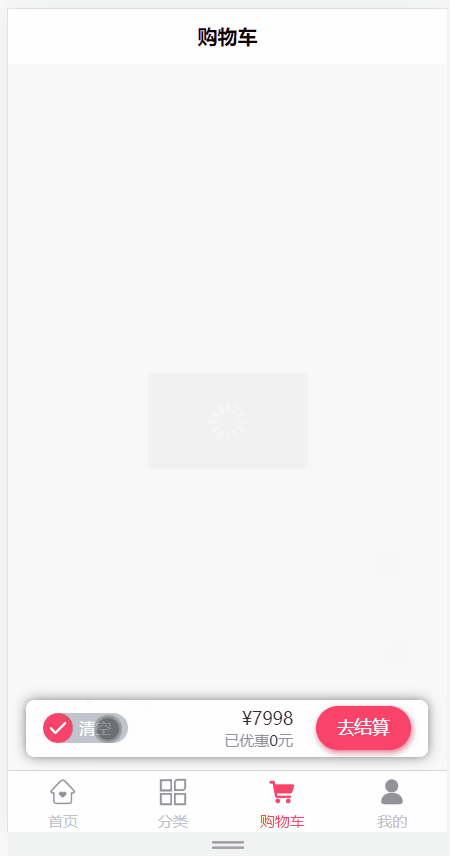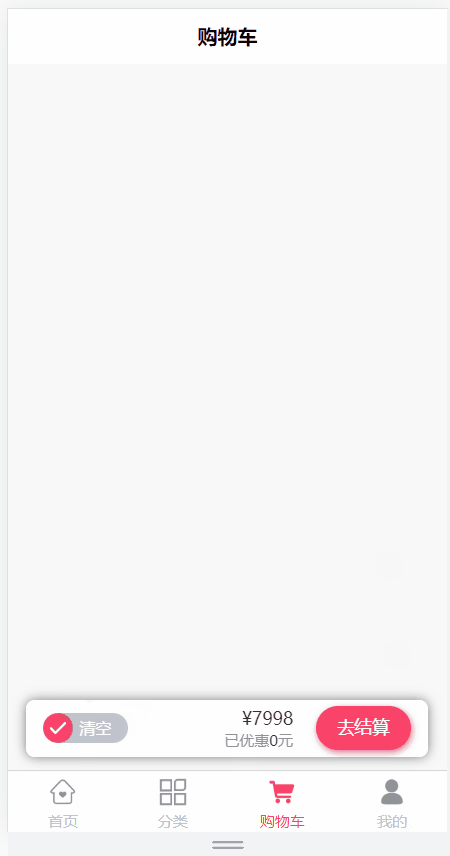
day16_购物车(添加购物车,购物车列表查询,删除购物车商品,更新选中商品状态,完成购物车商品的全选,清空购物车)
文章目录 购物车模块1 需求说明2 环境搭建3 添加购物车3.1 需求说明3.2 远程调用接口开发3.2.1 ProductController3.2.2 ProductService 3.3 openFeign接口定义3.3.1 环境搭建3.3.2 接口定义3.3.3 降级类定义 3.4 业务后端接口开发3.4.1 添加依赖3.4.2 修改启动类3.4.3 CartInf…...
基于Spring Boot的图书个性化推荐系统 ,计算机毕业设计(带源码+论文)
源码获取地址: 码呢-一个专注于技术分享的博客平台一个专注于技术分享的博客平台,大家以共同学习,乐于分享,拥抱开源的价值观进行学习交流http://www.xmbiao.cn/resource-details/1765769136268455938...
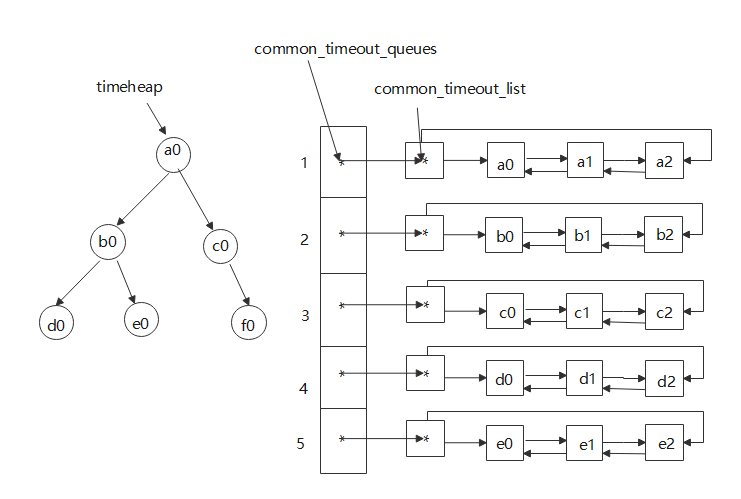
libevent源码解析:定时器事件(三)
文章目录 前言一、用例小根堆管理定时器事件小根堆和链表管理定时器事件区别 二、基本数据结构介绍结构体成员分析小根堆和链表common_timeout图示 三、源码分析小根堆管理定时器事件event_newevent_addevent_dispatch 链表common_timeout管理定时器事件event_base_init_common…...
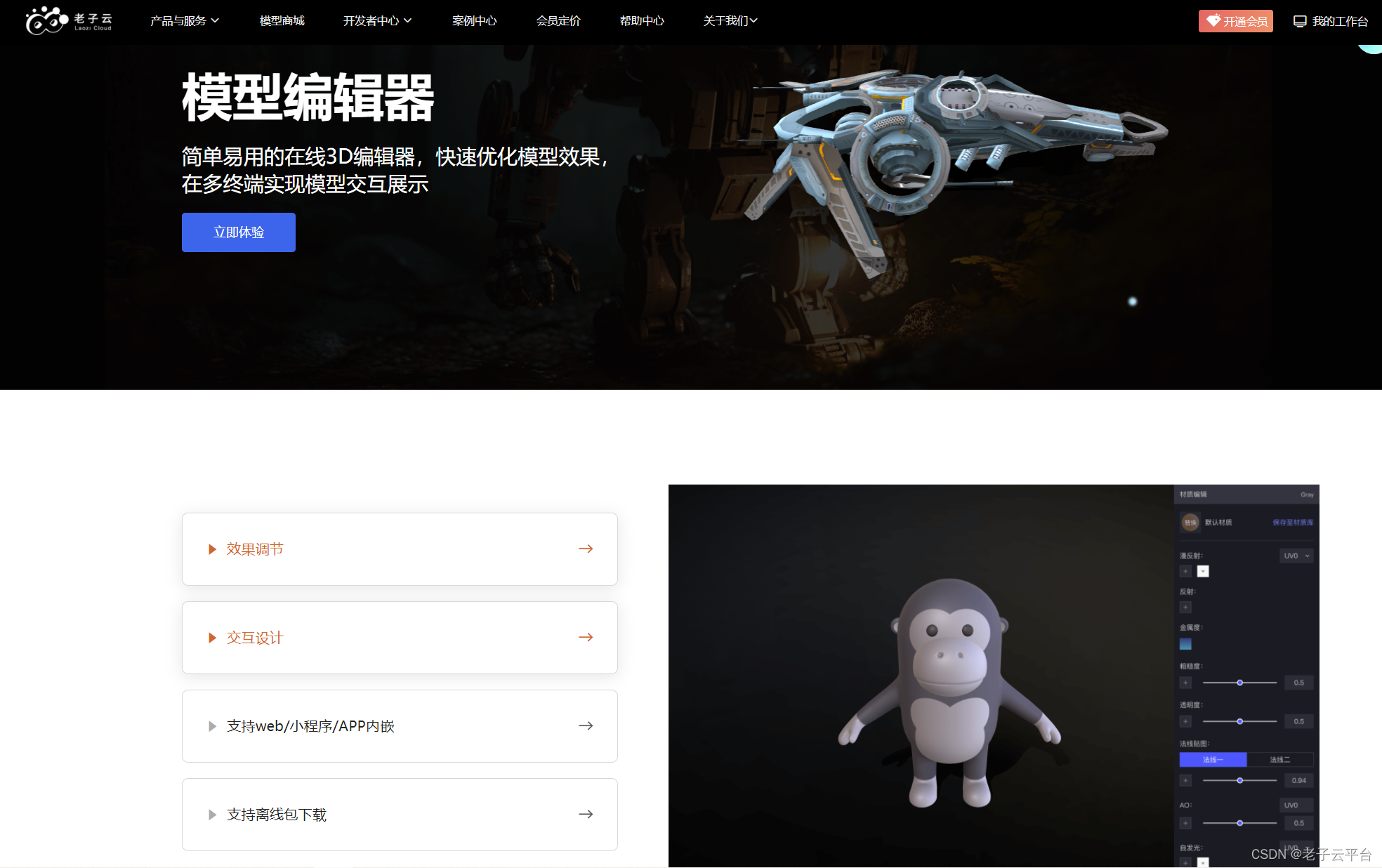
3D资产管理
3D 资产管理是指组织、跟踪、优化和分发 3D 模型和资产以用于游戏、电影、AR/VR 体验等各种应用的过程。 3D资产管理也称为3D内容管理。 随着游戏、电影、建筑、工程等行业中 3D 内容的增长,实施有效的资产管理工作流程对于提高生产力、减少错误、简化工作流程以及使…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Blank)
空白填充组件,在容器主轴方向上,空白填充组件具有自动填充容器空余部分的能力。仅当父组件为Row/Column/Flex时生效。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件…...
【手游联运平台搭建】游戏平台的作用
随着科技的不断发展,游戏行业也在不断壮大,而游戏平台作为连接玩家与游戏的桥梁,发挥着越来越重要的作用。游戏平台不仅为玩家提供了便捷的游戏体验,还为游戏开发者提供了广阔的市场和推广渠道。本文将从多个方面探讨游戏平台的作…...

手把手教会你 - StreamAPI基本用法
1. 简介 目前响应式编程的学习中很多时候都用到了Lambda表达式和StreamAPI,那么今天就在这里记录一下一些最基本的使用方法。 StreamAPI中引入了流的概念,其将集合看作一种流,流在管道中传输(动态的),可以…...

和为K的子数组
题目: 使用前缀和的方法可以解决这个问题,因为我们需要找到和为k的连续子数组的个数。通过计算前缀和,我们可以将问题转化为求解两个前缀和之差等于k的情况。 假设数组的前缀和数组为prefixSum,其中prefixSum[i]表示从数组起始位…...
Redis:java中redis的基本使用(springboot)
文章目录 springboot中使用redisspringboot 连接 redis三种方式导入依赖增删改查小练习 springboot中使用redis springboot 连接 redis三种方式 jedis (redis官方提供的)springboot自带的redisson (基于jedis优化的,性能最好,使…...

微型计算机技术
摘要:微型计算机是通用计算机的一个重要发展分支,自1981年美国IBM公司推出第一代商用微型计算机以来,微型计算机迅速进入社会各个领域,且技术不断更新、产品快速换代,已成为人们工作和生活中不可缺少的基本工具。 一、微型计算机技术发展历史 1.第一代微处理器(19…...
mysql下载教程
什么是mysql MySQL是一种开源的关系型数据库管理系统,由瑞典MySQL AB公司开发,现在由Oracle公司维护。MySQL支持多个操作系统,包括Linux、Windows、macOS等。它是一种客户端/服务器模式的数据库,提供高效、可靠、稳定的数据存储和…...
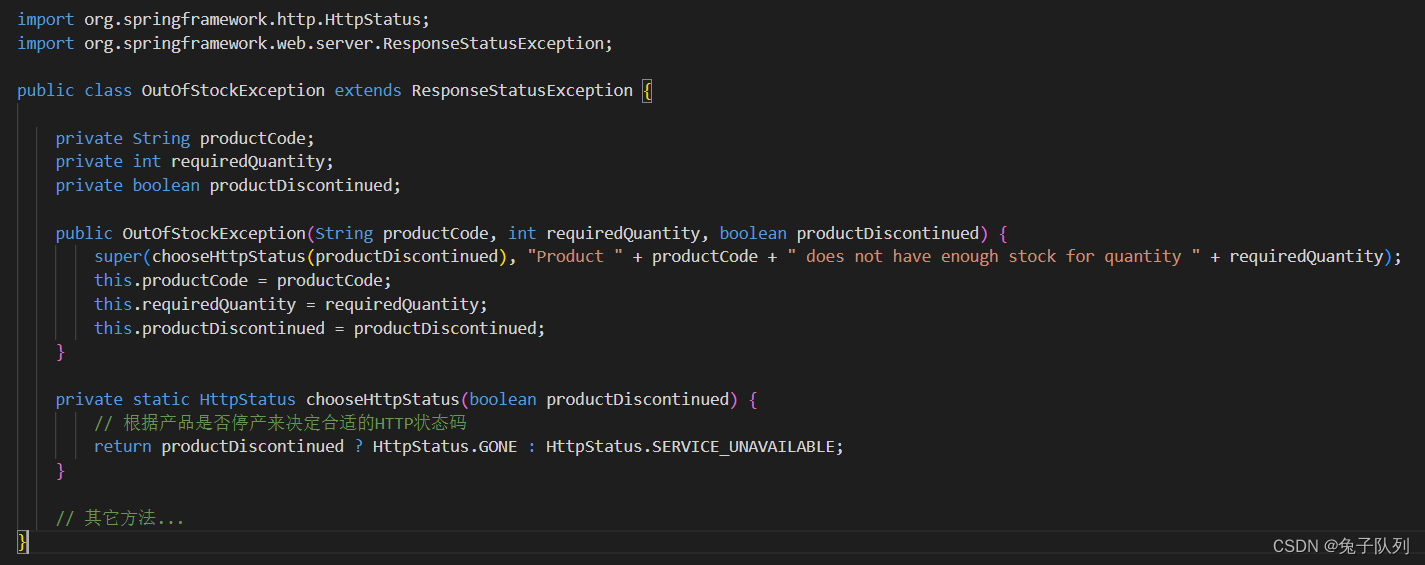
ResponseStatusException
目录 概述: 综合实例: 继承 ResponseStatusException-自定义异常类 继承 ResponseStatusException-自定义响应头信息 继承 ResponseStatusException-定制更多异常处理逻辑 继承 ResponseStatusException-根据异常发生的上下文动态改变 HTTP 状态码…...
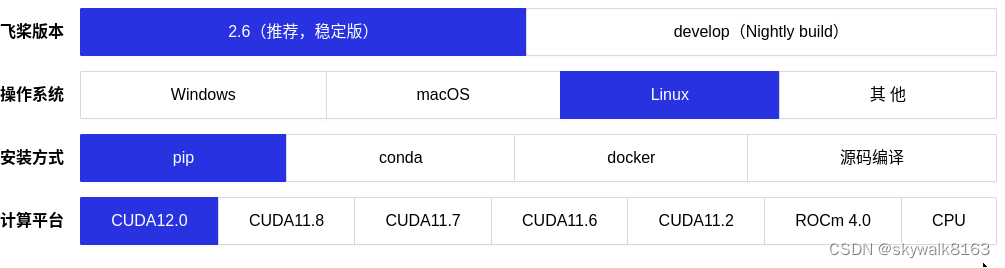
第五十二回 戴宗二取公孙胜 李逵独劈罗真人-飞桨AI框架安装和使用示例
吴用说只有公孙胜可以破法术,于是宋江请戴宗和李逵去蓟州。两人听说公孙胜的师傅罗真人在九宫县二仙山讲经,于是到了二仙山,并在山下找到了公孙胜的家。 两人请公孙胜去帮助打高唐州,公孙胜说听师傅的。罗真人说出家人不管闲事&a…...

CSAPP-程序的机器级表示
文章目录 概念扫盲思想理解经典好图安全事件 概念扫盲 1.汇编代码使用文本格式,相较于汇编的二进制可读性更好 2.程序内存包括:可执行的机器代码、操作系统需要的信息、管理过程调用和返回的运行时栈、用户分配的内存块 3.链接器为函数调用找到匹配的可…...
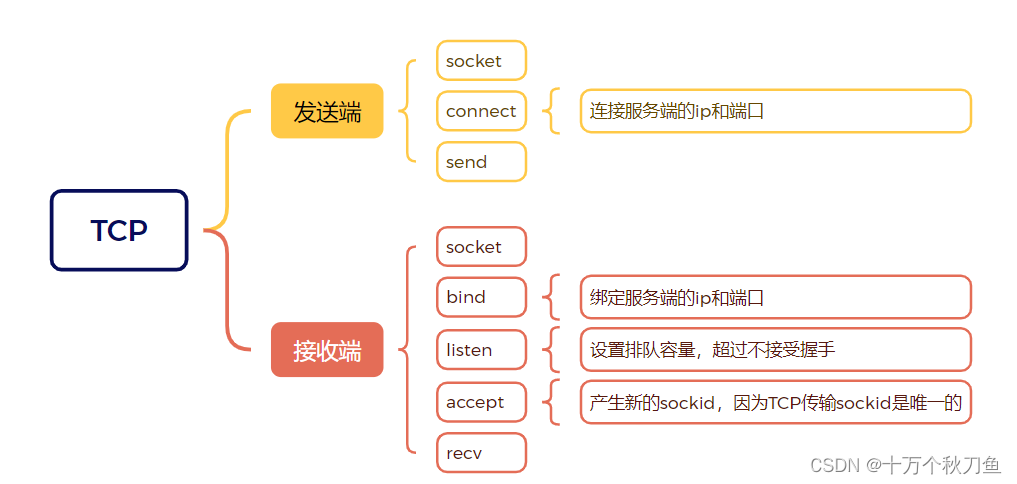
TCP传输收发
TCP通信: TCP发端: socket connect send recv close TCP收端: socket bind listen accept send recv close 1.connect int connect(int sockfd, const struct sockaddr *addr, socklen_t ad…...

OJ习题之——圆括号编码
圆括号编码 1.题目描述2.完整代码3.图例演示 1.题目描述 题目描述 令Ss1 s2 …sn是一个规则的圆括号字符串。S以2种不同形式编码: (1)用一个整数序列Pp1 p2 … pn编码,pi代表在S中第i个右圆括号的左圆括号数量。(记为…...
Android耗电分析之Battery Historian工具使用
Battery-Historian是谷歌推出的一款专门分析Bugreport的工具,是谷歌在2015年I/O大会上推出的一款检测运行在android5.0(Lollipop)及以后版本的设备上电池的相关信息和事件的工具,是一款对于分析手机状态,历史运行情况很好的可视化分析工具。 …...

vue el-avatar 使用require提示无法找到图片
报错信息 错误代码 问题分析 vue初始化DOM树时没有挂载数据,导致无法找到模块 解决方案...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
