代码随想录算法训练营第五十五天|583. 两个字符串的删除操作、72. 编辑距离。
583. 两个字符串的删除操作
题目链接:两个字符串的删除操作
题目描述:
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
解题思路:
1、确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
2、确定递推公式
当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
3、dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
dp[0][j]的话同理
代码实现:
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1 + 1][len2 + 1];for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return len1 + len2 - dp[len1][len2] * 2;}
}
72. 编辑距离
题目链接:编辑距离
题目描述:
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
解题思路:
递推公式:
1、if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
2、if (word1[i - 1] != word2[j - 1]),此时就需要编辑了。
操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] = = word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
代码实现:
class Solution {public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];// 初始化for (int i = 1; i <= m; i++) {dp[i][0] = i;}for (int j = 1; j <= n; j++) {dp[0][j] = j;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 因为dp数组有效位从1开始// 所以当前遍历到的字符串的位置为i-1 | j-1if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;}}}return dp[m][n];}
}
相关文章:

代码随想录算法训练营第五十五天|583. 两个字符串的删除操作、72. 编辑距离。
583. 两个字符串的删除操作 题目链接:两个字符串的删除操作 题目描述: 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 解题思路: 1、确定dp数组&#x…...
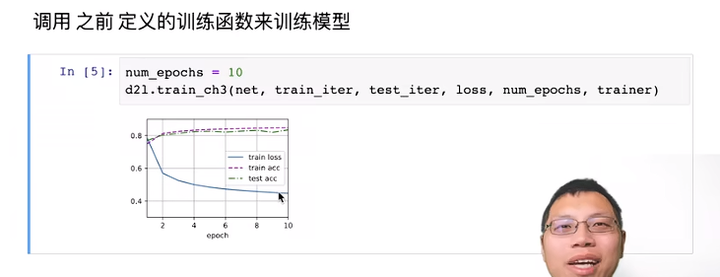
Softmax 回归 + 损失函数 + 图片分类数据集【动手学深度学习v2】李沐动手学深度学习课程笔记
目录 Softmax回归 损失函数 图片分类数据集 Softmax回归从零开始实现 Softmax回归简洁实现 Softmax回归 回归和分类的区别 回归问题举例上节课的预测房价问题,分类问题就是对样本进行分类 回归和分类的具体区别 假设真实的类别为第i个类别(值为1&#x…...

git 初始化项目并上传到github
如果还没配置过,需要配置账号信息 git config --global user.name "baymax-collab" git config --global user.email "baymax-collabtest.com"创建一个新的存储库 git clone gitgithub.com:xxxx cd test git switch --create main touch READ…...
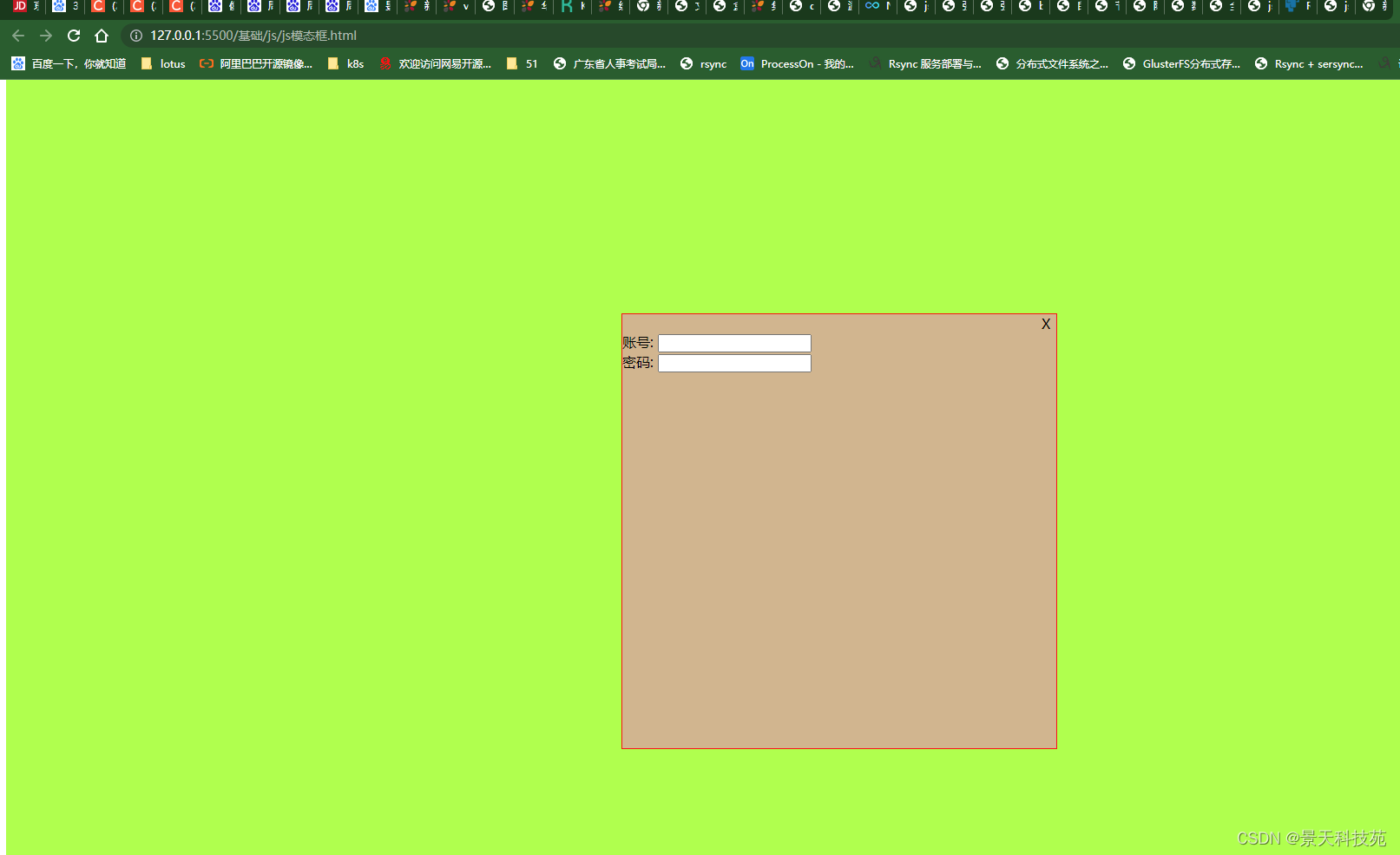
前端javascript的DOM对象操作技巧,全场景解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 所属的专栏:前端泛海 景天的主页:景天科技苑 文章目录 1.js的DOM介绍2.节点元素层级关系3.通过js修改,清空节点…...
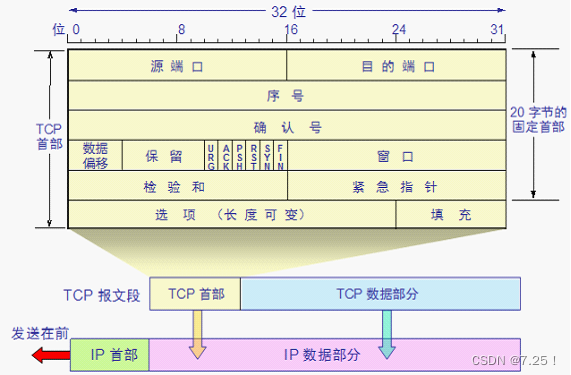
TCP包头、TCP为什么安全可靠、UDP和TCP的区别、http协议
我要成为嵌入式高手之3月8日Linux高编第十八天!! __________________________________________________ 学习笔记 TPC包头 1、序号 发送端发送数据包的编号 2、确认号 已经确认接收到的数据的编号,只有当ACK为1时,该位才有用 …...
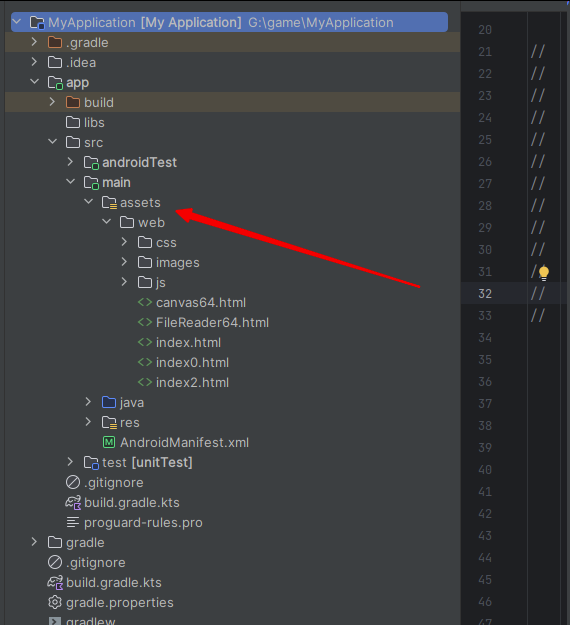
Android使用WebView打开内嵌H5网页
Android打开外部网页链接请参考上一篇文章 https://public.blog.csdn.net/article/details/136384559 继上篇,新建assets文章夹,将H5的网页资源放到此文件夹下 把H5的资源文件都拷进来 这个时候,将添加打开本地网页的代码: //打…...
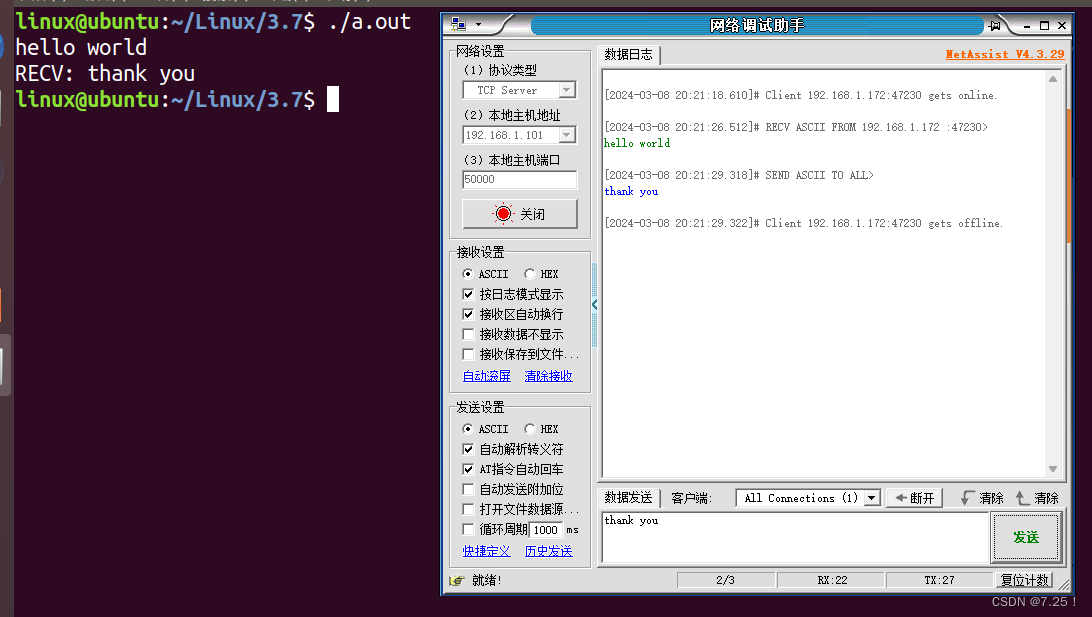
UDP实现文件的发送、UDP实现全双工的聊天、TCP通信协议
我要成为嵌入式高手之3月7日Linux高编第十七天!! ———————————————————————————— 回顾 重要程序 1、UDP实现文件的发送 发端: #include "head.h"int main(void) {int sockfd 0;struct sockaddr_i…...

Yocto - Project Quick Build
欢迎光临! 这篇简短的文档将向您介绍使用 Yocto 项目构建典型镜像的过程。本文还介绍了如何为特定硬件配置构建。您将使用 Yocto Project 构建一个名为 Poky 的参考嵌入式操作系统。 Welcome! This short document steps you through the process for a typical i…...
)
深入探讨C++中的可变参数列表(Variadic Templates)
文章目录 导言可变参数列表的基本用法使用std::initializer_list应用场景 导言 在C编程中,处理可变数量参数的能力是一种非常有用的功能。通过可变参数列表,你可以编写更加通用和灵活的函数,从而提高代码的可读性和重用性。本文将详细介绍C中…...

MS2548 国产自动方向控制、半双工 RS-485 收发器 替代MAX13487
MS2548 国产自动方向控制、半双工 RS-485 收发器 替代MAX13487 北京冠宇铭通科技有限公司 肖小姐 产品简述 MS2548 是一个 5V 供电、半双工 RS-485 收发器。 芯片具有自动换向控制功能,可用于隔离485 端口,驱动器输入与使能信号一起配合控制芯片的状态&…...
数据库大师之路:Oracle在线学习平台全指南!
介绍数据库是由甲骨文公司开发的一款关系数据库管理系统(RDBMS),在数据库领域具有领先地位,并且以其系统可移植性而闻名。以下是对Oracle数据库的详细介绍: 市场地位:Oracle数据库是目前世界上流行的关系数…...
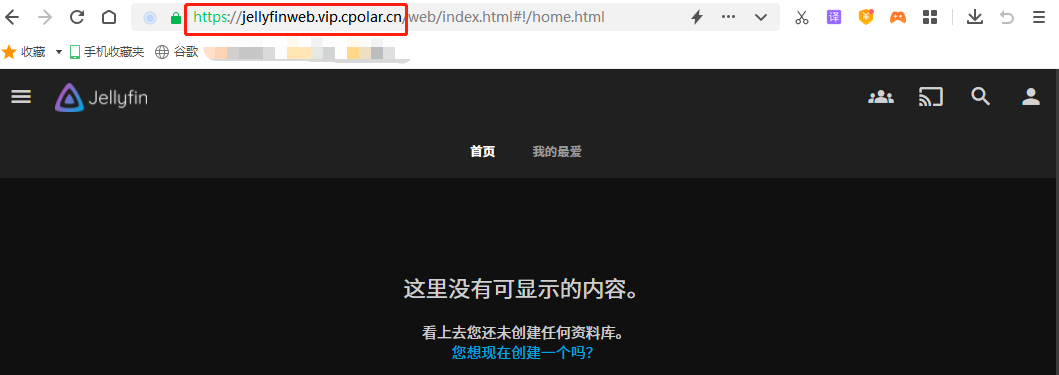
如何在Windows系统部署Jellyfin Server并实现公网访问内网影音文件
文章目录 1. 前言2. Jellyfin服务网站搭建2.1. Jellyfin下载和安装2.2. Jellyfin网页测试 3.本地网页发布3.1 cpolar的安装和注册3.2 Cpolar云端设置3.3 Cpolar本地设置 4.公网访问测试5. 结语 1. 前言 随着移动智能设备的普及,各种各样的使用需求也被开发出来&…...
CORBA协议开发)
华为北向网管NCE开发教程(3)CORBA协议开发
华为北向网管NCE开发教程(1)闭坑选接口协议 华为北向网管NCE开发教程(2)REST接口开发 华为北向网管NCE开发教程(3)CORBA协议开发 如果你真的还有选择的余地,能用REST,尽量用REST&…...
)
【算法训练营】最长公共子序列,倒水问题,奶牛吃草(Python实现)
最长公共子序列 时间限制:1 sec 空间限制:256 MB 问题描述 给定两个 1 到 n 的排列 A,B (即长度为 n 的序列,其中 [1,n] 之间的所有数都出现了恰好一次)。 求它们的最长公共子序列长度。 输入格式 第一行一个整数 n &a…...

Armadillo:矩阵类、向量类、Cube类和泛型类
文章目录 矩阵类、向量类、Cube类和泛型类Mat<type>matcx_matCol<type>veccx_vecRow<type>rowveccx_rowvecCube<type>cubecx_cubefield<object_type>SpMat<type>sp_matsp_cx_mat运算符: − * % / ! < > <…...

【守护健康】小脑萎缩患者必备营养指南
当生活给予我们挑战,我们选择用科学和关爱予以回应。面对小脑萎缩这一难题,正确的营养补充不仅是一剂强心针,更是患者康复之路上的坚实伙伴。今天,让我们一起了解那些能够助力小脑萎缩患者的神奇维生素! 1. 维生素B群…...
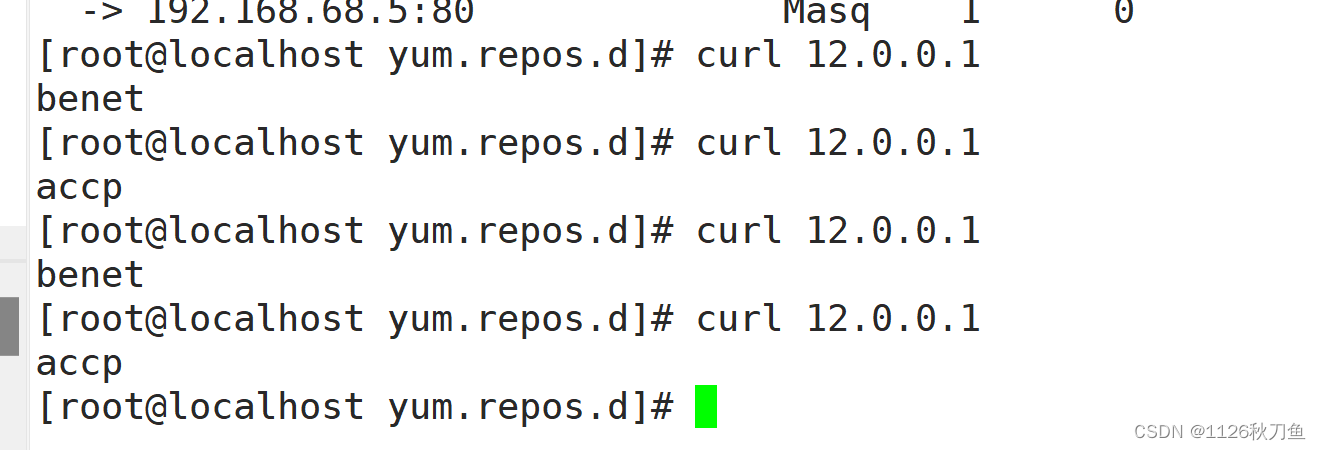
lvs集群中NAT模式
群集的含义 由多台主机构成,但对外表现为一个整体,只提供一个访问入口,相当于一台大型的计算机。 横向发展:放更多的服务器,有调度分配的问题。 垂直发展:升级单机的硬件设备,提高单个服务器自身功能。 …...
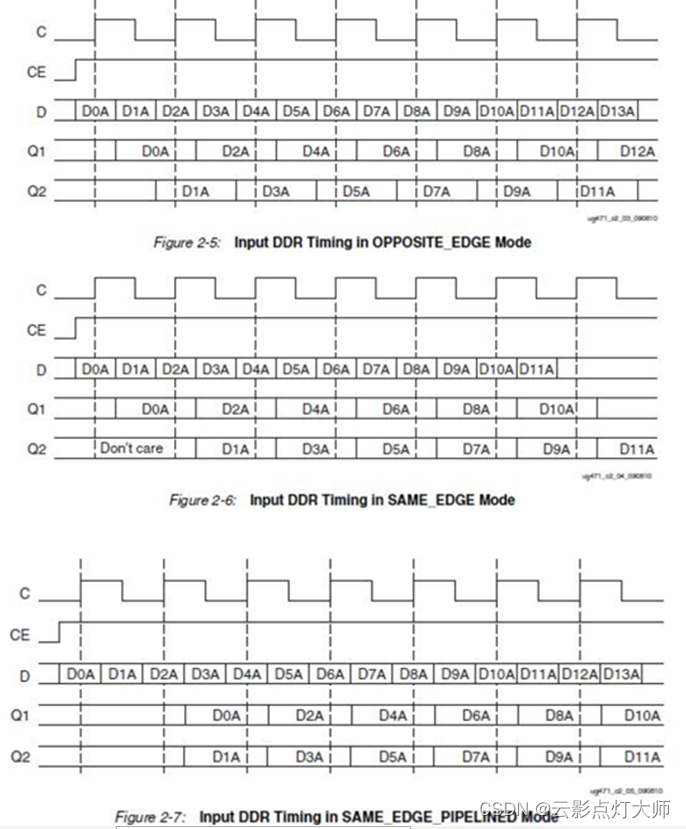
FPGA——三速自适应以太网设计(2)GMII与RGMII接口
FPGA——以太网设计(2)GMII与RGMII 基础知识(1)GMII(2)RGMII(3)IDDR GMII设计转RGMII接口跨时钟传输模块 基础知识 (1)GMII GMII:发送端时钟由MAC端提供 下…...
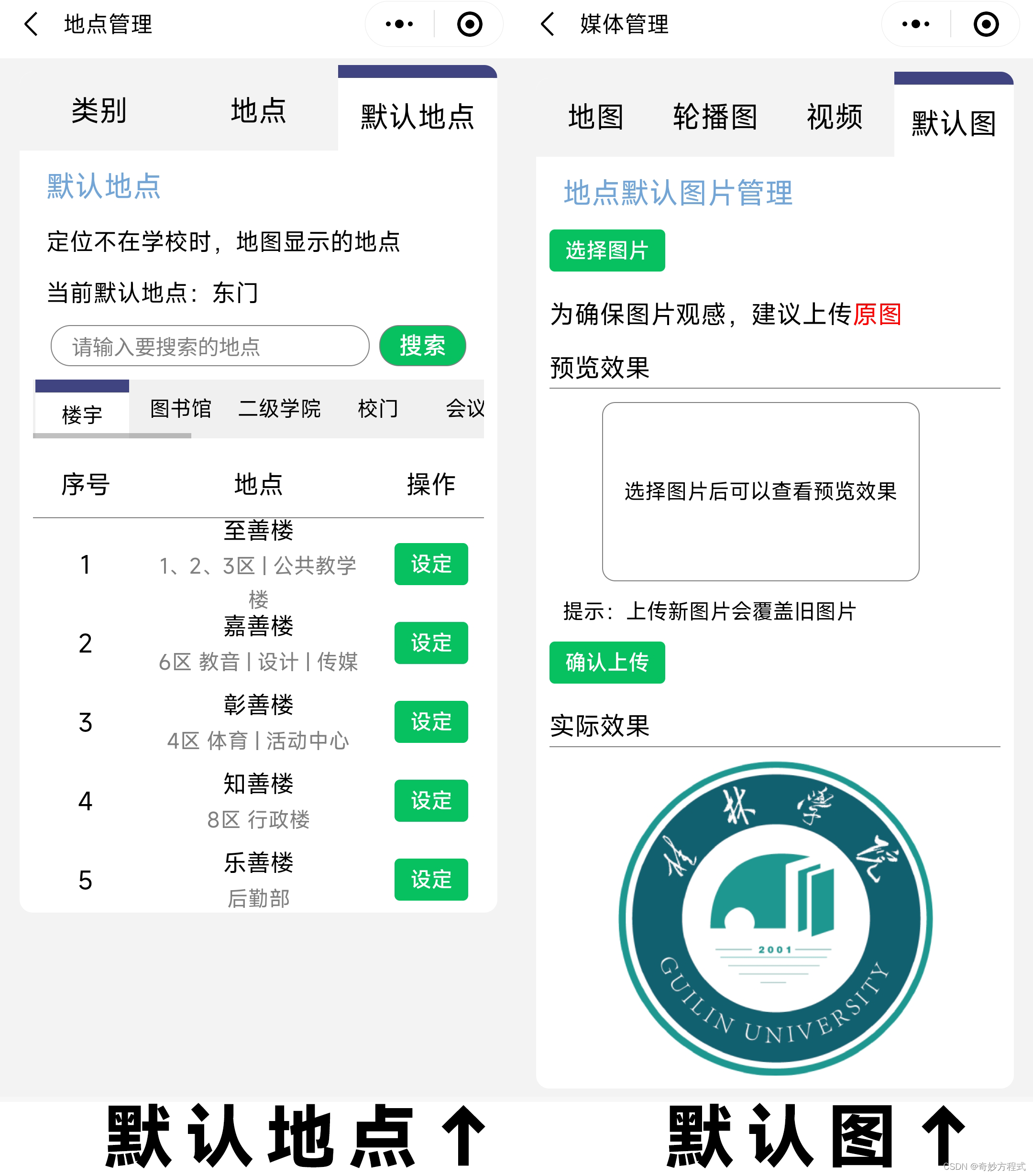
【校园导航小程序】2.0版本 静态/云开发项目 升级日志
演示视频 【校园导航小程序】2.0版本 静态/云开发项目 演示 首页 重做了首页,界面更加高效和美观 校园指南页 新增了 “校园指南” 功能,可以搜索和浏览校园生活指南 地图页 ①弃用路线规划插件,改用SDK开发包。可以无阻通过审核并发布…...
)
深入揭秘Lucene:全面解析其原理与应用场景(二)
本系列文章简介: 本系列文章将深入揭秘Lucene,全面解析其原理与应用场景。我们将从Lucene的基本概念和核心组件开始,逐步介绍Lucene的索引原理、搜索算法以及性能优化策略。通过阅读本文,读者将会对Lucene的工作原理有更深入的了解…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
