用A*算法求解八数码问题
用A*算法求解八数码问题
- 实现两种启发函数
- 实现A*算法
- 测试
实现两种启发函数
采取两种策略实现启发函数:
- 策略1:不在目标位置的数字个数
- 策略2:曼哈顿距离(将数字直接移动到对应位置的步数总数)
# 策略1: 不在目标位置的数字个数,即 state 与 goal_state 不相同的数字个数
def h1(state, goal_state):'''state, goal_state - 3x3 list'''distance = 0for i in range(3):for j in range(3):if state[i][j] != goal_state[i][j] and state[i][j] != 0:distance += 1return distance# 功能性函数,用于查找给定数字 num 在 goal_state 中的坐标
def find_num(num, goal_state):for i in range(3):for j in range(3):if goal_state[i][j] == num:return i, jreturn -1, -1# 策略2: 曼哈顿距离之和
def h2(state, goal_state):'''state, goal_state - 3x3 list'''distance = 0for i in range(3):for j in range(3):if state[i][j] == 0:continueif state[i][j] == goal_state[i][j]:continuegoal_i, goal_j = find_num(state[i][j], goal_state)distance += abs(i - goal_i) + abs(j - goal_j)return distance# 测试
start_state = [[2, 8, 3],[1, 6, 4],[7, 0, 5]
]goal_state = [[1, 2, 3],[8, 0, 4],[7, 6, 5]
]# 不在目标位置的数字:1、2、8、6,共 4 个
# 1 需移动 1 步到达正确位置
# 2 需移动 1 步到达正确位置
# 8 需移动 2 步到达正确位置
# 6 需移动 1 步到达正确位置
# 曼哈顿距离共 5 步print(h1(start_state, goal_state)) # 4
print(h2(start_state, goal_state)) # 5
实现A*算法
为了便于替换启发函数,将其作为参数传入函数:
# 定义A*算法函数
def astar(start_state, goal_state, h):'''params:start_state - 3x3 list 初始状态goal_state - 3x3 list 目标状态h - function 启发函数returns:expanded_nodes - 扩展节点数run_time - 算法运行时间path - 算法运行路径ps. 当路径不存在时,会返回 run_time = 0, path = None'''start_time = time.time() # 算法开始open_list = [(h(start_state, goal_state), start_state)] # 存储待扩展的节点的优先队列closed_set = set() # 存储已经扩展过的节点的集合came_from = {} # 记录节点之间的关系,即每个节点的父节点是哪个节点expanded_nodes = 0 # 记录扩展节点的数量while open_list: # 带扩展节点队列不为空_, current_state = heapq.heappop(open_list) # 弹出优先级最高的节点expanded_nodes += 1if current_state == goal_state: # 找到目标状态# 回溯路径path = [current_state]while tuple(map(tuple, current_state)) in came_from:current_state = came_from[tuple(map(tuple, current_state))]path.append(current_state)end_time = time.time() # 记录算法结束时间return expanded_nodes, end_time-start_time, path[::-1]closed_set.add(tuple(map(tuple, current_state))) # 将当前节点状态加入已扩展节点集合zero_i, zero_j = find_num(0, current_state) # 找到当前的空格坐标moves = [(0, 1), (0, -1), (1, 0), (-1, 0)] # 四周的格子for di, dj in moves:new_i, new_j = zero_i + di, zero_j + dj # 移动的数字if 0 <= new_i < 3 and 0 <= new_j < 3: # 确保新位置在范围内new_state = [row[:] for row in current_state] # 拷贝 current_statenew_state[zero_i][zero_j], new_state[new_i][new_j] = current_state[new_i][new_j], current_state[zero_i][zero_j] # 移动空白格if tuple(map(tuple, new_state)) in closed_set:continue # 如果新状态已经扩展过,则跳过new_cost = len(came_from) + 1 + h(new_state, goal_state) # 计算新状态的代价heapq.heappush(open_list, (new_cost, new_state)) # 将新状态加入优先队列came_from[tuple(map(tuple, new_state))] = tuple(map(tuple, current_state)) # 更新新状态的父节点信息# 无可行解return expanded_nodes, 0, None
测试
首先,定义一个函数 print_path() 用于查看路径:
def print_path(path):step = 0for state in path:print("Step. ", step)for row in state:print(row)step += 1
设置初始状态和目标状态进行测试:
# 设置初始状态和目标状态
start_state = [[2, 8, 3],[1, 6, 4],[7, 0, 5]
]goal_state = [[1, 2, 3],[8, 0, 4],[7, 6, 5]
]h1_nodes, h1_times, h1_path = astar(start_state, goal_state, h1) # 通过 h1 启发函数调用 astar 算法
h2_nodes, h2_times, h2_path = astar(start_state, goal_state, h2) # 通过 h2 启发函数调用 astar 算法if h1_path:print("调用 h1 启发函数的 A* 算法共扩展 {} 个节点,耗时 {}s,路径如下:".format(h1_nodes, h1_times))# print_path(h1_path)
else:print("调用 h1 启发函数的 A* 算法无法得到可行解。")# print("=" * 50)
if h2_path:print("调用 h2 启发函数的 A* 算法共扩展 {} 个节点,耗时 {}s,路径如下:".format(h2_nodes, h2_times))# print_path(h2_path)
else:print("调用 h2 启发函数的 A* 算法无法得到可行解。")
输出结果:(path 输出过长,这里省略)
调用 h1 启发函数的 A* 算法共扩展 28 个节点,耗时 0.00037217140197753906s,路径如下:
调用 h2 启发函数的 A* 算法共扩展 17 个节点,耗时 0.0002200603485107422s,路径如下:
测试鲁棒性——当可行解不存在时:
# 设置初始状态和目标状态
start_state = [[7, 8, 3],[1, 5, 2],[6, 0, 4]
]goal_state = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]h1_nodes, h1_times, h1_path = astar(start_state, goal_state, h1) # 通过 h1 启发函数调用 astar 算法
h2_nodes, h2_times, h2_path = astar(start_state, goal_state, h2) # 通过 h2 启发函数调用 astar 算法if h1_path:print("调用 h1 启发函数的 A* 算法共扩展 {} 个节点,耗时 {}s,路径如下:".format(h1_nodes, h1_times))# print_path(h1_path)
else:print("调用 h1 启发函数的 A* 算法无法得到可行解。")# print("=" * 50)
if h2_path:print("调用 h2 启发函数的 A* 算法共扩展 {} 个节点,耗时 {}s,路径如下:".format(h2_nodes, h2_times))# print_path(h2_path)
else:print("调用 h2 启发函数的 A* 算法无法得到可行解。")
输出结果:(path 输出过长,这里省略)
调用 h1 启发函数的 A* 算法无法得到可行解。
调用 h2 启发函数的 A* 算法无法得到可行解。
国科大的朋友们提交之前改一改哈!因为作者也是这么交的~
相关文章:

用A*算法求解八数码问题
用A*算法求解八数码问题 实现两种启发函数实现A*算法测试 实现两种启发函数 采取两种策略实现启发函数: 策略1:不在目标位置的数字个数策略2:曼哈顿距离(将数字直接移动到对应位置的步数总数) # 策略1: 不在目标位置…...
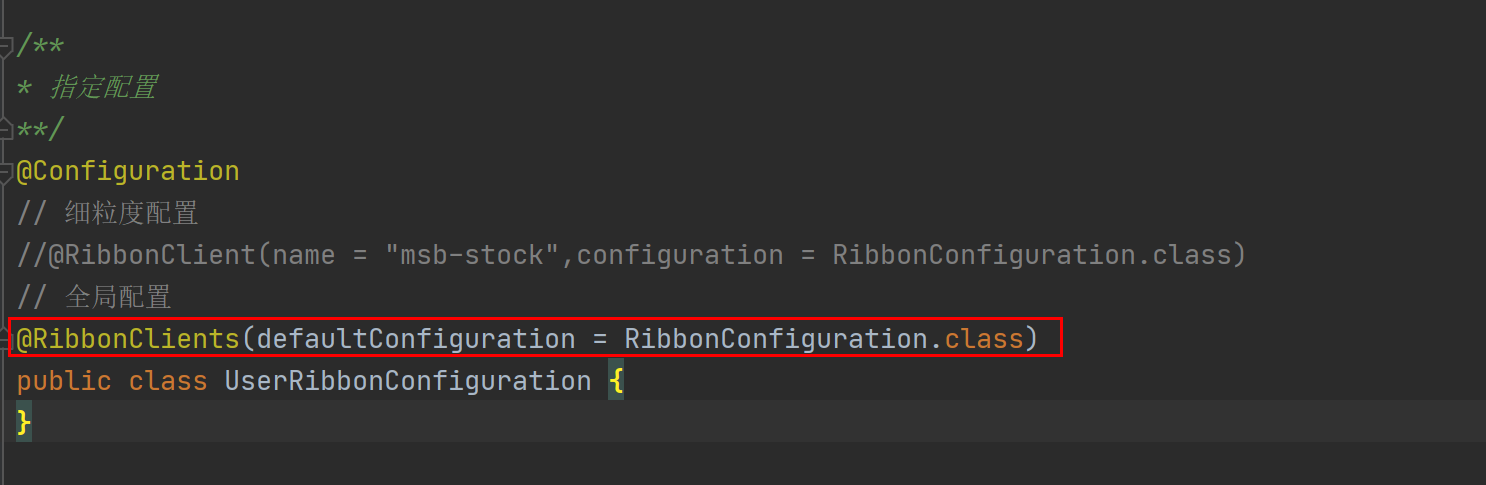
分布式之Ribbon使用以及原理
Ribbon使用以及原理 1、负载均衡的两种方式 服务器端负载均衡 传统的方式前端发送请求会到我们的的nginx上去,nginx作为反向代理,然后路由给后端的服务器,由于负载均衡算法是nginx提供的,而nginx是部署到服务器端的,所…...

android JNI float *转MutableList
data class Test(var data:MutableList<Float> )JNIEXPORT void JNICALL Java_NativeUtils_assignFloatArrayToHealth(JNIEnv *env, jclass clazz, jobject obj, jfloatArray cData) {jclass objClass env->GetObjectClass(obj);// 获取 Test类中的 data 属性jfieldI…...

chatgpt与人类有何不同?
ChatGPT和人类之间存在多个显著的差异。 首先,ChatGPT是一种基于人工智能技术的计算机程序,通过机器学习和自然语言处理等技术,从大量的数据中获取知识并生成语言输出。它主要依赖于算法和数据进行工作,能够迅速处理和检索信息&a…...
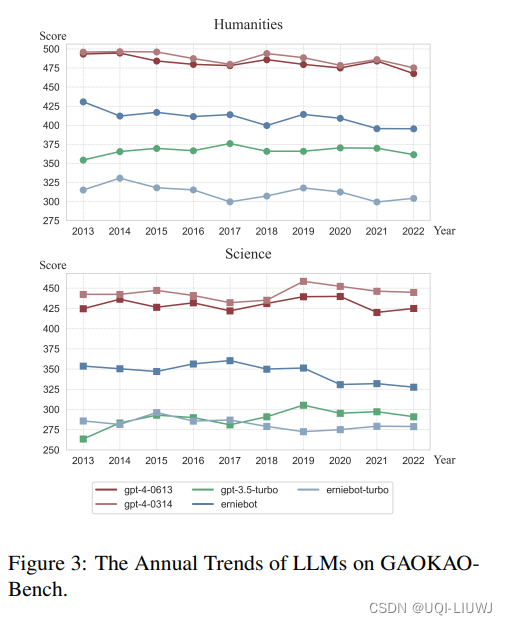
论文笔记:Evaluating the Performance of Large Language Models on GAOKAO Benchmark
1 论文思路 采用zero-shot prompting的方式,将试题转化为ChatGPT的输入 对于数学题,将公式转化为latex输入 主观题由专业教师打分 2 数据 2010~2022年,一共13年间的全国A卷和全国B卷 3 结论 3.1 不同模型的zeroshot 高考总分 3.2 各科主…...

MySQL 数据库查询与数据操作:使用 ORDER BY 排序和 DELETE 删除记录
使用 ORDER BY 进行排序 使用 ORDER BY 语句按升序或降序对结果进行排序。 ORDER BY 关键字默认按升序排序。要按降序排序结果,使用 DESC 关键字。 示例按名称按字母顺序排序结果: import mysql.connectormydb mysql.connector.connect(host"l…...

数据结构入门(3)2.链表接口实现
目录 前言 头文件 动态申请一个结点 单链表打印 单链表尾插 单链表的头插 单链表的尾删 单链表头删 单链表查找 单链表在pos位置之后插入x 单链表删除pos位置之后的值 在pos的前面插入 删除pos位置 销毁顺序表 前言 本文将介绍链表常见的功能的实现 头文件 #…...
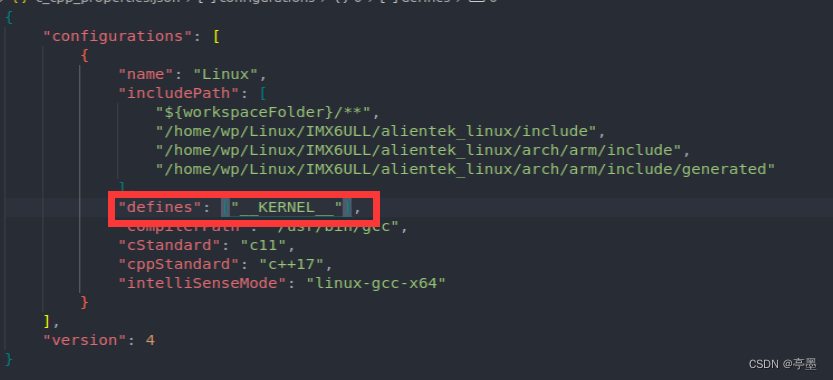
vscode中解决驱动编写的时候static int __init chrdev_init()报错的问题
目录 错误出错原因解决方法 错误 在入口函数上,出现 expected a ; 这样的提示 出错原因 缺少了 __KERNEL __ 宏定义 解决方法 补上__KERNEL__宏定义 具体做法:在vscode中按下ctrlshiftp ,输入:C/C:Edit Configurations࿰…...

fastgpt本地详细部署以及配置
目录 一、Docker部署1、docker安装2、docker启动3、添加用户到 docker 组:4、验证 Docker 安装:二、one_api 本地部署1、linux系统部署2、windows系统部署三、向量模型部署(m3e)四、chatglm2模型本地部署五、fastgpt模型本地部署1、下载配置文件2、文件配置--docker-compos…...

【故障分类】基于注意力机制的卷积神经网络结合双向长短记忆神经网络CNN-BiLSTM-attention实现数据分类附matlab代码
摘要: ntion机制加权 4. 加权后的特征进行分类 需求分析 本文旨在实现一个通用的数据分类模型,可应用于不同领域的数据分类任务。 设计方案 设计一个CNN网络结构,提取输入数据的特征 将特征序列输入到BiLSTM网络,进行时序建模…...
vue接入百度地图获取经纬度
通过城市名称和城市中心经纬度来获取当前所在地图,当前经纬度中心获取可以通过后端获取 静态文件包,替换baidu.html中的ak值,ak值通过百度地图官方网站申请 申请:百度地图API申请步骤 - 知乎 代码示例文件: 链接&a…...

交流负载箱的特点和优势有哪些?
交流负载箱广泛应用于电力系统、新能源、轨道交通、航空航天等领域。它具有以下特点和优势: 1. 灵活性高:交流负载箱可以根据实际需求,调整输出电流、电压、功率等参数,以满足不同场景下的测试需求。同时,它还可以实现…...

Java线程锁之Lock的使用
Lock 的使用 Lock 是java 1.5 中引入的线程同步工具,它主要用于多线程下共享资源的控制。本质上Lock 仅仅是一个接口, 可以通过显式定义同步锁对象来实现同步,能够提供比synchronized 更广泛的锁定操作,并支持多个相关的 Lock接…...
简站wordpress主题看上去差不多 实际大不一样
有人说简站wordpress主题,都差不多嘛。我表示无语。表面看上去是差不多的,实际的细节是不一样的。 下面以编号:JZP4431和编号:JZP4878这两个主题为例子来讲一下,简站wordpress主题,在细节方面的不一样之处…...
(完美方案)解决mfc140u.dll文件丢失问题,快速且有效的修复
唉,又是丢失了mfc140u.dll,这该怎么办呢?如果你的电脑突然找不到或丢失mfc140u.dll文件,那就真是太糟糕了。别担心,我分享给你一些干货,告诉你如何快速解决mfc140u.dll丢失的问题。 一.mfc140u.dll属性功能…...

并发通信(网络进程线程)
如果为每个客户端创建一个进程(或线程),因为linux系统文件标识符最多1024位,是有限的。 所以使用IO复用技术,提高并发程度。 阻塞与非阻塞 阻塞式复用 非阻塞复用 信号驱动IO 在属主进程(线程中声明&…...

WPF 该线程是用不接受参数的 ThreadStart 委托创建的。
创建无参数线程是无法发去传递参数的,需要把 《 thread.Start(“张三”); 》改为《 thread.Start(); 》 把参数去掉就可以了。 public RegisterWindow(){InitializeComponent();//无参数线程Thread thread new Thread(pageLoad);thread.IsBackground true;//thr…...

FreeRTOS学习第9篇--队列介绍
目录 FreeRTOS学习第9篇--队列介绍1. 数据传输的方法1.1 任务之间如何传输数据1.2 队列的本质 2. 队列的工作原理和实现2.1 创建队列2.2 向队列发送数据2.3 从队列接收数据 3. 使用队列进行任务间的通信3.1 通信示例3.2 同步示例 结论 FreeRTOS学习第9篇–队列介绍 本文目标&a…...

qt如何配置ros环境
在Qt5.7的版本可以使用bash -i -c来启动qt,让Qt自己识别系统环境,不知道为什么Qt在之后的版本,这样使用都失效了。因为它会默认把CMAKE_PREFIX_PATH修改掉。 网上还有安装ros插件版本的qt creator,感觉失去了一些灵活性。 自己测试…...

20240310-1-Java后端开发知识体系
Java 基础 知识体系 Questions 1. HashMap 1.8与1.7的区别 1.71.8底层结构数组链表数组链表/红黑树插入方式头插法尾插法计算hash值4次位运算5次异或运算1次位运算1次异或运算扩容、插入先扩容再插入先插入再扩容扩容后位置计算重新hash原位置或原位置旧容量 (1) 扩容因子…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
