删除、创建、验证Kafka安装自带的__consumer_offsets topic
删除Kafka自带Topic
一般情况下,你删除Kafka自带的__consumer_offsets topic,会报错提示不能删除。
倔强的你直接找到zookeeper删掉了它,list查看确实没有这个topic了,但是这会导致消费者和偏移量无法记录。
创建Kafka自带的Topic
如果尝试直接创建,不带参数,那么创建完成后,leader会显示none,ISR显示为空。
正确的创建方式是:
kafka-topics --create --zookeeper xxxx:2181 --replication-factor 3 --partitions 50 --topic __consumer_offsets --config cleanup.policy=compact --config min.compaction.lag.ms=86400000
保留期限可以自己调整,其他的参数不能变,否则不能被Kafka管理。
验证方式
- describe查看__consumer_offsets ,是否有leader、ISR
- 随便找一个topic(如topic_test,然后新建一个消费者
- 查看topic_test的消费者组,如果能查询出来,即为成功。
相关文章:

删除、创建、验证Kafka安装自带的__consumer_offsets topic
删除Kafka自带Topic 一般情况下,你删除Kafka自带的__consumer_offsets topic,会报错提示不能删除。 倔强的你直接找到zookeeper删掉了它,list查看确实没有这个topic了,但是这会导致消费者和偏移量无法记录。 创建Kafka自带的Topi…...

在文件夹下快速创建vue项目搭建vue框架详细步骤
一、首先在你的电脑目录下新建一个文件夹 进入该文件夹并打开控制台(输入cmd指令) 进入控制台后输入 vue create springboot_vue (自己指定名称) 如果出现这类报错如:npm install 的报错npm ERR! network request to http://registry.cnp…...

蓝桥杯倒计时 36天-DFS练习
文章目录 飞机降落仙境诅咒小怂爱水洼串变换 飞机降落 思路:贪心暴搜。 #include<bits/stdc.h>using namespace std; const int N 10; int t,n; //这题 N 比较小,可以用暴力搜搜复杂度是 TN*N! struct plane{int t,d,l; }p[N]; bool vis[N];//用…...
ctfshow web入门 php特性总结
1.web89 intval函数的利用,intval函数获取变量的整数值,失败时返回0,空的数组返回,非空数组返回1 num[]1 intval ( mixed $var [, int $base 10 ] ) : int Note: 如果 base 是 0,通过检测 var 的格式来决定使用的进…...

Media Encoder 2024:未来媒体编码的新纪元 mac/win版
随着科技的飞速发展,媒体内容已成为我们日常生活中不可或缺的一部分。为了满足用户对高质量视频内容不断增长的需求,Media Encoder 2024应运而生,它凭借卓越的技术和创新的特性,重塑了媒体编码的未来。 Media Encoder 2024 mac/w…...

2024年AI辅助研发趋势:数智时代革新新引擎
随着科技的飞速发展,人工智能(AI)已经渗透到我们生活的方方面面,而在软件开发领域,AI辅助研发正成为一股不可忽视的力量。本文将探讨2024年AI辅助研发的趋势,以及它如何成为数智时代革新的新引擎。 AI辅助研…...

2024年家政预约上门服务小程序【用户端+商家端+师傅端】源码
024最新家政预约上门服务小程序源码 主要功能:商家入住,师傅入住,缴纳保正金 支持师傅,抢单派单 支持多城市多门下单,支持预约上门服务到店核销 支持补差价义价,支持区域服务限制 基于thinkphp和原生小程序开发...

数据结构:静态链表(编程技巧)
链表的元素用数组存储, 用数组的下标模拟指针。 一、理解 如果有些程序设计语言没有指针类型,如何实现链表? 在使用指针类型实现链表时,我们很容易就可以直接在内存中新建一块地址用于创建下一个结点,在逻辑上&#x…...

python中的**可以表示什么??
在Python中,** 有两个主要的用途: 作为幂运算符:a ** b 表示a的b次方。例如,2 ** 3 会返回 8,因为2的3次方等于8。 在函数调用或定义时作为关键字参数的解包: 当你有一个字典,并且你想将这个字…...

使用 Git 跟踪项目文件
本章内容为:用Django 写学习笔记程序第三章.2部署程序摘录,详情内容查看请跳转下方链接: 用Django 写学习笔记程序第三章.2部署程序 文章目录 使用 Git 跟踪项目文件虚拟环境中安装 gitgit 是什么git 安装完成后的简单配置创建项目忽略文件初…...
——set,map学习使用)
C++从零开始(day47)——set,map学习使用
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于set和map的知识点 1.关联式容器 在前面&#…...
手机和电脑同步的好用记事本软件有哪些
我常常需要随手记录各种信息,以便随时查阅和使用。比如,在下班路上,我会用手机记录明天要处理的工作事项、购物清单,或是某个突然迸发的创意想法;而在办公室,我则需要在电脑上整理会议纪要、项目计划&#…...

使用CSS制作动态的环形图/饼图
使用纯 CSS Animation conic-gradient 实现一个环形图。 饼图的实现思路和环形图一样,去掉中间的圆形遮盖 after 伪类元素即可。 一、构建基础样式 构建圆形节点和中间的遮盖元素。 <style>body {background-color: rgb(130, 226, 255);}.circle {top: 16…...

掌握React中的useEffect:函数组件中的魔法钩子
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
WPF 窗口添加投影效果Effect
BlurRadius:阴影半径 Color:颜色 Direction:投影方向 ShadowDepth:投影的深度 <Window.Effect><DropShadowEffect BlurRadius"10" Color"#FF858484" Direction"300" ShadowDepth&quo…...
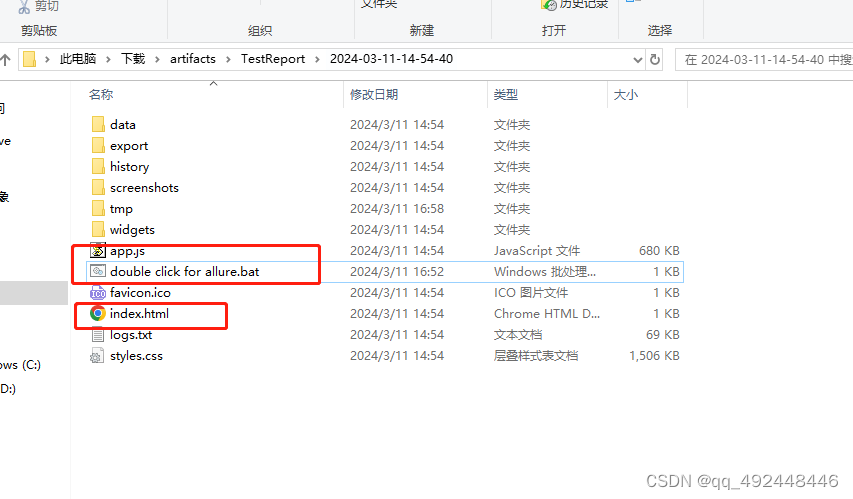
Gitlab CICD 下载artifacts文件并用allure打开,或bat文件打开
allure命令行打开aritfacts报告 首先下载allure.zip,并解压 配置环境变量 使用命令行打开allure文件夹 allure open 2024-03-11-14-54-40 2024-03-11-14-54-40 包含index.html Bat文件打开artifacts There are 2 html reports in the download artifacts.zip S…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:NavRouter)
导航组件,默认提供点击响应处理,不需要开发者自定义点击事件逻辑。 说明: 该组件从API Version 9开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 必须包含两个子组件,其中第二个子组…...

Django环境下使用Ajax
Django环境下使用Ajax 目录 Django环境下使用Ajax介绍前情提要示例JS实现Ajax实现 传递JSON格式数据传递文件数据Django自带的序列化组件基于jsonresponse序列化数据基于Django自带的serializers 注册示例 介绍 AJAX 的主要目标是在不刷新整个页面的情况下,通过后台…...
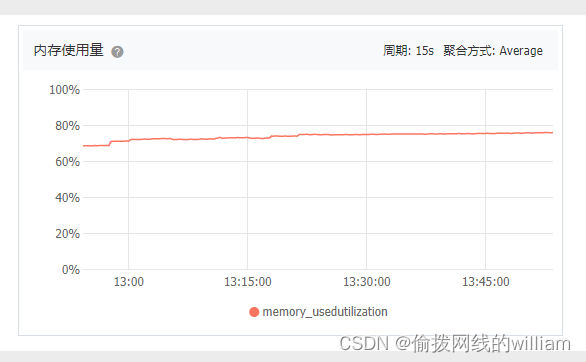
官方安装配置要求服务器最低2核4G
官方安装配置要求服务器至少2核、4G。 如果服务器低于这个要求,就没有必要安装,因为用户体验超级差。 对于服务器CPU来说,建议2到4核就完全足够了,太多就浪费了,但是内存越大越好,最好是4G以上。 如果服务器…...
Apache的运用与实战
WEB服务器 1、WEB服务简介 # 目前最主流的三个Web服务器是Apache、Nginx、 IIS。 - WEB服务器一般指网站服务器,可以向浏览器等Web客户端提供网站的访问,让全世界浏览。 - WEB服务器也称为WWW(WORLD WIDE WEB)服务器,主要功能是提供网上信息…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
