使用hashmap优化时间复杂度,leetcode1577
1577. 数的平方等于两数乘积的方法数
已解答
中等
相关标签
相关企业
提示
给你两个整数数组 nums1 和 nums2 ,请你返回根据以下规则形成的三元组的数目(类型 1 和类型 2 ):
- 类型 1:三元组
(i, j, k),如果nums1[i]2 == nums2[j] * nums2[k]其中0 <= i < nums1.length且0 <= j < k < nums2.length - 类型 2:三元组
(i, j, k),如果nums2[i]2 == nums1[j] * nums1[k]其中0 <= i < nums2.length且0 <= j < k < nums1.length
示例 1:
输入:nums1 = [7,4], nums2 = [5,2,8,9] 输出:1 解释:类型 1:(1,1,2), nums1[1]^2 = nums2[1] * nums2[2] (4^2 = 2 * 8)
示例 2:
输入:nums1 = [1,1], nums2 = [1,1,1] 输出:9 解释:所有三元组都符合题目要求,因为 1^2 = 1 * 1 类型 1:(0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2), nums1[i]^2 = nums2[j] * nums2[k] 类型 2:(0,0,1), (1,0,1), (2,0,1), nums2[i]^2 = nums1[j] * nums1[k]
示例 3:
输入:nums1 = [7,7,8,3], nums2 = [1,2,9,7] 输出:2 解释:有两个符合题目要求的三元组 类型 1:(3,0,2), nums1[3]^2 = nums2[0] * nums2[2] 类型 2:(3,0,1), nums2[3]^2 = nums1[0] * nums1[1]
示例 4:
输入:nums1 = [4,7,9,11,23], nums2 = [3,5,1024,12,18] 输出:0 解释:不存在符合题目要求的三元组
提示:
1 <= nums1.length, nums2.length <= 10001 <= nums1[i], nums2[i] <= 10^5
解决思路:直观来看,直接暴力遍历算法也是正确的,然而时间复杂度比较高O(n^3),根据leetcode的规律,只有数据规模小于100的时候,才能使用这个复杂度的算法。所以,需要优化,这里使用哈希表记录每个数组的平方值,然后统计第二个数组中nums1[j] * nums1[k] 是否==第一个数组中的平方值,有的话就相加,没有就继续。复杂度可以降低为O(n^2),通过测试。
class Solution {
public:int numTriplets(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();unordered_map<long, int> square_count1;unordered_map<long, int> square_count2;int count = 0;// 计算 nums1 和 nums2 每个元素的平方,并存储在哈希表中for (int num : nums1) {long square = (long)num * num;square_count1[square]++;}for (int num : nums2) {long square = (long)num * num;square_count2[square]++;}// 枚举 nums1 的所有可能的两个元素的乘积for (int i = 0; i < n; ++i) {for (int j = i + 1; j < n; ++j) {long product = (long)nums1[i] * nums1[j];// 检查 product 的平方是否在哈希表中count+=square_count2[product];}}// 枚举 nums2 的所有可能的两个元素的乘积for (int i = 0; i < m; ++i) {for (int j = i + 1; j < m; ++j) {long product = (long)nums2[i] * nums2[j];// // 检查 product 的平方是否在哈希表中count+=square_count1[product];}}return count;}
};执行用时分布
135ms
击败34.58%使用 C++ 的用户
消耗内存分布
37.60MB
击败9.34%使用 C++ 的用户
官方题解给了更快的算法。随着AI的大模型普及,以后程序员可能会成为历史,可能以后编程就是提示和应用工程师。但是算法的思想和解决问题的能力,这个暂时是AI无法替代的。
相关文章:

使用hashmap优化时间复杂度,leetcode1577
1577. 数的平方等于两数乘积的方法数 已解答 中等 相关标签 相关企业 提示 给你两个整数数组 nums1 和 nums2 ,请你返回根据以下规则形成的三元组的数目(类型 1 和类型 2 ): 类型 1:三元组 (i, j, k) ÿ…...

3、设计模式之工厂模式1
工厂模式是什么? 工厂模式是一种创建者模式,用于封装和管理对象的创建,屏蔽了大量的创建细节,根据抽象程度不同,主要分为简单工厂模式、工厂方法模式以及抽象工厂模式。 简单工厂模式 看一个具体的需求 看一个…...
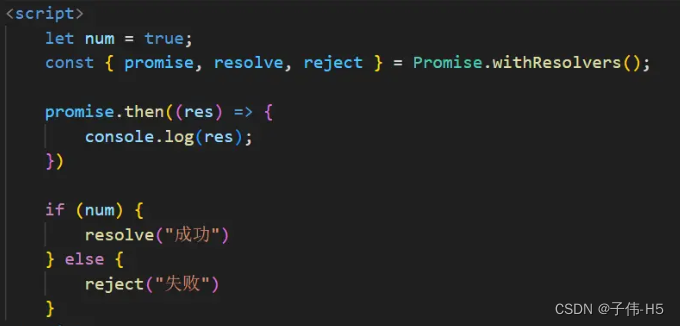
一个Promise全新API
1. 资讯速览 最近,Promise 新出了一个方法,已经进入 Stage 3 (候选阶段) ,相信很快就能达到 Stage 4 (完成阶段),并在项目中广泛使用。 这个方法就是 Promise.withResolvers。它是…...
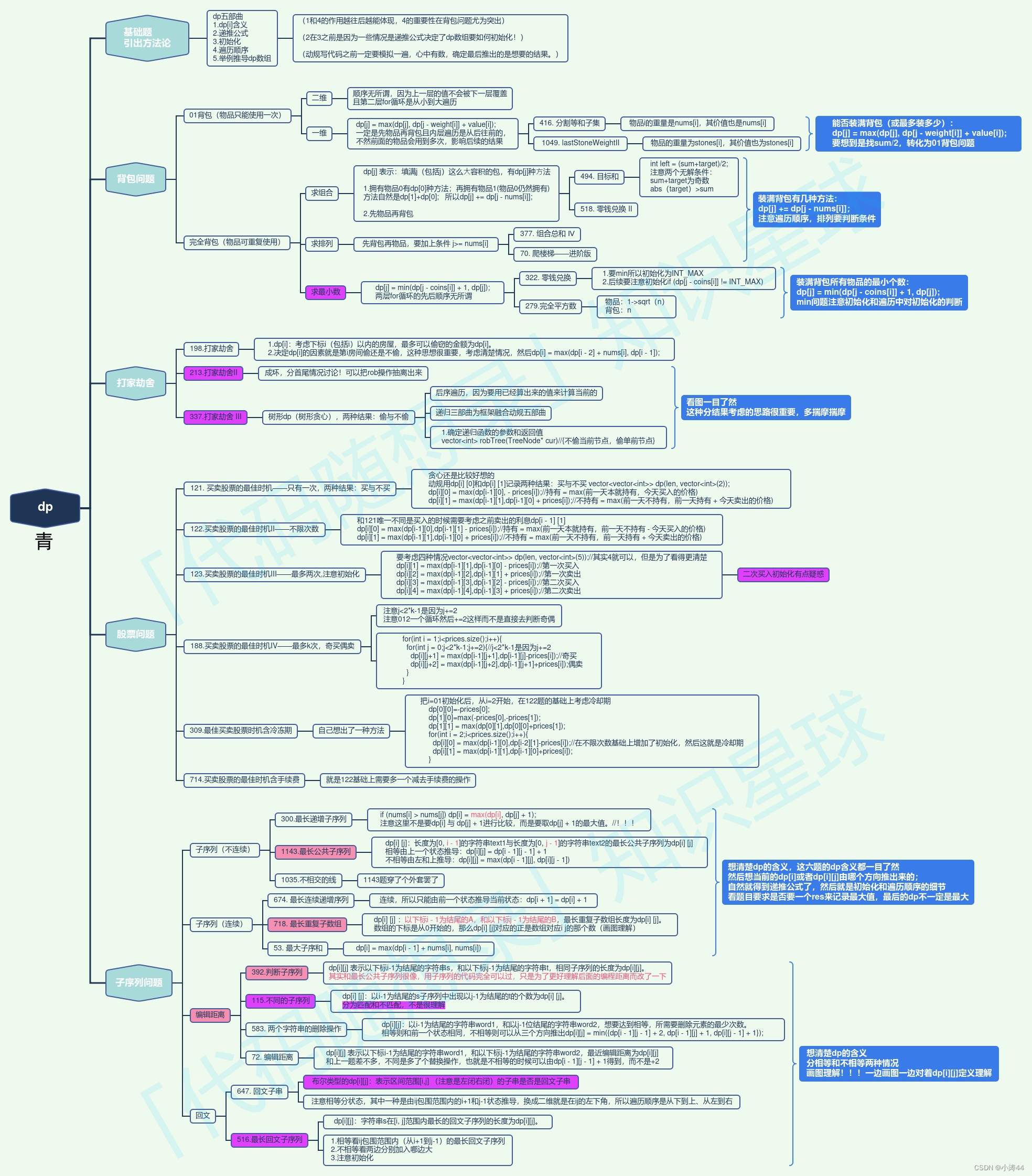
【力扣hot100】刷题笔记Day25
前言 这几天搞工作处理数据真是类似我也,还被老板打电话push压力有点大的,还好搞的差不多了,明天再汇报,赶紧偷闲再刷几道题(可恶,被打破连更记录了)这几天刷的是动态规划,由于很成…...

webpack5零基础入门-4使用webpack处理less文件
1.安装less npm install less -D 2.创建less文件 .box{width: 100px;height: 100px;background: red; } 3.引入less文件并打包 执行npx webpack 报错无法识别less文件 4.安装less-loader并配置 npm install less-loader9 -D 这里指定一下版本不然会因为node版本过低报错 …...

Python机器学习预测+回归全家桶,新增TCN,BiTCN,TCN-GRU,BiTCN-BiGRU等组合模型预测...
截止到本期,一共发了4篇关于机器学习预测全家桶Python代码的文章。参考往期文章如下: 1.机器学习预测全家桶-Python,一次性搞定多/单特征输入,多/单步预测!最强模板! 2.机器学习预测全家桶-Pythonÿ…...
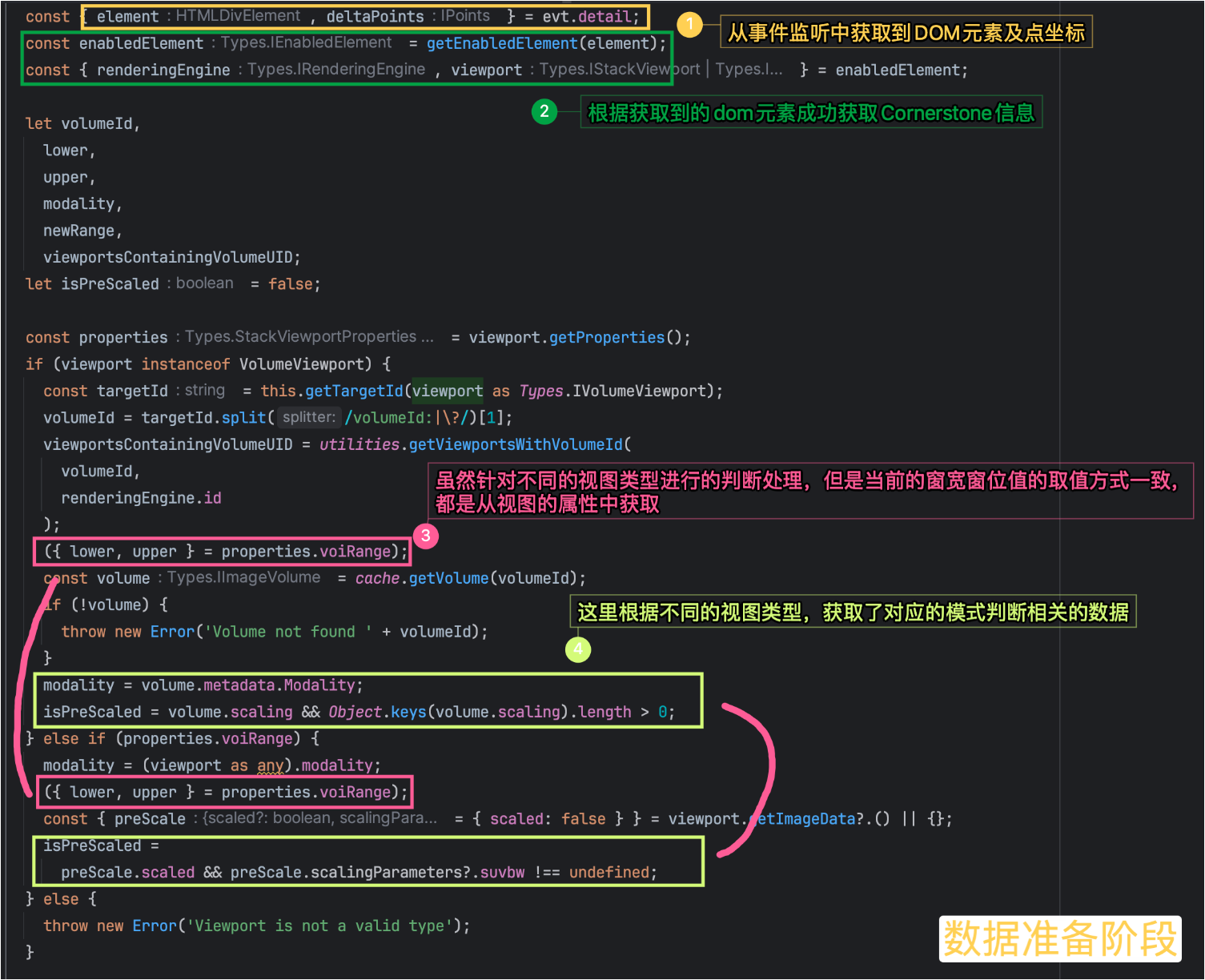
一文了解Cornerstone3D中窗宽窗位的3种设置场景及原理
🔆 引言 在使用Cornerstone3D渲染影像时,有一个常用功能“设置窗宽窗位(windowWidth&windowLevel)”,通过精确调整窗宽窗位,医生能够更清晰地区分各种组织,如区别软组织、骨骼、脑组织等。…...

部署 LVS(nginx)+keepalived高可用负载均衡集群
目录 一、集群的概述 1、什么是集群 2、普通集群与负载均衡集群 2.1 普通集群(Regular Cluster) 2.2 负载均衡集群(Load Balancing Cluster) 2.3 高可用集群(High Availability Cluster) 2.4 区别 …...
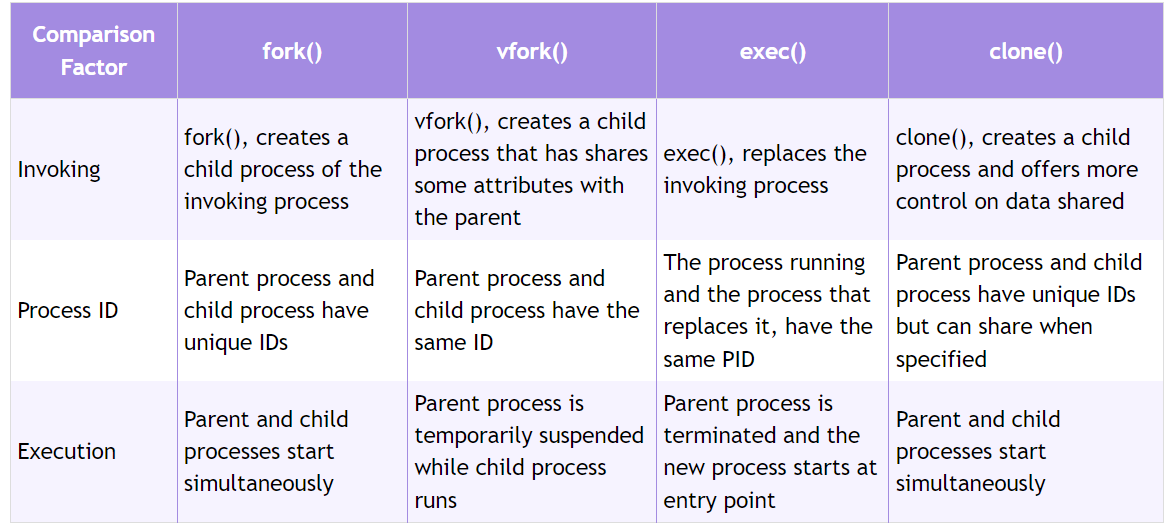
Qt/QML编程之路:fork、vfork、exec、clone的对比及使用(46)
前言: 系统调用system call是OS提供的服务提供接口。系统调用fork()、vfork()、exec()和clone()都用于创建和操作进程。Linux下Qt编程也会用到vfork进行多进程间通信。让我们看一下以下每个系统调用的概述和比较: fork()、vfork()和clone()的工作原理相似,但在处…...
Go语言框架路由Controller控制器设计思路gin路由根据控制器目录分层生成路由地址
Controller设计好处 框架设计用controller分请求路由层级,应用从app目录开始对应请求url路由地址,这样设计师方便开发时候通过请求地址层级快速定位接口方法对应的代码位置。 例如api接口请求路径为:http://localhost:8110/busines…...
)
突破编程_C++_设计模式(责任链模式)
1 责任链模式的概念 责任链模式(Chain of Responsibility Pattern)是一种行为设计模式,它允许对象以链式的方式组织起来,以便对请求进行处理。这种模式为多个对象处理同一请求提供了一个灵活的机制,而无需在发送者和多…...

php开发100问?
什么是 PHP?PHP 是一种什么类型的语言?PHP 的优缺点是什么?如何在服务器上配置 PHP?PHP 中的变量是如何声明和使用的?如何在 PHP 中输出文本和变量?什么是 PHP 的数据类型?如何在 PHP 中实现条件…...
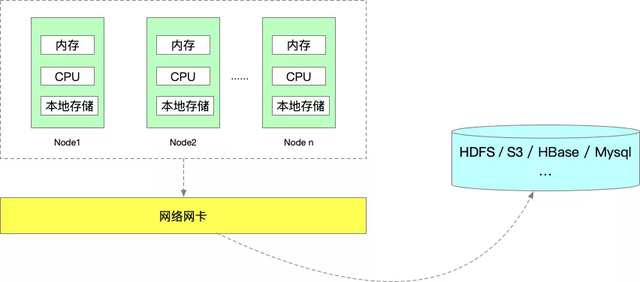
flink实战--Flink任务资源自动化优化
背景 在生产环境Flink任务资源是用户在实时平台端进行配置,用户本身对于实时任务具体配置多少资源经验较少,所以存在用户资源配置较多,但实际使用不到的情形。比如一个 Flink 任务实际上 4 个并发能够满足业务处理需求,结果用户配置了 16 个并发,这种情况会导致实时计算资…...

tsv文件在大数据技术栈里的应用场景
是的,\t 是指制表符(tab),它通常用作字段分隔符在 TSV(Tab-Separated Values)格式的文件中。TSV是一种简单的文本格式,它使用制表符来分隔每一列中的值,而每一行则代表一个数据记录。…...
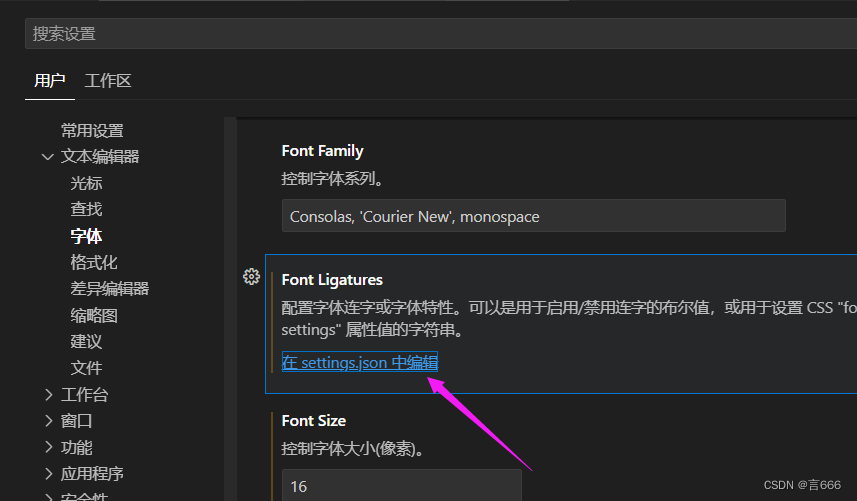
vscode设置setting.json
{ // vscode默认启用了根据文件类型自动设置tabsize的选项 "editor.detectIndentation": false, // 重新设定tabsize "editor.tabSize": 2, // #每次保存的时候自动格式化 // "editor.formatOnSave": true, // #每次保存的时候将代码按eslint格式…...

Docker的安装及镜像加速的配置
文章目录 一.切换到root二.卸载旧版docker三.配置docker的yum库四.安装Docker五.Docker的启动和验证六.配置Docker阿里云镜像加速(全程免费) 该文章文章演示在Linux系统中安装docker,Windows安装docker请参考以下文章 Windows系统中安装docker及镜像加速的配置 一…...
:从“商业画布”到“个人画布”)
AIGC时代IT人的迷茫有解(1):从“商业画布”到“个人画布”
IT人的迷茫和心态调整 最近打开新闻,各种IT老大都在说“AIGC时代,只要会说话,人人都会具备程序员的能力”,身边也有很多程序员朋友也已经在用GPT类的产品编程了。随着AIGC的发展,除了程序员,可能很多职业都会被替代或…...
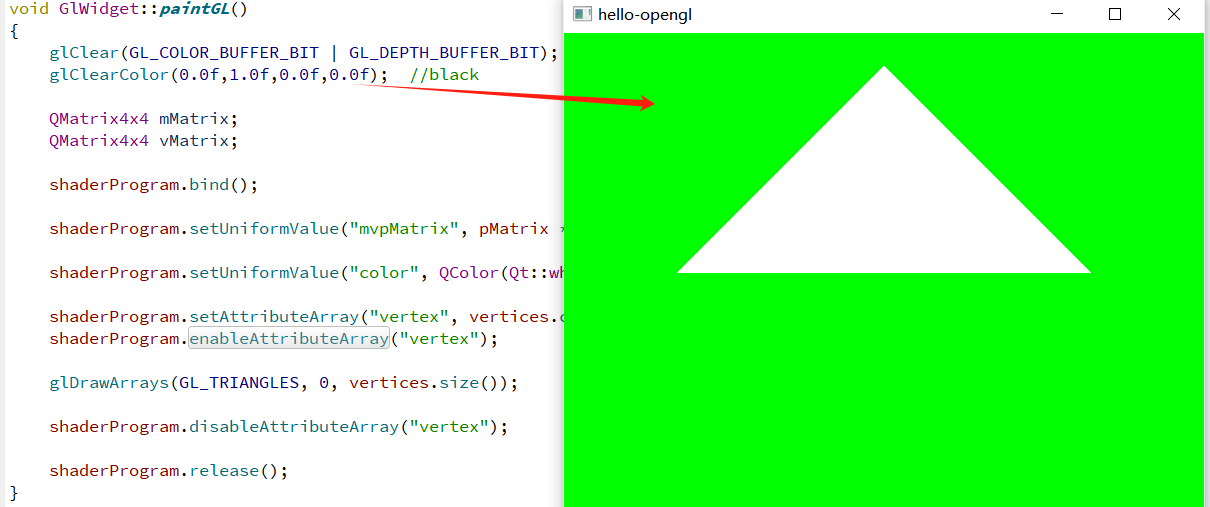
Qt/QML编程之路:openglwidget和倒车影像的切换(43)
关于如何实现一个基于OpenGL的3d 图形,这个有很多专门的介绍,我在开发中遇到了这么一个问题: 如何实现一个倒车影像的video显示与一个3D物体显示的切换,因为开窗在同样的一个位置,如果车子倒车启动,则需要将原本显示3D的地方切换为视频图像的显示。 class testOpenGl : …...

Spring 初学者遇到的问题
TagLibraryValidator Spring 实战 5.2 中有个表单需要在 jsp 中遍历数组,添加:<% taglib uri"http://java.sun.com/jsp/jstl/core" prefix"c" %>,访问时发现有些问题: java.lang.NoClassDefFoundError…...

前端解决跨域问题( 6种方法 )
本专栏是汇集了一些HTML常常被遗忘的知识,这里算是温故而知新,往往这些零碎的知识点,在你开发中能起到炸惊效果。我们每个人都没有过目不忘,过久不忘的本事,就让这一点点知识慢慢渗透你的脑海。 本专栏的风格是力求简洁…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
