人工智能|机器学习——K-means系列聚类算法k-means/ k-modes/ k-prototypes/ ......(划分聚类)
1.k-means聚类
1.1.算法简介
K-Means算法又称K均值算法,属于聚类(clustering)算法的一种,是应用最广泛的聚类算法之一。所谓聚类,即根据相似性原则,将具有较高相似度的数据对象划分至同一类簇,将具有较高相异度的数据对象划分至不同类簇。聚类与分类最大的区别在于,聚类过程为无监督过程,即待处理数据对象没有任何先验知识,而分类过程为有监督过程,即存在有先验知识的训练数据集。K-Means是无监督学习的杰出代表之一。
1.1.1 牧师-村民模型
- 有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
- 听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。
- 牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点……
- 就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
1.1.2 原理
对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。给定样本集D,k-means算法针对聚类所得簇划分C最小化平方误差。这条公式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度,E值越小则簇内样本相似度越高。k-means算法通常采用欧氏距离来计算数据对象间的距离。
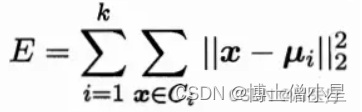
1.2 计算步骤
K-Means聚类算法步骤实质是EM算法(最大期望算法(Expectation-Maximization algorithm, EM))的模型优化过程,具体步骤如下:
- 随机选择k个样本作为初始簇类的均值向量;
- 将每个样本数据集划分离它距离最近的簇;
- 根据每个样本所属的簇,更新簇类的均值向量;
- 重复(2)(3)步,当达到设置的迭代次数或簇类的均值向量不再改变时,模型构建完成,输出聚类算法结果。
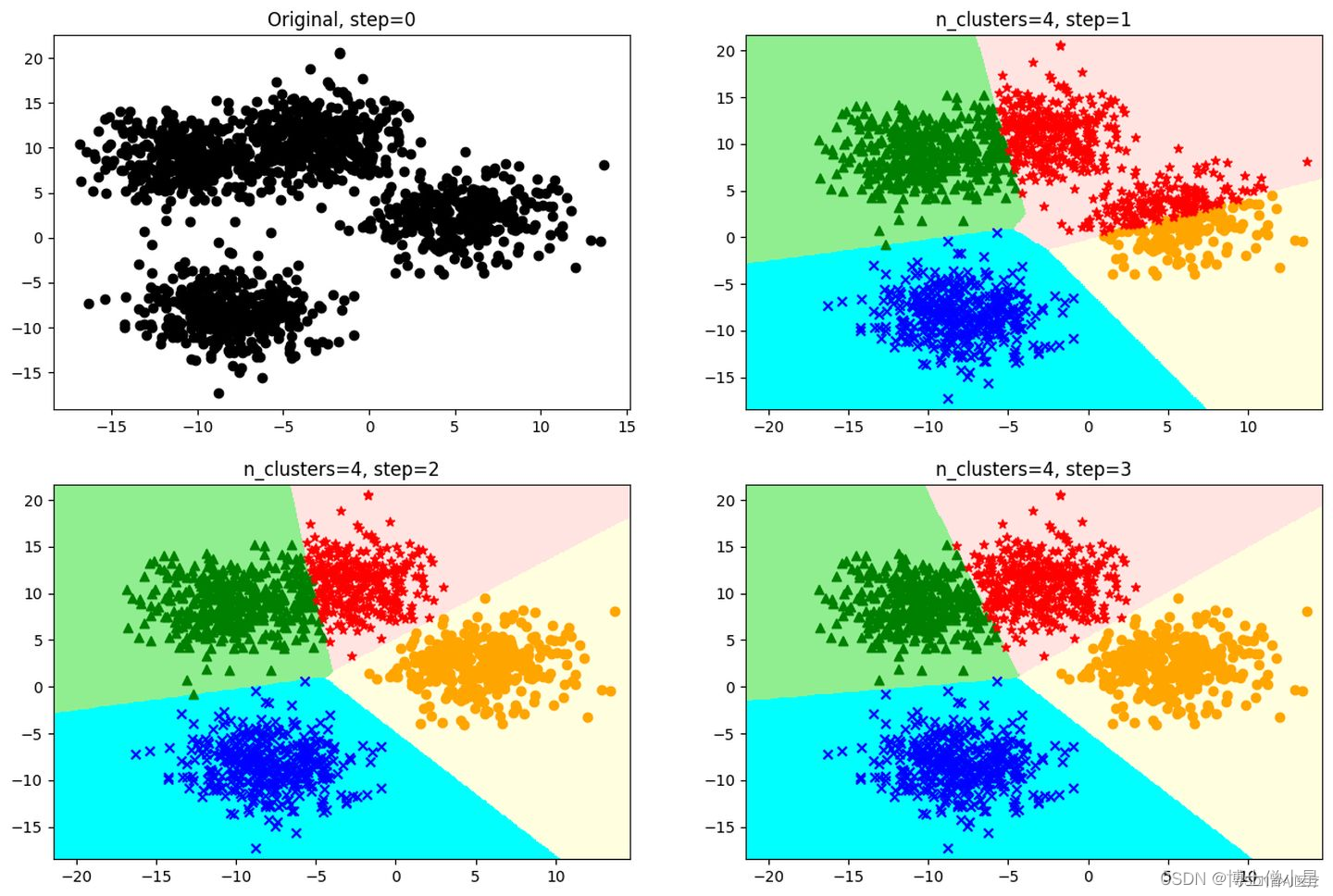
K-Means最核心的部分就是先固定中心点,调整每个样本所属的类别来减少损失值;再固定每个样本的类别,调整中心点继续减小损失值。两个过程交替循环,损失值单调递减直到最(极)小值,中心点和样本划分的类别同时收敛。
K-means 的本质是基于欧式距离的数据划分算法,均值和方差大的维度将对数据的聚类产生决定性影响。所以未做归一化处理和统一单位的数据是无法直接参与运算和比较的。常见的数据预处理方式有:数据归一化,数据标准化。
此外,离群点或者噪声数据会对均值产生较大的影响,导致中心偏移,因此我们还需要对数据进行异常点检测。
1.3 K值选择
K 值的选取对 K-means 影响很大,这也是 K-means 最大的缺点,常见的选取 K 值的方法有:手肘法、Gap statistic 方法。
- (1)手肘法
- 核心指标:SSE(sum of the squared errors,误差平方和)
- 核心思想:随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数
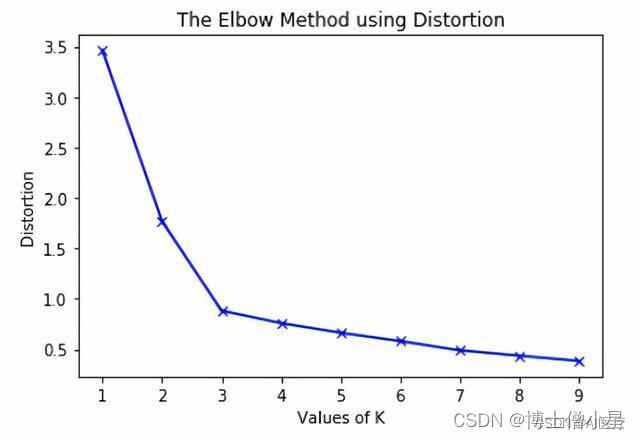
显然,肘部对于的k值为3(曲率最高),故对于这个数据集的聚类而言,最佳聚类数应该选3。
- (2)轮廓系数
手肘法的缺点在于需要人工看不够自动化,所以我们又有了 Gap statistic 方法,此方法出自斯坦福大学的论文:“estimating the number of clusters in a dataset via the gap statistic”

其中Dk为损失函数,这里E(logDk)指的是logDk的期望。这个数值通常通过蒙特卡洛模拟产生,我们在样本里所在的区域中按照均匀分布随机产生和原始样本数一样多的随机样本,并对这个随机样本做 K-Means,从而得到一个Dk。如此往复多次,通常 20 次,我们可以得到 20 个logDk。对这 20 个数值求平均值,就得到了E(logDk)的近似值。最终可以计算 Gap Statisitc。而 Gap statistic 取得最大值所对应的 K 就是最佳的 K。
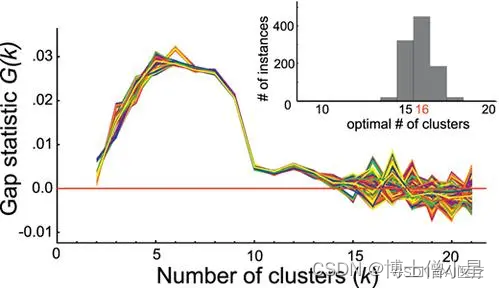
由图可见,当 K=5时,Gap(K) 取值最大,所以最佳的簇数是 K=5。
1.4 算法优缺点
- 优点:
简单而高效:K均值聚类是一种简单而直观的聚类算法,易于理解和实现。它的计算效率通常较高,特别适用于大规模数据集。
可扩展性:K均值聚类可以处理大规模数据集,并且在处理大型数据时具有较好的可扩展性。
相对较快的收敛:K均值聚类通常会在有限的迭代次数内收敛,因此在实践中运行时间较短。
对于具有明显分离簇的数据集,K均值聚类通常能够产生较好的聚类结果。
- 缺点:
对初始聚类中心的敏感性:K均值聚类对初始聚类中心的选择非常敏感。不同的初始中心可能导致不同的聚类结果,因此需要进行多次运行以选择最佳结果。
对数据分布的假设:K均值聚类假设每个簇的形状是球状的,并且簇的大小相似。对于非球状、大小差异较大或者存在重叠的簇,K均值聚类的效果可能不佳。
不适用于处理噪声和异常值:K均值聚类对噪声和异常值敏感,这些数据点可能会显著影响聚类结果。
需要预先指定簇的数量:K均值聚类需要事先确定簇的数量K。在实际应用中,选择适当的K值可能是一项挑战,且错误选择K值可能导致不合理的聚类结果。
K均值聚类是一种简单而高效的聚类算法,适用于处理大规模数据集。然而,它对初始聚类中心的选择敏感,并且对数据分布的假设要求较高。在使用K均值聚类时,需要谨慎处理噪声和异常值,并且需要合理选择簇的数量K。
1.5 应用场景
K-Means聚类算法在各个领域都有广泛的应用,主要的应用场景如下:
客户分群:K均值聚类可以用于根据客户的特征将他们分成不同的群体。这有助于企业了解其客户群体,进行个性化营销和精准定位。
市场细分:K均值聚类可以根据市场调研数据将消费者细分为不同的市场细分群体。这有助于企业理解市场需求,制定更精确的市场策略。
图像分割:K均值聚类可以应用于图像处理中的分割任务。通过将图像像素分配到不同的簇中,可以将图像分割为具有相似特征的区域,有助于对象识别、图像分析等应用。
文本聚类:K均值聚类可以用于将文本文档分成不同的主题类别。这对于文本分类、信息检索和文本挖掘等任务非常有用。
推荐系统:K均值聚类可以用于用户行为数据的聚类分析,从而为推荐系统提供个性化的推荐。通过将用户分为不同的群组,可以向每个群组提供特定的推荐内容。
K均值聚类可应用于各种需要对数据进行分组或聚类的任务。根据具体问题和数据特征,可以灵活应用K均值聚类算法。
1.6 Python实现
- 数据集
density,ratio
0.697,0.460
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.360,0.370
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459
- 代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import randomdataset = pd.read_csv('watermelon.csv', delimiter=",")
data = dataset.valuesprint(dataset)def distance(x1, x2): # 计算距离return sum((x1-x2)**2)def Kmeans(D,K,maxIter):m, n = np.shape(D)if K >= m:return DinitSet = set()curK = Kwhile(curK>0): # 随机选取k个样本randomInt = random.randint(0, m-1)if randomInt not in initSet:curK -= 1initSet.add(randomInt)U = D[list(initSet), :] # 均值向量,即质心C = np.zeros(m)curIter = maxIter # 最大的迭代次数while curIter > 0:curIter -= 1# 计算样本到各均值向量的距离for i in range(m):p = 0minDistance = distance(D[i], U[0])for j in range(1, K):if distance(D[i], U[j]) < minDistance:p = jminDistance = distance(D[i], U[j])C[i] = pnewU = np.zeros((K, n))cnt = np.zeros(K)for i in range(m):newU[int(C[i])] += D[i]cnt[int(C[i])] += 1changed = 0# 判断质心是否发生变化,如果发生变化则继续迭代,否则结束for i in range(K):newU[i] /= cnt[i]for j in range(n):if U[i, j] != newU[i, j]:changed = 1U[i, j] = newU[i, j]if changed == 0:return U, C, maxIter-curIterreturn U, C, maxIter-curIterU, C, iter = Kmeans(data,3,20)f1 = plt.figure(1)
plt.title('watermelon')
plt.xlabel('density')
plt.ylabel('ratio')
plt.scatter(data[:, 0], data[:, 1], marker='o', color='g', s=50)
plt.scatter(U[:, 0], U[:, 1], marker='o', color='r', s=100)
m, n = np.shape(data)
for i in range(m):plt.plot([data[i, 0], U[int(C[i]), 0]], [data[i, 1], U[int(C[i]), 1]], "c--", linewidth=0.3)
plt.show()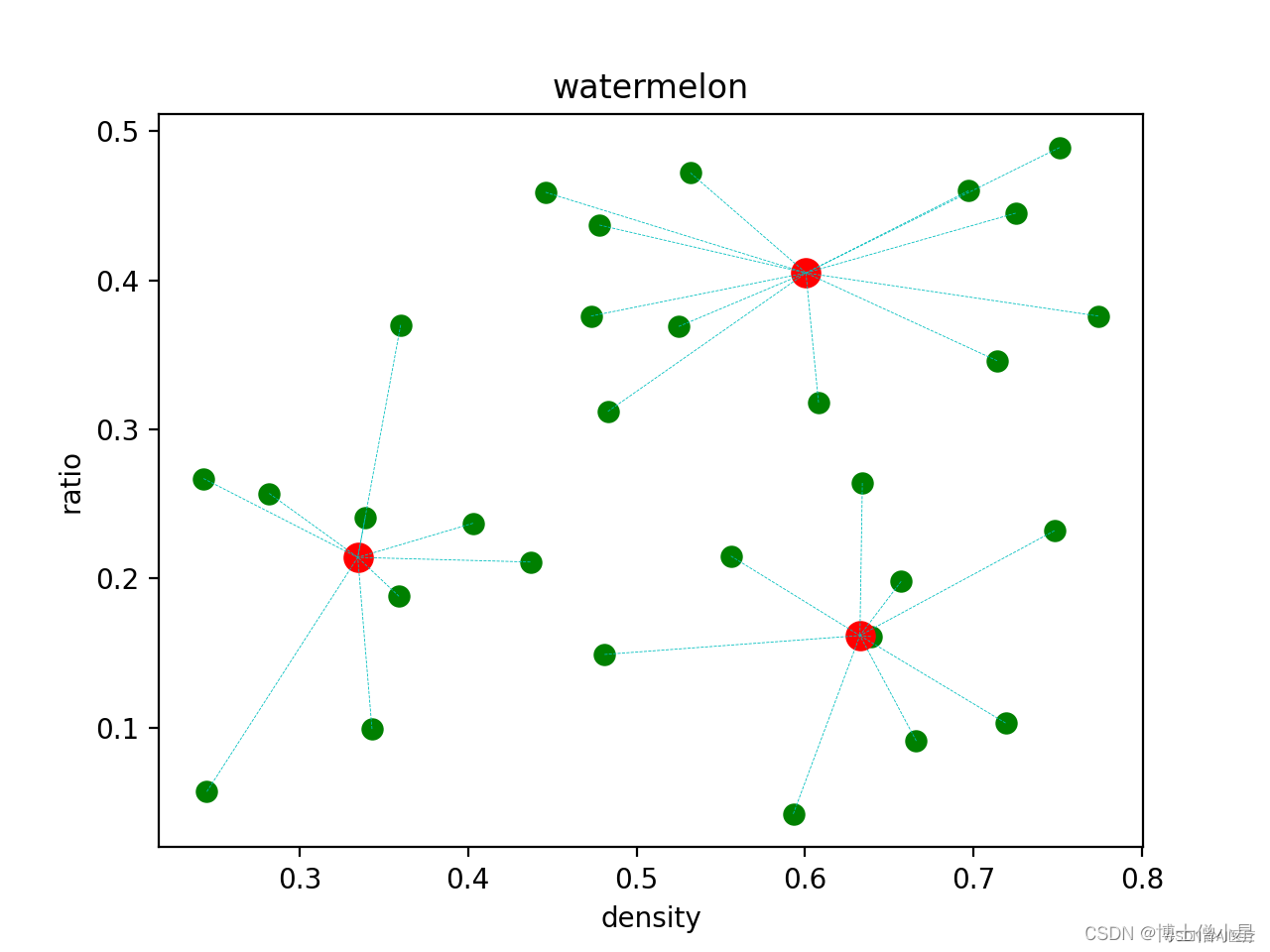
2.K-modes聚类
2.1 算法简介
k-means算法是一种简单且实用的聚类算法,但是传统的k-means算法只适用于连续属性的数据集(数值型数据),而对于离散属性的数据集,计算簇的均值以及点之间的欧式距离就变得不合适了。k-modes作为k-means的一种扩展(变种),距离使用汉明距离,适用于离散属性的数据集。
2.2 计算步骤
K-modes是数据挖掘中针对分类属性型数据进行聚类采用的方法,其算法思想比较简单,时间复杂度也比K-means、K-medoids低,大致思想如下:假设有N个样本,M个属性且全是离散的,簇的个数为k

算例:


2.3 Python实现
import numpy as np
from kmodes import kmodes'''生成互相无交集的离散属性样本集'''
data1 = np.random.randint(1,6,(10000,10))
data2 = np.random.randint(6,12,(10000,10))data = np.concatenate((data1,data2))'''进行K-modes聚类'''
km = kmodes.KModes(n_clusters=2)
clusters = km.fit_predict(data)'''计算正确归类率'''
score = np.sum(clusters[:int(len(clusters)/2)])+(len(clusters)/2-np.sum(clusters[int(len(clusters)/2):]))
score = score/len(clusters)
if score >= 0.5:print('正确率:'+ str(score))
else:print('正确率:'+ str(1-score))3.k-prototypes聚类
3.1 算法简介
K-prototypes是处理混合属性聚类的典型算法。由于K-prototypes聚类算法的时间复杂度为o(n),而聚类算法的有效性指标的时间复杂度为o(n2)。本文用python实现K-prototypes聚类算法,用pyspark来计算聚类算法的有效性指标。有效性指标其他聚类算法也可以使用。
K-prototype是K-means与K-modes的一种集合形式,适用于
数值类型与字符类型集合的混合型数据。k-prototypes算法在聚类的过程中,是将数据的数值型变量和类别型变量拆开,分开计算样本间变量的距离,再将两者相加,视为样本间的距离。k-prototypes聚类的准则就是使用一个合适的损失函数去度量数值型和分类变量对原型的距离;
3.2 算法步骤
- 随机选取k个初始原型(中心点);
- 针对数据集中的每个样本点,计算样本点与k个原型的距离(数值型变量计算欧氏距离,类别型变量计算汉明距离),将样本点划分到离它最近的中心点所对应的类别中;
- 类别划分完成后,重新确定类别的原型,数值型变量样本取值的均值作为新的原型的特征取值,类别型变量样本取值的众数作为新的原型的特征取值;
- 重复步骤2 3,直到没有样本改变类别,返回最后的聚类结果。
3.3 python内嵌API
from kmodes.kprototypes import KPrototypes-
KPrototypes(n_clusters=8)
- 参数:
- n_clusters:开始的聚类中心数量
- 整型,缺省值=8,生成的聚类数,即产生的质心(centroids)数。
- n_init :默认值:10
k-mode 算法将以不同的方式运行的次数质心种子。最终结果将是最好的输出n_init 在成本方面连续运行。 - init : {'Huang', 'Cao', 'random' 或 ndarrays 列表},默认值:'Cao'
初始化方法:
'黄':黄的方法 [1997, 1998]
'曹':曹等人的方法。 [2009]
'random':从随机选择'n_clusters'观察(行)
初始质心的数据。
如果传递了 ndarrays 列表,则它的长度应为 2,其中
数字和分类的形状(n_clusters,n_features)
数据分别。这些是初始质心。 - verbose
- n_clusters:开始的聚类中心数量
方法:
- estimator.fit(x)
- estimator.predict(x)
- estimator.fit_predict(x)
- 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)
- 参数:
3.4 K值选择方法
同上
3.5 Python实现
3.5.1 内嵌函数实现
#!/usr/bin/env pythonimport timeitimport numpy as npfrom kmodes.kprototypes import KPrototypes# number of clusters
K = 20
# no. of points
N = int(1e5)
# no. of dimensions
M = 10
# no. of numerical dimensions
MN = 5
# no. of times test is repeated
T = 3data = np.random.randint(1, 1000, (N, M))def huang():KPrototypes(n_clusters=K, init='Huang', n_init=1, verbose=2)\.fit_predict(data, categorical=list(range(M - MN, M)))def cao():KPrototypes(n_clusters=K, init='Cao', verbose=2)\.fit_predict(data, categorical=list(range(M - MN, M)))if __name__ == '__main__':for cm in ('huang', 'cao'):print(cm.capitalize() + ': {:.2} seconds'.format(timeit.timeit(cm + '()',setup='from __main__ import ' + cm,number=T)))
3.5.2 面向过程的实现
import numpy as np
import pandas as pddef get_distances(cores, data: np.ndarray, Numerical, Type, gamma) -> np.ndarray:'''距离计算函数'''m, n = data.shapek = cores.shape[0]d1 = (np.abs(np.repeat(data[:, Numerical], k, axis=0).reshape(m, k, len(Numerical)) - cores[:, Numerical]))*np.array(gamma)[Numerical]distance_1 = np.sum(d1, axis=2) # ndarray(m, k)distance_2 = np.sum((np.repeat(data[:, Type], k, axis=0).reshape(m, k, len(Type)) != cores[:, Type])*np.array(gamma)[Type], axis=2)return distance_1 + distance_2def get_new_cores(result, data, cores):'''重新找聚类中心'''k = cores.shape[0]for i in range(k): # 遍历质心集items = data[result == i] # 找出对应当前质心的子样本集cores[i, Numerical] = np.mean(items[:, Numerical], axis=0) # 更新数据型数据核心for num in Type:cores[i, num] = np.argmax(np.bincount(items[:, num])) # 更新分类型数据核心return coresdef k_prototypes(data, k, Numerical, Type, gamma):"""k-means聚类算法k - int,指定分簇数量data - ndarray(m, n),m个样本的数据集,每个样本n个属性值Numerical - list,数值型数据所在列Type - list, 分类型数据所在的列gamma - float, 分类属性权重。- list, 若为list,保证 len(gamma)==len(Type),每个分类型数据的权重可单独设置"""m, n = data.shape # m:样本数量,n:每个样本的属性值个数result = np.empty(m) # 生成容器,用于存放m个样本的聚类结果cores = data[np.random.choice(np.arange(m), k, replace=False)] # 从m个数据样本中不重复地随机选择k个样本作为质心while True: # 迭代计算distance = get_distances(cores, data, Numerical, Type, gamma) # 计算距离矩阵index_min = np.argmin(distance, axis=1) # 每个样本距离最近的质心索引序号if (index_min == result).all(): # 如果样本聚类没有改变return result, cores # 则返回聚类结果和质心数据result[:] = index_min # 重新分类cores = get_new_cores(result, data, cores) # 重新寻找聚类中心data=pd.read_csv(r'/root/data_tmp/四川未成年人聚类.csv',header=0).values
# data数据共有8列,其中 0-5列的数据为分类型数据,6-7列为数值型数据。
Numerical=[6,7]
Type=[0,1,2,3,4,5]
gamma=[1,1,1,1,1,1,2/7,3/18] # 定义每项指标的占比
k=5 # 设置聚类all_result={} # 用于保存运行结果,保存为json格式
# 运行10
for i in range(10):result, cores = k_prototypes(data, k, Numerical, Type, gamma)all_result[i]={}all_result[i]['result']=result # 保存分类结果all_result[i]['cores'] = cores # 保存分类的簇中心cores_nums=[]for one_k in range(k):cores_nums.append(int(sum(result==one_k))) # 对数据进行转化,后续保存为json格式会报错all_result[i]['cores_nums'] = cores_nums # 保存每个簇的数量3.6 效果评价
import os
import sys
from pyspark import SparkConf
from pyspark.sql import SparkSession
# 如果当前代码文件运行测试需要加入修改路径,避免出现后导包问题
BASE_DIR = os.path.dirname(os.path.dirname(os.getcwd()))
sys.path.insert(0, os.path.join(BASE_DIR))
PYSPARK_PYTHON = "/opt/anaconda3/envs/pythonOnYarn/bin/python3.8"
# 当存在多个版本时,不指定很可能会导致出错
os.environ["PYSPARK_PYTHON"] = PYSPARK_PYTHON
os.environ["PYSPARK_DRIVER_PYTHON"] = PYSPARK_PYTHON
os.environ["HADOOP_USER_NAME"]="hdfs"
spark=SparkSession.builder.master("yarn").appName("chen") \.config("spark.yarn.queue","q2") \.config("spark.executor.instances",80) \.config("spark.executor.cores",8) \.config("spark.executor.memory","4g") \.enableHiveSupport() \.getOrCreate()
sc=spark.sparkContext# 基本参数设置
Numerical=[6,7]
Type=[0,1,2,3,4,5]
k=5
broadcast=sc.broadcast({'k':k,'Num_list':Numerical,'Type_list':Type,'gamma':gamma}) # 广播变量
# 基础数据处理
import pandas as pd
data=pd.read_csv(r'/root/聚类数据.csv',header=0).values
data_list = data.tolist()
data_tuple = [(i, tuple(data_list[i])) for i in range(len(data_list))] # 将数据转化为元组
rdd = sc.parallelize(data_tuple, 75).cache() # 将数据转化为rdd,分区数设为75,
broad_rdd = sc.broadcast(data_tuple) # 将元数据进行广播for key,value in all_result.items(): # all_result 是由之前代码运行的结果result=np.array(value['result']) # 转成ndarray格式cores=np.array(value['cores'])broadresult=sc.broadcast(tuple(result.astype(int).tolist())) # 将当前分类结果进行广播def get_distance_rdd(one_rdd):broadcast_value=broadcast.valuebroadResult=broadresult.valuebroadrdd=broad_rdd.valuedef distance(rdd1,rdd2):sum_=0for i in range(len(rdd1[1])):if i in broadcast_value['Num_list']:sum_+=abs(rdd1[1][i]-rdd2[1][i])*broadcast_value['gamma'][i]elif i in broadcast_value['Type_list']:sum_+=0 if rdd1[1][i]==rdd2[1][i] else broadcast_value['gamma'][i]return sum_cluster_in=[0,0] # [簇内的距离之和,簇内最远距离]cluster_out=[float('inf')]*broadcast_value['k']for one in broadrdd:dis_tmp=distance(one_rdd,one)if broadResult[one[0]] == broadResult[one_rdd[0]]: # 同一簇内cluster_in[0]+=dis_tmpif dis_tmp>cluster_in[1]:cluster_in[1]=dis_tmpelse:if cluster_out[broadResult[one[0]]]>dis_tmp:cluster_out[broadResult[one[0]]]=dis_tmpreturn (broadResult[one_rdd[0]],cluster_in,cluster_out) # (所属类别,(簇内平均距离,簇内最远距离),(不同簇间的最近的距离))res=rdd.map(get_distance_rdd).cache()target=res.map(lambda x:(x[0],x[1]+x[2])).reduceByKey(lambda x,y:[x[0]+y[0],x[1] if x[1]>=y[1] else y[1]]+[x[i] if x[i]<=y[i] else y[i] for i in range(2,len(x))]).sortByKey(ascending=True).collect()avg=[]diam=[]dmin=[]for one in target:avg.append(one[1][0]/(sum(result==one[0])**2))diam.append(one[1][1])dmin.append(one[1][2:])dcen=get_distances(cores, cores, Numerical, Type, gamma).astype(int).tolist()DBI_list=[-float('inf')]*kfor i in range(k):for j in range(k):if i!=j:tmp=(avg[i]+avg[j])/dcen[i][j]if tmp>DBI_list[i]:DBI_list[i]=tmpDBI=sum(DBI_list)/kDI=min([min(one) for one in dmin])/max(diam)all_result[key]['avg']=avgall_result[key]['diam'] = diamall_result[key]['dmin'] = dminall_result[key]['dcen'] = dcenall_result[key]['DBI'] = DBIall_result[key]['DI'] = DI# 将运行结果保存为json文件
import json
def dic_to_json(dic,save_path):tf=open(save_path,"w")json.dump(dic,tf)tf.close()
dic_to_json(all_result,r'/root/k_prototypes_k_5结果.json')相关文章:

人工智能|机器学习——K-means系列聚类算法k-means/ k-modes/ k-prototypes/ ......(划分聚类)
1.k-means聚类 1.1.算法简介 K-Means算法又称K均值算法,属于聚类(clustering)算法的一种,是应用最广泛的聚类算法之一。所谓聚类,即根据相似性原则,将具有较高相似度的数据对象划分至同一类簇,…...
注意力、自注意力和多头注意力的区别
本文作者: slience_me 注意力、自注意力和多头注意力的区别 理解注意力(Attention)、自注意力(Self-Attention)和多头注意力(Multi-Head Attention)之间的区别非常重要,因为它们是自…...

FTP,SFTP,FTPS,SSL,TSL简介,区别,联系,使用场景说明
文章目录 简介FTPFTPSSFTP加密场景选择FTPS还是SFTPFTP、SFTP、FTPS区别、联系和具体使用场景如何使用FTP、SFTP和FTPSSSLTLSSSL和TLS区别和联系,以及使用场景SSL和TLS技术上的区别一些问题隐式的TLS(FTPS/SSL)或者显式的TLS(FTPS…...

路由算法与路由协议
路由选择协议的核心是路由算法,即需要何种算法来获得路由表中的各个项目。 路由算法的目的很简单:给定一组路由器以及连接路由器的链路,路由算法要找到一条从源路由器到目标路由器的最佳路径。通常,最佳路径是指具有最低费用的路…...
dubbo接口自动化用例性能优化
前言 去年换了一个新部门,看了下当前的自动化用例的情况,发现存在三类性能问题: 本地调试运行时等待时间较长,就算是一个简单的case,执行时间都需要1分钟以上单用例执行时间比较长,部分用例执行时间超过2…...

.net core框架
ASP.NET Core 入门 跨平台开源框架 B/S 类与方法 Console 部分称为“类”。 类“拥有”方法;或者可以说方法存在于类中。 WriteLine() 部分称为“方法”。 想要使用方法就要知道方法在哪里 —————————— 执行流 一次执行一段 ASP.NET Core 是什么东西…...
学习大数据,所需要Java基础(9)
文章目录 网络编程实现简答客户端和服务器端的交互编写客户端编写服务端 文件上传文件上传客户端以及服务器端实现文件上传服务器端实现(多线程)文件上传服务器端(连接池版本)关闭资源工具类 BS架构服务器案例案例分析BS结构服务器…...
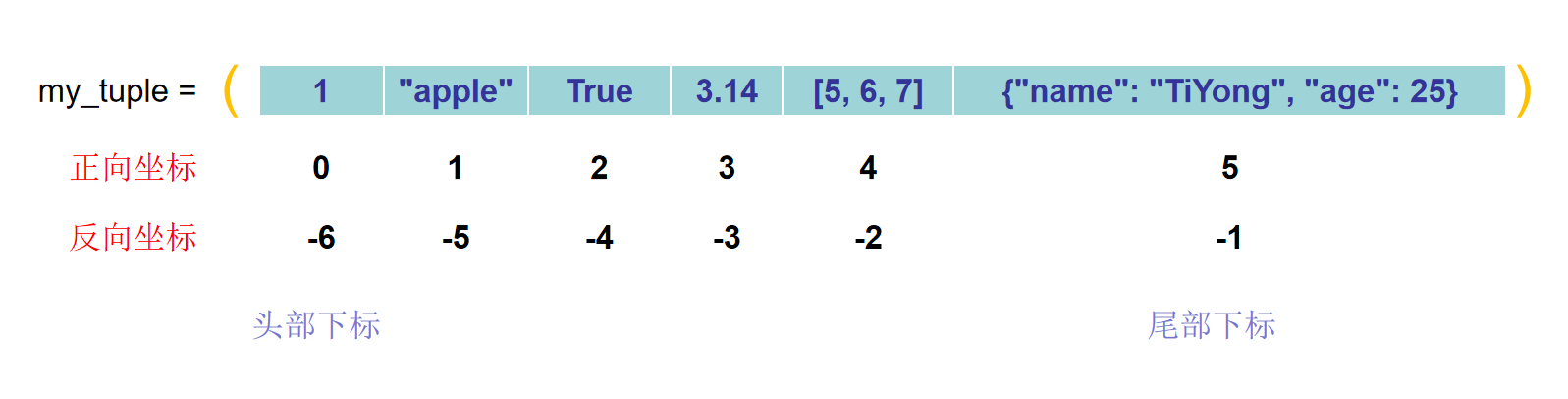
Python元组(Tuple)深度解析!
目录 1. 什么是元组? 2. 创建元组 3.访问元组 4.元组的运算 5.修改元组不可行 6.元组的应用场景 前面的博客里,我们详细介绍了列表(List)这一种数据类型,现在我们来讲讲与列表相似的一种数据类型,元组…...

排序 Comparable接口、Comparator接口
String类的Comparable接口 1、String类实现了Comparable<String>接口,并提供了compareTo方法的实现,因此,字符串对象(即String类型的实例)可以直接调用compareTo()方法来比较它们。2、String类的compareTo()方法…...
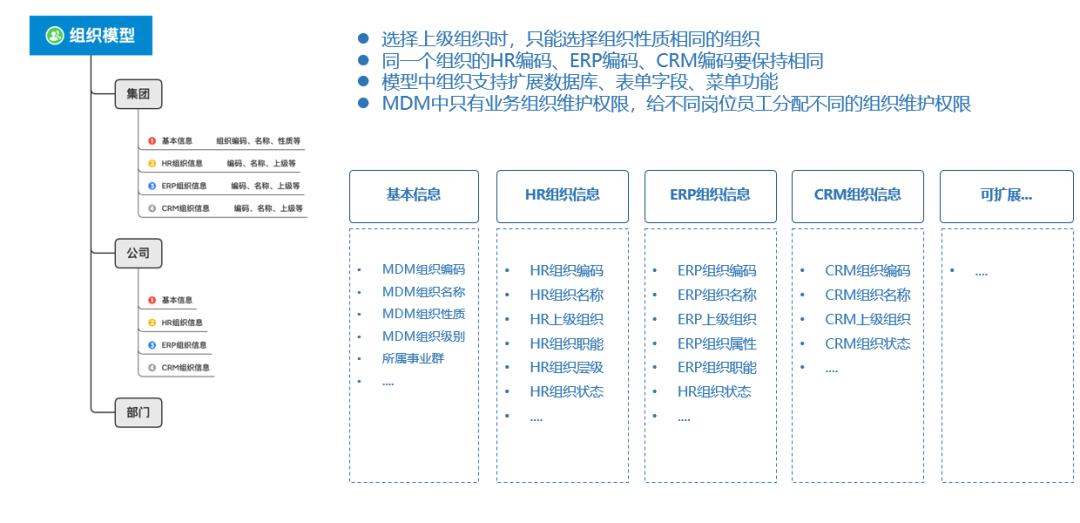
得帆助力大族激光主数据平台建设,用数据为企业生产力赋能
本期客户 大族激光科技产业集团股份有限公司(以下简称“大族激光”)是一家从事工业激光加工设备与自动化等配套设备及其关键器件的研发、生产、销售,激光、机器人及自动化技术在智能制造领域的系统解决方案的优质提供商,是国内激光…...

实名认证电子签署:防范合同纠纷,提升交易信任
当今社会,随着数字化和信息化的发展,电子合同已经成为商务活动中常见的签署方式。而在签署电子合同时进行实名认证,是为了确保合同的真实性、合法性和安全性。本文将从法律、技术和实际应用等方面详细解释为什么签署电子合同需要进行实名认证…...

c++ primer中文版第五版作业第十八章
仓库地址 文章目录 18.118.218.318.418.518.618.718.818.918.1018.1118.1218.1318.1418.1518.16位置一using声明 位置二using声明 位置一using指示 位置二using指示 18.1718.1818.1918.2018.2118.2218.2318.2418.2518.2618.2618.2818.2918.30 18.1 此时r是一个range_error类型…...

vue触发真实的点击 事件 跟用户行为一致
<template><div><button ref"myButton" click"handleClick">按钮</button></div> </template><script> export default {methods: {handleClick() {const button this.$refs.myButton;// 创建一个鼠标点击事件…...

Java进程CPU高负载排查
Java进程CPU高负载排查步骤_java进程cpu使用率高排查_YouluBank的博客-CSDN博客 【问题定位】使用arthas定位CPU高的问题_arthas cpu高_秋装什么的博客-CSDN博客 CPU飙升可能原因 CPU 上下文切换过多。 对于 CPU 来说,同一时刻下每个 CPU 核心只能运行-个线程&…...

Linux编程4.1 网络编程-前导
1、内容概述 网络的基本概念TCP/IP协议概述OSI和TCP/IP模型掌握TCP协议网络基础编程掌握UDP协议网络基础檹网络高级编程 2、计算机联网的目的 使用远程资源共享信息、程序和数据分布处理 3、基本概念 单服务与多客户端的进程间通信C/S client server 由于,跨计…...

【微信小程序】传参存储
目录 一、本地数据存储 wx.setStorage wx.setStorageSync 1.1、异步缓存 存取数据 1.2、同步缓存 存取数据 二、使用url跳转路径携带参数 2.1、 wx.redirectTo({}) 2.2、 wx.navigateTo({}) 2.3、 wx.switchTab({}) 2.4 、wx.reLaunch({}) 2.5、组件跳转 三、…...
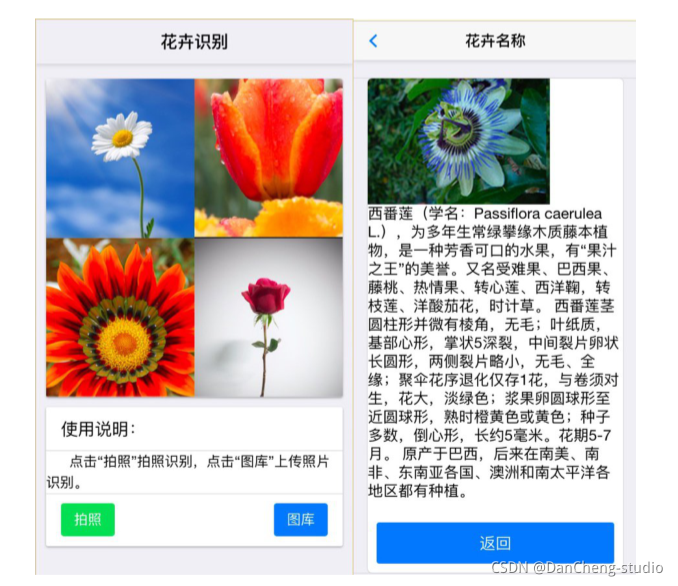
计算机设计大赛 深度学习花卉识别 - python 机器视觉 opencv
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &a…...
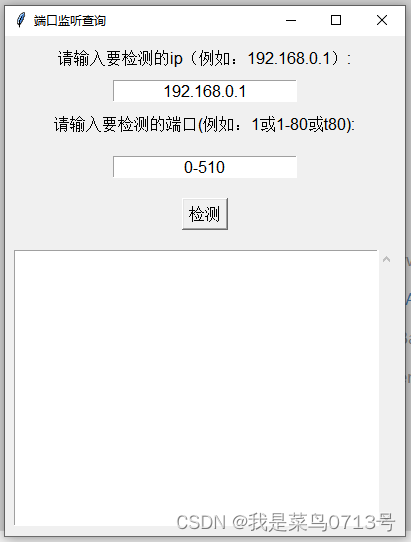
ping多个IP的工具
Ping Tool 项目地址 python开发的IP搜索小工具 ping一个网段所有IP,显示结果查看某个ip地址开放监听的端口配置可保存...

Rust 的 Error 如何使用?
在 Rust 中,错误处理是一个重要且核心的概念。Rust 提供了一种强大的类型系统,允许你明确地处理可能出现的错误。std::error::Error trait 是 Rust 标准库中用于表示错误的基础 trait。实现这个 trait 的类型可以被用作错误类型,并且可以使用…...
Hack The Box-Crafty
目录 信息收集 rustscan whatweb WEB 漏洞利用 漏洞说明 漏洞验证 提权 get user.txt get Administrator 总结 信息收集 rustscan ┌──(root㉿ru)-[~/kali/hackthebox] └─# rustscan -a 10.10.11.249 --range0-65535 --ulimit5000 -- -A -sC [~] Automatically…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
