SCAU 8580 合并链表
8580 合并链表
时间限制:1000MS 代码长度限制:10KB
提交次数:3724 通过次数:2077
题型: 编程题 语言: G++;GCC
Description
线性链表的基本操作如下:
#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
#define ElemType inttypedef int Status;
typedef struct LNode
{int data;struct LNode *next;
}LNode,*LinkList;Status ListInsert_L(LinkList &L, int i, ElemType e) { // 算法2.9// 在带头结点的单链线性表L的第i个元素之前插入元素eLinkList p,s;p = L; int j = 0;while (p && j < i-1) { // 寻找第i-1个结点p = p->next;++j;} if (!p || j > i-1) return ERROR; // i小于1或者大于表长s = (LinkList)malloc(sizeof(LNode)); // 生成新结点s->data = e; s->next = p->next; // 插入L中p->next = s;return OK;
} // LinstInsert_LStatus ListDelete_L(LinkList &L, int i, ElemType &e) { // 算法2.10// 在带头结点的单链线性表L中,删除第i个元素,并由e返回其值LinkList p,q;p = L;int j = 0;while (p->next && j < i-1) { // 寻找第i个结点,并令p指向其前趋p = p->next;++j;}if (!(p->next) || j > i-1) return ERROR; // 删除位置不合理q = p->next;p->next = q->next; // 删除并释放结点e = q->data;free(q);return OK;
} // ListDelete_L设计一个算法将两个非递减有序链表A和B合并成一个新的非递减有序链表C。
输入格式
第一行:单链表A的元素个数
第二行:单链表A的各元素(非递减),用空格分开
第三行:单链表B的元素个数
第四行:单链表B的各元素(非递减),用空格分开
输出格式
第一行:单链表A的元素列表
第二行:单链表B的元素列表
第三行:合并后单链表C的元素列表
输入样例
6
12 24 45 62 84 96
4
15 31 75 86
输出样例
List A:12 24 45 62 84 96
List B:15 31 75 86
List C:12 15 24 31 45 62 75 84 86 96
数组模拟链表
#include<stdio.h>
#include<malloc.h>
#include<iostream>
#include<algorithm>
#define ERROR 0
#define OK 1
#define ElemType int
using namespace std;
int a[100];
int main ()
{int n,m,i;cin>>n;for(i=0;i<n;i++){cin>>a[i];}cout<<"List A:";for(i=0;i<n;i++){cout<<a[i]<<" ";}cin>>m;for(i=n;i<n+m;i++){cin>>a[i];}cout<<endl<<"List B:";for(i=n;i<n+m;i++){cout<<a[i]<<" ";}sort(a,a+n+m);cout<<endl<<"List C:";for(i=0;i<n+m;i++){cout<<a[i]<<" ";}return 0;
}
相关文章:

SCAU 8580 合并链表
8580 合并链表 时间限制:1000MS 代码长度限制:10KB 提交次数:3724 通过次数:2077 题型: 编程题 语言: G;GCC Description 线性链表的基本操作如下: #include<stdio.h> #include<malloc.h> #define ERROR 0 #define OK 1 #define ElemType inttyped…...
Docker安装Gitlab
下载镜像 直接下载最新版,比较大有2.36G docker pull gitlab/gitlab-ce创建数据存放的目录位置 按自己习惯位置创建目录 mkdir -p /usr/local/docker/docker_gitlab编写docker-compose.yml 在上面创建的挂载目录里面(/usr/local/docker/docker_gitl…...

浅淡 C++ 与 C++ 入门
我们知道,C语言是结构化和模块化的语言,适用于较小规模的程序。而当解决复杂问题,需要高度抽象和建模时,C语言则不合适,而C正是在C的基础之上,容纳进去了面向对象编程思想,并增加了许多有用的库…...
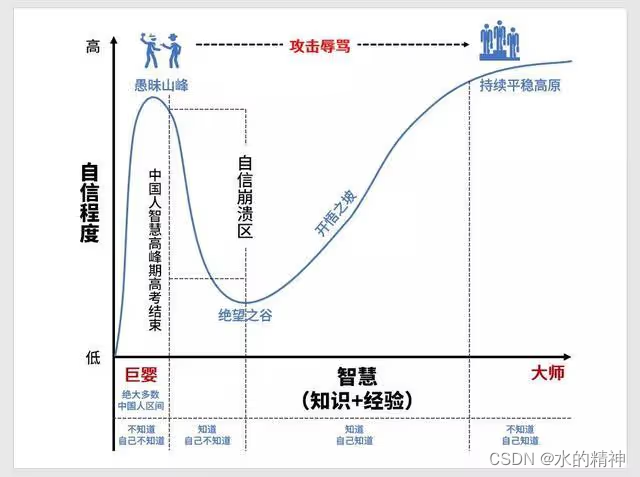
学习和认知的四个阶段,以及学习方法分享
本文分享学习的四个不同的阶段,以及分享个人的一些学习方法。 一、学习认知的四个阶段 我们在学习的过程中,总会经历这几个阶段: 第一阶段:不知道自己不知道; 第二阶段:知道自己不知道; 第三…...
Python编程从入门到实践中的一些误区
1.num 使用num时python报错,后来查过后才知道是因为python不支持自增或自减,可以用1。 2.字符串和非字符串连接 要先将非字符串转换为字符串类型之后才能连接 print(2int(‘2’))#4 3.关键字参数必须在未…...

Kanebo HITECLOTH 高科技擦镜布介绍
Kanebo HITECLOTH,这款由日本KBSeiren公司制造的高科技擦镜布,以其卓越的清洁能力和超柔软的布质,成为了市场上备受瞩目的产品。 材质与特性 HITECLOTH采用0.1旦尼尔特级高级微纤维制造,质地细致、坚韧、不起颗粒。这种纤维的特…...
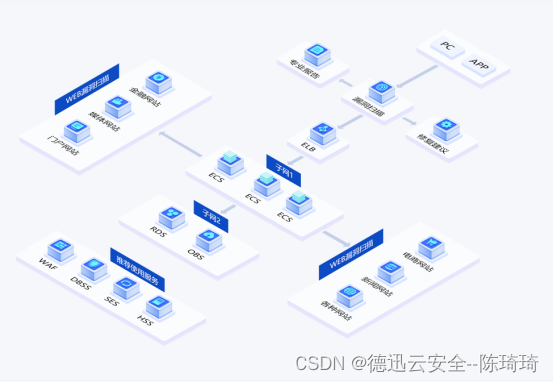
政务云安全风险分析与解决思路探讨
1.1概述 为了掌握某市政务网站的网络安全整体情况,在相关监管机构授权后,我们组织人员抽取了某市78个政务网站进行安全扫描,通过安全扫描,对该市政务网站的整体安全情况进行预估。 1.2工具扫描结果 本次利用漏洞扫描服务VSS共扫…...
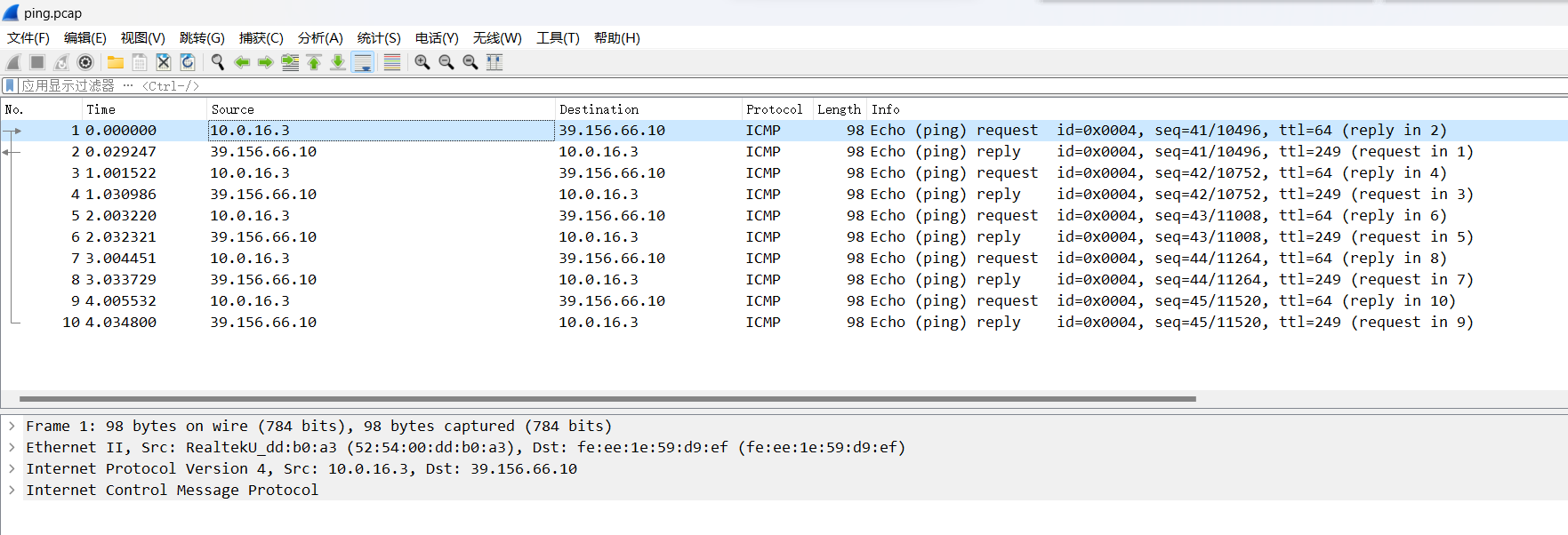
Linux tcpdump抓包转Wireshark 分析
简介 tcpdump 是Linux系统下的一个强大的命令,可以将网络中传送的数据包完全截获下来提供分析。它支持针对网络层、协议、主机、网络或端口的过滤,本文将展示如何使用 tcpdump 抓包,以及如何用 tcpdump 和 wireshark 分析网络流量 tcpdump指…...

【Spring高级】Aware与InitializingBean接口
目录 Aware接口概述为什么需要Aware接口 InitializingBean接口Autoware失效分析 Aware接口 概述 在Spring框架中,Aware 接口是一种常用的设计模式,用于允许bean在初始化时感知(或获取)Spring容器中的某些资源或环境信息。这些接…...

打造你的HTML5打地鼠游戏:零基础入门教程
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...

C++默认构造函数/拷贝构造函数/赋值构造函数
概述 本文主要讲解C默认构造函数,拷贝构造函数和赋值构造函数在哪些场景下会被调用到 代码 类定义 class A{public:A() { cout<<"construct function"<<endl; }A(const A& other) { cout<<"copy construct function"…...

前端框架的发展历史介绍
前端框架的发展历史是Web技术进步的一个重要方面。从最初的简单HTML页面到现在的复杂单页应用程序(SPA),前端框架和库的发展极大地推动了Web应用程序的构建方式。以下是一些关键的前端框架和库,以及它们的发布年份、创建者和主要特…...

Linux 基本命令
文章目录 1.echo2.cd3.find4.mkdir5.cp6.rm7.wc8.tar9.tail10.vim11.grep12.sed13 touch14 ls15 快捷键16 ln17 mv18 useradd19 usermod20 su 每天一个Linux命令 提示:以下是本篇文章正文内容,下面案例可供参考 1.echo 中文 (Chinese): “回声” 或 “输…...
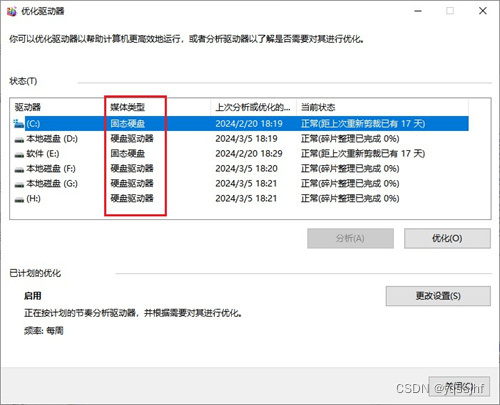
怎么查看电脑是不是固态硬盘?简单几个步骤判断
随着科技的发展,固态硬盘(Solid State Drive,简称SSD)已成为现代电脑的标配。相较于传统的机械硬盘,固态硬盘在读写速度、稳定性和耐用性等方面都有显著优势。但是,对于不熟悉电脑硬件的用户来说࿰…...

在Java中如何优雅的停止一个线程?可别再用Thread.stop()了!
写在开头 经过上几篇博文的学习,我们知道在Java中可以通过new Thread().start()创建一个线程,那今天我们就来思考另外一个问题:线程的终止 自然终止有两种情况: 1. 线程的任务执行完成; 2. 线程在执行任务过程中发生异…...

指数函数与三角函数乘积的积分公式
先上公式,公式正确,用欧拉公式即可证明。 数学公式不好打字,我就发截图。 欧拉公式证明如下:...

代码随想录算法训练营第五九天 | 下一个更大元素II、接雨水
目录 下一个更大元素II接雨水 LeetCode 503.下一个更大元素II LeetCode 42. 接雨水 下一个更大元素II 给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。 数字 x 的 下一…...
算法题_2864_最大二进制奇数)
LeetCode(力扣)算法题_2864_最大二进制奇数
最大二进制奇数 题目描述 给你一个 二进制 字符串 s ,其中至少包含一个 1 。 你必须按某种方式 重新排列 字符串中的位,使得到的二进制数字是可以由该组合生成的 最大二进制奇数 。 以字符串形式,表示并返回可以由给定组合生成的最大二进…...

食药物质创新 赋能中式滋补健康产业发展交流会圆满结束
3月5日,“食药物质创新 赋能中式滋补健康产业发展交流会”在山东国际会展中心召开。本次会议由中国生物发酵产业协会主办,浙江科技大学、未名太研生物科技(绍兴)有限公司承办,汇乐达供应链服务(常州)有限责任公司支持。本次论坛旨在加强行业创…...

用好大模型、承载“头雁领航”使命,央企如何三路出击?
作者 | 曾响铃 文 | 响铃说 智能化成为两会热议话题,2024政府工作报告中也直接提到要深化大数据、人工智能等研发应用,开展“人工智能”行动。 毫无疑问,大模型热潮下,以智能化推进传统产业升级已经成为普遍共识。 具体如何做…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
