C++中using 和 typedef 的区别
C++中using 和 typedef 的区别_typedef using-CSDN博客
在C++中,“using”和“typedef”执行声明类型别名的相同任务。两者之间没有重大区别。C++中的“Using”被认为是类型定义同义词。此方法也称为别名声明。定义这些别名声明的工作方式类似于使用“using”语句定义C++中的变量。它有助于提高代码的整体可读性。与“typedef”语句不同,C++中的“using”能够创建别名模板,从而为基础类型提供功能。通过在C++代码中使用“using”,可以具有相同抽象级别的常用类型别名,并且可以在将来指定模板参数。
C++中的“Typedef”执行别名定义的类似任务。它基本上引入了一个名称,该名称使用该范围内的类型声明成为给定类型的同义词。“typedef”的一个重要特性是,它允许程序员封装可能随时间变化的实现细节。在C++中,typedef提供了'using'语句的所有功能,除了不允许使用对编码角度非常有用的模板。'typedef' 声明不像 union、enum、class 等那样引入新类型。相反,它们为已存在的类型提供新名称。这些新名称与其他标识符占用相同的命名空间。
- C++中 using 语句和 typedef 语句之间的主要区别之一是,“using”可以执行 “typedef” 可以执行的所有任务。
- 从程序员的角度来看,使用“using”语句非常容易和清晰,尤其是在使用函数指针及其别名定义时。事实上,'using'语句为代码提供了更高的可读性,如下面的示例所示:
typedef void(*func_pointer)(int);
vs
using func_pointer = void(*)(int);相关文章:

C++中using 和 typedef 的区别
C中using 和 typedef 的区别_typedef using-CSDN博客 在C中,“using”和“typedef”执行声明类型别名的相同任务。两者之间没有重大区别。C中的“Using”被认为是类型定义同义词。此方法也称为别名声明。定义这些别名声明的工作方式类似于使用“using”语句定义C中…...
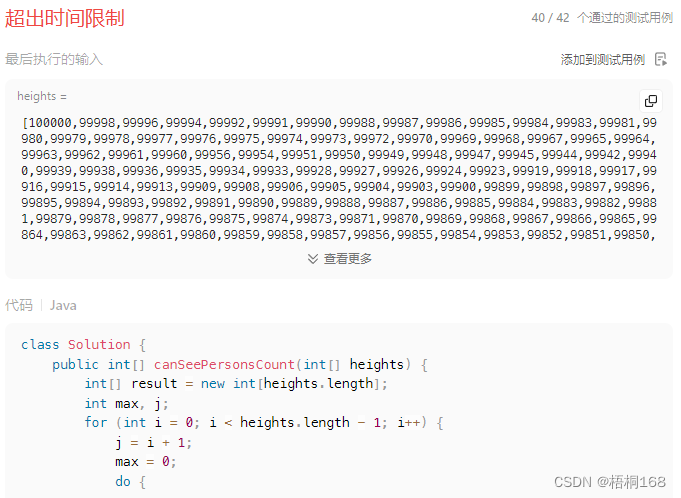
LeetCode-1944题: 队列中可以看到的人数(原创)
【题目描述】 有 n 个人排成一个队列,从左到右 编号为 0 到 n - 1 。给你以一个整数数组 heights ,每个整数 互不相同,heights[i] 表示第 i 个人的高度。一个人能 看到 他右边另一个人的条件是这两人之间的所有人都比他们两人 矮 。更正式的&…...

Java基础面试题整理2024/3/13
1、可以使用switch的数据类型 Java5以前,switch(arg)表达式中,arg只能是byte、short、char、int。 Java5之后引入了枚举类型,也可以是枚举类型。 Java7开始引入了字符串类型。 2、Java中的goto有什么作用 goto是Java中的保留字,…...

MachineSink - 优化阅读笔记
注:该优化与全局子表达式消除刚好是相反的过程,具体该不该做这个优化得看代价模型算出来的结果(有采样文件指导算得会更准确) 该优化过程将指令移动到后继基本块中,以便它们不会在不需要其结果的路径上执行。 该优化过程并非旨在替代或完全…...

虾皮shopee根据ID取商品详情 API
公共参数 名称类型必须描述keyString是免费申请调用key(必须以GET方式拼接在URL中)secretString是调用密钥api_nameString是API接口名称(包括在请求地址中)[item_search,item_get,item_search_shop等]cacheString否[yes,no]默认y…...

你知道数据库有哪些约束吗?
目录 1. NULL约束 2. 唯一(UNIQUE)约束 3. 默认值(DEFAULT)约束 4. 主键约束 5. 外键约束 6. CHECK约束 数据库约束是一种用于确保数据库中数据完整性和一致性的规则或条件。这些约束可以应用于表、列或整个数据库࿰…...
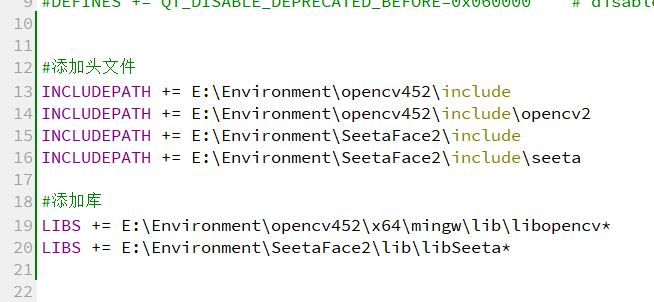
QT----基于QT的人脸考勤系统(未完成)
目录 1 编译opencv库1.1 下载源代码1.2 qt编译opencv1.3 执行Cmake一直卡着data: Download: face_landmark_model.dat 2 编译SeetaFace2代码2.1 遇到报错By not providing "FindOpenCV.cmake" in CMAKE_MODULE_PATH this project has2.2遇到报错Model missing 3 测试…...
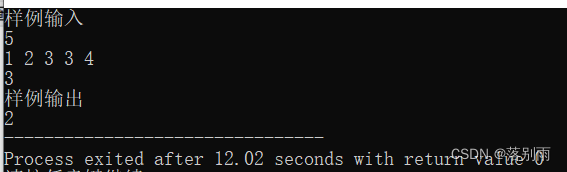
机试:成绩排名
问题描述: 代码示例: #include <bits/stdc.h> using namespace std;int main(){cout << "样例输入" << endl; int n;int m;cin >> n;int nums[n];for(int i 0; i < n; i){cin >> nums[i];}// 排序for(int i 0; i < n; i){//…...

C编程基础四十分笔记
都是一些基础的C语言 一 输入一个整数,计算这个整数有几位二 编写程序计算一个分布函数三 输入一个字符串,再随便输入一个字母,判断这个字母出现几次四 求 1到10的阶乘之和五 求一个球体体积六 写一个链表,存1,2&#…...

k8s关于pod
目录 1、POD 的创建流程 kubectl 发起创建 Pod 请求: API Server 接收请求并处理: 写入 Etcd 数据库: Kubelet 监听并创建 Pod: Pod 状态更新和汇报: 2、POD 的状态解析 1. Pending Pod 2. Running Pod 3. S…...
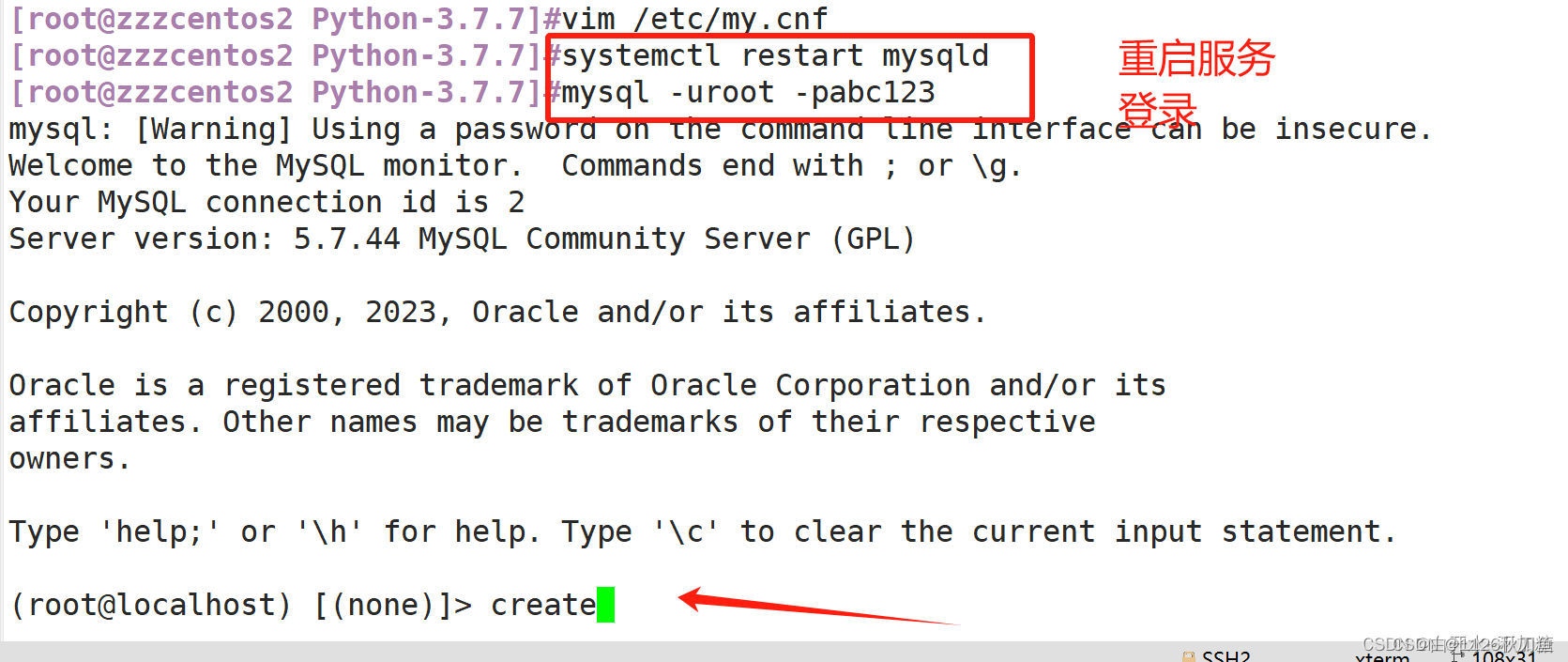
yum安装mysql 数据库tab自动补全
centos7上面没有mysql,它的数据库名字叫做mariadb [rootlocalhost ~]#yum install mariadb-server -y [rootlocalhost ~]#systemctl start mariadb.service [rootlocalhost ~]#systemctl stop firewalld [rootlocalhost ~]#setenforce 0 [rootlocalhost ~]#ss -na…...
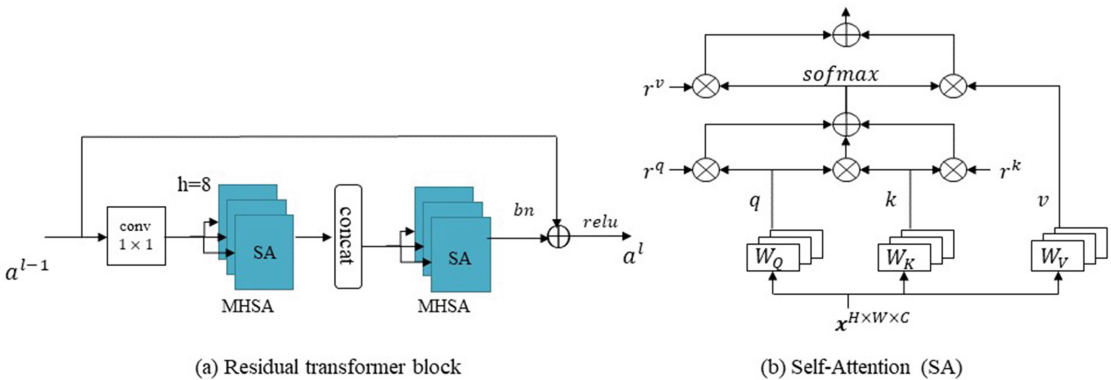
MBT-Net
feature F,edge feature E-F where r related to the relative position 辅助信息 作者未提供代码...

大数据赋能,能源企业的智慧转型之路
在数字洪流中,大数据已经成为推动产业升级的新引擎。特别是在能源行业,大数据的应用正引领着一场深刻的智慧转型。今天,我们就来探讨大数据如何在能源企业中发挥其独特的魅力,助力企业提效降本,实现绿色发展。 动态监控…...

2024考研国家线公布,各科分数线有哪些变化?考研国家线哪些涨了,哪些跌了?可视化分析告诉你
结论在文章结尾 2024考研国家线 一、近五年国家线趋势图-学术硕士 文学 管理学 工学照顾专业 体育学 交叉学科 军事学 历史学 理学 享受少数名族照顾政策的考生 中医类照顾专业 教育类 艺术类 医学 工学 哲学 法学 农学 经济学 二、近五年国家线趋势图-专业硕士 中医 应用心理 …...

高效、安全的APP分发与推广平台
在信息化快速发展的今天,APP已经成为人们生活中不可或缺的一部分。然而,对于众多APP开发者来说,如何让自己的APP在众多竞争者中脱颖而出,被更多用户所认知和下载,成为了一个亟待解决的问题。这时,一个高效、…...

浅谈异或运算
异或,是一个数学运算符,英文为exclusive OR,缩写为xor,应用于逻辑运算。异或的数学符号为“⊕”,计算机符号为“xor”。其运算法则为: a⊕b (a ∧ b) ∨ (a ∧b…...

Linux下platform总线
一. 简介 前面我们讲了设备驱动的分离,并且引出了总线 (bus) 、驱动 (driver) 和设备 (device) 模型,比如 I2C 、 SPI 、 USB 等总线。 但是,在 SOC 中有些外设是没有总线这个概念的,但是又要使用总 线、驱动和设备模型该怎么…...
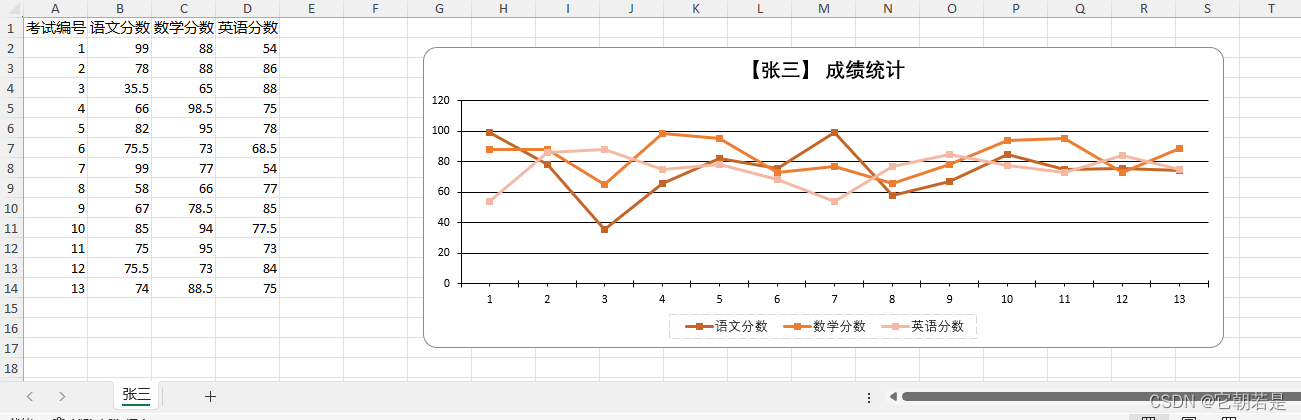
C# EPPlus导出dataset----Excel2绘制图像
一、生成折线图方法 /// <summary> ///生成折线图 /// </summary> /// <param name="worksheet">sheet页数据 </param> /// <param name="colcount">总列数</param> /// &l…...
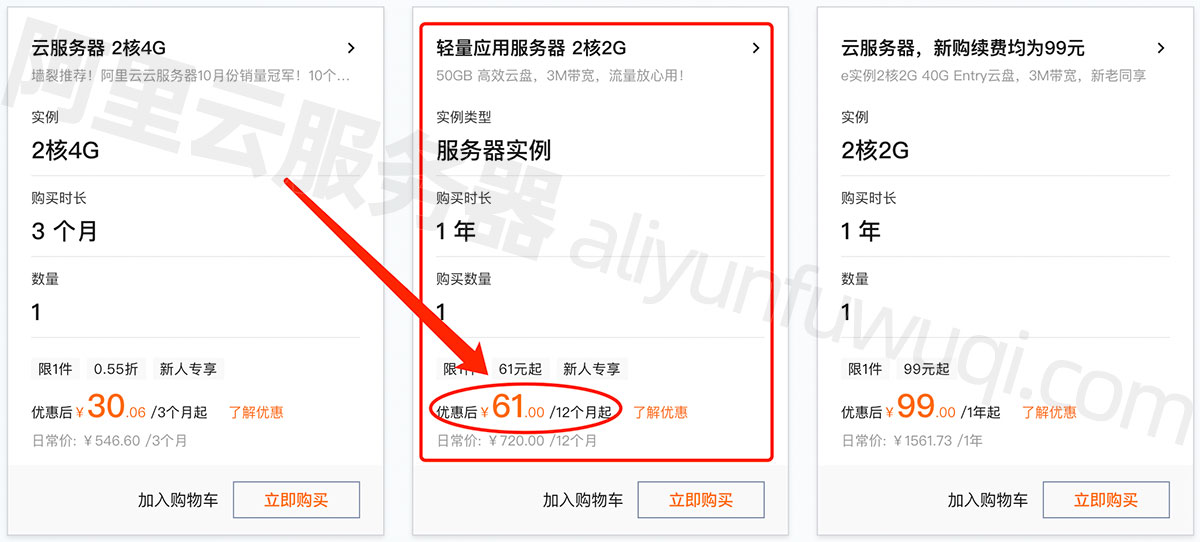
2024年云服务器ECS价格表出炉——阿里云
2024年阿里云服务器租用费用,云服务器ECS经济型e实例2核2G、3M固定带宽99元一年,轻量应用服务器2核2G3M带宽轻量服务器一年61元,ECS u1服务器2核4G5M固定带宽199元一年,2核4G4M带宽轻量服务器一年165元12个月,2核4G服务…...

Grafana
介绍 官网:https://grafana.com/ Grafana 是一个开源的指标分析和可视化工具,它被广泛用于展示和监控云基础设施和应用程序的实时数据。Grafana 提供了一个强大且易于使用的界面,允许用户创建各种图表、图形和仪表盘,以直观地展…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...
