滑模控制(Sliding mode control)快速入门
0. 简介
最近作者受到邀请,让我帮忙给刚入门的学弟讲讲滑模控制。可是作者也不知道怎么向未入门的学弟讲解这些基础知识,所以作者翻了翻近几年写的很好的文章以及视频。综合起来,来总结出一套比较基础,且适用于初学者的文章吧。这里我们先贴一下王崇卫同学的笔记。

对应的视频连接在下面:
【Advanced控制理论】17
1. 滑模控制目的
对于滑模控制而言,我觉得我们先要明白其目的再来学习。一开始我们对滑动控制的定义是:滑动模式是先使用受控系统产生两个以上的子系统,然后再刻意加入一些切换条件产生滑动模式,以达成控制目标的一种技术。
滑模控制(sliding mode control, SMC)也叫变结构控制,其本质上是一类特殊的非线性控制,且非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的“结构”并不固定,而是可以在动态过程中,根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动。
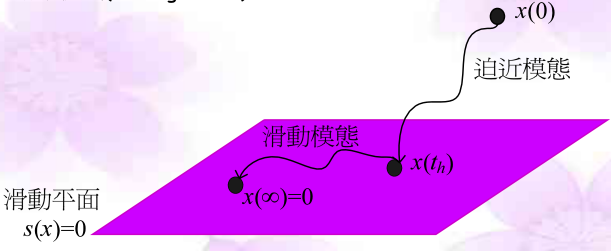
例如滑动模式控制中存在滑动曲面s=0s=0s=0,一开始时,系统会在有限时间内到达滑动曲面,之后就会沿着滑动曲面移动。在滑动模式的理论叙述中,系统会约束在滑动曲面上,因此只需将系统视为在滑动曲面上滑动。不过实际系统的实现是用高频切换来让系统近似在滑动曲面上滑动,高频切换的控制信号让系统在很邻近滑动曲面的范围内切跳(chatter),而且其频率是不固定的。虽然整体系统是非线性的,不过下图中,当系统到达滑动曲面后,理想(没有切跳)系统会限制在s=0s=0s=0的滑动曲面上,滑动曲面是线性时不变系统,在原点处指数稳定。
2. 滑模控制优缺点
2.1 滑模控制的优点:
滑动模态可以设计且与对象参数和扰动无关,具有快速响应、对参数变化和扰动不灵敏( 鲁棒性)、无须系统在线辨识、物理实现简单。
2.2 滑模控制的缺点:
当状态轨迹到达滑动模态面后,难以严格沿着滑动模态面向平衡点滑动,而是在其两侧来回穿越地趋近平衡点,从而产生抖振——滑模控制实际应用中的主要障碍。国内外主要通过改进滑模趋近律达到减弱抖振的目的。
3. 滑模控制需要条件
上文讲到滑模变结构控制器设计也包括两部分,一是能从状态空间的任何位置有限时间到达滑模面 s=0s = 0s=0,二是在滑模面上可以收敛到原点(平衡点)。这也就代表我们要存在有一个稳定的滑模面,且该滑模面是可达的。为此有以下四个条件:
- 稳定性条件:在s=0的滑模面上,状态是收敛的,即滑动模态存在;
- 可达性条件:在切换面s=0以外的运动点将于有限时间内到达切换面;
- 保证滑模运动的稳定性;
- 达到控制系统运动品质要求。
下面将按照四个条件来叙述如何设计滑模控制的控制器,这里的部分内容借鉴了文章滑动模型控制(Sliding Mode Control),并结合作者的理解进行写作。
3.1 被控系统的滑模面生成
首先第一步就是我们需要明白,我们需要找到一个滑模面来让被控系统在滑模面上维持稳定。
例如假设存在一个被控系统:
x˙1=x2x˙2=u\begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= u \end{aligned}x˙1x˙2=x2=u
这个时候我们就需要根据被控系统设计一个滑模面,滑模面一般可以设计为如下的形式
s(x)=∑i=1n−1cixi+xns(x) = \sum_{i=1}^{n-1} c_i x_i + x_ns(x)=i=1∑n−1cixi+xn
因为在滑模控制中,要保证多项式pn−1+cnpn−2+⋯+c2p+c1p^{n − 1} + c_n p^{n − 2} + \cdots + c_2 p + c_1pn−1+cnpn−2+⋯+c2p+c1为Hurwitz (简单来说这条条件是为了满足状态在s=0s=0s=0的滑模面上可以收敛)。
什么是Hurwitz,即上述多项式的特征值的实数部分在左半平面,即为负。
我们可以看到上述的被控系统是存在有两个变量,所以需要取n=2n=2n=2,即 s(x)=c1x1+x2s ( x ) = c_1 x_1 + x_2s(x)=c1x1+x2,为了保证多项式 p+c1p+c_1p+c1为Hurwitz,需要多项式p+c1=0p+c_1=0p+c1=0的特征值实数部分为负,即c1>0c_1>0c1>0。
我们知道滑模控制需要使得状态x1x_1x1 和x2x_2x2的导数均达到零,我们令 s=0s=0s=0,分析一下结果有
{cx1+x2=0x˙1=x2⇒cx1+x˙1=0⇒{x1(t)=e−ctx1(0)x2(t)=x˙1(t)=−cx1(0)e−ct\left\{\begin{aligned} &cx_1 + x_2 = 0 \\ &\dot{x}_1 = x_2 \end{aligned}\right. ~~ \Rightarrow ~~ c x_1 + \dot{x}_1 = 0 ~~ \Rightarrow ~~ \left\{\begin{aligned} &x_1(t) = \text{e}^{-ct} x_1(0) \\ &x_2(t) = \dot{x}_1(t) = -c x_1(0) \text{e}^{-ct} \end{aligned}\right.{cx1+x2=0x˙1=x2 ⇒ cx1+x˙1=0 ⇒ {x1(t)=e−ctx1(0)x2(t)=x˙1(t)=−cx1(0)e−ct
通过上式可以看到状态x1x_1x1 和 x2x_2x2 最终都是趋向于零的,而且速度是以指数速率趋紧的。指数速率意味着当t=1/ct=1/ct=1/c时,趋零过程完成63.2%63.2\%63.2%,当t=3/ct=3/ct=3/c时,趋零过程完成 95.021%95.021\%95.021%。那么我们通过调节参数ccc的大小即可实现对趋零速度的调节,ccc 越大,速度越快。
因此如果满足了 s=cx1+x2=0s=cx_1 + x_2=0s=cx1+x2=0,那么系统的状态x1x_1x1 和x2x_2x2也将沿着滑模面趋近于零 (s=0s=0s=0称之为滑模面)。
3.2 可达性控制器设计
在拿到滑模面后则证明被控系统的稳定性条件成立,下面一步就是可达性条件,即状态xxx 从状态空间中任意一点出发,可以在有限时间到达 s=0s=0s=0 的滑模面上,此时我们可以采用李雅普诺夫间接法来分析,从前面可知,切换函数 sss 是状态变量 xxx 的函数,取以下的李雅普诺夫函数
V=12s2V = \frac{1}{2} s^2V=21s2
对时间求导可得
V˙=ss˙=s(−sgn(s)−s)=−sgn(s)s−s2=−(∣s∣+s2)<0\begin{aligned} \dot{V} &= s \dot{s} \\ &= s (-\text{sgn}(s) - s) \\ &= -\text{sgn}(s) s - s^2 \\ &= -(|s| + s^2) < 0 \end{aligned}V˙=ss˙=s(−sgn(s)−s)=−sgn(s)s−s2=−(∣s∣+s2)<0
为了使系统稳定,我们需要使V˙<0\dot{V}<0V˙<0,即 ss˙<0s \dot{s}<0ss˙<0。此时系统对于 sss而言是渐进稳定,不能保证其有限时间到s=0s=0s=0 的滑模面上(渐进稳定是当 ttt趋于无穷时,状态变量 xxx 趋于 000,即无限时间到达),因此需要 ss˙<−σs \dot{s}<-\sigmass˙<−σ,σ\sigmaσ是一个极小的正数。以上就是可达性条件成立的必要依据\color{red}{以上就是可达性条件成立的必要依据}以上就是可达性条件成立的必要依据。
但是实际上每次设计总不能都用李雅普诺夫函数判断,于是人们就提出了趋近律这一概念,常用的趋近律有如下几种,其中sgn(s)\text{sgn}(s)sgn(s) 是符号函数, s>0,sgn(s)=1;s<0,sgn(s)=−1;s=0,sgn(s)=0s>0,\text{sgn}(s)=1; s<0, \text{sgn}(s)=-1; s=0, \text{sgn}(s)=0s>0,sgn(s)=1;s<0,sgn(s)=−1;s=0,sgn(s)=0:
-
等速趋近律: s˙=−ϵsgn(s),ϵ>0\dot{s} = -\epsilon ~\text{sgn}(s), ~~~~\epsilon > 0s˙=−ϵ sgn(s), ϵ>0
-
指数趋近律:s˙=−ϵsgn(s)−ks,ϵ>0,k>0\dot{s} = -\epsilon ~\text{sgn}(s) - k s, ~~~~\epsilon > 0, k>0s˙=−ϵ sgn(s)−ks, ϵ>0,k>0
-
幂次趋近律: s˙=−k∣s∣αsgn(s)−ks,k>0,0<α<1\dot{s} = -k |s|^\alpha ~\text{sgn}(s) - k s, ~~~~k>0, 0<\alpha<1s˙=−k∣s∣α sgn(s)−ks, k>0,0<α<1
一般在使用时候我们需要完成这些参数的调整,一般我们使用的是指数趋近率,并将ϵ\epsilonϵ和kkk的值均设为1,简化为:
s˙=sgn(s)−s\dot{s} = ~\text{sgn}(s) - ss˙= sgn(s)−s
然后我们可知s(x)=c1x1+x2s ( x ) = c_1 x_1 + x_2s(x)=c1x1+x2,则s˙=sgn(s)−s=c1x1˙+x2˙=c1x2+u\dot{s} = ~\text{sgn}(s) - s = c_1 \dot{x_1} + \dot{x_2} = c_1x_2+us˙= sgn(s)−s=c1x1˙+x2˙=c1x2+u。则我们可以得到控制器uuu为:
u=sgn(s)−s−c1x2u = ~\text{sgn}(s) - s - c_1x_2u= sgn(s)−s−c1x2
这就得到了我们必要的两个条件即,存在滑模面sss以及可达性控制器uuu.
4. 滑模控制Python代码
下面是最简单的python代码
…详情请参照古月居
相关文章:

滑模控制(Sliding mode control)快速入门
0. 简介 最近作者受到邀请,让我帮忙给刚入门的学弟讲讲滑模控制。可是作者也不知道怎么向未入门的学弟讲解这些基础知识,所以作者翻了翻近几年写的很好的文章以及视频。综合起来,来总结出一套比较基础,且适用于初学者的文章吧。这…...
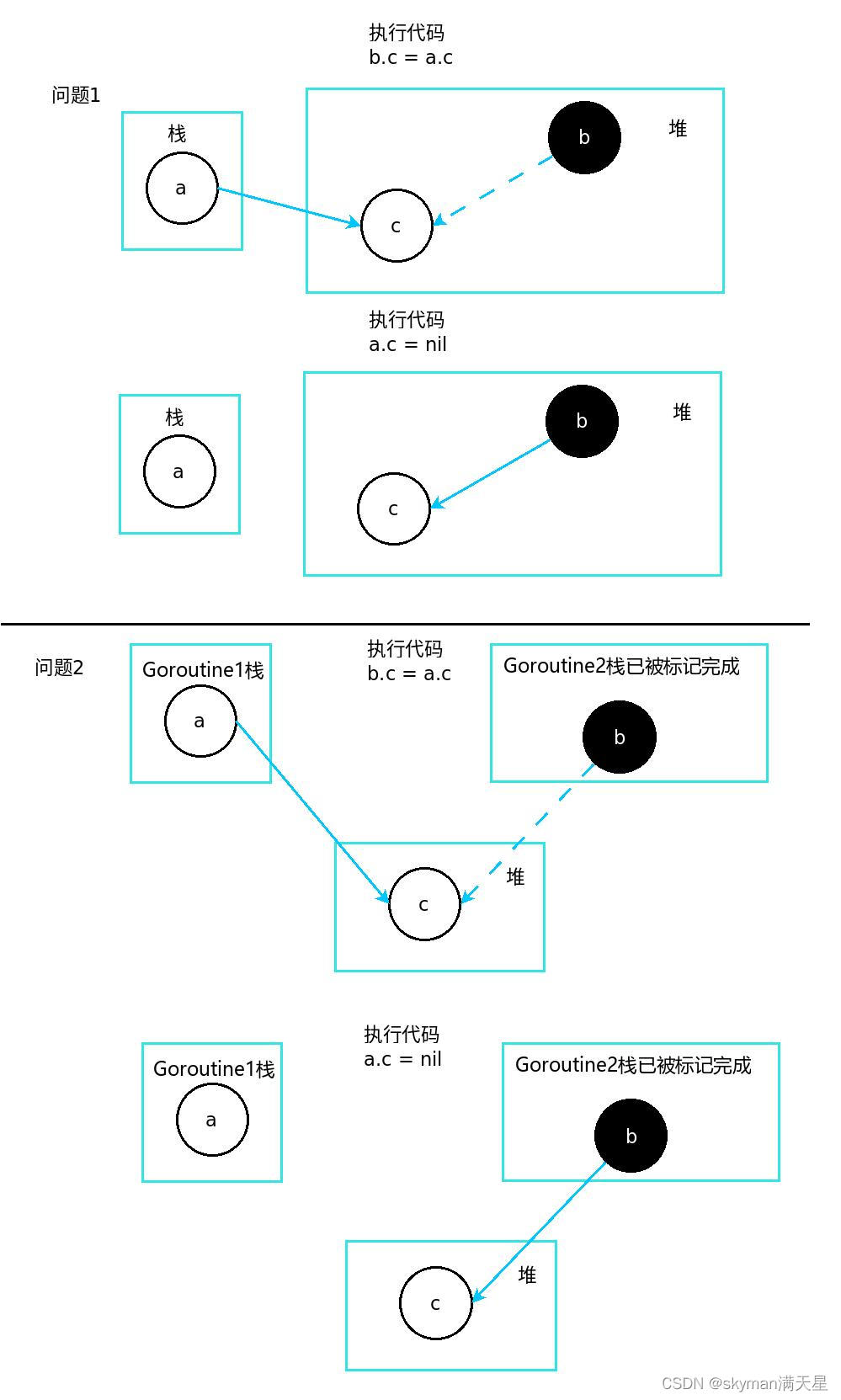
golang的垃圾回收详解
golang的垃圾回收详解 一、三色标记法 作为一门现代化的语言,golang与java一样,都在语言中内置了垃圾回收的功能,不需要程序员自己去回收堆内存。而垃圾回收中,最重要的两个部分就是垃圾检测算法以及垃圾回收算法。垃圾检测算法决…...
线上负载过高排查(top/vmstat/ifstat/free/df)
目录 一、五大命令 二、故障排查步骤 1、top命令找出CPU占比最高的 2、ps -ef 或者 jps -l进一步定位 3、ps -mp位到具体线程或者代码 4、jstack精准定位到错误的地方 本文通过学习:周阳老师-尚硅谷Java大厂面试题第二季 总结的LinuxJDK命令操作相关的笔记 一…...
Java的注解(Annotation)
Java 注解(Annotation)又称 Java 标注,是 JDK5.0 引入的一种注释机制。Java 中的类、构造器、方法、成员变量、参数等都可以被注解进行标注。例如JUnit单元测试中的Test方法,可以使得方法直接运行。JUnit单元测试Test单元测试是针…...

信息系统项目管理师:配置管理
配置管理指的是在一个系统或软件中对配置项的管理,包括对配置项的定义、存储、跟踪和修改等一系列活动。配置项可以是硬件设备、软件组件、系统设置、网络配置等,配置管理旨在确保在不同时间点或环境下系统或软件的配置项的正确性和一致性。通过配置管理…...
web餐饮开源程序
简介 一款专门针对餐饮行业而开发桌面应用程序 技术 借助Panuon.UI.Silver控件库,开发的一款餐饮软件。 运行环境:.NETFramework,Versionv4.8。 运行数据库:MySql。 ORM框架:SqlSugar。 第三方插件:Panuon.UI.Silv…...
28个案例问题分析---027---单表的11个Update接口--MyBatis
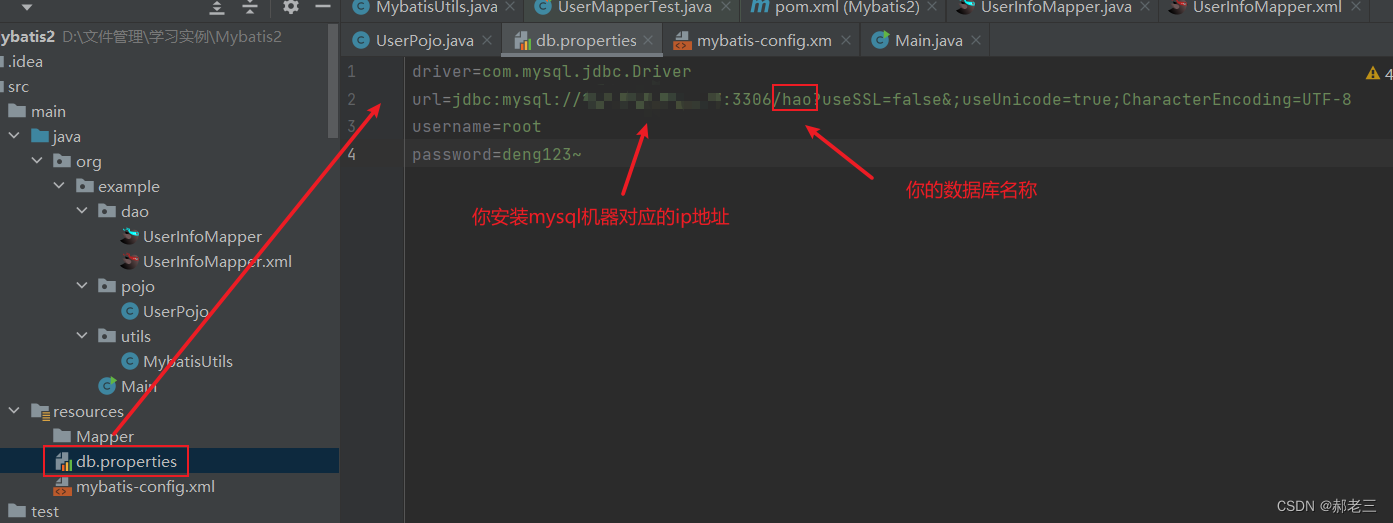
一:背景介绍 项目开发中。我们使用的是MyBatis,在MyBatis的xml文件里,两个表的更新功能,写了足足11个更新接口,毫无复用的思想 这种方式可以正常的实现功能,但是没有复用,无论是从时间上还是维…...

大数据开发治理平台 DataWorks
序言学习下阿里DataWorks的设计理念以及要做的事情cuiyaonan2000163.com参考文档:https://www.aliyun.com/product/bigdata/idehttps://help.aliyun.com/document_detail/73015.htmlhttps://help.aliyun.com/document_detail/324149.html ----数据治理LaunchDataWorks基于阿里云…...

Xshell的下载、使用、配置【ssh、telnet、串口】
目录 一、概述 二、Xshell的使用 2.1 Xshell使用ssh协议远程连接Linux主机或服务器 2.2 Xshell使用telnet协议远程连接Linux开发板 2.3 Xshell使用SERIAL协议远程连接Linux开发板 三、Xshell常用配置 3.1 配置默认会话属性 一、概述 Xshell是由NetSarang公司开发的强大…...
C++回顾(七)—— 面向对象模型
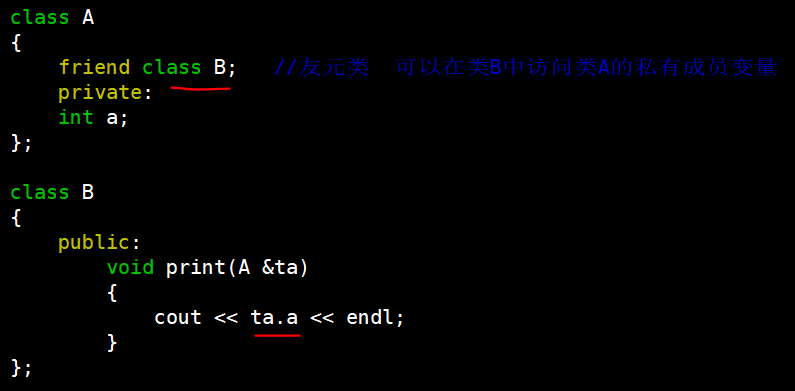
7.1 静态成员变量和静态成员函数 7.1.1 静态成员变量 关键字 static 可以用于说明一个类的成员;静态成员提供了一个同类对象的共享机制;把一个类的成员说明为 static 时,这个类无论有多少个对象被创建,这些对象共享这个 static …...

开源监控服务uptime-kuma
好久没写文章了,刚好最近用了一个开源的监控服务,感觉蛮有意思的,记录一下 (一)安装 uptime-kuma安装方式有几种,这里当然是选择大家都爱的docker,一条命令搞定 docker run -d --restartalways -p 3001:…...

JavaScript混淆技术:了解其核心原理和常用手段
当今互联网时代,JavaScript已经成为了web前端开发的重点技术之一。其中,JavaScript代码的安全性问题一直是关注的焦点。为了保护JavaScript代码的安全性,很多人对其进行加密处理,众所周知,对于单纯的加密算法ÿ…...

大型医院云HIS系统:采用前后端分离架构,前端由Angular语言、JavaScript开发;后端使用Java语言开发 融合B/S版电子病历系统
一套医院云his系统源码 采用前后端分离架构,前端由Angular语言、JavaScript开发;后端使用Java语言开发。融合B/S版电子病历系统,支持电子病历四级,HIS与电子病历系统均拥有自主知识产权。 文末卡片获取联系! 基于云计…...
SAP UI5 Upload/Download file through NetWeaver Gateway
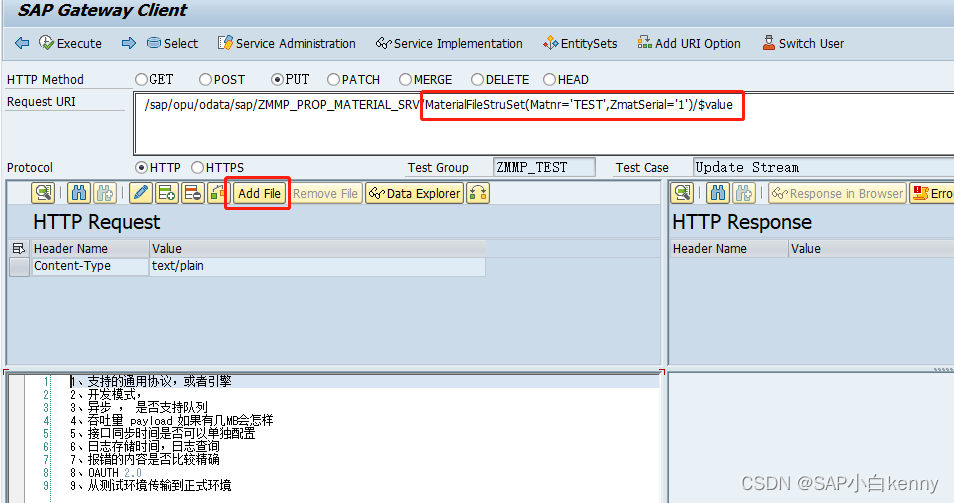
1、创建 SEGW对象 2、创建Entity Type 要把Media 标识打上 3、 激活对象然后到DPC Class的扩展对象里面重定义 /IWBEP/IF_MGW_APPL_SRV_RUNTIME~GET_STREAM /IWBEP/IF_MGW_APPL_SRV_RUNTIME~CREATE_STREAM /IWBEP/IF_MGW_APPL_SRV_RUNTIME~UPDATE_STREAM METHOD /iwbep/if_m…...
opencv校正图像
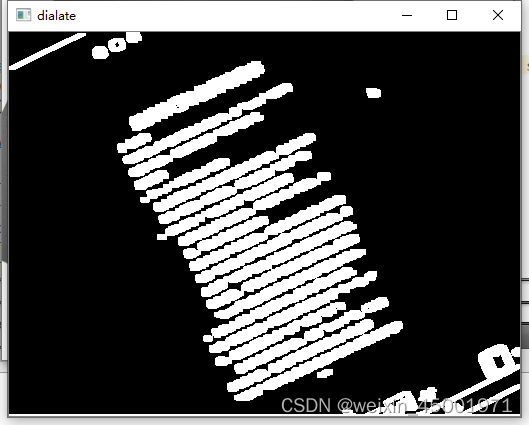
目录1、前言2、例程2.1、代码2.2、效果口罩说明书网页3、按步骤分析转灰度图降噪 Canny边缘检测膨胀(可视具体情况省略)轮廓检索选取角度1、前言 我们用相机拍照时,会因为角度问题造成拍歪,会影响图像的识别,这时就需…...

JavaScript:函数与箭头函数的区别
ref 1. 定义 函数 function getName() {}箭头函数 const getName () > {}2. 命名 函数分为匿名、具名。 function getName() {} let getName function () {}箭头函数只有匿名。 const getName () > {}3. 构造函数 箭头函数都是匿名函数,所以不能作为构造…...
)
八股文(四)
目录 一、 Vue2的双向数据绑定原理 二、 vue2数据绑定缺点是什么?vue3是怎么解决的? (1)因为vue2.0 object.defineProperty只能劫持对象属性 (2)Proxy是直接代理对象 (3)proxy不…...
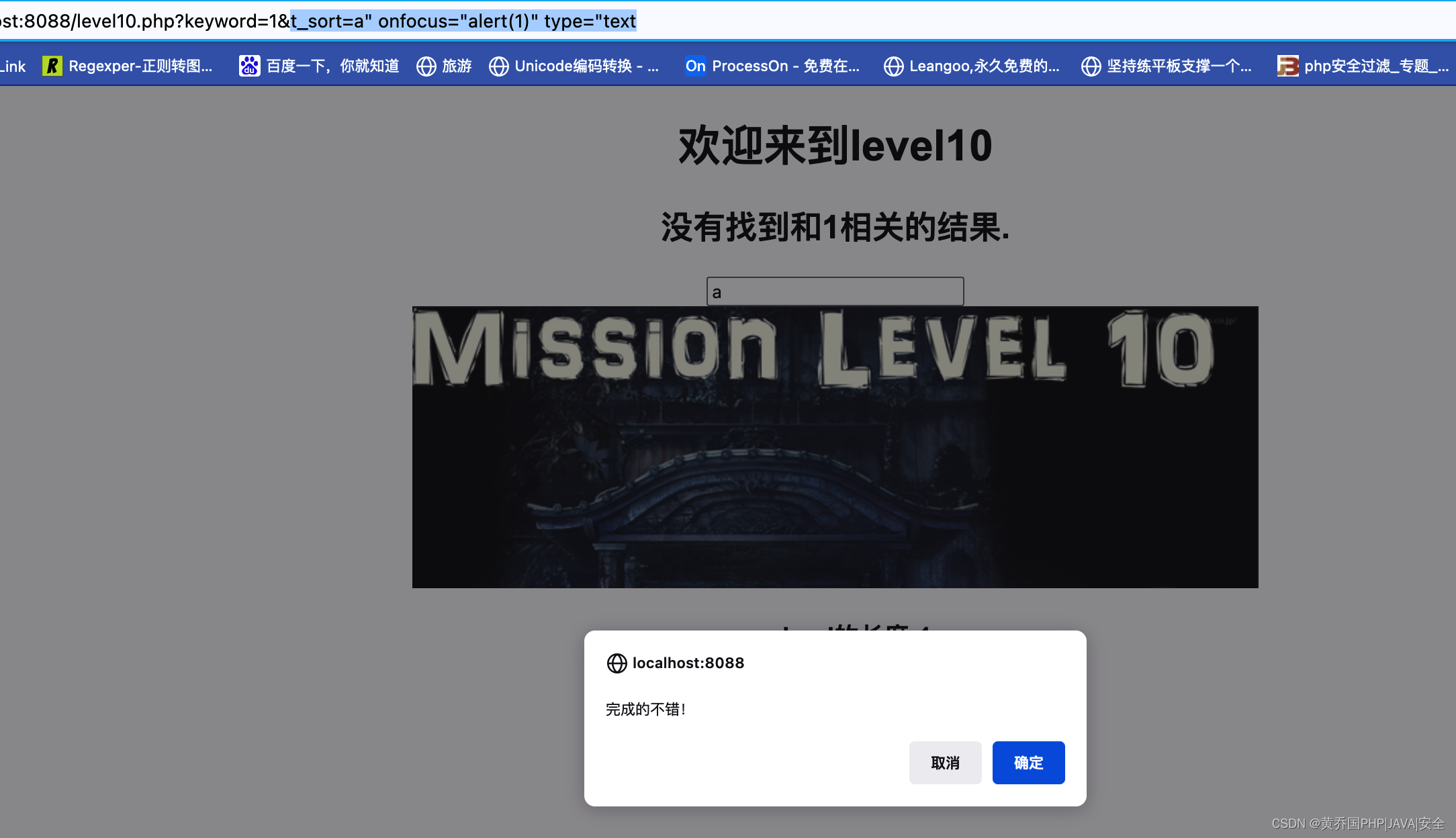
XSS挑战赛(xsslabs)1~10关通关解析
简介 XSS挑战赛,里面包含了各种XSS的防御方式和绕过方式,好好掌握里面的绕过细节,有助于我们更好的去发现XSS漏洞以及XSS的防御。本文更多的是分享解析的细节,不是一个标准的答案,希望大家在渗透的时候有更多的思维。…...
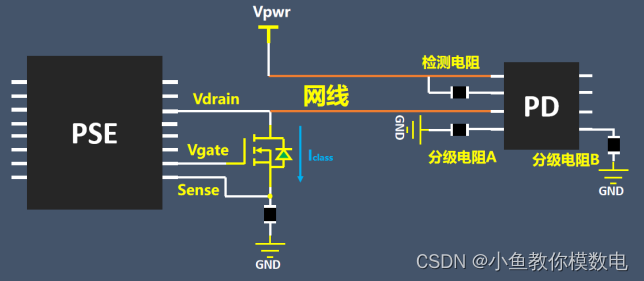
什么是以太网供电POE
POE指的是以太网供电,就是一根网线在传输网络的同时还传输设备所需的电源。我们最常见的就是通过POE交换机连接网络摄像头,网络摄像头无需的电源适配器,仅靠一根网线就能实现电源和网络的传输。POE供电一般可以到100米。POE包含两个部分&…...
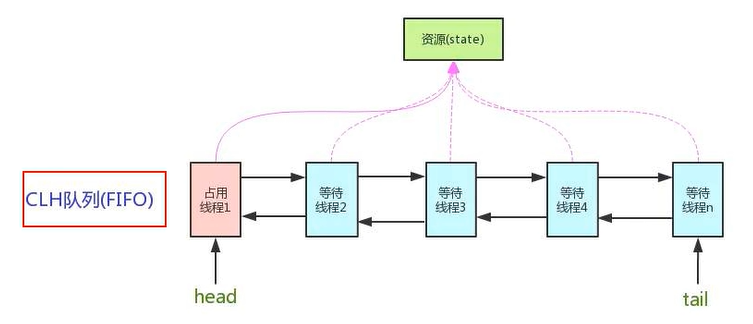
【JUC2022】第七章 AQS、ReentrantReadWriteLock 和 StampedLock
【JUC2022】第七章 AQS 文章目录【JUC2022】第七章 AQS一、AQS1.概述2.同步器3.抽象的4.队列式二、ReentrantReadWriteLock1.概述2.案例3.存在的问题三、StampedLock1.概述2.案例3.存在的问题一、AQS 1.概述 AQS(AbstractQueueSynchronizer,抽象的队列式同步器)&am…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
