链式二叉树--前序中序后序遍历,高度,节点个数问题
目录
前言:
一:链式二叉树的结构定义
二:链式二叉树的遍历--->前序,中序,后序
1.前序
递归展开图分析
2.中序
递归展开图分析
3.后序
三:二叉树结点的求解
1.二叉树总结点
递归展开分析
2.二叉树叶子结点数
递归展开分析
3.二叉树第k层节点个数
递归展开分析
四:二叉树的高度
五:总结语

接下来的日子会顺顺利利,万事胜意,生活明朗-----------林辞忧
前言:
链式二叉树作为后续AVL树,B系列树的雏形,理解掌握链式二叉树的各种操作很重要,此处就需要用递归来实现链式二叉树的各种操作,相信认真学习过后会对递归有更深刻的理解,接下来我们就开始上菜
一:链式二叉树的结构定义
链式二叉树的结构由指针域和数值域组成,况且链式二叉树并不都是完全二叉树,还有普通二叉树,每个节点最多两个孩子
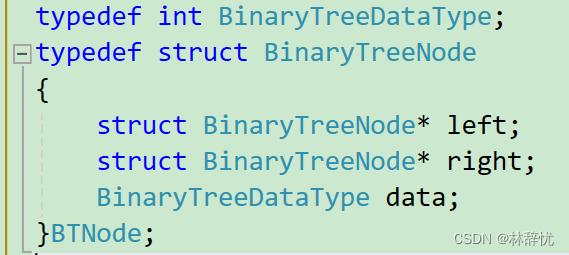
二:链式二叉树的遍历--->前序,中序,后序
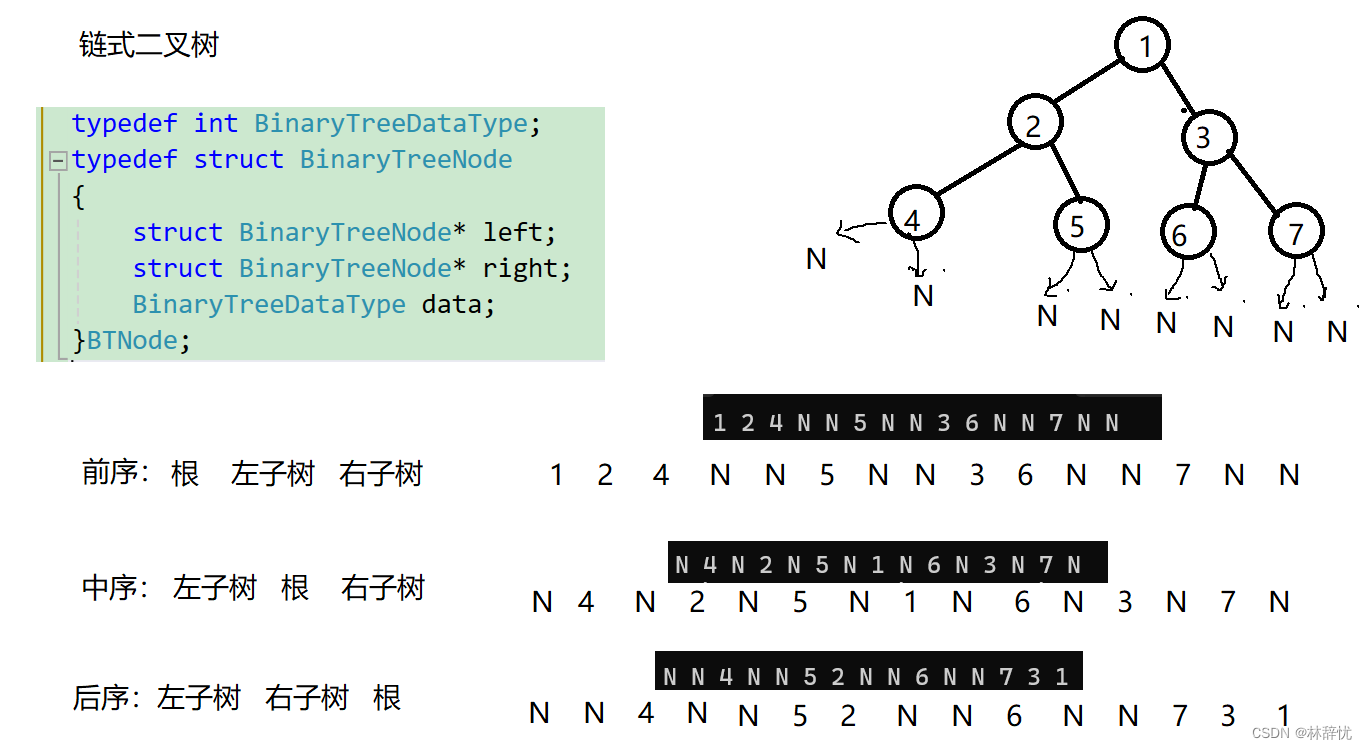
1.前序
BTNode* Buynode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail\n");return NULL;}newnode->left = NULL;newnode->right = NULL;newnode->data = x;return newnode;
}BTNode* CreatTree()
{BTNode* n1 = Buynode(1);BTNode* n2 = Buynode(2);BTNode* n3 = Buynode(3);BTNode* n4 = Buynode(4);BTNode* n5 = Buynode(5);BTNode* n6 = Buynode(6);BTNode* n7 = Buynode(7);n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;return n1;
}
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return ;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}递归展开图分析

2.中序
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}递归展开图分析

3.后序
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}后续递归展开图同上展开即行
三:二叉树结点的求解
1.二叉树总结点
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL)//递归结束条件{return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;//从左子树和右子树中分别计数
}
递归展开分析
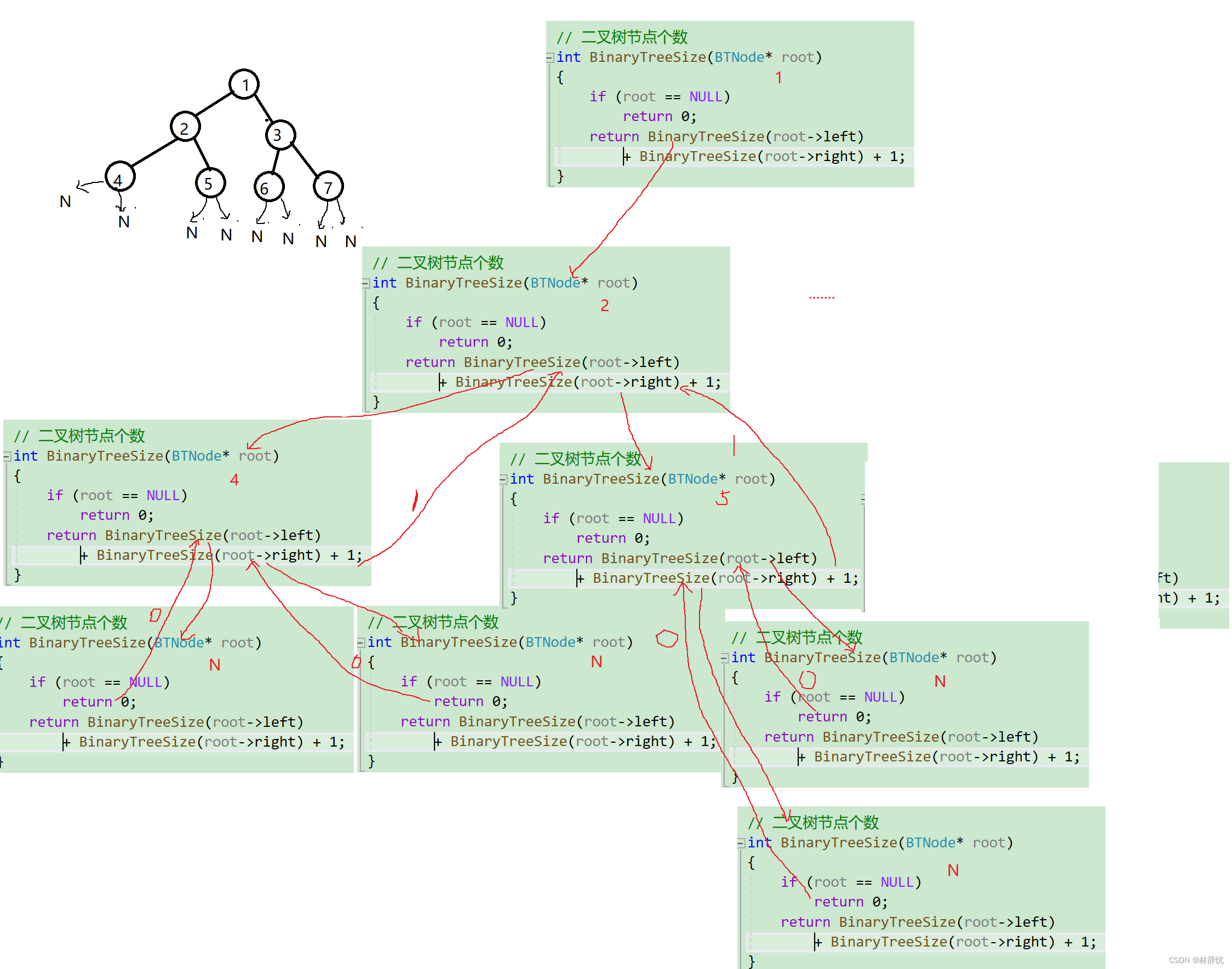
2.二叉树叶子结点数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)//空树返回0return 0;if (root->left == NULL && root->right == NULL)//叶子节点无孩子return 1;return BinaryTreeLeafSize(root->left)//递归往下寻找 + BinaryTreeLeafSize(root->right);
}递归展开分析

3.二叉树第k层节点个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)//循环走到k==1时停止,且不为空return 1;//分治思想:转化为求k-1层的节点数return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root, k - 1);
}递归展开分析
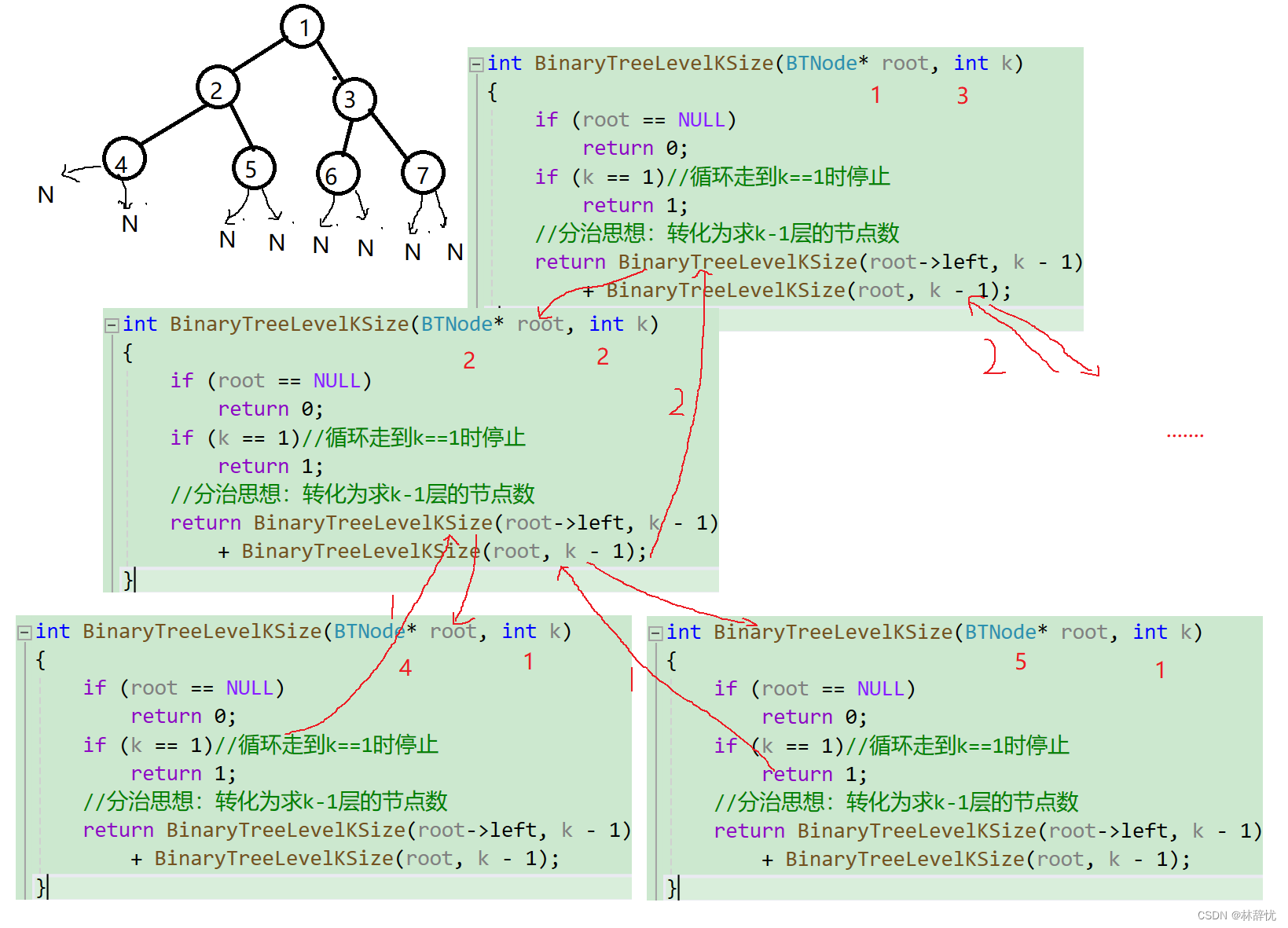
四:二叉树的高度
//二叉树的高度
int BinaryTreeHeight(BTNode* root)
{if (root == NULL)return 0;//记录左右长度,再进行比较int leftHeight = BinaryTreeHeight(root->left);int rightHeight = BinaryTreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}此图递归展开图就省略了昂
五:总结语
学会二叉树得学会画图,实在不懂时,画画递归展开图会好很多的
相关文章:

链式二叉树--前序中序后序遍历,高度,节点个数问题
目录 前言: 一:链式二叉树的结构定义 二:链式二叉树的遍历--->前序,中序,后序 1.前序 递归展开图分析 2.中序 递归展开图分析 3.后序 三:二叉树结点的求解 1.二叉树总结点 递归展开分析 2…...
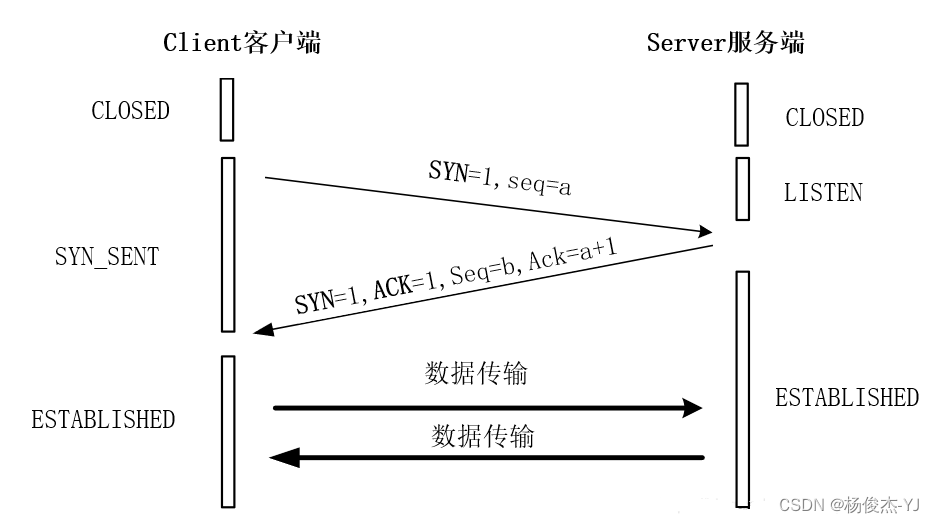
HCIA——TCP协议详解
目录 1、TCP概念及协议头部格式 1.1TCP特点 1.2TCP协议协议头部格式 1.3字段进行介绍 1.3.1源端口和目的端口 1.3.2序号(seq) 1.3.3确认序号(ack) 1.3.4数据偏移 1.3.5标志位 1.3.6窗口 1.3.7校验和 1.3.8紧急指针 2、TCP的可靠性 2.1 TCP可靠性的保障 2.2排序机…...

Hadoop大数据应用:Linux 部署 HDFS 分布式集群
目录 一、实验 1.环境 2.Linux 部署 HDFS 分布式集群 3.Linux 使用 HDFS 文件系统 二、问题 1.ssh-copy-id 报错 2. 如何禁用ssh key 检测 3.HDFS有哪些配置文件 4.hadoop查看版本报错 5.启动集群报错 6.hadoop 的启动和停止命令 7.上传文件报错 8.HDFS 使用命令 一…...

纯 CSS 实现文字换行环绕效果
实现效果 实现代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>Document</title><…...
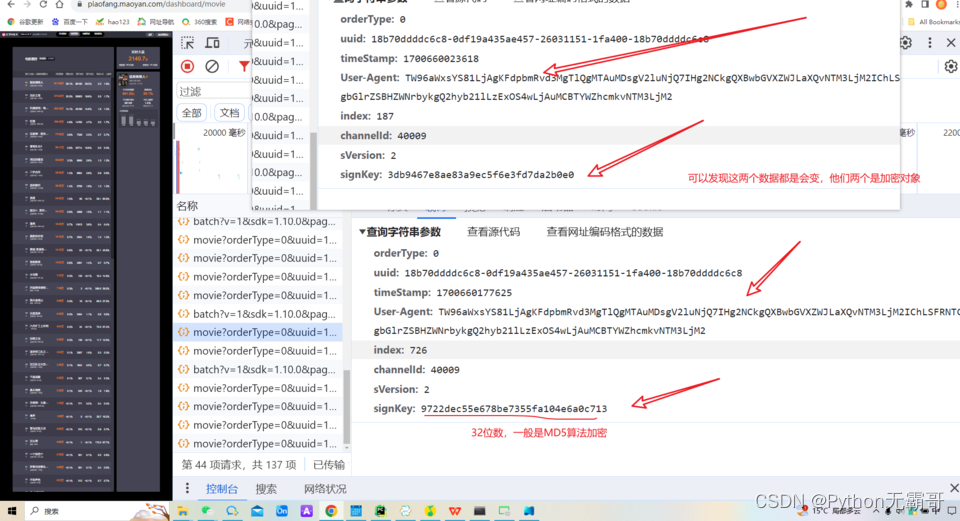
【爬虫逆向】Python逆向采集猫眼电影票房数据
进行数据抓包,因为这个网站有数据加密 !pip install jsonpathCollecting jsonpathDownloading jsonpath-0.82.2.tar.gz (10 kB)Preparing metadata (setup.py) ... done Building wheels for collected packages: jsonpathBuilding wheel for jsonpath (setup.py) .…...

解析服务器下载速度:上行、下行与带宽之谜
在日常使用中,我们经常会遇到从服务器下载内容速度忽快忽慢的情况,即便服务器的硬件配置如4核CPU、8GB内存和12Mbps的带宽看似足够。为何会出现这种现象?这背后涉及到网络中的上行、下行以及带宽等关键概念。本文旨在揭开这些术语背后的含义&…...

计算机网络的概念
目录 <计算机网络的定义> <计算机网络的形成与发展> 1.第一阶段远程联机阶段----60年代以前: 2.第二阶段多机互联网络阶段----60年代中期: 3.第三阶段标准化网络阶段----70年代末: 4.第四阶段网络互联与高速网络阶段一90年代: <计算机网络的未来--下一代…...

MATLAB中的脚本和函数有什么区别?
MATLAB中的脚本和函数是两种不同的代码组织方式,它们在结构、功能和使用方式上有显著的区别。以下是对这两种方式的详细解释,总计约2000字。 一、MATLAB脚本 MATLAB脚本是一种包含多条MATLAB命令的文件,这些命令按照在文件中的顺序依次执行…...

从电影《沙丘》说起——对人工智能的思考
正文 从《沙丘》开始说起 之前看《沙丘》电影,里面有一类角色叫门泰特,这类人大脑可以飞快地运算,在电影设定里是替换人工智能、机器运算的存在。男主保罗也是这类型的人,但他可能基因更强大,吸食了香料后࿰…...

使用Python进行自然语言处理(NLP):NLTK与Spacy的比较【第133篇—NLTK与Spacy】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 使用Python进行自然语言处理(NLP):NLTK与Spacy的比较 自…...
)
学习笔记--在线强化学习与离线强化学习的异同(3)
这篇博文很多部分仅代表个人学习观点,欢迎大家与我一起讨论 强化学习与离线强化学习的区别 强化学习和离线强化学习都是机器学习的分支,主要用于训练智能体以在不断尝试和错误的过程中学习如何最大化累积奖励。它们之间的主要区别在于数据的获取方式和训…...

使用Thymeleaf导出PDF,页眉插入图片与内容重叠?
CSS 打印分页功能 需求:打印 在第一页的内容被挤到第二页的时候,又想每一页页头都有相同的样式,使用页眉。 问题:第二页的内容与页眉重叠了? 查各路找出的原因:header 页眉不占空间 解决:不…...

python网络编程:通过socket实现TCP客户端和服务端
目录 写在开头 socket服务端(基础) socket客户端(基础) 服务端实现(可连接多个客户端) 客户端实现 数据收发效果 写在开头 近期可能会用python实现一些网络安全工具,涉及到许多关于网络…...

论文阅读——RSGPT
RSGPT: A Remote Sensing Vision Language Model and Benchmark 贡献:构建了一个高质量的遥感图像描述数据集(RSICap)和一个名为RSIEval的基准评估数据集,并在新创建的RSICap数据集上开发了基于微调InstructBLIP的遥感生成预训练…...

长连接技术
个人学习记录,欢迎指正 1.轮询 1.1 轮询的形式 短连接轮询 前端每隔一段时间向服务端发起一次Http请求来获取数据。 const shortPolling () > { const intervalHandler setInterval(() > {fetch(/xxx/yyy).then(response > response.json()).then(respo…...

供电系统分类详解
一、供电系统分类 电力供电系统一般有5种供电模式,常用的有:IT系统,TT系统,TN系统,其中TN系统又可以分为TN-C,TN-S,TN-C-S。 1、TN-C系统(三相四线制) 优点: 该系统中…...
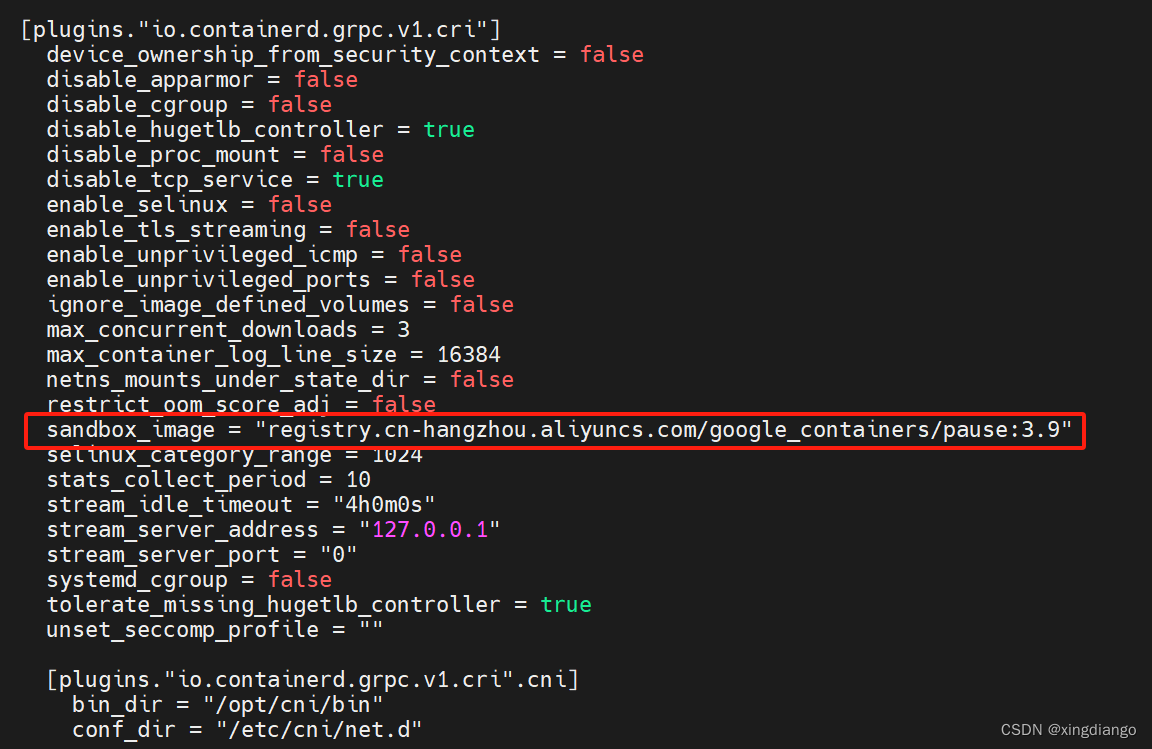
基于centos7的k8s最新版v1.29.2安装教程
k8s概述 Kubernetes 是一个可移植、可扩展的开源平台,用于管理容器化的工作负载和服务,可促进声明式配置和自动化。 Kubernetes 拥有一个庞大且快速增长的生态,其服务、支持和工具的使用范围相当广泛。 Kubernetes 这个名字源于希腊语&…...

【赠书第20期】AI绘画与修图实战:Photoshop+Firefly从入门到精通
文章目录 前言 1 入门篇:初识Photoshop与Firefly 2 进阶篇:掌握Photoshop与Firefly的核心技巧 3 实战篇:运用Photoshop与Firefly进行创作 4 精通篇:提升创作水平,拓展应用领域 5 结语 6 推荐图书 7 粉丝福利 前…...

如何在并行超算云上玩转PWmat③:使用Q-Flow提交计算的案例演示
3月的每周二下午14:00我们将会在并行直播间为大家持续带来线上讲座。前面两期我们分享了”PWmat特色功能和应用“以及“如何在并行超算云平台使用PWmat计算软件”主题讲座,回看视频和PPT已上传至B站”龙讯旷腾“账号内。 本周张持讲师将继续带着大家手把手上机教学…...

html5cssjs代码 017样式示例
html5&css&js代码 017样式示例 一、代码二、解释 这段HTML代码定义了一个网页的基本结构,包括头部、主体和尾部。在头部中,设置了网页标题、字符编码和样式。主体部分包含一个标题和一个表格,表格内分为两个单元格,左侧为…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
