2024/3/14打卡棋子(14届蓝桥杯)——差分
标准差分模板 差分——前缀和的逆运算(一维+二维)-CSDN博客
题目
小蓝拥有 n×n 大小的棋盘,一开始棋盘上全都是白子。
小蓝进行了 m 次操作,每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色,黑色棋子变为白色)。
请输出所有操作做完后棋盘上每个棋子的颜色。
输入格式
输入的第一行包含两个整数 n,m,用一个空格分隔,表示棋盘大小与操作数。
接下来 m 行每行包含四个整数 x1,y1,x2,y2,相邻整数之间使用一个空格分隔,表示将在 x1 至 x2 行和 y1 至 y2 列中的棋子颜色取反。
输出格式
输出 n 行,每行 n 个 0 或 1 表示该位置棋子的颜色。
如果是白色则输出 0,否则输出 1。
数据范围
对于 30% 的评测用例,1≤n,m≤500;
对于所有评测用例,1≤n,m≤2000,1≤x1≤x2≤n,1≤y1≤y2≤n。输入样例:
3 3 1 1 2 2 2 2 3 3 1 1 3 3输出样例:
001 010 100
方法
针对于改变一个区间的值进行改变,(无论是加,减等),都可以考虑使用差分来做。
差分定义:给定一个原数组,构造一个差分数组
, 使得
。
因此,这里可以选用二维差分:
差分——前缀和的逆运算(一维+二维)-CSDN博客 (对差分的详解)
对于该题来说,可以发现,翻奇数次是黑子,翻偶数次是白子。因此如果我们想要改变某个区间的值 ,我们可以直接选择对于该区间的每个数+1,如果最终结果是偶数,就用0表示,奇数用1表示。
代码
import java.io.*;
// 直接+1,如果是偶数,则为白子,否则为黑子
class Main{static int N = 2010;static int n,m;static int[][] a = new int[N][N];public static void main(String[] args) throws IOException{BufferedReader in = new BufferedReader(new InputStreamReader(System.in));BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));String[] s = in.readLine().split(" ");n = Integer.parseInt(s[0]);m = Integer.parseInt(s[1]);while(m-->0){s = in.readLine().split(" ");int x1 = Integer.parseInt(s[0]);int y1 = Integer.parseInt(s[1]);int x2 = Integer.parseInt(s[2]);int y2 = Integer.parseInt(s[3]);insert(x1,y1,x2,y2); // 对每个区间进行差分}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){a[i][j] = a[i-1][j]+a[i][j-1]-a[i-1][j-1]+a[i][j]; // 计算前缀和,即a[i][j]if(a[i][j]%2==0) out.write("0");else out.write("1");}out.write("\n");}out.close();}// 差分计算public static void insert(int x1,int y1,int x2,int y2){a[x1][y1] += 1;a[x1][y2+1] -= 1;a[x2+1][y1] -= 1;a[x2+1][y2+1] += 1;}
}相关文章:
2024/3/14打卡棋子(14届蓝桥杯)——差分
标准差分模板 差分——前缀和的逆运算(一维二维)-CSDN博客 题目 小蓝拥有 nn 大小的棋盘,一开始棋盘上全都是白子。 小蓝进行了 m 次操作,每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色࿰…...
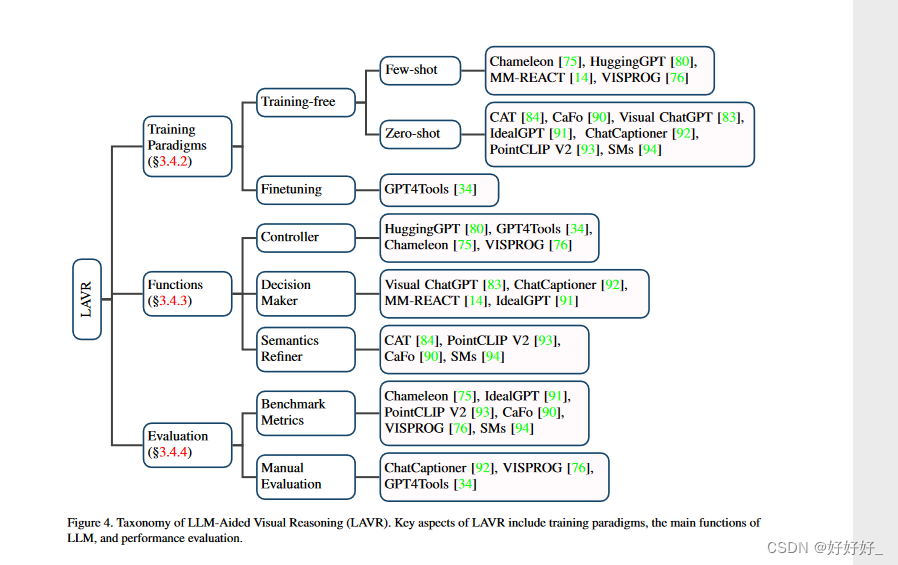
A Survey on Multimodal Large Language Models
目录 1. Introduction2. 概述方法多模态指令调优 3.1.1 简介3.1.2 预备知识3.1.3 模态对齐3.1.4 数据3.1.5 模态桥接3.1.6 评估 3.2.多模态情境学习3.3.多模态思维链3.3.1 模态桥接3.3.2 学习范式3.3.3 链配置3.3.4 生成模式3.4.LLMs辅助视觉推理3.4.1 简介3.4.2 训练范式3.4.3…...
一)
Java面向对象编程(高级)一
在Java中,面向对象编程更是核心设计理念之一,为开发者提供了丰富的工具和特性来创建灵活、可扩展的应用程序。 本博客将深入探讨Java面向对象编程的高级特性,包括但不限于多态、继承、封装、抽象类、接口等方面的内容。我们将从实际案例出发…...

1056:点和正方形的关系
【题目描述】 有一个正方形,四个角的坐标(x,y)分别是(1,-1),(1,1),(-1,-1),(-1,1),x是横轴,y是纵轴。写一个程序,判断一个给定的点是…...
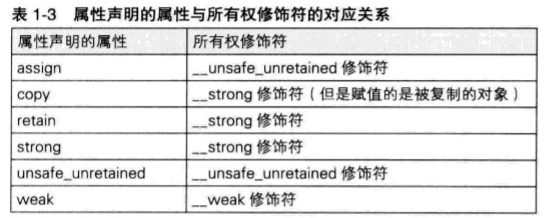
【iOS】ARC学习
文章目录 前言一、autorelease实现二、苹果的实现三、内存管理的思考方式__strong修饰符取得非自己生成并持有的对象__strong 修饰符的变量之间可以相互赋值类的成员变量也可以使用strong修饰 __weak修饰符循环引用 __unsafe_unretained修饰符什么时候使用__unsafe_unretained …...
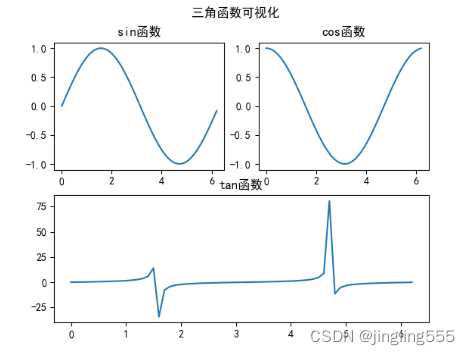
数据分析 | Matplotlib
Matplotlib 是 Python 中常用的 2D 绘图库,它能轻松地将数据进行可视化,作出精美的图表。 绘制折线图: import matplotlib.pyplot as plt #时间 x[周一,周二,周三,周四,周五,周六,周日] #能量值 y[61,72,66,79,80,88,85] # 用来设置字体样式…...

mac npm install 很慢或报错
npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/pnpm failed, reason: certificate has expired 1、取消ssl验证: npm config set strict-ssl false 修改后一般就可以了,…...

100天精通Python(实用脚本篇)——第118天:基于selenium和ddddocr库实现反反爬策略之验证码识别
文章目录 专栏导读一、前言二、ddddocr库使用说明1. 介绍2. 算法步骤3. 安装4. 参数说明5. 纯数字验证码识别6. 纯英文验证码识别7. 英文数字验证码识别8. 带干扰的验证码识别 三、验证码识别登录代码实战1. 输入账号密码2. 下载验证码3. 识别验证码并登录 书籍推荐 专栏导读 …...

51单片机与ARM单片机的区别
51的MCU与ARM的MCU的区别 51单片机与ARM单片机区别主要体现在以下几个方面: 指令集架构(ISA): 51单片机:基于Intel 8051架构,采用的是CISC(复杂指令集计算机)设计,其指令…...

Android 10.0 mtk平台系统添加公共so库的配置方法
1.前言 在10.0的系统定制化开发中,由于 Android对应用应用的系统库限制越来越严格,上层应用包括(apk、jar包)不能直接引用系统的一些so库了。如果需要使用,只能使用,系统申明的公共库。 如果使用非系统申明的公共库,apk运行后调用该so库时,app会直接挂掉,或者系统开发…...
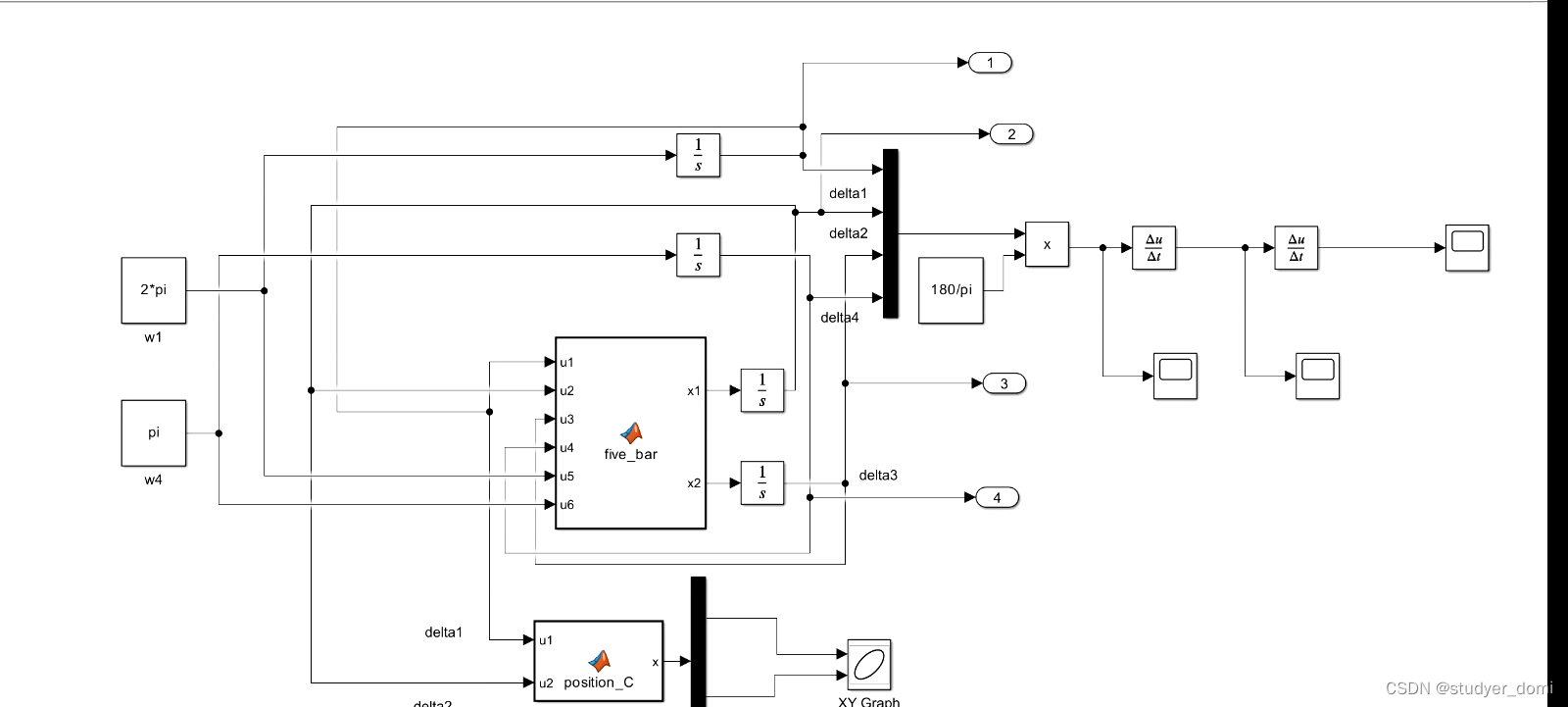
simulink平面五杆机构运动学仿真
1、内容简介 略 68-可以交流、咨询、答疑 2、内容说明 simulink平面五杆机构运动学仿真 [ 摘 要 ] 以 MATLAB 程序设计语言为平台 , 以平面可调五杆机构为主要研究对象 , 给定机构的尺寸参数 , 列出所 要分析机构的闭环矢量方程 , 使用 MATLAB 软件中 SIMULINK 仿真工…...

【Docker】APISIX Ingress Controller部署
APISIX Ingress Controller环境标准软件基于Bitnami apisix-ingress-controller:构建。当前版本为1.8.0 你可以通过轻云UC部署工具直接安装部署,也可以手动按如下文档操作,该项目已经全面开源,可以从如下环境获取 配置文件地址: https://git…...

常见的十大网络安全攻击类型
常见的十大网络安全攻击类型 网络攻击是一种针对我们日常使用的计算机或信息系统的行为,其目的是篡改、破坏我们的数据,甚至直接窃取,或者利用我们的网络进行不法行为。你可能已经注意到,随着我们生活中越来越多的业务进行数字化&…...

接口幂等性问题和常见解决方案
接口幂等性问题和常见解决方案 1.什么是接口幂等性问题1.1 会产生接口幂等性的问题1.2 解决思路 2.接口幂等性的解决方案2.1 唯一索引解决方案2.2 乐观锁解决方案2.3 分布式锁解决方案2.4 Token解决方案(最优方案) 3 Token解决方案落地3.1 token获取、token校验3.2 自定义注解,…...
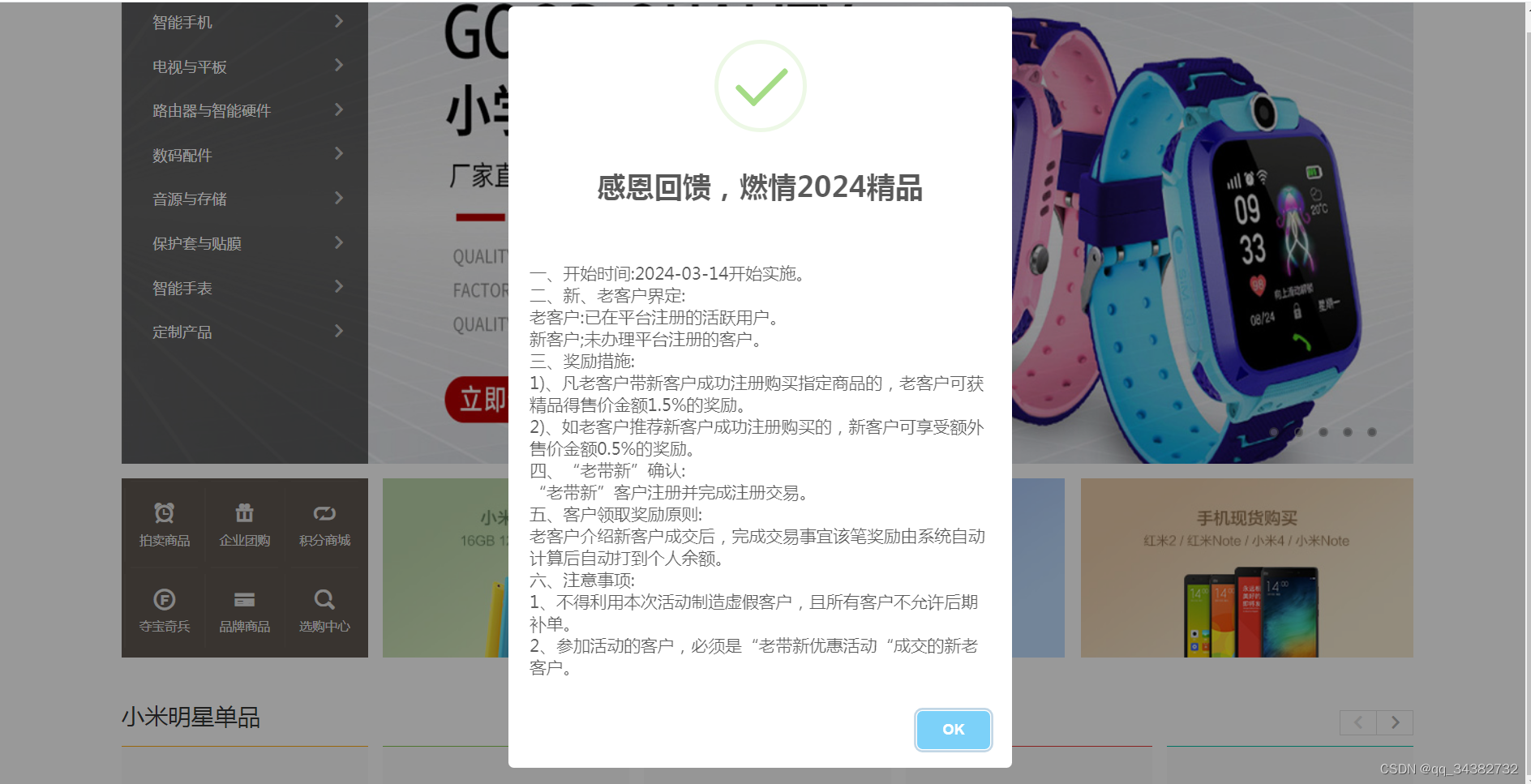
网站首页添加JS弹屏公告窗口教程
很多小白站长会遇到想给自己的网站添加一个弹屏公告,用于做活动说明、演示站提示等作用与目的。 下面直接上代码:(直接复制到网页头部、底部php、HTML文件中) <script src"https://www.mohuda.com/site/js/sweetalert.m…...

【Rockchip 安10.1 默认给第三方apk默认开启所有权限】
Rockchip 安10.1 默认给第三方apk默认开启所有权限 问题描述解决方法 郑重声明:本人原创博文,都是实战,均经过实际项目验证出货的 转载请标明出处:攻城狮2015 Platform: Rockchip 3229 OS:Android 10.1 Kernel: 4.19 问题描述 有些第三方或者主界面&…...
python-redis缓存装饰器
目录 redis_decorator安装查看源代码使用 redis_decorators安装查看源代码\_\_init\_\_.pycacheable.py 各种可缓存的类型cache_element.py 缓存的元素caching.py 缓存主要逻辑 使用 总结全部代码参考 redis_decorator 安装 pip install redis_decorator查看源代码 from io …...

每个私域运营者都必须掌握的 5 大关键流量运营核心打法!
很多人觉得私域运营比较简单,只是运营的事情,但事实并非如此,私域运营体系非常大,包含了公私域联动、品牌运营、品类战略,它是一个自上而下,由内到外的系统化工程。 很多人天天在想着如何引流拓客…...

蓝桥杯--平均
在编程竞赛,尤其是参与蓝桥杯的过程中,遇到各种问题需求是家常便饭。最近,我遇到了一个非常有趣且颇具挑战性的算法问题。问题描述如下:对于一个长度为n的数组(n是10的倍数),数组中的每个元素均…...
未来已来:科技驱动的教育变革
我们的基础教育数百年来一成不变。学生们齐聚在一个物理空间,听老师现场授课。每节课时长和节奏几乎一致,严格按照课表进行。老师就像“讲台上的圣人”。这种模式千篇一律,并不适用于所有人。学生遇到不懂的问题,只能自己摸索或者…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
