2024蓝桥杯每日一题(DFS)
备战2024年蓝桥杯 -- 每日一题
Python大学A组
试题一:奶牛选美
试题二:树的重心
试题三:大臣的差旅费
试题四:扫雷
试题一:奶牛选美
【题目描述】
听说最近两斑点的奶牛最受欢迎,约翰立即购进了一批两斑点牛。不幸的是,时尚潮流往往变化很快,当前最受欢迎的牛变成了一斑点牛。约翰希望通过给每头奶牛涂色,使得它们身上的两个斑点能够合为一个斑点,让它们能够更加时尚。牛皮可用一个 N×M的字符矩阵来表示,如下所示:
................
..XXXX....XXX...
...XXXX....XX...
.XXXX......XXX..
........XXXXX...
.........XXX....其中,X表示斑点部分。如果两个 X在垂直或水平方向上相邻(对角相邻不算在内),则它们属于同一个斑点,由此看出上图中恰好有两个斑点。约翰牛群里所有的牛都有两个斑点。约翰希望通过使用油漆给奶牛尽可能少的区域内涂色,将两个斑点合为一个。在上面的例子中,他只需要给三个 .. 区域内涂色即可(新涂色区域用 ∗ 表示):
................
..XXXX....XXX...
...XXXX*...XX...
.XXXX..**..XXX..
........XXXXX...
.........XXX....请帮助约翰确定,为了使两个斑点合为一个,他需要涂色区域的最少数量。
【输入格式】
第一行包含两个整数 N和 M。
接下来 N 行,每行包含一个长度为 M 的由 X 和 .. 构成的字符串,用来表示描述牛皮图案的字符矩阵。
【输出格式】
输出需要涂色区域的最少数量。
【数据范围】
1≤N,M≤50
【输入样例】
6 16
................
..XXXX....XXX...
...XXXX....XX...
.XXXX......XXX..
........XXXXX...
.........XXX....【输出样例】
3【解题思路】
用2次BFS,第一次用来找出两个斑点,第二次用来找最短的连接线。
【Python程序代码】
from collections import *
n,m = map(int,input().split())
a = []
for i in range(n):a.append(list(input()))
st = [[0]*(m+5) for _ in range(n+5) ]
t,f = 1,0
for i in range(n):for j in range(m):if a[i][j]=='X' and st[i][j]==0:q=deque()q.append([i,j])st[i][j]=twhile q:tx,ty = q.popleft()for zx,zy in [(-1,0),(1,0),(0,-1),(0,1)]:nx,ny = tx+zx,ty+zyif nx<0 or nx>=n or ny<0 or ny>=m:continueif a[nx][ny]=='.' or st[nx][ny]:continuest[nx][ny]=tq.append([nx,ny])t += 1def bfs(i_,j_):q = deque()q.append([i_,j_,0])vis = [[0]*(m+5) for _ in range(n+5) ]vis[i_][j_]=1while q:tx,ty,z = q.popleft()if st[tx][ty]==2:return zfor zx,zy in [(-1,0),(1,0),(0,1),(0,-1)]:nx,ny = tx+zx,ty+zyif nx < 0 or nx >= n or ny < 0 or ny >= m: continueif vis[nx][ny]: continuevis[nx][ny]=1q.append([nx,ny,z+1])return 0res = n*m
for i in range(n):for j in range(m):if st[i][j]==1:tep = bfs(i,j)res = min(res,tep)
print(res-1)试题二:树的重心
【题目描述】
给定一颗树,树中包含 n个结点(编号 1∼n)和 n−1 条无向边。请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
【输入格式】
第一行包含整数 n,表示树的结点数。
接下来 n−1行,每行包含两个整数 a 和 b,表示点 a 和点 b 之间存在一条边。
【输出格式】
输出一个整数 m,表示将重心删除后,剩余各个连通块中点数的最大值。
【数据范围】
1≤n≤100000
【输入样例】
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6【输出样例】
4【解题思路】
本体上就是一个树的遍历问题,遍历去掉每一个点,找出答案。
【Python程序代码】
n = int(input())
h,e,ne,idx = [-1]*(n+5),[0]*(2*n+5),[0]*(2*n+5),0
def add(a,b):global idxe[idx]=b; ne[idx]=h[a]; h[a]=idx; idx+=1
for i in range(n-1):a,b = map(int,input().split())add(a,b); add(b,a)
ans,st = n,[False]*(n+5)
def dfs(u):global ansst[u]=Trueres,sumv = 0,1i = h[u]while i!=-1:j = e[i]if not st[j]:s = dfs(j)res = max(res,s)sumv += si = ne[i]res = max(res,n-sumv)ans = min(ans,res)return sumv
dfs(1)
print(ans)
试题三: 大臣的旅费
【题目描述】
很久以前,T王国空前繁荣。为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。为节省经费,T 国的大臣们经过思考,制定了一套优秀的修建方案,使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。J 是 T 国重要大臣,他巡查于各大城市之间,体察民情。所以,从一个城市马不停蹄地到另一个城市成了 J最常做的事情。他有一个钱袋,用于存放往来城市间的路费。聪明的 J发现,如果不在某个城市停下来修整,在连续行进过程中,他所花的路费与他已走过的距离有关。具体来说,一段连续的旅途里,第 1千米的花费为 11,第 2 千米的花费为 12,第 3 千米的花费为 13,…,第 x 千米的花费为 x+10。也就是说,如果一段旅途的总长度为 1 千米,则刚好需要花费 11,如果一段旅途的总长度为 2 千米,则第 1千米花费 11,第 2 千米花费 12,一共需要花费 11+12=23。J 大臣想知道:他从某一个城市出发,中间不休息,到达另一个城市,所有可能花费的路费中最多是多少呢?
【输入样例】

【输出格式】
输出一个整数,表示大臣 J 最多花费的路费是多少。
【数据范围】

【输入样例】
5
1 2 2
1 3 1
2 4 5
2 5 4【输出样例】
135【解题思路】
可以发现本题就是求树的直径的问题,经典做法就是先遍历找出距离点d最远的点x,然后找到距离x点最优的y点,其中x到y的距离就是树的直径。
【Python程序代码】
n = int(input())
mp = [[]for i in range(n+1)]
for i in range(n-1):a,b,c = map(int,input().split())mp[a].append([b,c])mp[b].append([a,c])
dist = [0]*(n+1)
def dfs(st,father,distance):dist[st] = distancefor b,c in mp[st]:if b!=father:dfs(b,st,distance+c)
dfs(1,-1,0)
u = 1
for i in range(1,n+1):if dist[i]>dist[u]:u=i
dfs(u,-1,0)
for i in range(1,n+1):if dist[i]>dist[u]:u=i
s = dist[u]
print( s*10 + s*(1+s)//2 ) 试题四:扫雷
【题目描述】
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下:在一个二维平面上放置着 n 个炸雷,第 i个炸雷 (xi,yi,ri)表示在坐标 (xi,yi)(处存在一个炸雷,它的爆炸范围是以半径为 ri 的一个圆。为了顺利通过这片土地,需要玩家进行排雷。玩家可以发射 m 个排雷火箭,小明已经规划好了每个排雷火箭的发射方向,第 j 个排雷火箭 (xj,yj,rj)表示这个排雷火箭将会在 (xj,yj)处爆炸,它的爆炸范围是以半径为 rj 的一个圆,在其爆炸范围内的炸雷会被引爆。同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
【输入格式】
输入的第一行包含两个整数 n、m。
接下来的 n 行,每行三个整数 xi,yi,ri表示一个炸雷的信息。
再接下来的 m 行,每行三个整数 xj,yj,rj表示一个排雷火箭的信息。
【输出格式】
输出一个整数表示答案。
【数据范围】 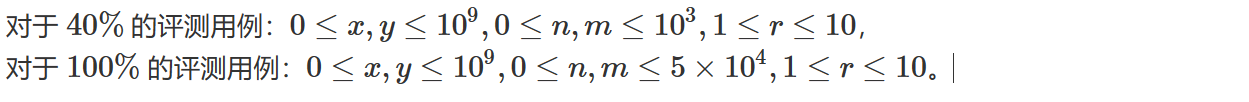
【输入样例】
2 1
2 2 4
4 4 2
0 0 5【输出样例】
2【解题思路】
首先,对在同一点的炸雷和排雷火箭进行去重处理,然后枚举每一个排雷火箭,遍历排雷范围,如果能扫到雷则该炸雷也存放到排雷火箭队列。最后用排雷火箭队列模拟排雷。
【Python程序代码】
import sys
from collections import *
input = sys.stdin.readline
n, m = map(int, input().split())
num = Counter()
find = dict()
for _ in range(n):x, y, r = map(int, input().split())if (x, y) not in find:find[(x, y)] = 0num[(x, y)] += 1find[(x, y)] = max(find[(x, y)], r)
pq = deque()
f = dict()
for _ in range(m):x, y, r = map(int, input().split())if (x, y) not in f:f[(x, y)] = 0f[(x, y)] = max(f[(x, y)], r)
for (x, y), r in f.items():for i in range(x - r, x + r + 1):for j in range(y - r, y + r + 1):if (i - x) ** 2 + (j - y) ** 2 <= r ** 2:if (i, j) in find:pq.append((i, j, find[(i, j)]))del find[(i, j)]
res = 0
while pq:x, y, r = pq.popleft()res += num[(x, y)]for i in range(x - r, x + r + 1, 1):for j in range(y - r, y + r + 1, 1):if (i - x) ** 2 + (j - y) ** 2 <= r ** 2:if (i, j) in find:pq.append((i, j, find[(i, j)]))del find[(i, j)]
print(res)相关文章:
2024蓝桥杯每日一题(DFS)
备战2024年蓝桥杯 -- 每日一题 Python大学A组 试题一:奶牛选美 试题二:树的重心 试题三:大臣的差旅费 试题四:扫雷 试题一:奶牛选美 【题目描述】 听说最近两斑点的奶牛最受欢迎,…...
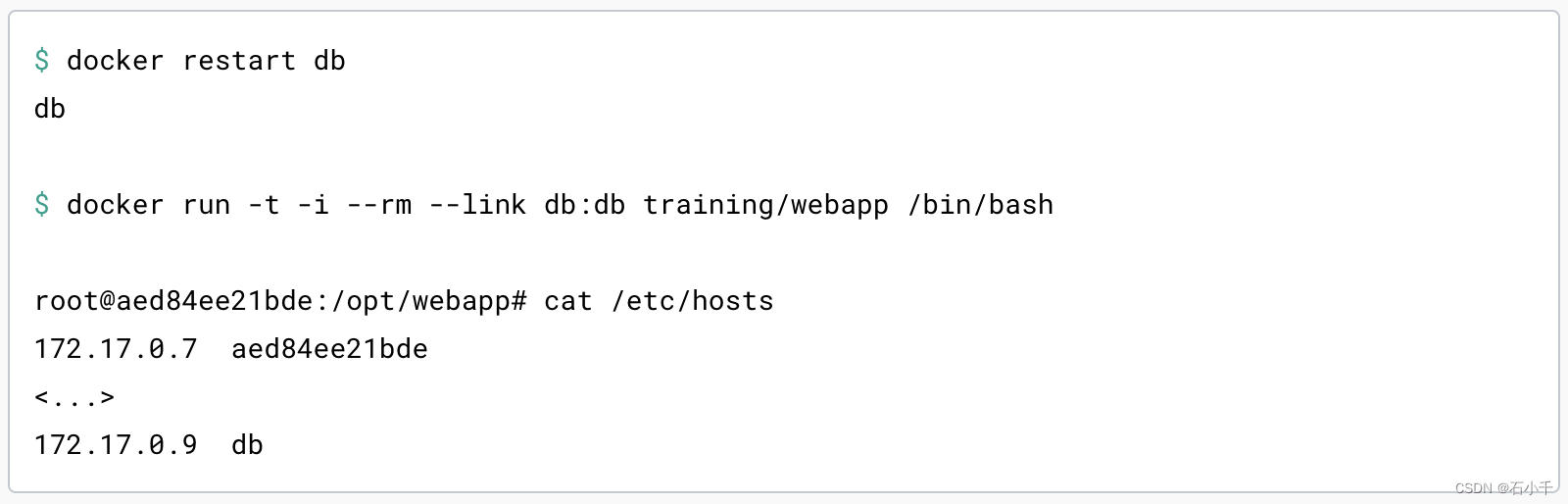
Docker 笔记(五)--链接
这篇笔记记录了Docker 的Link。 官方文档: Legacy container links - Communication across links 目录 参考Legacy container linksConnect using network port mappingConnect with the linking systemThe importance of naming Communication across linksEnviro…...
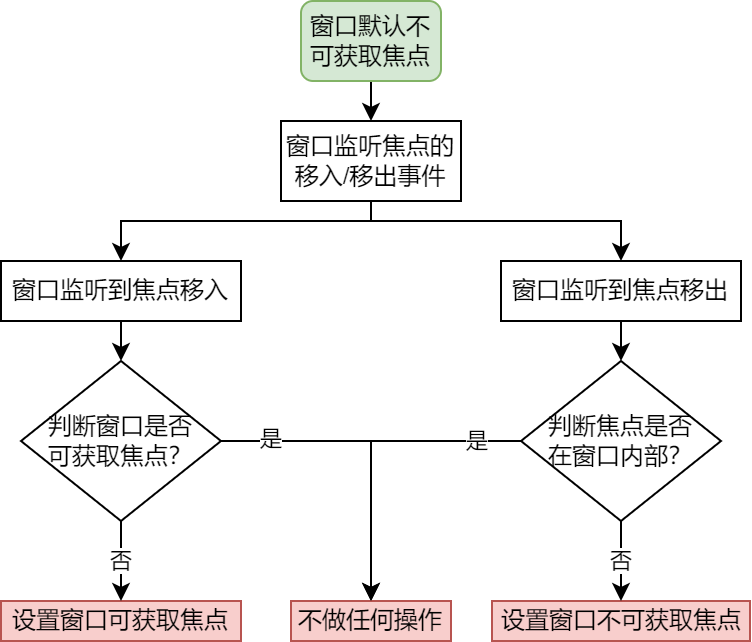
如何处理Android悬浮弹窗双击返回事件?
目录 1 前言 1.1 准备知识 1.2 问题概述 2 解决方案 3 代码部分 3.1 动态更新窗口焦点 3.2 窗口监听返回事件 3.3 判断焦点是否在窗口内部 3.4 窗口监听焦点移入/移出 4 注意事项 4.1 窗口范围 4.2 空隙处的返回事件处理 1 前言 1.1 准备知识 1)开发环…...

高可用篇_A Docker容器化技术_II Docker环境搭建和常见命令
原创作者:田超凡(程序员田宝宝) 版权所有,引用请注明原作者,严禁复制转载 Docker安装 Docker 要求 CentOS7 系统的内核版本在 3.10以上 ,查看本页面的前提条件来验证你的CentOS 版本是否支持 Docker 。 …...

Vue.js+SpringBoot开发食品生产管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 加工厂管理模块2.2 客户管理模块2.3 食品管理模块2.4 生产销售订单管理模块2.5 系统管理模块2.6 其他管理模块 三、系统展示四、核心代码4.1 查询食品4.2 查询加工厂4.3 新增生产订单4.4 新增销售订单4.5 查询客户 五、…...

Python面试笔记
Python面试笔记 PythonQ. Python中可变数据类型与不可变数据类型,浅拷贝与深拷贝详解Q. 解释什么是lambda函数?它有什么好处?Q. 什么是装饰器?Q. 什么是Python的垃圾回收机制?Q. Python内置函数dir的用法?Q…...

springboot 查看和修改内置 tomcat 版本
解析Spring Boot父级依赖 去到项目的根pom文件中,找到parent依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>${springboot.version}…...
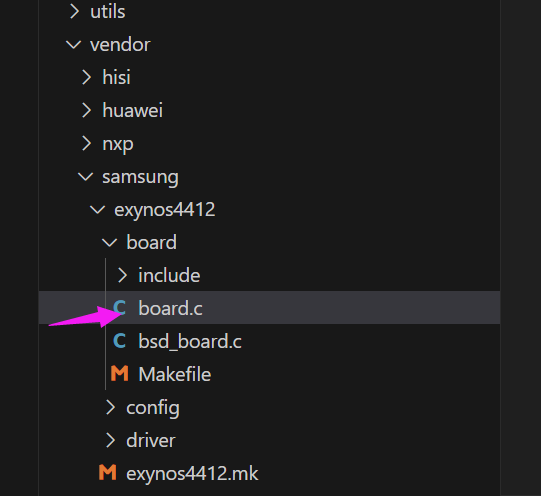
003——移植鸿蒙
目录 一、顶层Make分析 二、添加一个新的单板 2.1 Kconfig 2.2 Makefile 2.2.1 顶层Makefile 2.2.2 platform下的Makefile 2.2.3 platform下的bsp.mk文件 2.3 编译与调试 2.4 解决链接错误 三、内核启动流程的学习 3.1 韦东山老师总结的启动四步 3.2 启动文件分析…...

罗马数字转整数-力扣通过自己编译器编译
学会将力扣题目用自己自带的编译软件编译---纯自己想的本题解法 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例如, 罗马数字 2 写做 II ,即为两…...
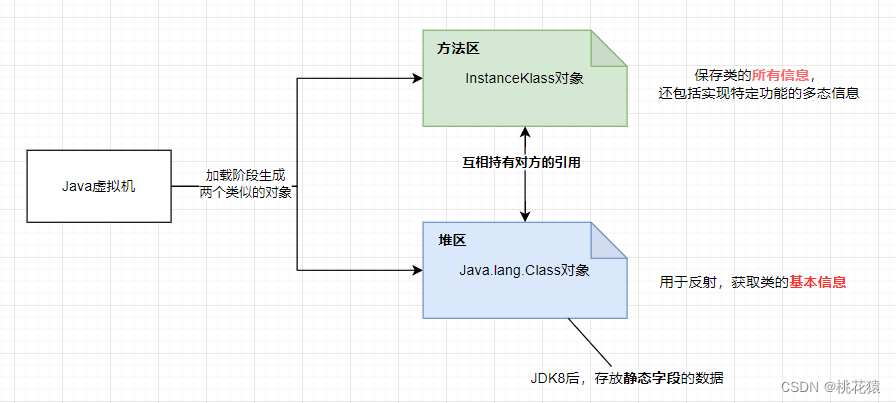
深入解析JVM加载机制
一、背景 Java代码被编译器变成生成Class字节码,但字节码仅是一个特殊的二进制文件,无法直接使用。因此,都需要放到JVM系统中执行,将Class字节码文件放入到JVM的过程,简称类加载。 二、整体流程 三、阶段逻辑分析 3…...
python redis中blpop和lpop的区别
python redis中lpop()方法是获取并删除左边第一个对象。 def lpop(self,name: str,count: Optional[int] None,) -> Union[Awaitable[Union[str, List, None]], Union[str, List, None]]:"""Removes and returns the first elements of the list name.By de…...

第四百一十回
文章目录 1. 概念介绍2. 方法与细节2.1 获取方法2.2 使用细节 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何获取当前系统语言"相关的内容,本章回中将介绍如何获取时间戳.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章…...
)
程序员的README——编写可维护的代码(一)
用户行为不可预测,网络不可靠,事情总会出错。生产环境下的软件必须一直保持可用状态。 编写可维护的代码有助于你应对不可预见的情况,可维护的代码有内置的保护、诊断和控制。 切记通过安全和有弹性的编码实践进行防御式编程来保护你的系统&a…...
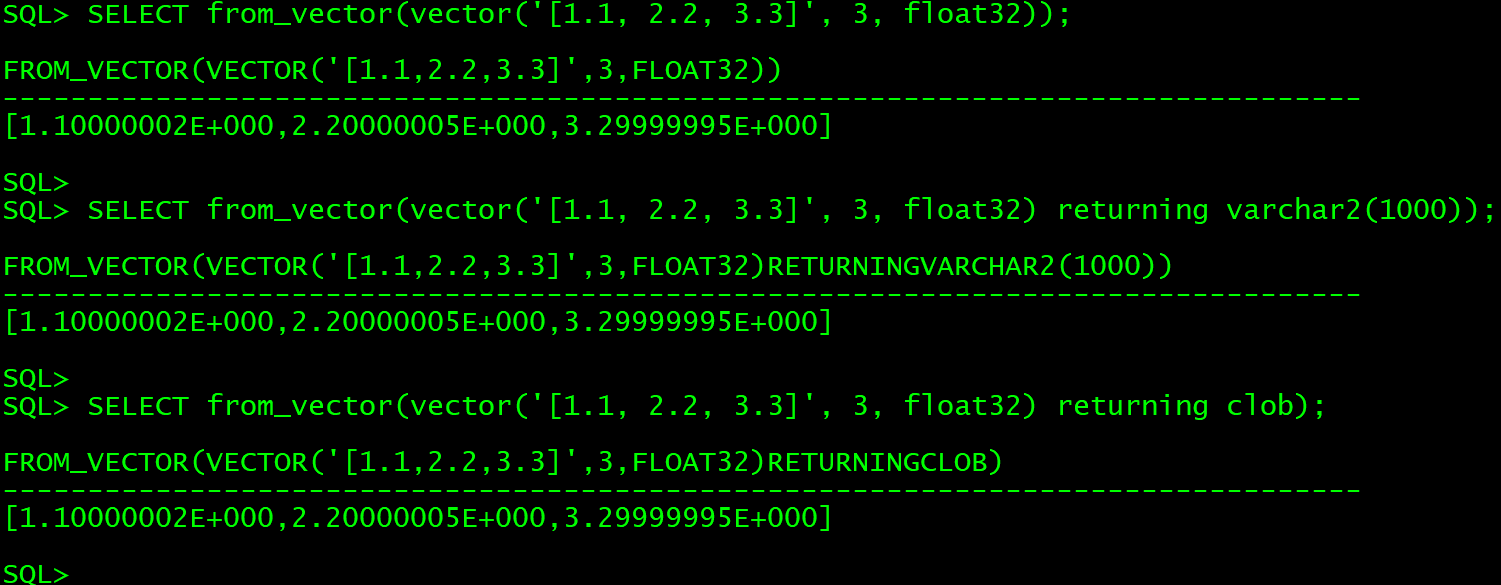
数据库管理-第160期 Oracle Vector DB AI-11(20240312)
数据库管理160期 2024-03-12 数据库管理-第160期 Oracle Vector DB & AI-11(20240312)1 向量的函数操作to_vector()将vector转换为标准值vector_norm()vector_dimension_count()vector_dimension_format() 2 将向量转换为字符串或CLOBvector_seriali…...
boost库笔记)
(C++进阶)boost库笔记
目录 1、boost::function 1.1 概述 1.2 boost包装器和C11包装器对比 1.2、代码示例 1、boost::function 1.1 概述 boost::function 是 Boost 库中提供的一个通用函数对象包装器,它可以存储指向任何可调用对象的指针,并且可以在任何时候通过 operat…...

MapReduce面试重点
文章目录 1. 简述MapReduce整个流程2. join原理 1. 简述MapReduce整个流程 数据划分(Input Splitting):开始时,输入数据被分割成逻辑上的小块,每个块被称为Input Split。 映射(Map):每个Input Split 由一个或多个Map任务处理&…...
从主函数中输入10个等长字符串,用一个函数对他们排序,然后在主函数输出这10个已排好序的字符串)
C语言简单题(7)从主函数中输入10个等长字符串,用一个函数对他们排序,然后在主函数输出这10个已排好序的字符串
从主函数中输入10个等长字符串,用一个函数对他们排序,然后在主函数输出这10个已排好序的字符串 /* 从主函数中输入10个等长字符串,用一个函数对他们排序,然后在主函数输出这10个已排好序的字符串 */ #include<stdio.h> …...

光伏科普|太阳能光伏发电应用场景有哪些?
太阳能光伏发电的应用领域其实非常广泛,很多人会不相信,但在我们的日常生活中随处可见太阳能光伏产业,本文将详细介绍其应用场景有哪些。 一、工业领域厂房 太阳能光伏发电作为一种清洁、可再生的能源,安装在工业领域厂房&#…...

Go 构建高效的二叉搜索树联系簿
引言 树是一种重要的数据结构,而二叉搜索树(BST)则是树的一种常见形式。在本文中,我们将学习如何构建一个高效的二叉搜索树联系簿,以便快速插入、搜索和删除联系人信息。 介绍二叉搜索树 二叉搜索树是一种有序的二叉…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的交通信号灯识别系统(深度学习+UI界面+训练数据集+Python代码)
摘要:本研究详细介绍了一种采用深度学习技术的交通信号灯识别系统,该系统集成了最新的YOLOv8算法,并与YOLOv7、YOLOv6、YOLOv5等早期算法进行了性能评估对比。该系统能够在各种媒介——包括图像、视频文件、实时视频流及批量文件中——准确地…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
