【FMCW 04】测角-Angle FFT
在之前的文章中,我们已经详尽讨论过FMCW雷达测距和测速的原理,现在来讲最后一块内容,测角。测角对于硬件设备具有要求,即要求雷达具有多发多收结构,从而形成多个空间信道(channel),我们正是利用这些channel间的差异性来完成对目标的测角。
本节讲述通用的Angle FFT测角的原理。
天线阵列
在一个具有多发多收的天线结构中,我们可以得到一个天线阵列(array)。一个Tx-Rx就构成了一个空间信道。

设相邻的两个天线之间排布间距为ddd,到达角(angle of arrival,AoA)为 θ\thetaθ,则相邻的两个天线之间会产生一个固定的光程差 dsinθd \sin \thetadsinθ,这个固定的光程差会造成相邻两个信道间接收回波固定的相位差。即
dsinθλ=Δϕ2π\frac{d \sin \theta}{\lambda}=\frac{\Delta \phi}{2\pi} λdsinθ=2πΔϕ
于是我们就有
sinθ=λ2πdΔϕ\sin\theta = \frac{\lambda}{2 \pi d} \Delta \phi sinθ=2πdλΔϕ
最大测量角度
由于
−π<Δϕ<π-\pi<\Delta \phi < \pi −π<Δϕ<π
所以最大测量角度为
θmax<arcsin(λ2d)\theta_{max} < \arcsin (\frac{\lambda}{2d}) θmax<arcsin(2dλ)
取天线阵列间距为λ2\frac{\lambda}{2}2λ时,就可得此时测量达到达到角的范围正好在±90°,即
−1<sinθ<1-1< \sin \theta < 1 −1<sinθ<1
−90∘<θ<90∘-90 ^{\circ} < \theta < 90^{\circ} −90∘<θ<90∘
但值得注意的是,虽然sinθ\sin \thetasinθ与我们的Δϕ\Delta \phiΔϕ成正比,但由于sinθ\sin \thetasinθ 函数本身的非线性,θ\thetaθ 在角度小时对Δϕ\Delta \phiΔϕ更敏感,或者说:在低角度范围(如AoA±30°)内测角的精度(或区分度)更高。
可以看下面的函数图来有一个直观的认识:当我们在sinθ\sin \thetasinθ轴取均匀标度,在θ\thetaθ 轴上的标度随角度的增加是越来越粗的。

相位差的周期性
在之前 测速 的文章中,我们已经讨论过相位差的周期性,及其基于数字域角分辨率下的FFT结果。那么,现在由于N个信道所造成的固定相位差,同样也会形成这个一个相位差的周期性。
借用一幅TI教程的示意图,我们此时对在同一range bin中且又在同一 velocity bin中的两个运动物体进行区分,那么,如果其AoA不同,我们就可以借由 angle FFT 来完成对这两个运动物体的区分。
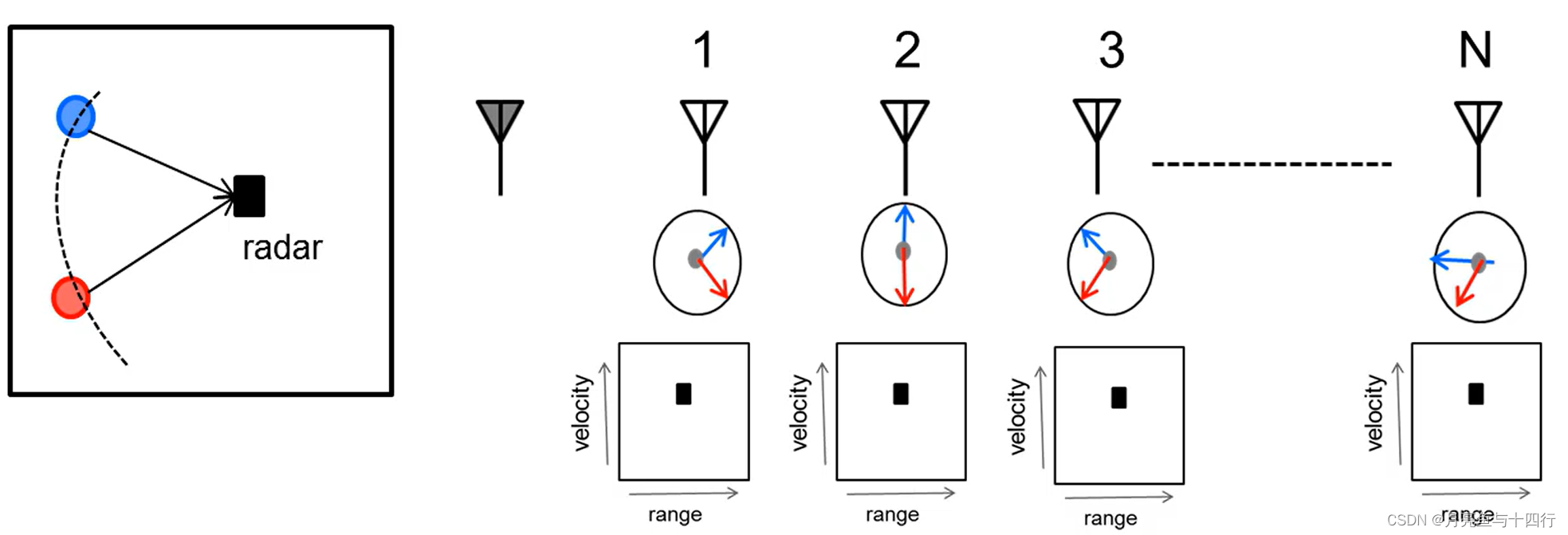
角度分辨率
看得出来,此处的推导与测速中的推导相近。在数字域上的角速度分辨率为
Δω=2πNradians/sampleΔω= \frac{2 \pi}{N} radians/sample Δω=N2πradians/sample
其中N为FFT的点数,继续令Δϕ=w\Delta \phi = wΔϕ=w,则
sin(θ+Δθ)−sin(θ)=λ2πd(Δw+w)−λ2πdw=λ2πdΔw\sin(\theta + \Delta \theta) -\sin(\theta) = \frac{\lambda}{2 \pi d}(\Delta w +w) - \frac{\lambda}{2 \pi d}w = \frac{\lambda}{2 \pi d}\Delta w sin(θ+Δθ)−sin(θ)=2πdλ(Δw+w)−2πdλw=2πdλΔw
根据导数的定义,我们有
sin(θ+Δθ)−sin(θ)Δθ=cosθ\frac{ \sin(\theta + \Delta \theta) -\sin(\theta) }{\Delta \theta}= \cos \theta Δθsin(θ+Δθ)−sin(θ)=cosθ
于是,可进一步推得
cos(θ)Δθ=λ2πdΔw\cos (\theta) \Delta \theta = \frac{\lambda}{2 \pi d}\Delta w cos(θ)Δθ=2πdλΔw
Δθ=λ2πdcos(θ)Δw=λNdcos(θ)\Delta \theta = \frac{\lambda}{2 \pi d \cos (\theta) }\Delta w=\frac{\lambda}{N d \cos (\theta) } Δθ=2πdcos(θ)λΔw=Ndcos(θ)λ
这里同样可对之前低角度范围内测角的精度(或区分度)更高的原因做出解释:cosθ\cos \thetacosθ在低角度时值更大,使得此时的 Δθ\Delta \thetaΔθ 有着更细微的取值。
如果取天线阵列间距为 λ2\frac{\lambda}{2}2λ ,且设 θ=0\theta = 0θ=0,就可以得到通常定义下的最精细的角度分辨率为
θres=2N\theta_{res} = \frac{2}{N} θres=N2
可见其将受限于能够完成多发多收的天线数量。
相关文章:

【FMCW 04】测角-Angle FFT
在之前的文章中,我们已经详尽讨论过FMCW雷达测距和测速的原理,现在来讲最后一块内容,测角。测角对于硬件设备具有要求,即要求雷达具有多发多收结构,从而形成多个空间信道(channel),我…...

Linux操作系统学习(线程同步)
文章目录线程同步条件变量生产者与消费者模型信号量环形队列应用生产者消费者模型线程同步 现实生活中我们经常会遇到同一个资源多个人都想使用的问题,例如游乐园过山车排队,玩完的游客还想再玩,最好的办法就是玩完的游客想再玩就去重新排…...

了解动态规划算法:原理、实现和优化指南
动态规划 详细介绍例子斐波那契数列最长回文子串优化指南优化思路斐波那契数列优化最长回文子串优化详细介绍 动态规划(Dynamic Programming,简称 DP)是一种通过将原问题拆分成子问题并分别求解这些子问题来解决复杂问题的算法思想。 它通常用于求解优化问题,它的核心思想…...

《NFL橄榄球》:明尼苏达维京人·橄榄1号位
明尼苏达维京人(英语:Minnesota Vikings)是一支职业美式足球球队,位于明尼苏达州的明尼阿波利斯。他们现时在国家橄榄球联合会北区参与国家美式足球联盟比赛。该球队本为美国美式足球联盟(AFL)的球队。但是…...
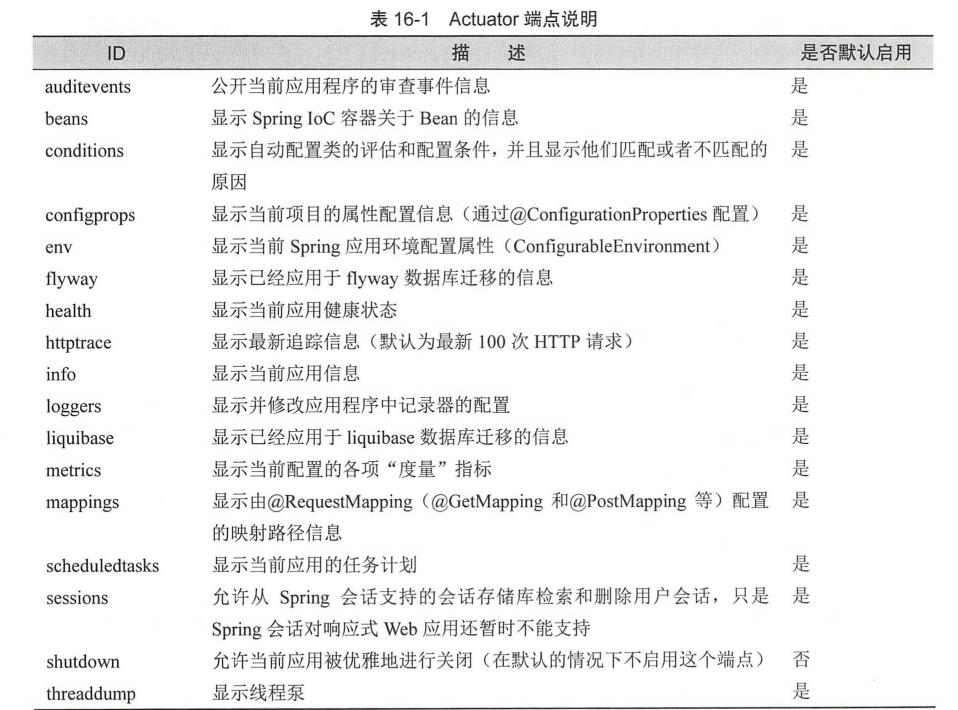
sheng的学习笔记-Actuator健康监控
前言在微服务系统里,对微服务程序的运行状况的跟踪和监控是必不可少的;例如GPE,TelegrafinfluxDB都提供了微服务体系监控的方案, ZIPKIN, Skywalking都提供了微服务云体系的APM的方案; 这些解决方案功能全面…...

初次使用ESP32-CAM记录
模块的配置和图片 摄像头:8225N V2.0 171026 模块esp-32s 参考资料:https://docs.ai-thinker.com/esp32 配置环境 参考:https://blog.csdn.net/weixin_43794311/article/details/128622558 简单使用需要注意的地方 基本的环境配置和串口…...
)
华为OD机试真题Python实现【最长连续交替方波信号】真题+解题思路+代码(20222023)
最长连续交替方波信号 题目 输入一串方波信号,求取最长的完全连续交替方波信号,并将其输出, 如果有相同长度的交替方波信号,输出任一即可,方波信号高位用1标识,低位用0标识 如图: 说明: 一个完整的信号一定以0开始然后以0结尾, 即 010 是一个完整的信号,但101,101…...
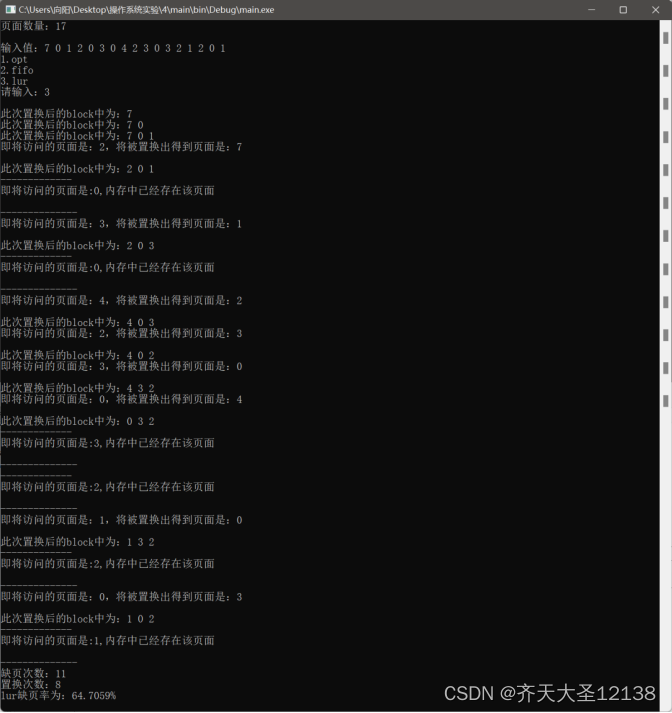
【操作系统原理实验】页面替换策略模拟实现
选择一种高级语言如C/C等,编写一个页面替换算法的模拟实现程序。1) 设计内存管理相关数据结构;2) 随机生成一个页面请求序列;3) 设置内存管理模拟的关键参数;4) 实现该页面置换算法;5) 模拟实现给定配置请求序列的换页…...

Java中解析XML文件
1 在Java中解析XML文件共有四种方式 A、DOM方式解析XML数据 树结构,有助于更好地理解、掌握,代码易于编写,在解析过程中树结构是保存在内存中,方便修改 B、SAX方式解析 采用事件驱动模式,对内存消耗比较小࿰…...
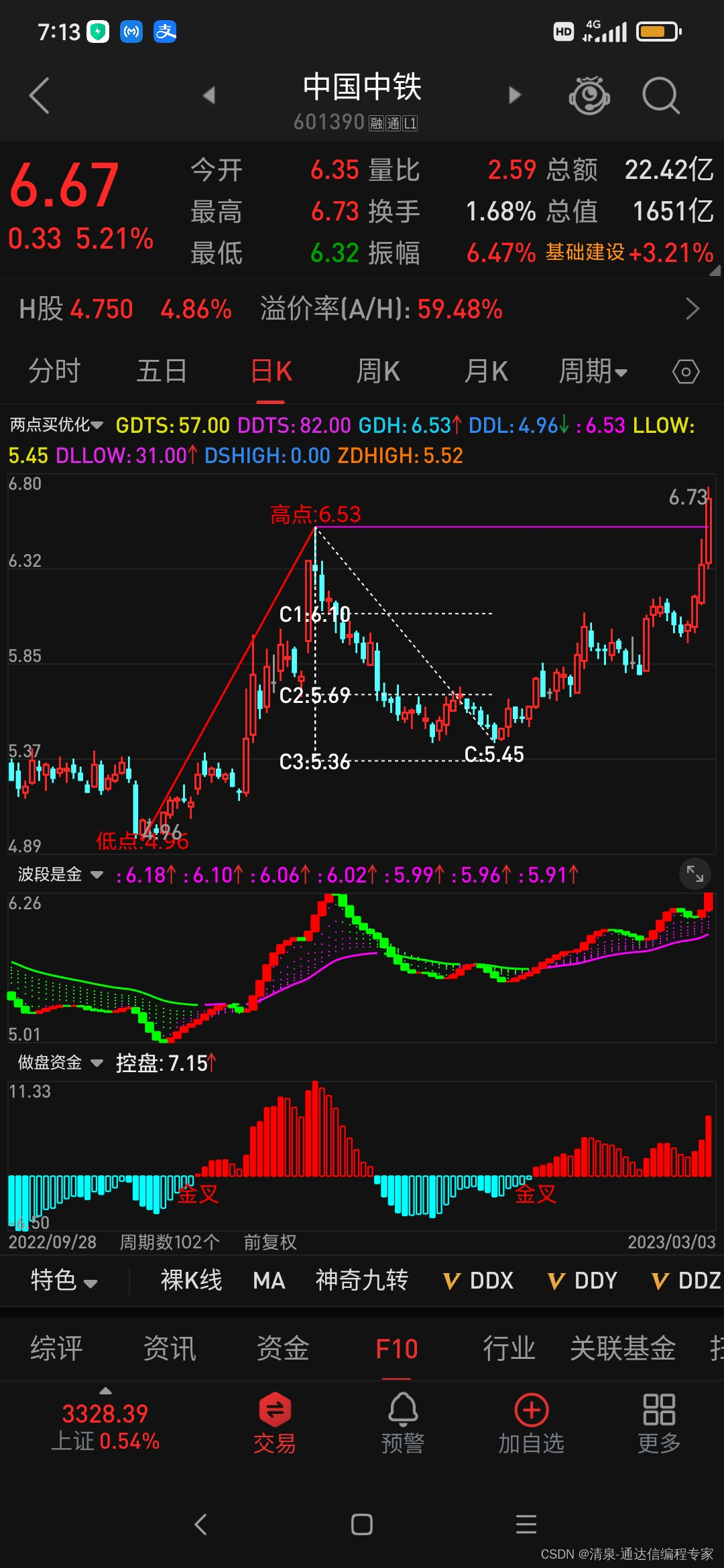
二点回调测买 源码
如图所示,两点回调测买点的效果图,这是我们常见的一种预测买点计算方法。 现将源码公布如下: DRAWKLINE(H,O,L,C); N:13; A1:REF(HIGH,N)HHV(HIGH,2*N1); B1:FILTER(A1,N); C1:BACKSET(B1,N1); D1:FILTER(C1,N); A2:REF(LOW,N)LLV(LOW,2*N1…...
钉钉端H5开发调试怎么搞
H5开发本地调试教程 作为一名前端开发,大家平时工作中或多或少都有接触或需要开发H5页面的场景,在开发过程中,如何像PC端页面一样有有丝滑的体验呢? 不同的情况需要在不同的端调试更方便有效: 1. 在画UI的时候,更适合在PC端调试,更改代码或者直接在浏览器调试,都是实…...
Mysql Server原理简介
Mysql客户端包括JDBC、 Navicat、sqlyog,只是为了和mysql server建立连接,向mysql server提交sql语句。mysql server组件第一部分叫连接器主要承担的功能叫管理连接和验证权限,每次在进行数据库访问的时候,必然要输入用户名和密码…...

23种设计模式-外观模式
外观模式是一种结构型设计模式,它提供了一个统一的接口,用来访问子系统中的一群接口。外观模式定义了一个高层接口,使得客户端可以更加方便地访问子系统的功能。在这篇博客中,我们将讨论如何使用Java实现外观模式,并通…...

使用 Vulkan VkImage 作为 CUDA cuArray
使用 Vulkan VkImage 作为 CUDA cuArray【问题标题】:Use Vulkan VkImage as a CUDA cuArray使用 Vulkan VkImage 作为 CUDA cuArray【发布时间】:2019-08-20 20:01:10【问题描述】:将 Vulkan VkImage 用作 CUDA cuArray 的正确方法是什么&am…...

电商API接口-电商OMS不可或缺的一块 调用代码展示
电商后台管理系统关键的一环就是实现电商平台数据的抓取,以及上下架商品、订单修改等功能的调用。这里就需要调用电商API接口。接入电商API接口后再根据自我的需求进行功能再开发,实现业务上的数字化管理。其中订单管理模板上需要用到如下API:seller_ord…...

Solaris ZFS文件系统rpool扩容
ZFS文件系统简介 Solaris10默认的文件系统是ufs(Unix Filesystem),当然也可以选装zfs;Solaris11默认的文件系统是zfs(Zettabyte Filesystem)。 ZFS文件系统的英文名称为Zettabyte File System,也叫动态文件…...
模式识别 —— 第二章 参数估计
模式识别 —— 第二章 参数估计 文章目录模式识别 —— 第二章 参数估计最大似然估计(MLE)最大后验概率估计(MAP)贝叶斯估计最大似然估计(MLE) 在语言上: 似然(likelihood…...
)
判断4位回文数-课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例1:判断4位回文数 所谓回文数,就是各位数字从高位到低位正序排列和从低位到高位逆序排列都是同一数值的数,例如,数字1221按正序和逆序排列都为1221,因此1221就是一个回文数;而1234的各位按倒序排列是43…...
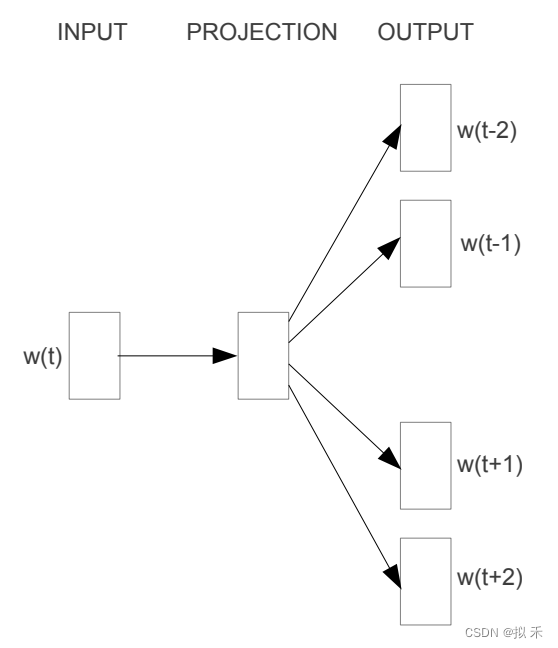
【NLP】Word2Vec 介绍
Word2Vec 是一种非常流行的自然语言处理技术,它将每个单词表示为高维向量,并且通过向量之间的相似度来表示单词之间的语义关系。 1 One-Hot 编码🍂 在自然语言处理任务中,我们需要将文本转换为计算机可以理解的形式,即…...

3月6日,30秒知全网,精选7个热点
///石家庄地铁:在指定店铺购物金额不限 就可免费乘地铁 乘客只要在指定商铺或地铁站内36524便利店购物,便能得到一张当日乘车券,可免费乘坐地铁一次,不限里程 ///神州泰岳:公司语音机器人等产品能够进行多轮问答 公司…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
