C语言经典算法-9
文章目录
- 其他经典例题跳转链接
- 46.稀疏矩阵
- 47.多维矩阵转一维矩阵
- 48.上三角、下三角、对称矩阵
- 49.奇数魔方阵
- 50.4N 魔方阵
- 51.2(2N+1) 魔方阵
其他经典例题跳转链接
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-2
字串核对、双色、三色河内塔、背包问题(Knapsack Problem)、蒙地卡罗法求 PI、Eratosthenes筛选求质数
C语言经典算法-3
超长整数运算(大数运算)、长 PI、最大公因数、最小公倍数、因式分解、完美数、阿姆斯壮数
C语言经典算法-4
最大访客数、中序式转后序式(前序式)、后序式的运算、洗扑克牌(乱数排列)、Craps赌博游戏
C语言经典算法-5
约瑟夫问题(Josephus Problem)、排列组合、格雷码(Gray Code)、产生可能的集合、m元素集合的n个元素子集
C语言经典算法-6
数字拆解、得分排行,选择、插入、气泡排序、Shell 排序法 - 改良的插入排序、Shaker 排序法 - 改良的气泡排序
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵
46.稀疏矩阵
说明
如果在矩阵中,多数的元素并没有资料,称此矩阵为稀疏矩阵(sparse matrix),由于矩阵在程式中常使用二维阵列表示,二维阵列的大小与使用的记忆体空间成正比,如果多数的元素没有资料,则会造成记忆体空间的浪费,为 此,必须设计稀疏矩阵的阵列储存方式,利用较少的记忆体空间储存完整的矩阵资讯。
解法
在这边所介绍的方法较为简单,阵列只储存矩阵的行数、列数与有资料的索引位置及其值,在需要使用矩阵资料时,再透过程式运算加以还原,例如若矩阵资料如下 ,其中0表示矩阵中该位置没有资料:
0 0 0 0 0 0
0 3 0 0 0 0
0 0 0 6 0 0
0 0 9 0 0 0
0 0 0 0 12 0
这个矩阵是5X6矩阵,非零元素有4个,您要使用的阵列第一列记录其列数、行数与非零元素个数:
5 6 4
阵列的第二列起,记录其位置的列索引、行索引与储存值:
1 1 3
2 3 6
3 2 9
4 4 12
所以原本要用30个元素储存的矩阵资讯,现在只使用了15个元素来储存,节省了不少记忆体的使用。
#include <stdio.h>
#include <stdlib.h> int main(void) { int num[5][3] = {{5, 6, 4}, {1, 1, 3}, {2, 3, 6}, {3, 2, 9}, {4, 4, 12}}; int i, j, k = 1; printf("sparse matrix:\n"); for(i = 0; i < 5; i++) { for(j = 0; j < 3; j++) { printf("%4d", num[i][j]); } putchar('\n'); } printf("\nmatrix还原:\n"); for(i = 0; i < num[0][0]; i++) { for(j = 0; j < num[0][1]; j++) { if(k < num[0][2] && i == num[k][0] && j == num[k][1]) { printf("%4d ", num[k][2]); k++; } else printf("%4d ", 0); } putchar('\n'); } return 0;
}
47.多维矩阵转一维矩阵
说明
有的时候,为了运算方便或资料储存的空间问题,使用一维阵列会比二维或多维阵列来得方便,例如上三角矩阵、下三角矩阵或对角矩阵,使用一维阵列会比使用二维阵列来得节省空间。
解法
以二维阵列转一维阵列为例,索引值由0开始,在由二维阵列转一维阵列时,我们有两种方式:「以列(Row)为主」或「以行(Column)为主」。由于 C/C++、Java等的记忆体配置方式都是以列为主,所以您可能会比较熟悉前者(Fortran的记忆体配置方式是以行为主)。
以列为主的二维阵列要转为一维阵列时,是将二维阵列由上往下一列一列读入一维阵列,此时索引的对应公式如下所示,其中row与column是二维阵列索引,loc表示对应的一维阵列索引:
loc = column + row*行数
以行为主的二维阵列要转为一维阵列时,是将二维阵列由左往右一行一行读入一维阵列,此时索引的对应公式如下所示:
loc = row + column*列数
公式的推导您画图看看就知道了,如果是三维阵列,则公式如下所示,其中i(个数u1)、j(个数u2)、k(个数u3)分别表示三维阵列的三个索引:
以列为主:loc = iu2u3 + ju3 + k
以行为主:loc = ku1u2 + ju1 + i
更高维度的可以自行依此类推,但通常更高维度的建议使用其它资料结构(例如物件包装)会比较具体,也不易搞错。
在C/C++中若使用到指标时,会遇到指标运算与记忆体空间位址的处理问题,此时也是用到这边的公式,不过必须在每一个项上乘上资料型态的记忆体大小。
#include <stdio.h>
#include <stdlib.h> int main(void) { int arr1[3][4] = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}}; int arr2[12] = {0}; int row, column, i; printf("原二维资料:\n"); for(row = 0; row < 3; row++) { for(column = 0; column < 4; column++) { printf("%4d", arr1[row][column]); } printf("\n"); } printf("\n以列为主:"); for(row = 0; row < 3; row++) { for(column = 0; column < 4; column++) { i = column + row * 4; arr2[i] = arr1[row][column]; } } for(i = 0; i < 12; i++) printf("%d ", arr2[i]); printf("\n以行为主:"); for(row = 0; row < 3; row++) { for(column = 0; column < 4; column++) { i = row + column * 3; arr2[i] = arr1[row][column]; } } for(i = 0; i < 12; i++) printf("%d ", arr2[i]); printf("\n"); return 0;
}
48.上三角、下三角、对称矩阵
说明
上三角矩阵是矩阵在对角线以下的元素均为0,即Aij = 0,i > j,例如:
1 2 3 4 5
0 6 7 8 9
0 0 10 11 12
0 0 0 13 14
0 0 0 0 15
下三角矩阵是矩阵在对角线以上的元素均为0,即Aij = 0,i < j,例如:
1 0 0 0 0
2 6 0 0 0
3 7 10 0 0
4 8 11 13 0
5 9 12 14 15
对称矩阵是矩阵元素对称于对角线,例如:
1 2 3 4 5
2 6 7 8 9
3 7 10 11 12
4 8 11 13 14
5 9 12 14 15
上三角或下三角矩阵也有大部份的元素不储存值(为0),我们可以将它们使用一维阵列来储存以节省储存空间,而对称矩阵因为对称于对角线,所以可以视为上三角或下三角矩阵来储存。
解法
假设矩阵为nxn,为了计算方便,我们让阵列索引由1开始,上三角矩阵化为一维阵列,若以列为主,其公式为:loc = n*(i-1) - i*(i-1)/2 + j
化为以行为主,其公式为:loc = j*(j-1)/2 + i
下三角矩阵化为一维阵列,若以列为主,其公式为:loc = i*(i-1)/2 + j
若以行为主,其公式为:loc = n*(j-1) - j*(j-1)/2 + i
公式的导证其实是由等差级数公式得到,您可以自行绘图并看看就可以导证出来,对于C/C++或Java等索引由0开始的语言来说,只要将i与j各加1,求得loc之后减1即可套用以上的公式。
#include <stdio.h>
#include <stdlib.h>
#define N 5 int main(void) { int arr1[N][N] = { {1, 2, 3, 4, 5}, {0, 6, 7, 8, 9}, {0, 0, 10, 11, 12}, {0, 0, 0, 13, 14}, {0, 0, 0, 0, 15}}; int arr2[N*(1+N)/2] = {0}; int i, j, loc = 0; printf("原二维资料:\n"); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { printf("%4d", arr1[i][j]); } printf("\n"); } printf("\n以列为主:"); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) { if(arr1[i][j] != 0) arr2[loc++] = arr1[i][j]; } } for(i = 0; i < N*(1+N)/2; i++) printf("%d ", arr2[i]); printf("\n输入索引(i, j):"); scanf("%d, %d", &i, &j); loc = N*i - i*(i+1)/2 + j; printf("(%d, %d) = %d", i, j, arr2[loc]); printf("\n"); return 0;
}
49.奇数魔方阵
说明
将1到n(为奇数)的数字排列在nxn的方阵上,且各行、各列与各对角线的和必须相同,如下所示:
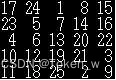
解法
填魔术方阵的方法以奇数最为简单,第一个数字放在第一行第一列的正中央,然后向右(左)上填,如果右(左)上已有数字,则向下填,如下图所示:
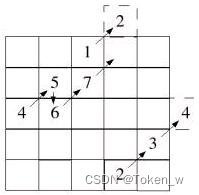
一般程式语言的阵列索引多由0开始,为了计算方便,我们利用索引1到n的部份,而在计算是向右(左)上或向下时,我们可以将索引值除以n值,如果得到余数为1就向下,否则就往右(左)上,原理很简单,看看是不是已经在同一列上绕一圈就对了。
#include <stdio.h>
#include <stdlib.h> #define N 5 int main(void) { int i, j, key; int square[N+1][N+1] = {0}; i = 0; j = (N+1) / 2; for(key = 1; key <= N*N; key++) { if((key % N) == 1) i++; else { i--; j++; } if(i == 0) i = N; if(j > N) j = 1; square[i][j] = key; } for(i = 1; i <= N; i++) { for(j = 1; j <= N; j++) printf("%2d ", square[i][j]); } return 0;
}
50.4N 魔方阵
说明
与 奇数魔术方阵 相同,在于求各行、各列与各对角线的和相等,而这次方阵的维度是4的倍数。
解法
先来看看4X4方阵的解法:
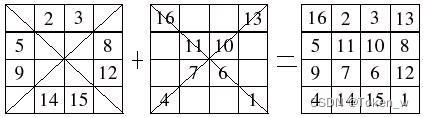
简单的说,就是一个从左上由1依序开始填,但遇对角线不填,另一个由左上由16开始填,但只填在对角线,再将两个合起来就是解答了;如果N大于2,则以 4X4为单位画对角线:
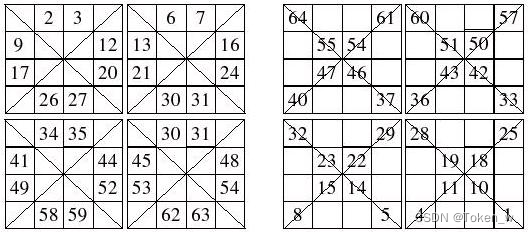
至于对角线的位置该如何判断,有两个公式,有兴趣的可以画图印证看看,如下所示:
左上至右下:j % 4 == i % 4
右上至左下:(j % 4 + i % 4) == 1
#include <stdio.h>
#include <stdlib.h> #define N 8 int main(void) { int i, j; int square[N+1][N+1] = {0}; for(j = 1; j <= N; j++) { for(i = 1; i <= N; i++){ if(j % 4 == i % 4 || (j % 4 + i % 4) == 1) square[i][j] = (N+1-i) * N -j + 1; else square[i][j] = (i - 1) * N + j; } } for(i = 1; i <= N; i++) { for(j = 1; j <= N; j++) printf("%2d ", square[i][j]); printf("\n"); } return 0;
}
51.2(2N+1) 魔方阵
说明方阵的维度整体来看是偶数,但是其实是一个奇数乘以一个偶数,例如6X6,其中6=2X3,我们也称这种方阵与单偶数方阵。
解法如果您会解奇数魔术方阵,要解这种方阵也就不难理解,首先我们令n=2(2m+1),并将整个方阵看作是数个奇数方阵的组合,如下所示:
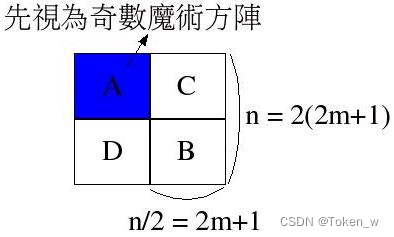
首先依序将A、B、C、D四个位置,依奇数方阵的规则填入数字,填完之后,方阵中各行的和就相同了,但列与对角线则否,此时必须在A-D与C- B之间,作一些对应的调换,规则如下:
将A中每一列(中间列除外)的头m个元素,与D中对应位置的元素调换。
将A的中央列、中央那一格向左取m格,并与D中对应位置对调
将C中每一列的倒数m-1个元素,与B中对应的元素对调
举个实例来说,如何填6X6方阵,我们首先将之分解为奇数方阵,并填入数字,如下所示:
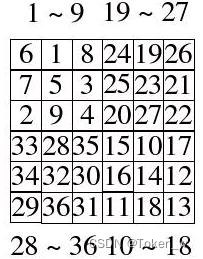
接下来进行互换的动作,互换的元素以不同颜色标示,如下:
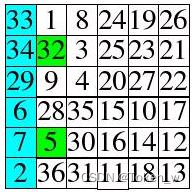
由于m-1的数为0,所以在这个例子中,C-B部份并不用进行对调。
#include <stdio.h>
#include <stdlib.h> #define N 6
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void magic_o(int [][N], int);
void exchange(int [][N], int); int main(void) { int square[N][N] = {0}; int i, j; magic_o(square, N/2); exchange(square, N); for(i = 0; i < N; i++) { for(j = 0; j < N; j++) printf("%2d ", square[i][j]); printf("\n"); } return 0;
} void magic_o(int square[][N], int n) { int count, row, column; row = 0; column = n / 2; for(count = 1; count <= n*n; count++) { square[row][column] = count; // 填A square[row+n][column+n] = count + n*n; // 填B square[row][column+n] = count + 2*n*n; // 填C square[row+n][column] = count + 3*n*n; // 填D if(count % n == 0) row++; else { row = (row == 0) ? n - 1 : row - 1 ; column = (column == n-1) ? 0 : column + 1; } }
} void exchange(int x[][N], int n) { int i, j; int m = n / 4; int m1 = m - 1; for(i = 0; i < n/2; i++) { if(i != m) { for(j = 0; j < m; j++) // 处理规则 1 SWAP(x[i][j], x[n/2+i][j]); for(j = 0; j < m1; j++) // 处理规则 2 SWAP(x[i][n-1-j], x[n/2+i][n-1-j]); } else { // 处理规则 3 for(j = 1; j <= m; j++) SWAP(x[m][j], x[n/2+m][j]); for(j = 0; j < m1; j++) SWAP(x[m][n-1-j], x[n/2+m][n-1-j]); } }
}
系列好文,点击链接即可跳转
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法
相关文章:

C语言经典算法-9
文章目录 其他经典例题跳转链接46.稀疏矩阵47.多维矩阵转一维矩阵48.上三角、下三角、对称矩阵49.奇数魔方阵50.4N 魔方阵51.2(2N1) 魔方阵 其他经典例题跳转链接 C语言经典算法-1 1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6.…...

React 19的变化
并发模式(非实验): React 的并发模式终于从实验阶段毕业了。这一改变游戏规则的功能允许 React 应用程序同时准备多个版本的 UI。有着更平滑的过渡和更灵敏的用户体验,因为 React 现在可以处理高优先级更新,同时保持应用程序的交互…...
的区别是什么?)
Kafka整理-Kafka与传统消息队列系统(如RabbitMQ, ActiveMQ)的区别是什么?
Apache Kafka与传统消息队列系统(如RabbitMQ, ActiveMQ)虽然都是处理消息和数据流的中间件,但它们在设计理念、架构、功能和使用场景方面有显著的区别。下面是Kafka与传统消息队列系统的主要区别: 1. 设计目的和使用场景 Kafka: 设计初衷是为处理大量的实时数据流。强调高…...
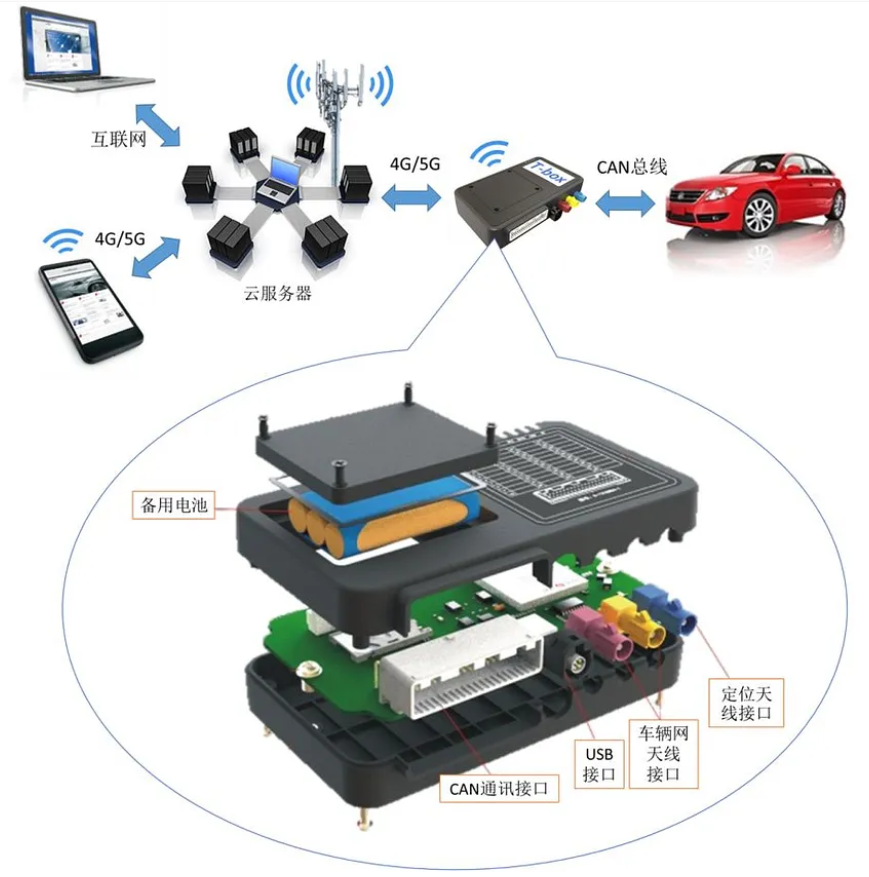
汽车电子零部件(8):T_Box
前言: 网联汽车(Connected Vehicles ,CV)是一个广泛的概念,四个主要的CV线程已发展起来:互联、自主、共享和电动。这些应用于包括CV在内的垂直领域:汽车、通信、互联网和共享手机服务。中国汽车工程师学会(SAEC)提倡将车载ADAS(高级驾驶员辅助系统)与通信技术相结合…...

数库据设计最佳实践
中老年程序员,从业生涯设计过很多数据库,有用上的也有没用上的,有精心设计花无数心思更改了无数次的也有敷衍了事能用就行的,有最糟糕的设计也有感觉还不错的。在设计和修改过程中有很多疑问和感悟,在此记录一下以方便…...

ESSBAE 数据挖掘
essbase数据挖掘框架 1.算法:用来分析数据的方法 2.模型:系列的算法集合 3.任务:数据挖掘的步骤 4.任务模板,可以重复执行的任务 数据挖掘任务: 明确任务 建立及训练模型 测试模型 执行任务 为模型打分 ess…...
上的文件可双向复制粘贴)
在Linux/Ubuntu/Debian中使用iFuse访问iOS 设备(例如 iPhone 或 iPad)上的文件可双向复制粘贴
iFuse 是一款工具,可让你在 Linux 系统上安装 iOS 设备(例如 iPhone 或 iPad),使你能够访问其文件系统并与设备传输文件。 以下是有关如何使用 iFuse 的基本指南: 安装依赖项:在安装 iFuse 之前,…...

驱动开发中的DMA是什么
DMA是一种无须CPU的参与就可以让外设与系统内存之间进行双向数据传输的硬件机制。 使用DMA可以使系统CPU从实际的I/O数据传输过程中摆脱出来, 从而大大提高系统的吞吐率。 DMA通常与硬件体系结构, 特别是外设的总线技术密切相关。 DMA方式的数据传输由DM…...

websocket 升级协议时的协议切换点
websocket 的 rfc6455 标准中提到了协议升级,从http协议升级到websocket协议,用的办法是在http的request header中包含Connection: upgrade 和 Upgrade: websocket 以及其他验证相关的头。服务器验证通过后发送 respond,并升级到websocket。但…...

在Linux中开发C++
在Linux中开发C 本文档为本人在学习慕课网课程——[重学C ,重构你的C知识体系]时的一些记录与思考,侵删。学习课程请支持正版! 1. 搭建C/C编译环境 1.1 gcc 和 g 的区别 本质上没有太大区别,gcc 默认使用 c 编译器…...

【linux】Debian访问Debian上的共享目录
要在Debian系统上访问共享目录,通常意味着要访问通过网络共享的文件夹,比如通过SMB/CIFS(Server Message Block/Common Internet File System)协议共享的Windows共享文件夹。以下是访问共享目录的步骤: 1. 安装必要的…...
Postman Newman API 自动化测试快速入门
什么是 Newman? Newman 是一款专为 Postman 打造的命令行工具,旨在通过自动运行 Postman 集合和环境,实现 API 测试的自动化。它使得开发者无需打开 Postman 图形界面,即可直接在命令行中执行测试用例。 Newman 的优势 使用 Ne…...

Python之Web开发中级教程----ubuntu安装MySQL
Python之Web开发中级教程----ubuntu安装MySQL 进入/opt目录 cd /opt 更新软件源 sudo apt-get upgrade sudo apt-get update 3、安装Mysql server sudo apt-get install mysql-server 4、启动Mysql service mysql start 5、确认Mysql的状态 service mysql status 6、安全设…...
Flutter开发入门——路由
什么是路由? 移动端应用开发中,路由技术是一个非常重要的组成部分。路由技术负责管理应用中各个页面之间的跳转、导航以及参数传递等关键功能。在移动端应用中,一个高效、易于维护的路由系统对于提高开发效率和用户体验具有重要意义。 Flut…...
Acrobat Pro DC 2023:PDF编辑与管理的全新体验
Acrobat Pro DC 2023是一款功能强大且全面的PDF编辑和管理软件,旨在为用户提供卓越的PDF处理体验。以下是关于Acrobat Pro DC 2023软件功能特色的详细介绍: PDF编辑和管理:Acrobat Pro DC 2023拥有强大的PDF编辑功能,可以对PDF文…...

Linux课程_____网络管理
一、查看接口信息 1. ifconfig 查看所有活动网络接口的信息 ifconfig -a 查看所有网络接口信息 ifconfig 直接加网络接口 查看指定网络接口信息 1.1查看指定接口IP [rootlocalhost ~]# ip addr show ens160 1.2设置网络接口的IP地址 # ifconfig eth0 192.168.152.133 …...
ubuntu20.04_PX4_1.13
说在前面:(最好找一个干净的Ubuntu系统)如果配置环境的过程中出现很多编译的错误或者依赖冲突,还是建议新建一个虚拟机,或者重装Ubuntu系统,这样会避免很多麻烦💐 , 安装PX4 1.13.2 …...

12350安全生产举报热线系统解决方案
一、建设背景 1. 安全生产的重要性 在当今社会,安全生产是企业和社会发展中至关重要的一环。随着工业化的推进和技术的不断创新,各种生产活动中潜在的安全隐患也随之增加。为了及时发现和解决这些问题,各省市纷纷设立了安全生产举报热线。在…...
上篇)
Java 多线程(超详细讲解)上篇
多线程可以使程序在同一时间内执行多个操作,采用Java中的多线程机制可以使计算机资源得到更充分的利用,多线程技术在网络编程中有广泛的应用。一、进程与线程 进程是程序的一次动态执行过程,它是从代码加载、执行中到执行完毕的一个完整过程…...
15届蓝桥杯备赛(2)
文章目录 刷题笔记(2)二分查找在排序数组中查找元素的第一个和最后一个位置寻找旋转排序数组中的最小值搜索旋转排序数组 链表反转链表反转链表II 二叉树相同的树对称二叉树平衡二叉树二叉树的右视图验证二叉搜索树二叉树的最近公共祖先二叉搜索树的最近公共祖先二叉树层序遍历…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
