算法学习(持续更新中)
学习视频:一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解(马士兵)_哔哩哔哩_bilibili
时间复杂度
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中发生了多少常数操作,进而总结出常数操作数量的表达式。
在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果为f(N),那么时间复杂度就位O(f(N))。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”.
常数操作:例如数组根据索引寻值,加、减、乘、除、比较
排序
选择排序
每次选择 i 到 n-1 范围内值最小的索引位置 t ,每一次内层循环结束之后交换 i 和 t 索引位置上的值,每一次外层循环 i 的值加 1
private static void selectSort(Integer[] nums) {for(int i=0;i<nums.length-1;i++){int t=i;for(int j=i+1;j<nums.length;j++){if(nums[t]>nums[j]){t=j;}}swap(nums,i,t);}}时间复杂度:O(n^2) ,空间复杂度:O(1)
冒泡排序
每次从 0 到 i 的范围中将相邻的值进行两两比较,将大的一个值移到后面,这样每一次内层循环结束后,i 位置的值就是0 到 i 范围内最大的值,每一次外层循环 i 的值减 1.
private static void BubbleSort(Integer[] nums) {int n=nums.length;for(int i=n-1;i>0;i--){for(int j=0;j<i;j++){if(nums[j]>nums[j+1]){swap(nums, j, j+1);}}}}时间复杂度:O(n^2) ,空间复杂度:O(1)
插入排序
i 从 0 开始,维护一个 0 到 i 范围的有序数组,每一次 i++ ,令 j 等于 i,j 所在位置的元素 和 j-1 所在位置的元素进行比较 因为前 j-1 个元素是有序的,所以 j 就往前进行比较,如果 j 所在位置 比 j-1 小,就进行交换,再往前进行比较,知道比前面的大为止。
private static void MySort(Integer[] nums) {if(nums==null || nums.length<2){return;}int l=nums.length;for(int i=1;i<l;i++){for(int j=i;j>0;j--){if(nums[j]<nums[j-1]){swap(nums,j,j-1);}else{break;}}}}最坏情况下 时间复杂度为 O(n^2),空间复杂度为O(1)
归并排序
将一个数组分为左右两个子数组,先将这两个子数组分别排好序,再融合,使得父数组也有序。
public static void mergeSort(int[] arr,int l,int r){if(l==r) return;process(arr,l,r);}
private static void process(int[] arr, int l, int r) {if(l==r) return;int mid=l+((r-l)>>1);process(arr,l,mid);process(arr,mid+1,r);merge(arr,l,mid,r);}
private static void merge(int[] arr, int l, int m, int r) {int[] help=new int[r-l+1];int p1=l;int p2=m+1;int i=0;while(p1<=m && p2<=r){help[i++]=arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];}while(p1<=m){help[i++]=arr[p1++];}while (p2<=r){help[i++]=arr[p2++];}for (int j = 0; j < help.length; j++) {arr[l+j]=help[j];}}根据master公式可以得到:
T(N) = 2T(N/2)+O(N) --> 每一次将父函数分成两个数据量为父函数一半的子函数,mergn函数的时间复杂度为O(N) 所以:log(a,b)==d-->log(2,2)==1 所以归并排序的时间复杂度为:O(N*logN),空间复杂度:O(N)
归并排序的扩展
1)小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和
例如:[1,3,4,2,5]:左边比1小的数,没有,为0;3左边比3小的数,1个1;4左边比4小的数:1 * 1+1 * 3=4;2左边比2小的数:1个1;5左边比5小的数:1+3+4+2=10;所以小和为:0+1+4+1+10=16。
也可以看一个数右边有几个比他大的数:1右边有4个数比他大,1 * 4=4;3右边有两个数比他大,2 * 3=6;4右边有1个数比他大,1 * 4=4;2右边有1个数比他大,1 * 2=2;5右边没有比他大的数 ,0;所以小和为:4+6+4+2+0=16。
代码实现:
public static int smallSum(int[] arr,int l,int r){if(l==r) return 0;return process(arr,l,r);}
private static int process(int[] arr, int l, int r) {if(l==r) return 0;int mid=l+((r-l)>>1);return process(arr,l,mid) + process(arr,mid+1,r) + merge(arr,l,mid,r);}
private static int merge(int[] arr, int l, int m, int r) {int[] help=new int[r-l+1];int p1=l;int p2=m+1;int i=0;int res=0;while(p1<=m && p2<=r){//判断右边数组中有几个比左边数组当前p1下标下的数大,计算和res+=arr[p1]<arr[p2]?(r-p2+1)*arr[p1]:0;//在merge的时候,当右边数组p2下标对应的数跟左边数组p1下标对应的数相等的时候,先把右边数组的数加入到临时数组中,因为在去掉了右边与左边相等的数之后,才能得到右边比左边大的数的数量。help[i++]=arr[p1]<arr[p2]?arr[p1++]:arr[p2++];}while(p1<=m){help[i++]=arr[p1++];}while (p2<=r){help[i++]=arr[p2++];}for (int j = 0; j < help.length; j++) {arr[l+j]=help[j];}return res;}流程图:

2)逆序对问题
在一个数组中,左边的数如果比右边的数大,则拆两个数构成一个逆序对,请打印所有逆序对。
代码:
//int[] arr={3,2,4,5,1};
private static int merge(int[] arr, int l, int m, int r) {int[] help=new int[r-l+1];int p1=l;int p2=m+1;int i=0;int res=0;while(p1<=m && p2<=r){//在 1)的代码上加入这一段判断逻辑,就可以打印出所有的逆序对if(arr[p1]>arr[p2]){int p11=p1;while(p11<=m){System.out.println("["+arr[p11++]+" "+arr[p2]+"]");}}res+=arr[p1]<arr[p2]?(r-p2+1)*arr[p1]:0;//这里与 1)有差别,当左边和右边相等的时候,移动左边的help[i++]=arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];}while(p1<=m){help[i++]=arr[p1++];}while (p2<=r){help[i++]=arr[p2++];}for (int j = 0; j < help.length; j++) {arr[l+j]=help[j];}return res;}运行结果:
[3 2]
[5 1]
[2 1]
[3 1]
[4 1]快速排序
思考问题
1)给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组右边。要求额外空间复杂度为O(1),时间复杂度为O(N)。
思路:定义一个小于等于区,初始下标为-1,i 从0开始遍历数组,可以分为两种情况 (1)arr[i] <= num,nums[i]和小于等于区的下一个数交换,小于区右扩,i++。(2)arr[i] > num,i++。
代码:
//arr={3,4,6,7,5,3,5,8},num=5
public static void func1(int[] arr,int num){int i=0;int left=-1;while(i<arr.length){if(arr[i]<=num){swap(arr,++left,i++);}else if(arr[i]>num){i++;}}System.out.println(Arrays.toString(arr));}运行结果:
[0, 0, 5, 3, 5, 7, 6, 8]2)荷兰国旗问题:给定一个数组arr,和一个数num,请把小于num的数放在数组的左边。等于num的数放在数组的中间,大于num的数放在数组的右边,要求额外空间复杂度为O(1),时间复杂度O(N)。
思路:定义一个小于区,初始下标为-1;定义一个大于区,初始下标为arr.length,i 从0开始遍历数组,有三种情况:(1)arr[i] < num ,nums[i]和小于区的下一个数交换,小于区右扩,i++。(2)arr[i] = num ,i++。(3)arr[i] > num ,交换 num[i] 和大于区前一个数,大于区左扩。
代码:
//arr={3,4,6,7,5,3,5,8},num=5
public static void func2(int[] arr,int num){int i=0;int left=-1;int right=arr.length;while (i<right){if(arr[i]<num){swap(arr,++left,i++);}else if(arr[i]==num){i++;}else{swap(arr,--right,i);}}System.out.println(Arrays.toString(arr));}运行结果:
[0, 0, 3, 5, 5, 7, 8, 6]快排1.0
使用思考1)的方式,每次确认一个数的位置
public static void quickSort(int[] arr){if(arr==null || arr.length<2){return;}quickSort(arr,0,arr.length-1);}
public static void quickSort(int[] arr,int l,int r){if(l<r){//r所在位置的元素作为基准点int i = partition(arr, l, r);quickSort(arr,l,i);quickSort(arr,i+1,r);}}
public static int partition(int[] arr, int l, int r){int left=l-1;while(l<r){if(arr[l]<=arr[r]){swap(arr,++left,l++);}else if(arr[l]>arr[r]){l++;}}swap(arr,left+1,r);//left是小于区的边界return left;}对于数组:arr={1,2,3,4,5,6,7,8,9},最坏时间复杂度为O(N^2)
快排2.0
使用 思考 2) 的方式,每次确认一种数的位置
代码:
public static void quickSort(int[] arr){if(arr==null || arr.length<2){return;}quickSort(arr,0,arr.length-1);}//选择数组中最后一位为 基准点public static void quickSort(int[] arr,int l,int r){if(l<r){//p的大小为2,是与最后一位数相等的数的左右边界int[] p=partition(arr,l,r);//左边继续quickSort(arr,l,p[0]-1);//右边继续quickSort(arr,p[1]+1,r);}}
private static int[] partition(int[] arr, int l, int r) {int[] p=new int[2];//小于区域边界int less=l-1;//大于区域边界int more=r;//当l达到大于边界时说明已经分类完成while(l<more){//l所在位置比基准点位置小,arr[l]和小于区的下一个数交换,小于区右扩,l++if(arr[l]<arr[r]){swap(arr,++less,l++);}else if(arr[l]==arr[r]){l++;}else{//arr[l]>arr[r],l位置上的值与大于区前一个位置上的值进行交换,大于区左扩swap(arr,--more,l);}}//基准点所在当前数组的最后一位r,和大于arr[r]上的第一个值的位置(也就是大于区的边界)进行交换。swap(arr,r,more);p[0]=less+1;//等于基准点的数的左边界p[1]=more;//等于基准点的数的有边界//此时:l~less 就是比基准点小的数,more+1~r就是比基准点大的数return p;}如果我们选择的数组为 arr={1,2,3,4,5,6,7,8,9},那么最坏的时间复杂度为O(N^2),
快排3.0
就是在快排2.0的基础上添加了一个随机交换的操作,保证不能人为的列出最坏执行情况
代码:
//int[] arr={3,4,6,7,5,3,5,8};public static void quickSort(int[] arr){if(arr==null || arr.length<2){return;}quickSort(arr,0,arr.length-1);}//选择数组中最后一位为 基准点public static void quickSort(int[] arr,int l,int r){if(l<r){//随机选择一个位置的值与最后一位交换swap(arr,r,l+(int)(Math.random()*(r-l+1)));//p的大小为2,是与最后一位数相等的数的左右边界int[] p=partition(arr,l,r);//左边继续quickSort(arr,l,p[0]-1);//右边继续quickSort(arr,p[1]+1,r);}}
private static int[] partition(int[] arr, int l, int r) {int[] p=new int[2];//小于区域边界int less=l-1;//大于区域边界int more=r;//当l达到大于边界时说明已经分类完成while(l<more){//l所在位置比基准点位置小,arr[l]和小于区的下一个数交换,小于区右扩,l++if(arr[l]<arr[r]){swap(arr,++less,l++);}else if(arr[l]==arr[r]){l++;}else{//arr[l]>arr[r],l位置上的值与大于区前一个位置上的值进行交换,大于区左扩swap(arr,--more,l);}}//基准点所在当前数组的最后一位r,和大于arr[r]上的第一个值的位置(也就是大于区的边界)进行交换。swap(arr,r,more);p[0]=less+1;//等于基准点的数的左边界p[1]=more;//等于基准点的数的有边界//此时:l~less 就是比基准点小的数,more+1~r就是比基准点大的数return p;}运行结果:
[3, 3, 4, 5, 5, 6, 7, 8]时间复杂度:O(N*log(N))
堆排序
代码:
/**int[] arr={4,2,3,1,7};heapSort(arr);System.out.println(Arrays.toString(arr));**/
/*** 堆排序* @param arr 待排序的数组* 时间复杂度:O(N*log(N))* 空间复杂度:O(1)*/public static void heapSort(int[] arr){if(arr==null || arr.length<2){return;}//先调用heapInsert将数组变为大根堆的结构for (int i = 0; i < arr.length; i++) { //O(N)heapInsert(arr,i);//O(log(N))}
//如果仅仅是将数组变成大根堆结构的话,这段代码要快一些
// for(int i=arr.length-1;i>=0;i--){
// heapify(arr,i,arr.length);
// }/*** 然后每一次将堆的最大值(所在位置为0)与最后一个元素互换,堆的长度减1,然后使用heapify调整堆结构,* 这样,数组就从后往前依次有序起来了**/int heapSize=arr.length;swap(arr,0, --heapSize);while (heapSize>0){ //O(N)heapify(arr,0,heapSize);//O(log(N))swap(arr,0,--heapSize);//O(1)}}
/*** index上的值满足大顶堆的条件从下往上移动* @param arr 数组* @param index 要移动的元素* 时间复杂度取决于树的高度:O(logN)*/public static void heapInsert(int[] arr,int index){//index和index的父节点进行比较,如果arr[index]>arr[(index-1)/2],说明它比父节点的值要大,就交换这父子元素的位置。否则,while循环结束//当index=0的时候,(index-1)/2 =0,此时的条件不满足,while循环就结束while(arr[index]>arr[(index-1)/2]){swap(arr,index,(index-1)/2);index=(index-1)/2;}}
/*** index 上的值满足大顶堆的条件从上往下移动* @param arr 数组* @param index 要移动的元素* @param heapSize 堆的大小* 时间复杂度取决于树的高度:O(logN)*/public static void heapify(int[] arr,int index,int heapSize){//当前节点的左孩子节点int left=2*index+1;//当左孩子节点存在的时候while (left<heapSize){//选择左孩子和右孩子中大的一个int largest=(left+1) < heapSize && arr[left+1]>arr[left]?(left+1):left;//选择父节点和孩子节点之间大的一个largest=arr[largest]>arr[index]?largest:index;//如果父节点是大的一个,说明已经满足大顶堆的条件,breakif(largest==index){break;}//交换父节点和孩子节点的值swap(arr,index,largest);//移动到交换后的孩子节点index=largest;//当前节点的左孩子节点left=index*2+1;}}
public static void swap(int[] arr,int i,int j){int tmp=arr[i];arr[i]=arr[j];arr[j]=tmp;}运行结果:
[1, 2, 3, 4, 7]桶排序(基数排序)
代码:
/*** int[] arr={1,21,32,14,57,83,64,100,101};* radixSort(arr);* System.out.println(Arrays.toString(arr));**/public static void radixSort(int[] arr){if(arr==null || arr.length<2){return;}//maxbits(arr) 获取数组中最大数的长度radixSort(arr,0,arr.length-1,maxbits(arr));}
private static void radixSort(int[] arr, int L, int R, int digit) {//10进制final int radix=10;int i=0,j=0;//有多少个数就准备多少个辅助空间int[] bucket=new int[R-L+1];for(int d=1;d<=digit;d++){//有多少位就进出几次/***10个空间* count[0] 当前(d位)是0的数字有多少个* count[1] 当前(d位)是(0~1)的数字有多少个* count[2] 当前(d位)是(0~2)的数字有多少个* count[3] 当前(d位)是(0~3)的数字有多少个* count[i] 当前(d位)是(0~i)的数字有多少个**/int[] count=new int[radix]; //count[0....9]for(i=L;i<=R;i++){//j=获取当前arr[i]的第d位(个、十、百、千.....)数的值j=getDigit(arr[i],d);//对应第j位上的数加1。(0~9)count[j]++;}for(i=1;i<radix;i++){//count[i]=数组中的数在第d位上小于等于i的有多少count[i]+=count[i-1];}//从数组的右边开始遍历for(i=R;i>=L;i--){j=getDigit(arr[i],d);//进桶bucket[count[j]-1]=arr[i];count[j]--;}for(i=L,j=0;i<=R;i++,j++){arr[i]=bucket[j];}}}
private static int getDigit(int i, int d) {int res=0;while(d--!=0){res=i%10;i/=10;}return res;}
private static int maxbits(int[] arr) {int max=Integer.MIN_VALUE;for (int i = 0; i < arr.length; i++) {max=Math.max(max,arr[i]);}int res=0;while (max!=0){res++;max/=10;}return res;}运行结果:
[1, 14, 21, 32, 57, 64, 83, 100, 101]时间复杂度:O(N),空间复杂度:O(N)

排序算法的稳定性
稳定性:同样的个体之间,如果不因为排序而改变相对次序,那这个排序就是具有稳定性的,否则就没有。
稳定性对于基本数据类型的数据没有什么作用,但是对于引用类型的数据在排序的时候就有用了,比如一个商品具有价格与好评这两个属性,我们先根据价格排序,然后根据好评排序,如果排序的算法是具有稳定性的,那么就可以形成一个物美价廉的商品排序。
| 排序算法 | 时间复杂度 | 空间复杂度 | 是否可以实现稳定性 |
|---|---|---|---|
| 选择排序 | O(N^2) | O(1) | 否 |
| 冒泡排序 | O(N^2) | O(1) | 可 |
| 插入排序 | O(N^2) | O(1) | 可 |
| 归并排序 | O(N*log(N)) | O(N) | 可 |
| 快排(随机) | O(N*log(N)) | O(log(N)) | 否 |
| 堆排 | O(N*log(N)) | O(1) | 否 |
| 桶排 | O(N) | O(N) | 可 |
目前还没有找到时间复杂度O(N*log(N)),额外空间复杂度O(1),有可以实现稳定性的排序算法。
异或运算
异或运算 也叫做无进位运算,当两个操作数相同时,异或运算的结果为 0。当两个操作数不同时,异或运算的结果为 1。
1011 ^ 1001 = 0010 , 0 ^ N = N , N ^ N = 0
1 0 1 11 0 0 1= 0 0 1 0//异或操作满足交换律和结合率:a^b=b^aa^bc=a^(b^c)当交换两个数的值时,可以使用异或操作,这样就不会产生额外的空间
@Testpublic void swap(){int a=1;int b=2;
a=a^b;b=a^b;a=a^b;System.out.println("a="+a+"\n"+"b="+b);}
输出:a=2b=1原因:
a=1,b=2 第一次异或: a=a^b,b=b ---> a=1^2,b=1 第二次异或: a=a^b,b=a^b^b=a ---> a=1^2,b=1^2^2-->因为2^2=0,所以b=1^0=1 第三次异或: a=a^b^a,b=a ---> a=1^2^1(原本是a^b^b,因为后面一个b在第二步异或的时候变成了a的值,所以这里是1)-->a=1^1^2=0^2=2 所以a和b就完成了交换。
但是:使用异或操作完成的交换功能在程序中只能作用于地址位置不同的两个对象,如果是同一个地址位置来进行异或,会把值抹为0
例:存在一个int类型的数组
(1)其中有一种数出现了奇数次,其余都出现了偶数次,求这个奇数次的数 (使用时间复杂度为 (O(n),空间复杂度为O(1))。
使用一个整数0,对数组中的每一个数进行异或运算,因为异或运算不在乎数的顺序,所以就是 0 ^ 所有的偶数次的数(为0)^ 奇数次的数(剩一个) ---> 结果就是 0 ^ 一个奇数次的数 = 奇数次的数。
//int[] nums=new int[]{0,0,1,3,1,2,3};
public static void printOddTimesNum1(int[] nums){int eor=0;for (int num : nums) {eor=eor^num;}System.out.println(eor);}
/**输出为:2
**/(2)有两种数出现了奇数次,其余都出现了偶数次,求这个偶数次的数
//int[] nums=new int[]{0,1,3,1,2,3};
public static void printOddTimesNum2(int[] nums){int eor=0;/**eor = 奇数1 ^ 奇数2,因为奇数1和奇数2不相同,所以eor一定不等于0,这表示eor的32位二进制中至少有一位为1.那么在为1的这个二进制位置上,奇数1和奇数2的值一定不同(一定是其中一个为1,另一个为0),所以我们就可以先求出这个位 置,然后再去与数组中的值进行异或,得到其中一个奇数**/for (int num : nums) {eor=eor^num;}/**这里就是来求出最右边为1的位置例如:eor = 10100 ~eor = 01011 ~eor+1 = 01100eor & ~eor+1 : 1010001100---> 00100所以最右边为1的位置就是00100(4)**/int rightIndex=eor & ~eor+1;int onlyOne=0;for (int num : nums) {if((num & rightIndex)==1){//如果右边第4为为1才进行异或运算,onlyOne最后得到的就是奇数1或者奇数2的值onlyOne = onlyOne^num;}}System.out.println("num1:"+onlyOne+"\n"+"num2:"+(eor ^ onlyOne));}
//输出: num1:0
// num2:2二分查找
1)在一个有序数组中,找某个数是否存在
//int res=binarysearch(nums,target,0,nums.length-1);
private static int binarysearch(Integer[] nums, Integer target,Integer left,Integer right) {if(left>right) return -1;int l=left;int r=right;int mid=(l+r)>>>1;if(nums[mid]>target){return binarysearch(nums,target,left,mid-1);}else if(nums[mid]<target){return binarysearch(nums,target,mid+1,right);}
return mid;}2)在一个有序数组中,找 >= 某个数最左侧的位置
/**Integer[] nums2={1,1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,4,5,5,5};System.out.println(binarysearch2(nums2, 3, 0, nums2.length - 1));
**/
private static int binarysearch2(Integer[] nums, Integer target,Integer left,Integer right) {if(left>right) return -1;int l=left;int r=right;int t=0;while(l<=r){int mid=(l+r)>>>1;if(nums[mid]>=target){/*** 找到了一个 >= target的数,将位置记录下来,* 不过也可能在这个数的左边还存在 >= target 的数,* 所以就更新右边界,去左边继续寻找*/t=mid;r=mid-1;}else{//这里就是 nums[mid]的值比target要小,更新左边界,继续去数组右边去找l=mid+1;}}
return t;}
//输出:103)局部最小值问题 (数组无序,相邻的两个数不相等 局部最小定义:arr[0] < arr[1] 数组0位置的值就是局部最小,arr[arr.length-1] < arr[arr.length-2] 数组最后一个位置的值就是局部最小,对于数组其他位置上的数 ,满足 arr[i-1] > arr[i] < arr[i+1] i位置上的数就是局部最小)
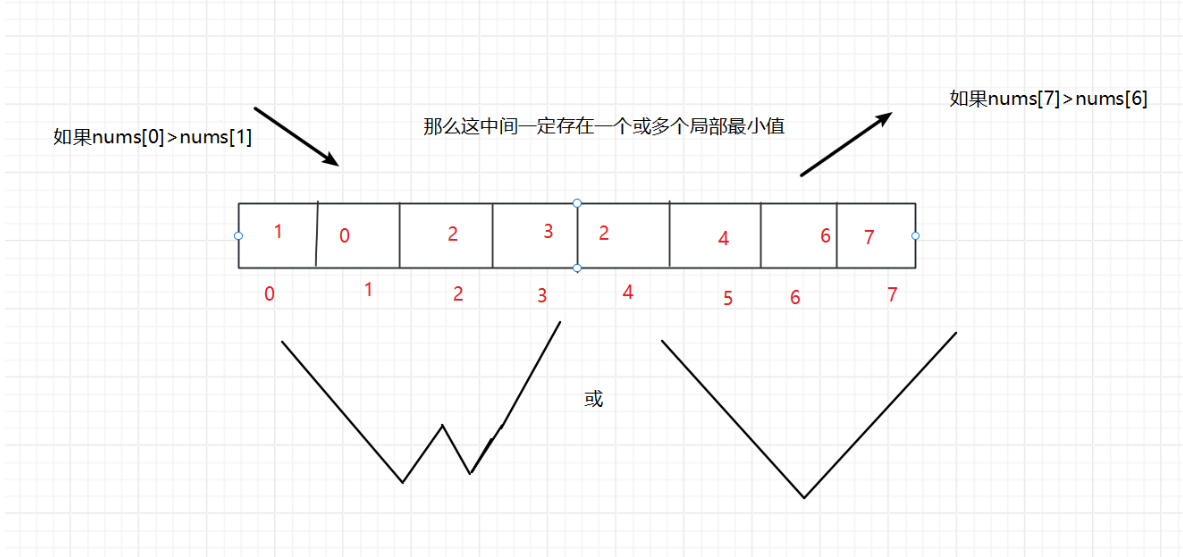
/**Integer[] nums3={1,0,1,3,6,5,1,2,3};System.out.println(binarysearch3(nums3));
**/
private static int binarysearch3(Integer[] nums) {int l=0;int r=nums.length-1;if(nums[l]<nums[l+1]) return l;if(nums[r]<nums[r-1]) return r;//如果执行到了这里,表示数组的两个边界都不是局部最小值,那么在这数组之中,一定存在一个局部最小值while(l<=r){int mid=(l+r)>>>1;if(nums[mid]<nums[mid-1] && nums[mid]<nums[mid]+1){return mid;}if(nums[mid]>nums[mid-1]){r=mid-1;} else if (nums[mid]>nums[mid+1]) {l=mid+1;}}return -1;}
//输出: 1对数器
有一个你想要测的方法 a,
实现复杂度不好但是容易实现的方法 b ,
实现一个随机样本产生器,
把方法 a 和方法 b 跑相同的随机样本,看看得到的结果是否一样。
如果有一个随机样本是的对比结果不一致,打印样本进行人工干预,改对方法 a 或 方法 b
当样本数量很多时对比测试是否依然正确,如果依然正确,就可以确定方法 a 已经正确
这里以插入排序作为方法a,java中本身提供的sort方法作为方法b
public static void main(String[] args) {int testTime=500000;int maxSize=100;int maxValue=100;boolean succeed=true;for(int i=0;i<testTime;i++){int[] arr1=generateRandomArray(maxSize,maxValue);int[] arr2=copyArray(arr1);//对arr1数组深拷贝MySort(arr1);//插入排序 a方法comparator(arr2);//b方法if(!isEqual(arr1,arr2)){//如果排序后的两个方法中的值存在差异succeed=false;break;}}System.out.println(succeed ? "Nice":"Fucking fucked");
int[] array = generateRandomArray(maxSize, maxValue);System.out.println(Arrays.toString(array));MySort(array);System.out.println(Arrays.toString(array));
}
//随机生成一个长度位maxSize,最大值为maxValue的int类型的数组public static int[] generateRandomArray(int maxSize,int maxValue){/*** Math.random() -> [0,1) 所有的小数,等概率返回一个 因为在计算机中,数的位数是有限制的,所以可以确定所有的小数,在数学上就不行。* Math.random()*N -> [0,N) 所有的小数,等概率返回一个* (int)(Math.random()*N) -> [0,N-1] 所有的整数,等概率返回一个*/
int[] arr=new int[(int)((maxSize+1)*Math.random())];//长度随机for(int i=0;i<arr.length;i++){arr[i]=(int) ((maxValue+1)*Math.random())-(int)(maxValue*Math.random());}return arr;}
//深拷贝
private static int[] copyArray(int[] arr1) {if(arr1==null) return null;int[] arr=new int[arr1.length];for (int i = 0; i < arr1.length; i++) {arr[i]=arr1[i];}return arr;}
//插入排序
private static void MySort(int[] nums) {if(nums==null || nums.length<2){return;}int l=nums.length;for(int i=1;i<l;i++){for(int j=i;j>0;j--){if(nums[j]<nums[j-1]){swap(nums,j,j-1);}else{break;}}}}
//交换
private static void swap(int[] nums, int i, int j) {int tmp= nums[i];nums[i]= nums[j];nums[j]=tmp;}
//java提供的方法
private static void comparator(int[] arr2) {Arrays.sort(arr2);}
//比较两个数组中的内容是否完全一致
public static boolean isEqual(int[] arr1,int[] arr2){for (int i = 0; i < arr1.length; i++) {if(arr1[i]!=arr2[i]) return false;}return true;}
## 比较器
返回负数的时候,认为第一个参数排在前面 -----> 升序
返回正数的时候,认为第二个参数排在前面 -----> 降序
返回0的时候,谁排在前面无所谓
PriorityQueue<Integer> heap = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o1-o2;}});递归
递归求数组中的最大值
剖析递归行为何递归行为时间复杂度的估算
用递归方法找一个数组中的最大值,系统上到底是怎么做的
master公式的使用
T(N) = a*T(N/b) + O(N^d)
1)log(b,a) > d --> 时间复杂度为:O(N^log(b,a))
2)log(b,a) = d --> 时间复杂度为:O(N^d * logN)
3)log(b,a) < d --> 时间复杂度为:O(N^d)
递归求数组中的最大值
public static int findMax(int[] arr,int left,int right){if(left==right){return arr[left];}int mid=left+((right-left)>>1);int leftMax=findMax(arr,left,mid);int rightMax=findMax(arr,mid+1,right);return Math.max(leftMax,rightMax);}执行流程
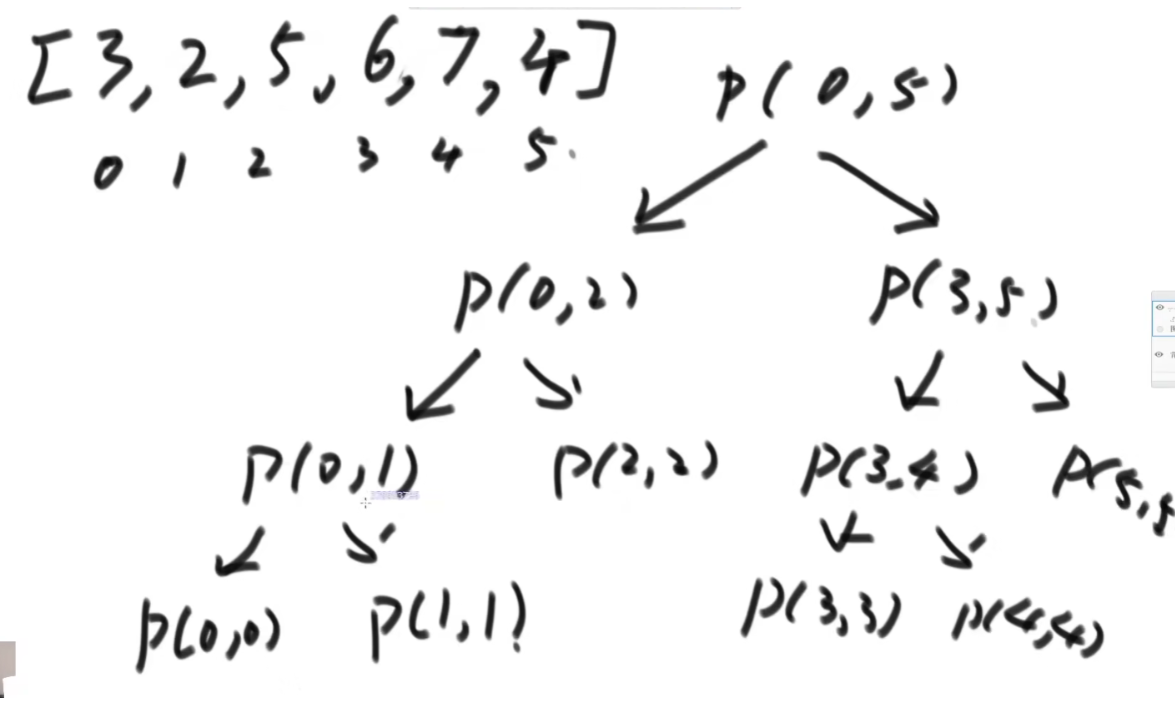
随着每一次findMax函数的调用,都会在java虚拟机栈中创建一个栈帧,等待每一个栈帧中的内容执行完毕后返回结果给上一层调用它的栈帧,这样一层层的调用,到最后,最开始的那一个栈帧对应的函数就可以得到最终的结果。
根据master公式,我们可以得出下面这个数据
T(N) = 2T(N/2)+O(1)a=2,b=2,d=0a=2因为一个函数中包含了两次子函数的调用b=2因为调用一次子函数的数据是父函数的一半d=0因为除了调用子函数之外的代码的时间复杂度是常数项所以 log(a,b)>d所以T(N)=T(N^log(1,1))=T(N),跟直接循环得到数组中的最大值的时间复杂度结果一样堆
堆结构
堆结构就是用数组实现的完全二叉树结构,完全二叉树是一种特殊的二叉树,其中除了最后一层外,每一层的节点都被完全填满,并且最后一层的节点都靠左对齐。
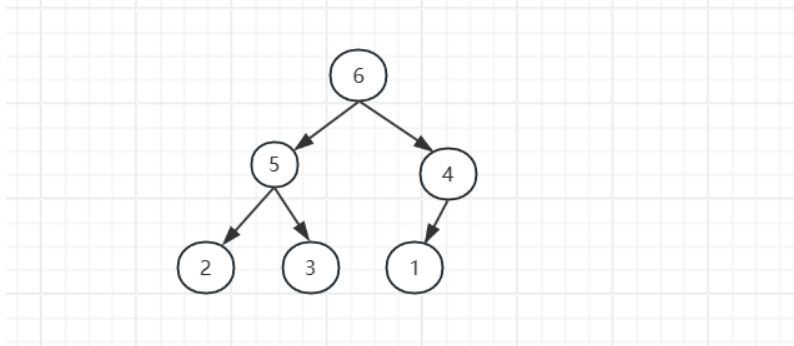
完全二叉树中如果每颗子树的最大值都在顶部就是大根堆
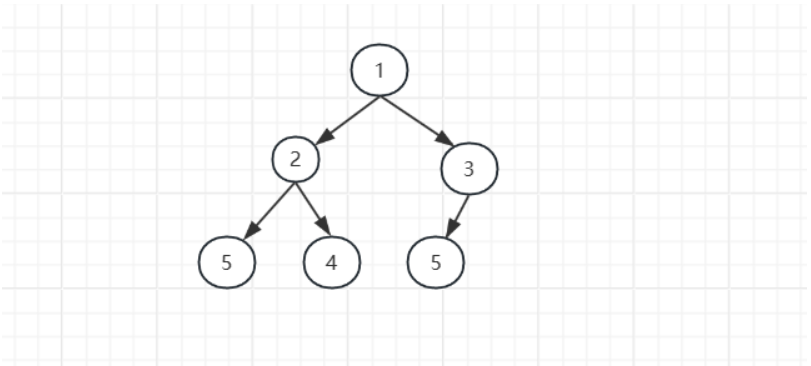
完全二叉树中如果每颗子树的最小值都在顶部就是小根堆
堆结构的heapInsert与heapify操作
/*** index上的值满足大根堆的条件从下往上移动* @param arr 数组* @param index 要移动的元素* 时间复杂度取决于树的高度:O(logN)*/public static void heapInsert(int[] arr,int index){//index和index的父节点进行比较,如果arr[index]>arr[(index-1)/2],说明它比父节点的值要大,就交换这父子元素的位置。否则,while循环结束//当index=0的时候,(index-1)/2 =0,此时的条件不满足,while循环就结束while(arr[index]>arr[(index-1)/2]){swap(arr,index,(index-1)/2);index=(index-1)/2;}}
/*** index上的值满足大根堆的条件从上往下移动* @param arr 数组* @param index 要移动的元素* @param heapSize 堆的大小* 时间复杂度取决于树的高度:O(logN)*/public static void heapify(int[] arr,int index,int heapSize){//当前节点的左孩子节点int left=2*index+1;//当左孩子节点存在的时候while (left<heapSize){//选择左孩子和右孩子中大的一个int largest=(left+1) < heapSize && arr[left+1]>arr[left]?(left+1):left;//选择父节点和孩子节点之间大的一个largest=arr[largest]>arr[index]?largest:index;//如果父节点是大的一个,说明已经满足大顶堆的条件,breakif(largest==index){break;}//交换父节点和孩子节点的值swap(arr,index,largest);//移动到交换后的孩子节点index=largest;//当前节点的左孩子节点left=index*2+1;}}堆结构的增大和减少:
堆结构的增大:将增加的值放到数组的最后一位,然后调用heapInsert函数
堆结构的减少:将要删除的元素所在位置记录为index,并且和最后一位互换,然后数组长度减1,调用Heapify函数
所以也可以说堆结构就是优先级队列结构。
在Java中封装了一个优先级队列PriorityQueue
PriorityQueue<Integer> heap = new PriorityQueue<>();PriorityQueue默认的就是使用小根堆实现的,也可以使用比较器自己定义。
如果在我们的需求中仅仅只是对堆中的数据进行add和poll的话,就可以使用PriorityQueue,这样的效率也比较高。
比如:
已知一个几乎有序的数组(几乎有序是指,如果把数组排好顺序的话,每个元素移动的距离不超过k,并且k相对于数组的长度来说比较小),请选择一个合适的排序算法针对这个数据进行排序。
代码:
/**
* int[] arr2={2,3,1,4,6,5};
* heapSortByK(arr2,2);
* System.out.println(Arrays.toString(arr2));
**/
public static void heapSortByK(int[] arr,int k){PriorityQueue<Integer> heap = new PriorityQueue<>();int index=0;/*** 先将数组中前k的元素加入到堆中,这前k的元素中,一定包含数组0位置上正确的数字,就是数字中的最小值*/for(;index<=Math.min(k,arr.length);index++){heap.add(arr[index]);}int i=0;/*** 每一次将数组中k位置后面的元素加入堆中,并弹出堆顶的位置,* 弹出的元素就是数字i位置上应该放的元素。*/for(;index<arr.length;index++){heap.add(arr[index]);arr[i++]=heap.poll();}while (!heap.isEmpty()){arr[i++]=heap.poll();}}运行结果:
[1, 2, 3, 4, 5, 6]不过如果我们的业务需要修改堆中的结构,比如删除或修改一个堆中的数据,那么使用PriorityQueue就不是一个最好的选择,因为PriorityQueue它不能确定我们所修改的位置,只能一个一个的遍历堆中的数据,判断这个数据是否需要进行heapify,这样PriorityQueue的效率就不高。如果我们有这样的需求,就需要我们自己手写堆,我们手写的堆在修改堆结构时可以知道是那里发生了修改,直接在修改的位置进行heapify即可。
相关文章:

算法学习(持续更新中)
学习视频:一周刷爆LeetCode,算法大神左神(左程云)耗时100天打造算法与数据结构基础到高级全家桶教程,直击BTAJ等一线大厂必问算法面试题真题详解(马士兵)_哔哩哔哩_bilibili 时间复杂度 一个操…...

蓝桥杯 2023 省B 飞机降落
首先,这题要求的数据量比较少,我们可以考虑考虑暴力解法。 这题可能难在很多情况的考虑,比如说: 现在时间是10,有个飞机20才到,我们是可以干等10分钟。 #include <iostream> #include <…...
基于python的变配电室运行状态评估与预警系统flask-django-nodejs-php
近年来,随着我国工业化、城镇化步伐的不断加快,城市配电网络取得令人瞩目的发展成果。变配电室是供配电系统的核心,在供配电系统中占有特殊的重要地位[1]。变配电室电气设备运行状态和环境信息缺乏必要的监测评估预警手段,如有一日遭遇突发情…...
,右键单击展示操作菜单,可编辑单元格高亮展示)
el-table左键双击单元格编辑内容(输入框输入计算公式可直接得出结果),右键单击展示操作菜单,可编辑单元格高亮展示
vue2点击左侧的树节点(el-tree)定位到对应右侧树形表格(el-table)的位置,树形表格懒加载 表格代码 <el-table ref"singleTable" :data"detailsList" highlight-current-row"" row-key"detailId"…...

实现HBase表和RDB表的转化(附Java源码资源)
实现HBase表和RDB表的转化 一、引入 转化为HBase表的三大来源:RDB Table、Client API、Files 如何构造通用性的代码模板实现向HBase表的转换,是一个值得考虑的问题。这篇文章着重讲解RDB表向HBase表的转换。 首先,我们需要分别构造rdb和hba…...

10:00面试,10:06就出来了,问的问题有点变态。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到8月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...

【Python】: Django Web开发实战(详细教程)
Python Django全面介绍 Django是一个非常强大的Python Web开发框架,它以"快速开发"和"干净、实用的设计"为设计宗旨。本文将从Django的基本概念开始,逐渐引导大家理解如何使用Django构建复杂的web应用程序。 Django基本概念与原理…...
)
突破编程_C++_C++11新特性(tuple)
1 std::tuple 简介 1.1 std::tuple 概述 std::tuple 是一个固定大小的不同类型值的集合,可以看作 std::pair 的泛化,即 std::pair 是 std::tuple 的一个特例,其长度受限为 2。与 C# 中的 tuple 类似,但 std::tuple 的功能更为强…...
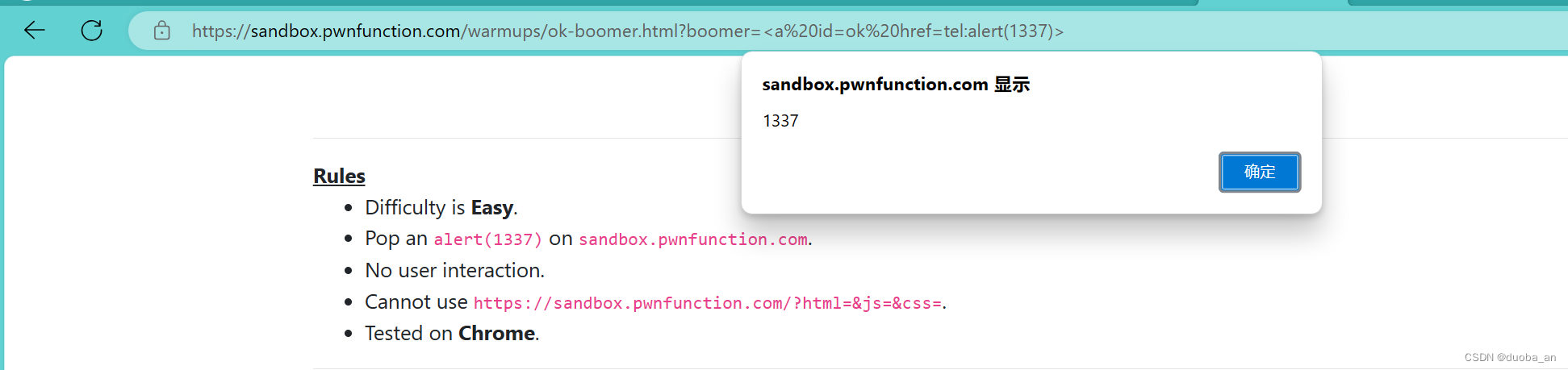
xss.pwnfunction(DOM型XSS)靶场
环境进入该网站 Challenges (pwnfunction.com) 第一关:Ma Spaghet! 源码: <!-- Challenge --> <h2 id"spaghet"></h2> <script>spaghet.innerHTML (new URL(location).searchParams.get(somebody) || "Somebo…...

安装 docker 和 jenkins
安装 docker #安装 软件包 docker yum install -y yum-utils device-mapper-persistent-data lvm2#设置 yum 源 yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo yum-config-manager --add-repo http://mirrors.aliyun.com/docker-c…...

jni入门学习 CMakeLists脚本
在 Android Studio 中使用 CMake 可以编译 C/C 代码,这为开发者提供了在 Android 应用中嵌入本地代码的能力。下面是关于在 Android Studio 中使用 CMake 编译的详细说明: 1. 创建 CMakeLists.txt 文件: 首先,你需要在项目的根目…...

如何在没有向量数据库的情况下使用知识图谱实现RAG
引言 传统上,为大型语言模型(LLMs)提供长期记忆通常涉及到使用检索增强生成(RAG)解决方案,其中向量数据库作为长期记忆的存储机制。然而,我们是否能在没有向量数据库的情况下达到相同效果呢&am…...
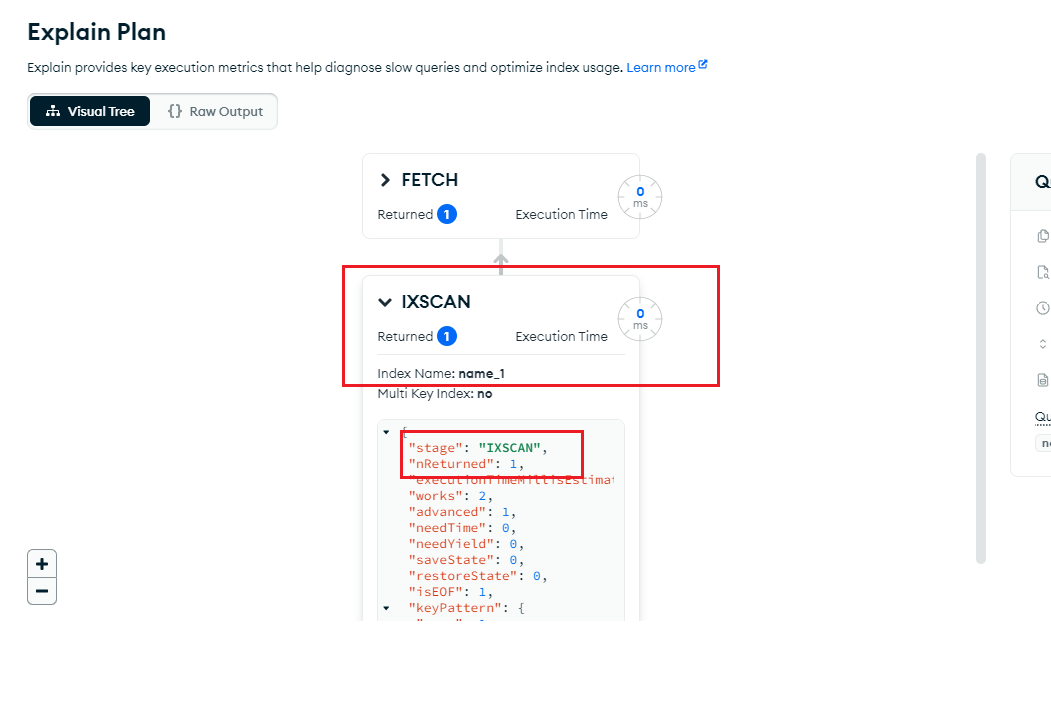
6.如何判断数据库搜索是否走索引?
判断是否使用索引搜索 索引在数据库中是一个不可或缺的存在,想让你的查询结果快准狠,还是需要索引的来帮忙,那么在mongo中如何判断搜索是不是走索引呢?通常使用执行计划(解释计划、Explain Plan)来查看查询…...

Java并发编程的性能优化方案中,哪些方法比较常用
在Java并发编程的性能优化方案中,以下是一些常用的方法: 线程池的使用: 线程池可以复用线程,避免频繁地创建和销毁线程,从而提高系统性能。常用的线程池有FixedThreadPool、CachedThreadPool等。根据任务特性选择合适…...
)
AcWing 2867. 回文日期(每日一题)
原题链接:2867. 回文日期 - AcWing题库 2020 年春节期间,有一个特殊的日期引起了大家的注意:2020 年 2 月 2 日。 因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202,恰好是一个回文数。 我们称这样的日期是…...
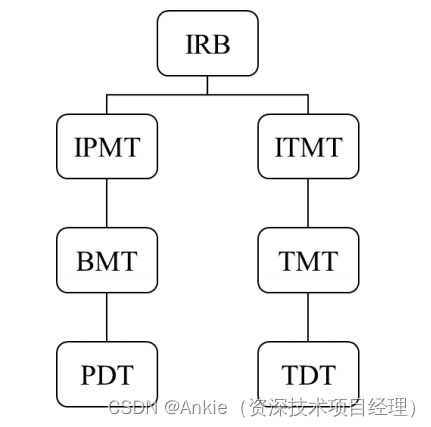
学习笔记-华为IPD转型2020:3,IPD的实施
3. IPD的实施 1999 年开始的 IPD 转型是计划中的多个转型项目中的第一个(Liu,2015)。华为为此次转型成立了一个专门的团队,从大约20人开始,他们是华为第一产业的高层领导。董事会主席孙雅芳是这个团队的负责人。该团…...
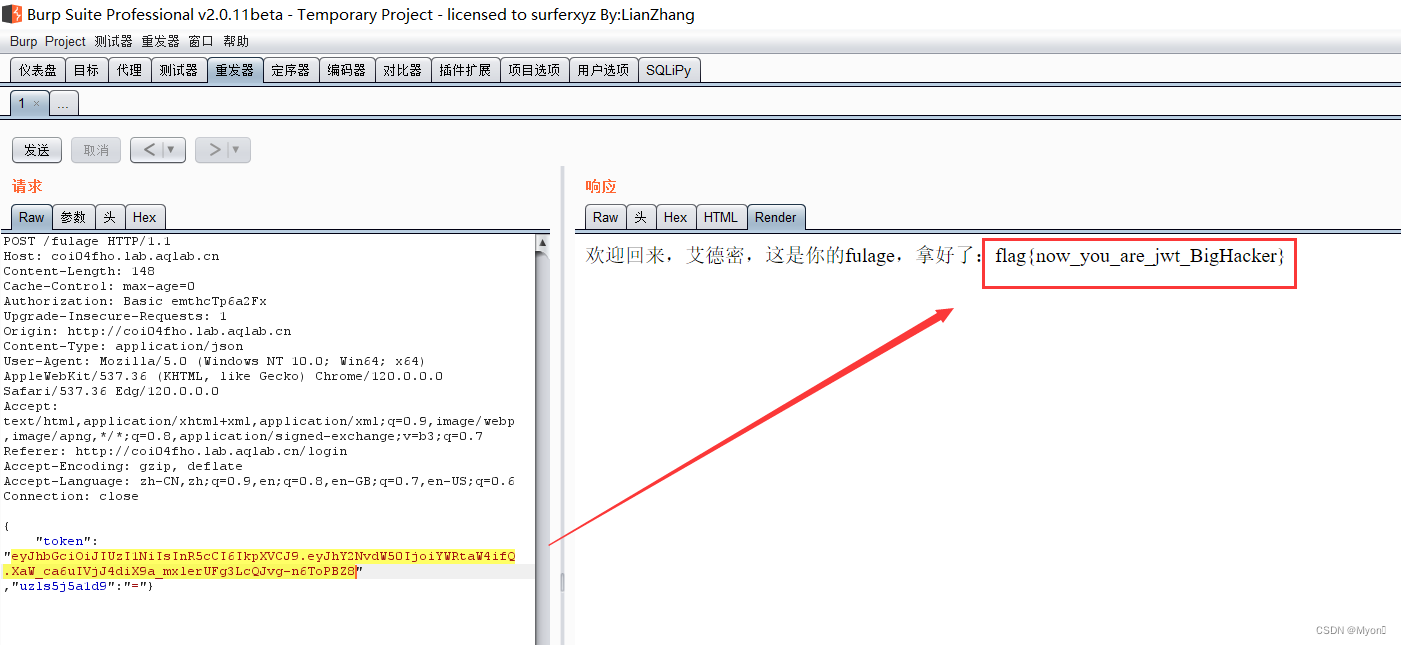
2024腾龙杯web签到题-初识jwt(签到:这是一个登录页面)
什么是 jwt? 它是 JSON Web Token 的缩写,是一个开放标准,定义了一种紧凑的、自包含的方式,用于作为JSON对象在各方之间安全地传输信息,该信息可以被验证和信任,因为它是数字签名的。它就是一种认证机制,…...
Monaco Editor系列(一)启动项目与入门示例解析
前言:作为一名程序员,我们工作中的每一天都在与代码编辑器打交道,相信各位前端程序员对 VS Code 一定都不陌生,VS Code 可以为我们提供代码高亮、代码对比等等功能,让我们在开发的时候,不需要对着暗淡无光的…...

DNA存储技术原理是什么?
随着大数据和人工智能的发展,全球每天产生的数据量剧增,对存储设备的需求也随之增长,数据存储问题日益凸显。传统的硬盘驱动器(HDD)、磁带等冷存和深度归档存储占据数据中心存储的60-70%,由于它们的访问频率…...

多维时序 | Matlab实现VMD-CNN-GRU变分模态分解结合卷积神经网络门控循环单元多变量时间序列预测
多维时序 | Matlab实现VMD-CNN-GRU变分模态分解结合卷积神经网络门控循环单元多变量时间序列预测 目录 多维时序 | Matlab实现VMD-CNN-GRU变分模态分解结合卷积神经网络门控循环单元多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现VMD-CN…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
