微分学<6>——Taylor公式
索引
- Taylor公式
- Taylor公式的定性分析
- 定理6.1 Taylor公式(Peano余项)
- Taylor公式的定量分析
- 定理6.2 Taylor公式(Lagrange余项)
Taylor公式
Taylor公式的定性分析
定理6.1 Taylor公式(Peano余项)
若函数 f ( x ) f\left ( x \right ) f(x)在 x 0 x_{0} x0处的 n n n阶导数均存在,则存在邻域 U ( x 0 , δ ) U\left ( x_{0},\delta \right ) U(x0,δ)使得 f ( x ) f\left ( x \right ) f(x)满足以下公式:
f ( x ) = ∑ k = 0 n f ( k ) ( x 0 ) ( x − x 0 ) k k ! + r n ( x ) f\left ( x \right ) =\sum_{k=0}^{n}\frac{f^{\left ( k \right ) } \left ( x_{0} \right )\left ( x-x_{0} \right )^{k} }{k!}+r_{n} \left ( x \right ) f(x)=∑k=0nk!f(k)(x0)(x−x0)k+rn(x)
其中Peano余项 r n ( x ) = o ( ( x − x 0 ) n ) ( x → x 0 ) r_{n} \left ( x \right )=o \left ( \left ( x-x_{0} \right )^{n} \right )(x\to x_{0} ) rn(x)=o((x−x0)n)(x→x0),代表 f ( x ) f\left ( x \right ) f(x)在Taylor近似时产生的误差,余下的 n n n次多项式记为 P n ( x ) P_{n}\left ( x \right ) Pn(x),即 x 0 x_{0} x0处的 n n n次Taylor多项式。
r n ( x ) = f ( x ) − P n ( x ) = f ( x ) − ∑ k = 0 n f ( k ) ( x 0 ) ( x − x 0 ) k k ! r_{n}\left ( x \right ) =f\left ( x \right ) -P_{n}\left ( x \right ) =f\left ( x \right ) -\sum_{k=0}^{n}\frac{f^{\left ( k \right ) } \left ( x_{0} \right )\left ( x-x_{0} \right )^{k} }{k!} rn(x)=f(x)−Pn(x)=f(x)−∑k=0nk!f(k)(x0)(x−x0)k,
r n ( n − 1 ) ( x ) = f ( n − 1 ) ( x ) − ∑ k = n − 1 n f ( k ) ( x 0 ) ( x − x 0 ) ( k − ( n − 1 ) ) ( k − ( n − 1 ) ) ! = f ( n − 1 ) ( x ) − ( f ( n − 1 ) ( x 0 ) 0 ! + f ( n ) ( x 0 ) ( x − x 0 ) 1 ! ) = f ( n − 1 ) ( x ) − f ( n − 1 ) ( x 0 ) − f ( n ) ( x 0 ) ( x − x 0 ) \begin{array}{l} &r^{\left(n-1\right)} _{n}\left ( x \right ) \\ =&f^{\left ( n-1 \right ) }\left ( x \right ) -\sum _{k=n-1}^{n}\frac{f^{\left ( k \right ) }\left ( x_{0} \right ) \left ( x-x_{0} \right )^{\left ( k-\left ( n-1 \right ) \right ) } }{\left ( k-\left (n-1 \right ) \right ) !} \\ =&f^{\left ( n-1 \right ) }\left ( x \right )-\left ( \frac{f^{\left ( n-1 \right ) }\left ( x_{0} \right ) }{0!}+\frac{f^{\left ( n \right )}\left ( x_{0} \right )\left ( x-x_{0} \right ) }{1!}\right ) \\ =&f^{\left ( n-1 \right ) }\left ( x \right )-f^{\left ( n-1 \right ) }\left ( x_{0} \right )-f^{\left ( n \right )}\left ( x_{0} \right )\left ( x-x_{0} \right ) \end{array} ===rn(n−1)(x)f(n−1)(x)−∑k=n−1n(k−(n−1))!f(k)(x0)(x−x0)(k−(n−1))f(n−1)(x)−(0!f(n−1)(x0)+1!f(n)(x0)(x−x0))f(n−1)(x)−f(n−1)(x0)−f(n)(x0)(x−x0),
因为函数 f ( x ) f\left ( x \right ) f(x)在 x 0 x_{0} x0处的 n n n阶导数均存在,所以 f ( x ) f\left ( x \right ) f(x)的前 n − 1 n-1 n−1阶导函数一定连续且可导。
连续引用n-1次L’Hospital法则, lim x → x 0 r n ( x ) ( x − x 0 ) n = lim x → x 0 r n ( 1 ) ( x ) n ( x − x 0 ) n − 1 = ⋯ = lim x → x 0 r n ( n − 1 ) ( x ) n ! ( x − x 0 ) \lim _{x\to x_{0} } \frac{r_{n}\left ( x \right ) }{\left ( x-x_{0} \right )^{n} }= \lim _{x\to x_{0} }\frac{r^{\left ( 1 \right ) } _{n}\left ( x \right ) }{n\left ( x-x_{0} \right )^{n-1} }=\cdots =\lim _{x\to x_{0} }\frac{r^{\left ( n-1 \right ) } _{n}\left ( x \right ) }{n! \left ( x-x_{0} \right ) } limx→x0(x−x0)nrn(x)=limx→x0n(x−x0)n−1rn(1)(x)=⋯=limx→x0n!(x−x0)rn(n−1)(x),
展开 r n ( n − 1 ) ( x ) r^{\left ( n-1 \right ) } _{n}\left ( x \right ) rn(n−1)(x), lim x → x 0 r n ( n − 1 ) ( x ) n ! ( x − x 0 ) = 1 n ! lim x → x 0 ( f ( n − 1 ) ( x ) − f ( n − 1 ) ( x 0 ) x − x 0 − f ( n ) ( x 0 ) ) \lim _{x\to x_{0} }\frac{r^{\left ( n-1 \right ) } _{n}\left ( x \right ) }{n! \left ( x-x_{0} \right ) }=\frac{1}{n!}\lim _{x\to x_{0} } \left ( \frac{f^{\left ( n-1 \right ) }\left ( x \right ) -f^{\left ( n-1 \right ) }\left ( x_{0} \right ) }{x-x_{0} } -f^{\left ( n \right ) }\left ( x_{0} \right ) \right ) limx→x0n!(x−x0)rn(n−1)(x)=n!1limx→x0(x−x0f(n−1)(x)−f(n−1)(x0)−f(n)(x0)),
根据高阶导数定义, lim x → x 0 f ( n − 1 ) ( x ) − f ( n − 1 ) ( x 0 ) x − x 0 = f ( n ) ( x 0 ) \lim _{x\to x_{0} }\frac{f^{\left ( n-1 \right ) }\left ( x \right ) -f^{\left ( n-1 \right ) }\left ( x_{0} \right ) }{x-x_{0} }=f^{\left ( n \right ) }\left ( x_{0} \right ) limx→x0x−x0f(n−1)(x)−f(n−1)(x0)=f(n)(x0),
所以 lim x → x 0 r n ( x ) ( x − x 0 ) n = lim x → x 0 r n ( n − 1 ) ( x ) n ! ( x − x 0 ) = 0 \lim _{x\to x_{0} } \frac{r_{n}\left ( x \right ) }{\left ( x-x_{0} \right )^{n} }=\lim _{x\to x_{0} }\frac{r^{\left ( n-1 \right ) } _{n}\left ( x \right ) }{n! \left ( x-x_{0} \right ) }=0 limx→x0(x−x0)nrn(x)=limx→x0n!(x−x0)rn(n−1)(x)=0, r n ( x ) = o ( ( x − x 0 ) n ) ( x → x 0 ) r_{n} \left ( x \right )=o \left ( \left ( x-x_{0} \right )^{n} \right )(x\to x_{0} ) rn(x)=o((x−x0)n)(x→x0)。
Taylor公式的定量分析
定理6.2 Taylor公式(Lagrange余项)
函数 f ( x ) f\left ( x \right ) f(x)在闭区间 [ a , b ] \left [ a,b \right ] [a,b]上存在 n n n阶连续导数,在开区间 ( a , b ) \left ( a,b \right ) (a,b)上存在 n + 1 n+1 n+1阶导数,取一定点 x 0 ∈ [ a , b ] x_{0}\in \left [ a,b \right ] x0∈[a,b],则 ∀ x ∈ [ a , b ] \forall x\in \left [ a,b \right ] ∀x∈[a,b], f ( x ) = ∑ k = 0 n f ( k ) ( x 0 ) ( x − x 0 ) k k ! + r n ( x ) f\left ( x \right )=\sum_{k=0}^{n}\frac{f^{\left ( k \right ) }\left ( x_{0} \right )\left ( x-x_{0} \right )^{k} }{k!}+r_{n}\left ( x \right ) f(x)=∑k=0nk!f(k)(x0)(x−x0)k+rn(x),其中Lagrange余项 r n ( x ) = f ( n + 1 ) ( ξ ) ( x − x 0 ) n + 1 ( n + 1 ) ! r_{n}\left ( x \right )=\frac{f^{\left ( n+1 \right ) }\left ( \xi \right )\left ( x-x_{0} \right )^{n+1} }{\left ( n+1 \right ) !} rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1,其中 ξ \xi ξ位于 x x x和 x 0 x_{0} x0之间。
当 n = 0 n=0 n=0时,Taylor公式表现为Lagrange中值定理的形式。
构造函数 G ( t ) = f ( x ) − ∑ k = 0 n ( f ( k ) ( t ) k ! ( x − t ) k ) G\left ( t \right )=f\left ( x \right )-\sum_{k=0}^{n}\left ( \frac{f^{\left ( k \right ) }\left (t \right ) }{k!}\left ( x-t \right )^{k} \right) G(t)=f(x)−∑k=0n(k!f(k)(t)(x−t)k)和 H ( t ) = ( x − t ) n + 1 H\left ( t \right )=\left ( x-t \right )^{n+1} H(t)=(x−t)n+1,
不妨设 x < x 0 x<x_{0} x<x0,
G ( x ) = f ( x ) − ∑ k = 1 n ( f ( k ) ( t ) k ! ( x − x ) k ) − f ( t ) 0 ! ( x − t ) 0 = f ( x ) − f ( x ) = 0 G\left ( x \right )=f\left ( x \right )-\sum_{k=1}^{n}\left ( \frac{f^{\left ( k \right ) }\left (t \right ) }{k!}\left ( x-x \right )^{k} \right)-\frac{f\left ( t \right ) }{0!}\left ( x-t \right )^{0}=f\left ( x \right )-f\left ( x \right )=0 G(x)=f(x)−∑k=1n(k!f(k)(t)(x−x)k)−0!f(t)(x−t)0=f(x)−f(x)=0;
G ( x 0 ) = f ( x ) − ∑ k = 0 n ( f ( k ) ( x 0 ) k ! ( x − x 0 ) k ) G\left ( x_{0} \right )=f\left ( x \right )-\sum_{k=0}^{n}\left ( \frac{f^{\left ( k \right ) }\left (x_{0} \right ) }{k!}\left ( x-x_{0} \right )^{k} \right) G(x0)=f(x)−∑k=0n(k!f(k)(x0)(x−x0)k);
H ( x ) = ( x − x ) n + 1 = 0 H\left ( x \right )=\left ( x-x \right )^{n+1}=0 H(x)=(x−x)n+1=0;
H ( x 0 ) = ( x − x 0 ) n + 1 H\left ( x_{0} \right )=\left ( x-x_{0} \right )^{n+1} H(x0)=(x−x0)n+1;
G ′ ( t ) = − ∑ k = 0 n ( f ( k ) ( t ) ( x − t ) k k ! ) ′ = ∑ k = 1 n f ( k ) ( t ) ( x − t ) k − 1 ( k − 1 ) ! − ∑ k = 1 n + 1 f ( k ) ( t ) ( x − t ) ( k − 1 ) ( k − 1 ) ! = − f ( n + 1 ) ( t ) ( x − t ) n n ! \begin{array}{l} &G^{\prime } \left ( t \right ) \\ =&-\sum_{k=0}^{n}\left ( \frac{f^{\left ( k \right ) }\left (t \right )\left ( x-t \right )^{k}}{k!} \right)^{\prime } \\ =&\sum_{k=1}^{n}\frac{f^{\left ( k \right ) }\left ( t \right )\left ( x-t \right )^{k-1} }{\left ( k-1 \right ) !}- \sum_{k=1}^{n+1} \frac{f^{\left ( k \right ) }\left ( t \right )\left ( x-t \right )^{\left ( k-1 \right )} }{\left ( k-1 \right )!}\\ =&-\frac{f^{\left ( n+1 \right ) }\left ( t \right )\left ( x-t \right )^{n} }{n!} \end{array} \\ ===G′(t)−∑k=0n(k!f(k)(t)(x−t)k)′∑k=1n(k−1)!f(k)(t)(x−t)k−1−∑k=1n+1(k−1)!f(k)(t)(x−t)(k−1)−n!f(n+1)(t)(x−t)n
H ′ ( t ) = − ( n + 1 ) ( x − t ) n H^{\prime } \left ( t \right ) =-\left ( n+1 \right )\left ( x-t \right )^{n} H′(t)=−(n+1)(x−t)n;
引用Cauchy中值定理, ∃ ξ ∈ ( x , x 0 ) \exists \xi \in \left ( x ,x_{0} \right ) ∃ξ∈(x,x0), r n ( x ) ( x − x 0 ) n + 1 = G ( x 0 ) H ( x 0 ) = G ( x 0 ) − G ( x ) H ( x 0 ) − H ( x ) = G ′ ( ξ ) H ′ ( ξ ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ⇒ r n ( x ) = f ( n + 1 ) ( ξ ) ( x − x 0 ) n + 1 ( n + 1 ) ! \frac{r_{n}\left ( x \right ) }{\left ( x-x_{0} \right )^{n+1} } =\frac{G\left ( x_{0} \right ) }{H\left ( x_{0} \right ) }=\frac{G\left ( x_{0} \right )-G\left ( x \right ) }{H\left ( x_{0} \right )-H\left ( x \right ) }=\frac{G^{\prime }\left ( \xi \right ) }{H^{\prime }\left ( \xi \right ) }=\frac{f^{\left ( n+1 \right ) }\left ( \xi \right )}{\left ( n+1 \right )! }\Rightarrow r_{n}\left ( x \right )=\frac{f^{\left ( n+1 \right ) }\left ( \xi \right )\left ( x-x_{0} \right )^{n+1} }{\left ( n+1 \right ) !} (x−x0)n+1rn(x)=H(x0)G(x0)=H(x0)−H(x)G(x0)−G(x)=H′(ξ)G′(ξ)=(n+1)!f(n+1)(ξ)⇒rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1。
相关文章:

微分学<6>——Taylor公式
索引 Taylor公式Taylor公式的定性分析定理6.1 Taylor公式(Peano余项) Taylor公式的定量分析定理6.2 Taylor公式(Lagrange余项) Taylor公式 Taylor公式的定性分析 定理6.1 Taylor公式(Peano余项) 若函数 f ( x ) f\left ( x \right ) f(x)在 x 0 x_{0} x0处的 n n n阶导数均…...
检索增强生成(RAG)应用的构建:LangChain与LlamaIndex的比较与选择
对于我要做RAG应用,我应该使用两者中的哪一个。或者说还是都使用? 在人工智能领域,检索增强生成(RAG)应用正变得越来越受欢迎,因为它们能够结合大型语言模型(LLMs)的自然语言处理能力…...
免费PDF转换和编辑工具 PDFgear 2.1.4
PDFgear是一款功能强大的 PDF 阅读及转换软件。 它支持多种文件格式的转换和编辑,同时还提供了丰富的功能模块,如签名、表单填写等,方便用户进行多样化的操作。 该软件界面简洁美观,操作简单易懂,适合不同层次的用户…...

uniapp,导航栏(切换项)有多项,溢出采取左滑右滑的形式展示
一、实现效果 当有多项的导航,或者说切换项,超出页面的宽度,我们采取可滑动的方式比较好一些!并且在页面右边加个遮罩,模拟最右边有渐变效果! 二、实现代码 html代码: <!-- 头部导航栏 --…...

计算机网络面经-什么是IPv4和IPv6?
前言 Internet协议(IP)是为连接到Internet网络的每个设备分配的数字地址。它类似于电话号码,是一种独特的数字组合,允许用户与他人通信。IP地址主要有两个主要功能。首先,有了IP,用户能够在Internet上被识别…...

彻底讲透:如何写sql能够有效的使用到复合索引?
在MySQL中,有效的使用复合索引需要确保查询条件按照索引定义的列顺序进行。以下是一个具体的例子: 假设我们有一个sales表,它有四个字段:customer_id、product_category、sale_date和amount。为了优化包含这些字段查询的性能&…...
?)
在Spring Boot中如何处理跨域请求(CORS)?
什么是跨域? 跨域(Cross-Origin Resource Sharing,CORS)是一种机制,它允许在 Web 页面上运行的脚本能够请求从不同源(域名、协议或端口)的资源。在浏览器安全策略中,有一条称为同源…...

好就业三种专业#信息安全#云计算#网络工程
一、信息安全专业 根据2021年网络安全宣传周白皮书的观察结果,网络安全产业对于人才的需求正以高速增长的趋势呈现,当前网络安全行业存在着巨大的人才缺口,平均供求比例约为1:2。这一现象导致了资深人才的储备不足,并且新人才的培…...

electron-builder打包
打包配置: "build": {"appId": "cc11001100.electron.example-001", // 程序包名"copyright": "CC11001100", // 版权相关信息"productName": "example-001", // 安装包文件名"direct…...

SQLiteC/C++接口详细介绍sqlite3_stmt类(四)
返回:SQLite—系列文章目录 上一篇:SQLiteC/C接口详细介绍sqlite3_stmt类(三) 下一篇:SQLiteC/C接口详细介绍sqlite3_stmt类(五) 7. sqlite3_bind_parameter_count函数 sqlite3_bind_param…...

微信小程序自定义组件
微信小程序中的自定义组件是指在微信小程序中创建的可重用的、可复用的组件,它可以被多个页面使用。自定义组件可以帮助我们提高开发效率,提高代码的可维护性和可重用性。以下是微信小程序中自定义组件的使用方法: 一. 创建自定义组件 首先…...

python练习3
用户登录注册案例 while True: print("\t\t\t英雄商城登录界面\n") print("~*"*38) print("\t\t\t1.用户登录\n") print("\t\t\t2.用户注册\n") print("\t\t\t3.退出系统\n") print("~*"*38) choice input("…...

docker离线安装并修改存储目录
docker下载 根据cpu选择不同版本,正常x86就选x86_64 下载地址:https://download.docker.com/linux/static/stable/ docker安装 tar -zxvf arm-docker-25.0.4.tgz sudo cp docker/* /usr/bin/ rm -rf docker/* mkdir /etc/docker vi /etc/docker/daemo…...
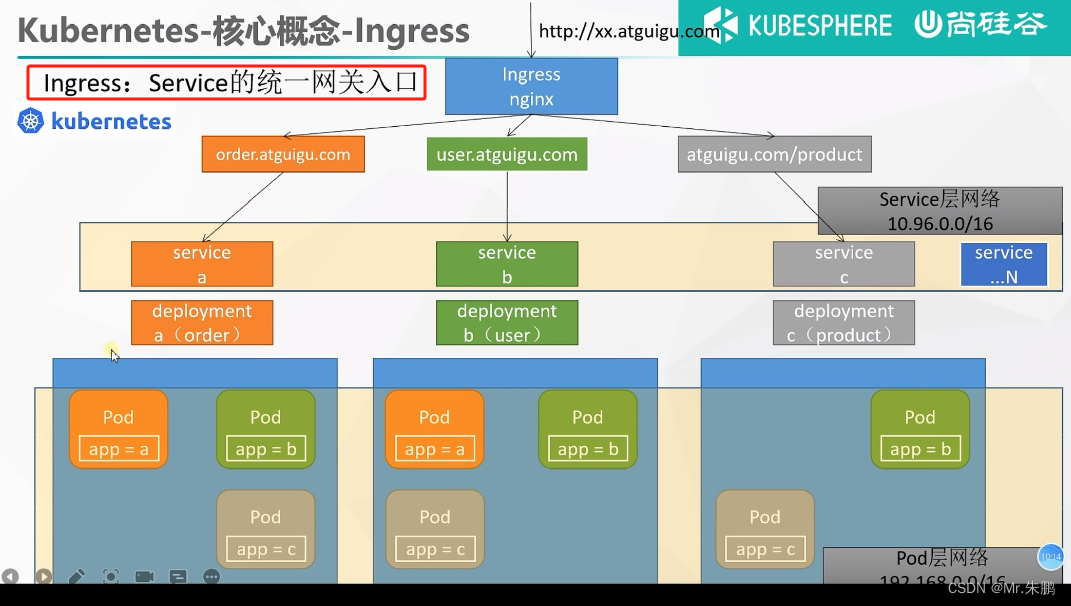
【云原生 • Kubernetes】认识 k8s、k8s 架构、核心实战
文章目录 Kubernetes基础概念1. 是什么2. 架构2.1 工作方式2.2 组件架构 3. k8s组件创建集群步骤一 基础环境步骤二 安装kubelet、kubeadm、kubectl步骤三 主节点使用kubeadm引导集群步骤四 副节点加入主节点步骤五 部署dashboard Kubernetes核心实战1. 资源创建方式2. Namespa…...

墨菲安全在软件供应链安全领域阶段性总结及思考
向外看:墨菲安全在软件供应链安全领域的一些洞察、思考、行动 洞察 现状&挑战: 过去开发安全体系是无法解决软件供应链安全问题的;一些过去专注开发安全领域的厂商正在错误的引导行业用开发安全思维解决软件供应链安全问题,治…...

智慧公厕:卫生、便捷、安全的新时代厕所变革
在城市快速发展的背景下,公共厕所的建设和管理变得越来越重要。智慧公厕作为厕所变革的一项全新举措,通过建立公共厕所全面感知监测系统,以物联网、互联网、大数据、云计算、自动化控制技术为支撑,实现对公共厕所的智能化管理和运…...
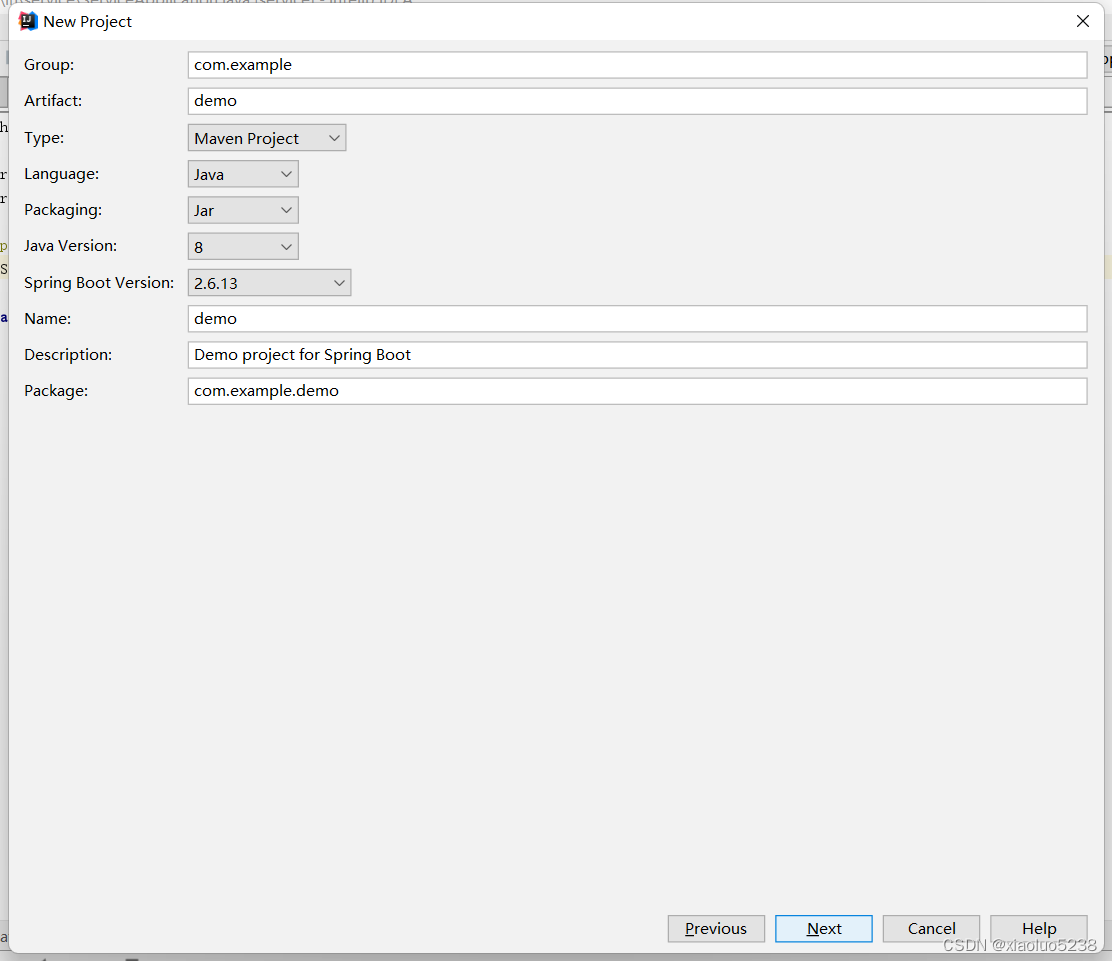
Idea 不能创建JDK1.8的spring boot项目
由于https://start.springboot.io/ 不支持JDK1.8,那么我们需要换idea的springboot创建源,需要换成 https://start.aliyun.com,这也是网上大部分教程说的,但是我这边会报这样的错误: Initialization failed for https:…...

【docker】Docker学习收集
写在前面 新公司开发使用docker来部署和统一大家的开发环境,故再次记录好用的学习链接和自己遇到的奇怪问题 实用链接 Docker教程详细 常用命令 个例问题 Q: docker在终端多开,A终端的修改会影响B吗 A: 会...

LoRa模块在野外科研与环境保护中的角色:科技守护自然之宝
随着科技的不断发展,LoRa(低功耗广域网)模块在野外科研与环境保护中正发挥着越来越重要的作用。其卓越的通信能力、低功耗特性以及良好的穿透能力,为科学家和环保人士提供了一种先进的技术手段,有助于更深入、更全面地…...

全国媒体公关服务资源分析,媒体邀约资源包括哪些?-51媒体网
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 全国媒体公关服务资源分析是一个涵盖多方面的复杂议题,主要涉及到不同媒体类型、传播渠道、以及公关策略等多个维度。在当前媒体环境下,媒体公关服务资源主要包括…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
