【力扣每日一题】lc1793. 好子数组的最大分数(单调栈)
LC1793. 好子数组的最大分数
题目描述
给你一个整数数组 nums (下标从 0 开始)和一个整数 k 。
一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i+1], ..., nums[j]) * (j - i + 1) 。
一个 好 子数组的两个端点下标需要满足 i <= k <= j 。
请你返回 好 子数组的最大可能 分数 。
1 <= nums.length <= 10^5
1 <= nums[i] <= 2 * 10^4
分析
数据要求非常高,n是1e5级别的,也就是O(n^3)、O(n^2)时间复杂度的算法都无法AC,所以正解只有O(n)或者O(n logn)的算法才能通过。本题正解是O(n)
暴力解法1:纯蛮力
三重循环,枚举i,再枚举j,再枚举i~j求出最小值
时间复杂度O(n^3)
for i in range(n):for j in range(i,n):mi = inffor k in range(i,j+1):mi = min(mi,nums[k])ans = max(ans,mi*(j-i+1))
这个暴力解法可以优化成O(n^2),就是先预处理出来mi[i][j],表示i~j的最小值。但是时间还是不满足题意
暴力解法2:贡献思维
枚举nums[i],找到当nums[i]是好子数组最小值时的最大区间。
即找到左边和右边离i最近的比它小的元素,就是边界,从而确定以nums[i]为最小值的子数组的范围。
时间复杂度O(n^2)
for i in range(n):# 找左边离i最近的比它小的元素j = iwhile j>=0 and nums[j]>=nums[i]:j -= 1l = j# 找右边离i最近的比它小的元素j = iwhile j<n and nums[j]>=nums[i]:j += 1r = jif l<k and r>k:res = (r-l-1)*nums[i]ans = max(ans,res)
正确解法
想一下暴力解法2有什么可以优化的地方呢?
其实在求左边(右边)离i最近的比它小的元素这个地方是O(n)的,其实可以用单调栈将这个操作优化成O(1)的。
为了解决这个问题,我们可以采用单调栈的方法来找到每个元素左边和右边第一个比它小的元素的位置。这是因为对于任意的元素nums[i],我们想要知道在其左边和右边第一个比它小的元素,从而确定以nums[i]为最小值的子数组的范围。
核心思路:枚举每一个Nums[i]作为最小值的好子数组的最大分数。
时间复杂度O(n)
AC 代码
class Solution:def maximumScore(self, nums: List[int], k: int) -> int:n = len(nums)# 单调栈,找到i左边/右边离他最近的比它小的数# l[i]表示nums[i]左边第一个比它小的元素的下标 l = [-1]*n# r[i]表示nums[i]右边第一个比它小的元素的下标 r = [n]*n# 使用单调栈计算l数组stk = []for i in range(n):while len(stk) and nums[stk[-1]] >= nums[i]:stk.pop()l[i] = stk[-1] if len(stk) else -1stk.append(i)stk = []for i in range(n-1,-1,-1):while len(stk) and nums[stk[-1]] >= nums[i]:stk.pop()r[i] = stk[-1] if len(stk) else nstk.append(i)ans = 0for i in range(n):if l[i]<k and r[i]>k:res = (r[i]-l[i]-1)*nums[i]ans = max(ans,res)return ans
相关文章:
)
【力扣每日一题】lc1793. 好子数组的最大分数(单调栈)
LC1793. 好子数组的最大分数 题目描述 给你一个整数数组 nums (下标从 0 开始)和一个整数 k 。 一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i1], ..., nums[j]) * (j - i 1) 。 一个 好 子数组的两个端点下标需要满足 i < k < j 。 请…...

ES的集群节点发现故障排除指南(1)
本文是ES官方文档关于集群节点发现与互联互通的问题排查指南内容。 英文原文(官网) 集群节点发现是首要任务 集群互连,重中之重! 在大多数情况下,发现和选举过程会迅速完成,并且主节点会长时间保持当选状…...

使用html+css制作一个发光立方体特效
使用htmlcss制作一个发光立方体特效 <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>Documen…...

贵州省二级分类土地利用数据(矢量)
贵州省,地处中国西南腹地,地貌属于中国西南部高原山地,境内地势西高东低,自中部向北、东、南三面倾斜,平均海拔在1100米左右。贵州高原山地居多,素有“八山一水一分田”之说。全省地貌可概括分为࿱…...
通过nginx+xray服务搭建及本地配置
一、xray服务配置 下载:https://github.com/XTLS/Xray-core 进入下载界面 这里我选择的是Xray-linux-64.zip 将文件解压到 /usr/local/xray 编辑配置文件/usr/local/xray/config.json uuid可以在v2ray客服端自动生成,也可以在UUID v4 生成器 - KKT…...
第一节 Axure RP产品经理原型进阶学习
第一天 1、认识RP9 Axure RP 9,Axure RP 9是美国 Axure Software Solution公司的旗舰产品, 是一个快速的原型工具,常用于各项网络设计,包括了原型图、线框图等等。 要进行原型设计,将文字性文档转变为互动性的可视画…...
 文件压缩)
Linux实战笔记(三) 文件压缩
大家好,我是半虹,这篇文章来讲 Linux 系统中常用的文件压缩方式 0、序言 在 Linux 系统中,存在许多打包或压缩文件的工具 这篇文章会对一些常用的工具进行分类整理和介绍 如果只是需要知道怎么对不同格式的文件做解压缩,可以直…...

树形递归模板
详情参考CSDN链接: https://www.cnblogs.com/lidar/p/12972792.html public class Menu {// 菜单idprivate String id;// 菜单名称private String name;// 父菜单idprivate String parentId;// 菜单urlprivate String url;// 菜单图标private String icon;// 菜单顺序private …...

Python实战:Pandas数据合并与重塑
本文将深入探讨Pandas库在数据合并与重塑方面的强大功能。我们将涵盖多种数据合并方法,如merge、join、concat等,以及数据重塑的技巧,如pivot_table、merge_asof等。 一、引言 Pandas是一个强大的Python数据分析库,它提供了丰富…...
如何理解 Linux 命令行参数与环境变量7
一、命令行参数 1.1参数介绍 在写C语言程序时,main函数是否可以带参数呢?------ 是可以的 int argc: 命令行参数的个数char *argv[ ]: 字符指针数组(指向各个命令行参数的字符指针所构成的数组) 我们写一段代码来打印一下看这…...

奥特曼回应GPT5
欢迎再次与大家会面!在积累了大量的信息和趋势后,今天我们将深入了解 Sora、OpenAI 董事会、以及近期与其有关的所有声讨。我们将直接跳入与 OpenAI 首席执行官 Sam Altman 的深度访谈,探讨从 AGI 到 GPT-5 的未来,以及 Sam 对人工…...
QT----给程序添加上任务栏托盘图标和退出
让我们的程序拥有任务栏托盘图标,实现程序后台运行,退出等功能 1、关闭程序保持后台 重写关闭事件,忽略点击窗口关闭 void MainWindow::closeEvent(QCloseEvent *event) {// 隐藏窗口,而不是真正关闭setVisible(false);// 忽略关闭事件&am…...

arm地址对齐的总结
static void axi_azx_writeb(u8 value, u8 __iomem *addr) { u32 data; u32 offset; offset (u64)addr & 0x03; // 编译器不允许地址做& 操作时要强转为数据 addr (u8 __iomem *)((u64)addr & 0xFFFFFFFFFFFFFFFC); // __iomem是个64位的地址 u8表示从这个地址…...
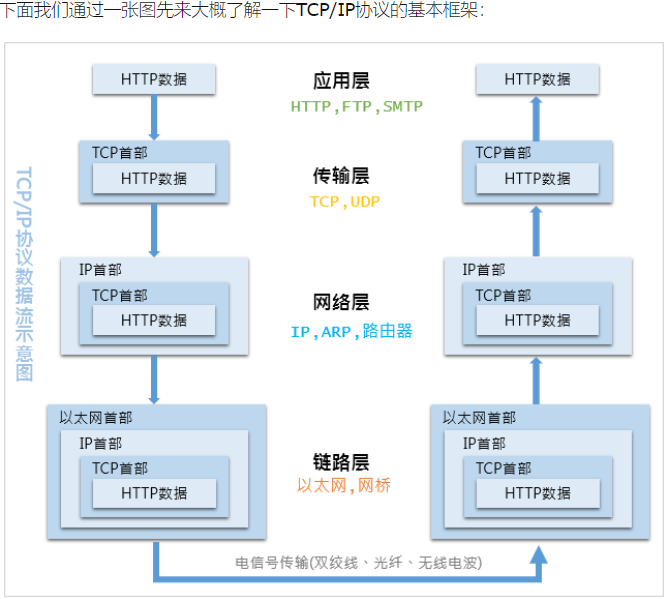
就业班 2401--3.13 走进网络
走进网络 长风破浪会有时,直挂云帆济沧海。 1.认识计算机 1.计算机网络是由计算机和通讯构成的,网络研究的是“通信”。 ------1946 世界上第一台计算机 2.终端:只有输入和输出功能,没有计算和处理功能。 3.数据:一串…...
)
SWIFT介绍和学习(简单入门级别)
SWIFT介绍和学习 SWIFT功能介绍SWIFT快速使用LLM及LLM最佳实践(LLM系列文章)部署指南 vllm非官方介绍资料 项目地址:https://github.com/modelscope/swift 任何有疑惑的地方,参考项目首页readme寻求答案 SWIFT功能介绍 SWIFT&…...

智慧城市:提升城市治理能力的关键
目录 一、智慧城市的概念及特点 二、智慧城市在提升城市治理能力中的应用实践 1、智慧交通:提高交通治理效率 2、智慧政务:提升政府服务水平 3、智慧环保:加强环境监测与治理 4、智慧安防:提高城市安全水平 三、智慧城市在…...
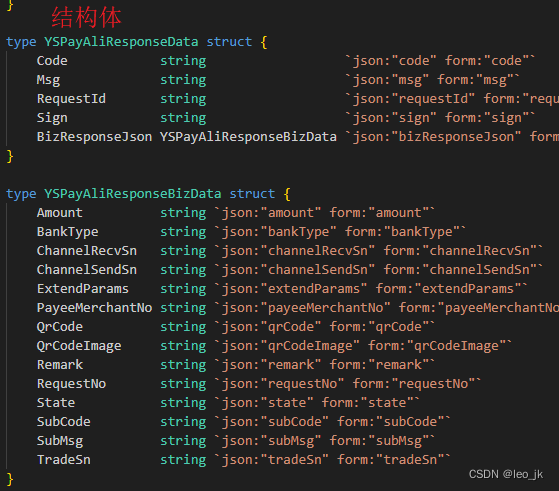
golang 对接第三方接口 RSA 做签(加密) 验签(解密)
一、过程 1.调用第三方接口前,一般需要按规则将参数按key1value1&key2value2 阿斯克码排序,sign参数不参与加密 2.将排序并连接好的参数字符串通过我方的私钥证书(.pem)进行加密得到加密串,当然加密得到的是 []byte 字节流&…...

Spring Data访问Elasticsearch----Elasticsearch存储库Repositories
Spring Data访问Elasticsearch----Elasticsearch存储库Repositories 一、自动创建具有相应映射的索引二、存储库方法的注解2.1 Highlight2.2 SourceFilters 三、基于注解的配置四、Spring命名空间Namespace 本文包括Elasticsearch存储库实现的细节。 例1:示例Book实…...

初探 Cocos Creator: 碰撞与物理系统
前言 不知道你刚开始玩碰撞时,会不会遇到始终无法触发碰撞事件?玩物理系统时,自由落体的刚体会穿过 “地面” 刚体等情况?没错我全都遇到过,那么下面我就用红蓝色方块,简单实战一下 Cocos Creator 的碰撞与…...
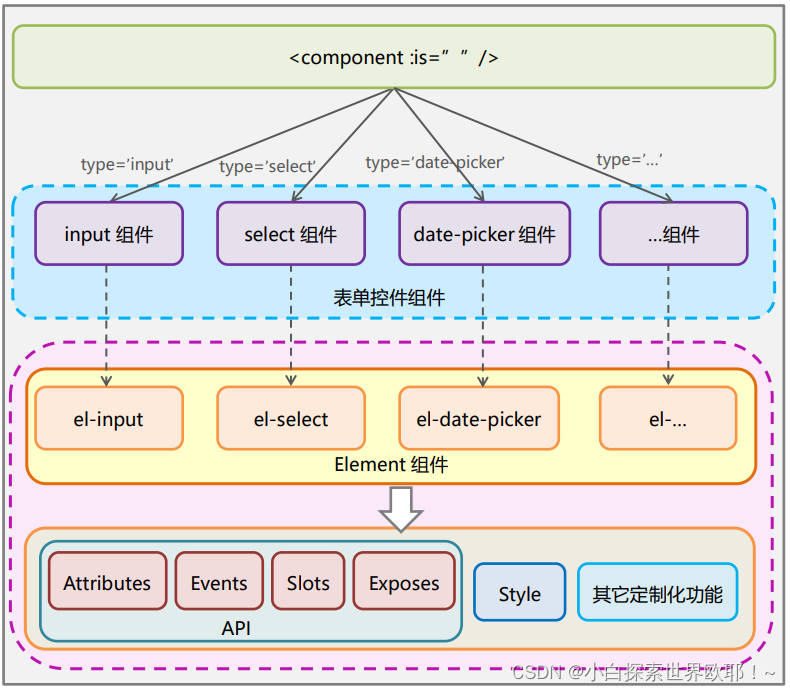
Vue组件封装方案对比——v-if方式与内置component方式
近期在准备搭建一个通用组件库,而公司现有的各个系统也已有自己的组件库只是没抽离出来,但是目前有两套不同的组件封装方案,所以对于方案的选择比较困惑,于是对两种方式进行了对比,结合网上找到的一些开源组件库进行分…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
