Dynamic Movement Primitives (DMP) 学习
Dynamic Movement Primitives (DMP) 学习
【知乎】Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真
1. DMP的建模过程
链接:Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 - 知乎 (zhihu.com)
沙漏大佬!!!!!!!!!!
通过预编程来规划参考轨迹比较复杂。
示教是一种比较简单直观的方法,我们可以让有经验的人带着机器人先完成一次任务,然后让机器人自动学习其中的过程,从而省去编程的复杂过程。
- 能够使用少量的参数来建模示教的轨迹,通过这些参数能够快速地复现示教轨迹
- 在复现示教轨迹的时候能够增加一些任务参数来泛化和改变原始轨迹
采用 “吸引点” 模型,是自稳定的二阶动态系统,通过改变这个 “吸引点” 来改变系统的最终状态,从而达到修改轨迹目标位置的目的。
最简单最常用的二阶系统就是弹簧阻尼系统(PD控制器)
y¨=αy(βy(g−y)−y˙)\ddot y = \alpha_{y}(\beta_{y}(g-y)-\dot y) y¨=αy(βy(g−y)−y˙)
yyy 表示系统状态(例如关节角度), y˙\dot yy˙ 和 y¨\ddot yy¨ 分别表示 yyy 的一阶导数和二阶导数。 ggg 表示目标状态,最后系统会收敛到这个状态上。 αy\alpha_{y}αy 和 βy\beta_{y}βy 是两个常数,相当于PD控制器中的P参数和D参数。
不足之处:能够让系统收敛到目标状态 ggg ,却无法控制收敛的过程量,比如轨迹的形状。
在这个PD控制器上叠加一个非线性项来控制收敛过程量
把DMP看作是一个PD控制器与一个轨迹形状学习器的叠加
通过改变目标状态 ggg 和非线性项 fff 来调整我们的轨迹终点和轨迹形状 →\rightarrow→ 空间上的改变
y¨=αy(βy(g−y)−y˙)+f\ddot y = \alpha_{y}(\beta_{y}(g-y)-\dot y)+f y¨=αy(βy(g−y)−y˙)+f
fff 就是非线性函数,用于控制过程变量。
不足之处:收敛速度不确定。
在速度曲线 y˙\dot yy˙ 上增加一个放缩项 τ\tauτ 来实现
τ2y¨=αy(βy(g−y)−τy˙)+f\tau^{2}\ddot y = \alpha_{y}(\beta_{y}(g-y)-\tau\dot y)+f τ2y¨=αy(βy(g−y)−τy˙)+f
DMP的核心公式!
2. 非线性函数 fff 的确定
叠加非线性函数 fff 的目的:能够用来改变轨迹的形状
非线性函数 fff 本质上可以看作给系统施加的 “外力” ,因为 fff 直接作用到轨迹的二阶导数上,与加速度类似
通过 多个 非线性基函数 的 归一化 线性叠加 来实现
f(t)=∑i=1NΦi(t)ωi∑i=1NΦi(t)f(t)=\frac{\sum_{i=1}^{N}\Phi_{i}(t)\omega_{i}}{\sum_{i=1}^{N}\Phi_{i}(t)} f(t)=∑i=1NΦi(t)∑i=1NΦi(t)ωi
这个基函数所使用的就是高斯基函数(径向基函数)ωt\omega_tωt 为每个基函数对应的权重, NNN 为基函数的个数。
不足之处:这样的非线性函数与时间 ttt 高度相关,无法同时建模多个自由度的轨迹,并让它们在时间上与控制系统保持同步。
解决方法:去时间化。
离散型 DMP →\rightarrow→ 时间无关的量 xxx 代替 ttt ;
节律型 DMP →\rightarrow→ 时间无关的相位 ϕ\phiϕ 代替 ttt ;
3. 离散型 DMP
离散型DMP 对应 连续的节律型DMP,主要的目的是为了解决笛卡尔空间的轨迹规划问题。
离散型 DMP →\rightarrow→ 时间无关的量 xxx 代替 ttt , xxx 来自于一个一阶系统(正则系统)
τx˙=−αxx\tau \dot x=-\alpha_{x} x τx˙=−αxx
推导:
τdxdt=−αxxτdxx=−αxdt∫τdxx=∫−αxdtτlnx=−αxtx=exp{−αxτt}\tau \frac{dx}{dt}=-\alpha_{x}x \\ \tau \frac{dx}{x} =-\alpha_{x}dt \\ \int \tau \frac{dx}{x} = \int -\alpha_{x}dt \\ \tau \ln x = -\alpha_{x}t \\ x = \exp\{-\frac{\alpha_{x}}{\tau}t\} τdtdx=−αxxτxdx=−αxdt∫τxdx=∫−αxdtτlnx=−αxtx=exp{−ταxt}
αx\alpha_{x}αx 是一个常数,常数 τ\tauτ 与DMP公式的 τ\tauτ 保持一致。
当两个常数 αx\alpha_{x}αx 和 τ\tauτ 都是正数的时候,t→∞t\rightarrow \infint→∞ 导致变量 xxx 趋向于 0。
两个常数 αx\alpha_{x}αx 和 τ\tauτ 都将会影响到系统的收敛速度。
因此,可以设置变量 xxx 为任意一个非零正值,这个非零正值本身蕴含着时间 ttt 的信息(因为 xxx 本身就是 ttt 的函数)。变量 xxx 可以看成一个相位变量。
存在某个时刻 t0t_{0}t0 使得变量 x=exp{−αxτt0}=1x=\exp\{-\frac{\alpha_{x}}{\tau}t_{0}\}=1x=exp{−ταxt0}=1 的时候表示系统处于初始状态,当变量 x=exp{−αxτ∞}=0x=\exp\{-\frac{\alpha_{x}}{\tau}\infin\}=0x=exp{−ταx∞}=0 的时候表示系统收敛到了目标状态。
非线性函数在相位 xxx 的存在下而重新定义。
f(x,g)=∑i=1NΦi(x)ωi∑i=1NΦi(x)x(g−y0)f(x,g)=\frac{\sum_{i=1}^{N}\Phi_{i}(x)\omega_{i}}{\sum_{i=1}^{N}\Phi_{i}(x)}x(g-y_{0}) f(x,g)=∑i=1NΦi(x)∑i=1NΦi(x)ωix(g−y0)
xxx 项:保证这个函数能收敛到0;(g−y0)(g-y_{0})(g−y0)项:是这个函数的 “幅值” ,包含着想要改变轨迹的变化的程度
不足之处:轨迹的目标位置与起始位置都在同一个位置的情况来说,g−y0=0g-y_{0}=0g−y0=0,那 fff 就没有存在的意义。
注意:对于三维空间中的轨迹来说,不是每个维度都要一致才叫一致。
只要其中有任何一个维度是一致的,那么这个维度的 fff 就会失效,我们就无法学习得到轨迹的形状。
4. 离散型 DMP 中基函数的选择问题
径向基函数,实际就是概率中正态分布的 “核” 函数。
Φi(x)=exp(−12σi2(x−ci2))\Phi_{i}(x) = \exp(-\frac{1}{2\sigma_{i}^{2}}(x-c_{i}^{2})) Φi(x)=exp(−2σi21(x−ci2))
σi\sigma_{i}σi 和 cic_{i}ci 基函数 Φi(x)\Phi_{i}(x)Φi(x) 的宽度和中心位置,这些都是通过示教过程中学习学到的

之前描述可知,变量 xxx 可以从 1 收敛到 0.0 。而一系列径向基函数要在区间 [0,1][0,1][0,1] 上分布,那么这就意味着这些径向基函数的中心值应该均匀分布一些,这样都能照顾得到。

增加不同权值后的最终非线性函数 fff ,可见都能收敛到最终值 0.0 。
而由于正则系统最终都能收敛到 0.0 ,从而保证了随着时间推进,非线性项起的作用越来越小,系统最终会趋于稳定,而不会发散失控。
不足之处:变量 xxx 上的均匀布置并不代表时间上的均匀布置。我们增加径向基函数的本质是要增加示教轨迹不同阶段的可改变程度,如果径向基函数都 “扎堆” 在前期,而后期比较少的话,后期改变的程度很有限的。

大部分的高斯基函数都集中在初始时刻附近,而随着时间的进行,基函数所起的作用越来越小,这样会导致在曲线拟合的初始阶段效果很好,而在趋于目标位置的末段曲线的拟合效果变差,甚至是无法拟合。这就导致变量 x=1x=1x=1 的时候收敛很快,变化很好;但是变量 x=0.0x=0.0x=0.0 的时候,变化很慢。
从上面的图可以看出,时间轴在 1∼21\sim 21∼2 秒左右径向基函数很多,但是在 222 秒之后就很少径向基函数了,那么在前 222 秒变化会很 “灵敏”,但是2秒之后就变化很 “愚钝” 。

解决思路:用时间上的均匀布置的点 t1,t2⋯t_{1},t_{2}\cdotst1,t2⋯ 的对应的 xxx 变量 x1,x2⋯x_1,x_2\cdotsx1,x2⋯ 来作为中心点。
因为径向基函数本身就关于变量 xxx 的函数,那么这组变量 x1,x2⋯x_1,x_2\cdotsx1,x2⋯ 肯定能覆盖在 xxx 区间 [0,1][0,1][0,1] 上。
正则系统 xxx 的收敛速度是越来越慢的,那么如果我们把每个基函数的宽度在 xxx 的维度上设定为一样的,就会导致早期的基函数持续时间短,而后期的基函数持续时间长。
因为时间越往后,经过同样宽度的 xxx 所需的时间越多,从而导致在时间的维度上出现基函数的宽度不一致的问题,时间约靠后的宽度越大。
因此,基函数的宽度应该随着时间的递增而递减,从而保证在时间的维度上,每个基函数的宽度也是均匀的。
最后得到的结果是:
hi=NBFscih_{i} = \frac{N_{BFs}}{c_{i}} hi=ciNBFs
NBFsN_{BFs}NBFs 的径向基函数的数量。
5. 节律型DMP
因为自己研究暂未涉及到节律型MDP,所以这部分就先仅仅了解下~
节律型 DMP(Rhythmic DMP)是解决连续周期的节律型轨迹规划问题的。
周期性曲线我们需要进行改变和泛化的往往是曲线的幅值与频率,从而获取不同的曲线来满足不同的任务需求。
在节律型DMP中,目标状态是轨迹的中心位置(或者平均位置)。我们可以理解为在做周期性运动时,轨迹会 “围绕” 这个中心位置做往复运动。
节律型DMP的 x(ϕ)x(\phi)x(ϕ) 来自另一个正则系统,该系统收敛于一个极限环(Limit cycle)。
τϕ˙=1,ϕ∈[0,2π]\tau\dot\phi =1,\phi\in[0,2\pi] τϕ˙=1,ϕ∈[0,2π]
节律型 DMP 的非线性函数
f(x,g)=∑i=1NΦi(x)ωi∑i=1NΦi(x)rf(x,g)=\frac{\sum_{i=1}^{N}\Phi_{i}(x)\omega_{i}}{\sum_{i=1}^{N}\Phi_{i}(x)}r f(x,g)=∑i=1NΦi(x)∑i=1NΦi(x)ωir
基函数是冯米塞斯函数
Φi=exp(hi⋅(cos(ϕ−ci)−1))\Phi_{i}=\exp(h_i\cdot(\cos(\phi-c_{i})-1)) Φi=exp(hi⋅(cos(ϕ−ci)−1))
通过 rrr 来控制曲线运动的幅值。
在DMP模型的参数学习阶段,我们可以设置 r=1r=1r=1,这样可以保证DMP可以学习到与示教曲线一样的幅值;
在轨迹复现阶段,我们可以通过给定不同的 rrr 来得到不同的幅值。
6. DMP模型学习和轨迹复现
给定示教的轨迹 [ydemo,y˙demo,y¨demo][y_{demo},\dot y_{demo},\ddot y_{demo}][ydemo,y˙demo,y¨demo]
需要确定的参数:
| PD控制器 | 基函数 | 正则系统 |
|---|---|---|
| αy\alpha_{y}αy βy\beta_{y}βy | 基函数个数NNN 宽度cic_{i}ci 中心值σi\sigma_{i}σi 权重ωi\omega_{i}ωi | αi\alpha_{i}αi |
常数可以自己调整,也可以用强化学习自动改参数
论文采用了局部加权归回方法LWR(Locally Weighted Regression)来学习得到
- 它的计算效率高
- 实时性比较好
- LWR中每个模型Component的学习过程是相互独立的
目标函数 ftargetf_{target}ftarget ,实际就是做了移项
ftarget=τ2y¨demo−αy(βy(g−ydemo)−τy˙demo)f_{target}=\tau^{2}\ddot y_{demo}-\alpha_{y}(\beta_{y}(g-y_{demo})-\tau\dot y_{demo}) ftarget=τ2y¨demo−αy(βy(g−ydemo)−τy˙demo)
而从前面我们已经分析了非线性项 fff 是通过基函数加权得到的,因此我们需要构造损失函数,然后使用最优化方法LWR来学习得到这些基函数的模型参数。
构造平方损失函数,然后用最优化方法求解。
Ji=∑t=1PΦi(t)(ftarget(t)−ωiξ(t))2J_{i}=\sum_{t=1}^{P}\Phi_{i}(t)(f_{target}(t)-\omega_{i}\xi(t))^{2} Ji=t=1∑PΦi(t)(ftarget(t)−ωiξ(t))2
推导:
f(x,g)=∑i=1NΦi(x)ωi∑i=1NΦi(x)x(g−y0)∑i=1NΦi(x)f(x,g)=∑i=1NΦi(x)ωix(g−y0)f(x,g)=\frac{\sum_{i=1}^{N}\Phi_{i}(x)\omega_{i}}{\sum_{i=1}^{N}\Phi_{i}(x)}x(g-y_{0}) \\ \sum_{i=1}^{N}\Phi_{i}(x)f(x,g)=\sum_{i=1}^{N}\Phi_{i}(x)\omega_{i}x(g-y_{0}) \\ f(x,g)=∑i=1NΦi(x)∑i=1NΦi(x)ωix(g−y0)i=1∑NΦi(x)f(x,g)=i=1∑NΦi(x)ωix(g−y0)
取每一个子项,则有:
Φi(x)f(x,g)=Φi(x)ωix(g−y0)\Phi_{i}(x)f(x,g) = \Phi_{i}(x)\omega_{i}x(g-y_{0}) Φi(x)f(x,g)=Φi(x)ωix(g−y0)
最后把 ftargetf_{target}ftarget 替换 f(x,g)f(x,g)f(x,g) ,再转换成平方损失,就有上述表达式。
PPP 表示整条轨迹的总时间步数(即 tdt\frac{t}{dt}dtt ),对于离散型DMP,ξ(t)=x(t)(g−y0)\xi(t)=x(t)(g−y_0)ξ(t)=x(t)(g−y0) ,对于节律型DMP,ξ(t)=r\xi(t)=rξ(t)=r。上述损失函数的求解过程是一个加权线性回归问题。
ωi=sTΓiftargetsTΓis\omega_{i} = \frac{s^{T}\Gamma_{i}f_{target}}{s^{T}\Gamma_{i}s} ωi=sTΓissTΓiftarget

2023/03/06 - 上午 - 先看到这里,去吃饭了~
2023/03/06 - 下午 - 对文案又做了一些解释~
相关文章:

Dynamic Movement Primitives (DMP) 学习
Dynamic Movement Primitives (DMP) 学习 【知乎】Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 1. DMP的建模过程 链接:Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 - 知乎 (zhihu.com) 沙漏大佬!!&am…...
2023王道考研数据结构笔记第五章——树
第五章 树 5.1 树的基本概念 树是n(n≥0)个结点的有限集合,n 0时,称为空树。 空树——结点数为0的树 非空树——①有且仅有一个根节点 ②没有后继的结点称为“叶子结点”(或终端结点) ③有后继的结…...

setState函数是异步的还是同步的?
setState函数是异步的还是同步的? 可能很多同学在看到这个问题的时候,甚至搞不清楚这个问题在问什么。 不要慌,我们看一下下面这个例子,首先我们创建一个类组件,这个类组件中,我们定义了state是一个对象,对象中有一个…...
vue3+ts:约定式提交(git husky + gitHooks)
一、背景 Git - githooks Documentation https://github.com/typicode/husky#readme gitHooks: commit-msg_snowli的博客-CSDN博客 之前实践过这个配置,本文在vue3 ts 的项目中,再记录一次。 二、使用 2.1、安装 2.1.1、安装husky pnpm add hus…...
TSP 问题求解的最好方法 LKH
目前可以查到的最好的方法求解TSP问题是 LKH,所以本篇文章介绍如何使用Matlab 调用LKH 参考文档:用matlab调用迄今为止最强悍的求解旅行商(TSP)的算法-LKH算法_wx6333e948c3602的技术博客_51CTO博客 【LKH算法体验】用matlab调用…...
RocketMQ5.1控制台的安装与启动
RocketMQ控制台的安装与启动下载修改配置开放端口号重启防火墙添加依赖编译 rocketmq-dashboard运行 rocketmq-dashboard本地访问rocketmq无法发送消息失败问题。connect to <公网ip:10911> failed下载 下载地址 修改配置 修改其src/main/resources中…...
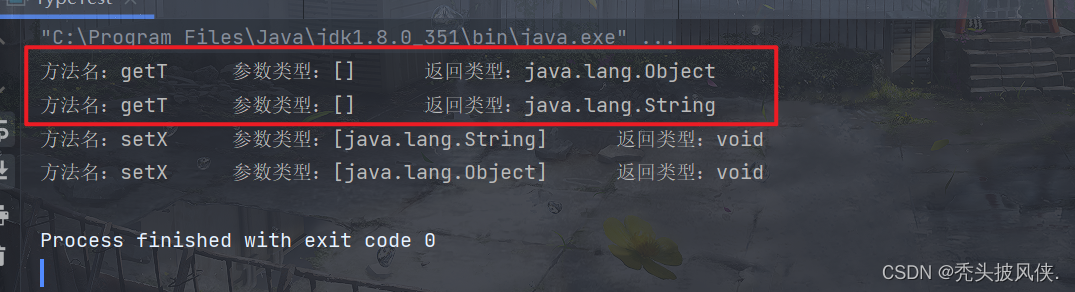
【java基础】类型擦除、桥方法、泛型代码和虚拟机
文章目录基础说明类型擦除无限定有限定转换泛型表达式方法类型擦除(桥方法)关于重载的一些说明总结基础说明 虚拟机没有泛型类型对象一所有对象都属于普通类。在泛型实现的早期版本中,甚至能够将使用泛型的程序编译为在1.0虚拟机上运行的类文…...

十家公司有九家问过的软件测试面试题,最后一题我猜你肯定不会
最近面试了一些测试方面相关的岗位,通过牛客等途径也看了不少的面经,发现大部分人面试题目都有很多相似点,结合自己的一些面试经历,现在分享一些我面试中碰到过的问题 常见的面试题 1、jmeter的加密参数如何入参? 2…...

C++核心知识(三)—— 静态成员(变量、函数、const成员)、面向对象模型(this指针、常函数、常对象)、友元、数组类、单例模式
【上一篇】C核心知识(二)—— 类和对象(类的封装)、对象的构造和析构(浅拷贝、深拷贝、explicit、动态分配内存)1. 静态成员在类定义中,它的成员(包括成员变量和成员函数),这些成员可以用关键字static声明为…...

RocketMQ【3】Rocketmq集群部署(多master多slave)异步复制
系列文章目录 RocketMQ【1】linux安装配置Rocketmq(单机版) RocketMQ【2】Rocketmq控制台安装启动(单机版) 文章目录系列文章目录一、异步复制的优缺点1、优点2、缺点二、架构1、架构图2、介绍3、机器配置三、配置1、master节点配…...

魏玛早春 木心
<font face“黑体” color#CD5C5C size6 魏玛早春 木心 温带每个季节之初 总有神圣气象恬漠地 剀切地透露在风中 冬天行将退尽 春寒嫩生生 料峭而滋润 漾起离合纷纷的私淑记忆 日复一日 默认季节的更替 以春的正式最为谨慎隆重 如果骤尔明暖 鸟雀疏狂飞鸣 必定会吝悔似的剧…...

关于Scipy的概念和使用方法及实战
关于scipy的概念和使用方法 什么是Scipy Scipy是一个基于Python的科学计算库,它提供了许多用于数学、科学、工程和技术计算的工具和函数。Scipy的名称是“Scientific Python”的缩写。 Scipy包含了许多子模块,其中一些主要的子模块包括: …...

第二章Linux操作语法1
文章目录vi和vim常用的三种模式vi和vim快捷键Linux开机,重启用户管理用户信息查询管理who和whoami用户组信息查询管理用户和组的相关文件实用指令集合运行级别帮助指令manhelp文件管理类pwd命令ls命令cd命令mkdir命令rmdir命令rm命令touch命令cp指令mv指令文件查看类…...

linux内核调度问题分析
目录 一、调度场景分析 不支持内核抢占的内核 支持内核抢占 二、如何让新进程执行 三、调度的本质 一、调度场景分析 假如内核只有3个线程,线程0创建线程1和线程2.当系统时钟到来时,时钟中断处理函数会检查是否有进程需要调度。当有进程需要调度时…...
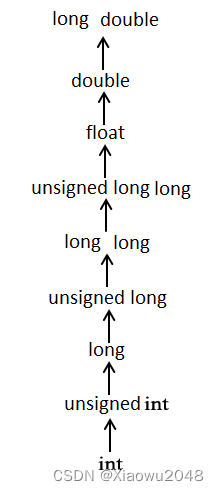
C语言-基础了解-25-C强制类型转换
C强制类型转换 一、强制类型转换 强制类型转换是把变量从一种类型转换为另一种数据类型。例如,如果您想存储一个 long 类型的值到一个简单的整型中,您需要把 long 类型强制转换为 int 类型。您可以使用强制类型转换运算符来把值显式地从一种类型转换为…...

【Python】如何安装 Allure 工具进行自动化测试
Allure 是一种流行的工具,用于以人类可读的格式生成测试报告,从而更容易理解和分析测试结果。在这篇博客中,我们将探索如何在 Windows 机器上安装 Allure 及其依赖项。 1 Prerequisites 先决条件 在田辛老师开始之前,请确保您的…...

nginx七大核心应用场景详解 解决生产中的实际问题 二次开发扩展
nginx七大核心应用场景详解 & 解决生产中的实际问题1、nginx的安装与简单配置1.1、环境准备1.2、nginx基本操作指令:1.3、安装成系统服务1.4、conf 配置文件说明2、虚拟主机2.1、nginx多主机配置2.2、二级域名与短网址解析3、基于反向代理的负载均衡3.1、跳转到…...

Java 整合 Redis
文章目录Java 整合 Redis一、Jedis二、Spring-Data-RedisJava 整合 Redis Redis 在项目中我们主要用来做缓存,就像我们用 MySQL 做持久层数据一样。Redis 的客户端有两种实现方式: 一是直接调用 Jedis 来实现,类似于 Java 使用 JDBC 操作数…...
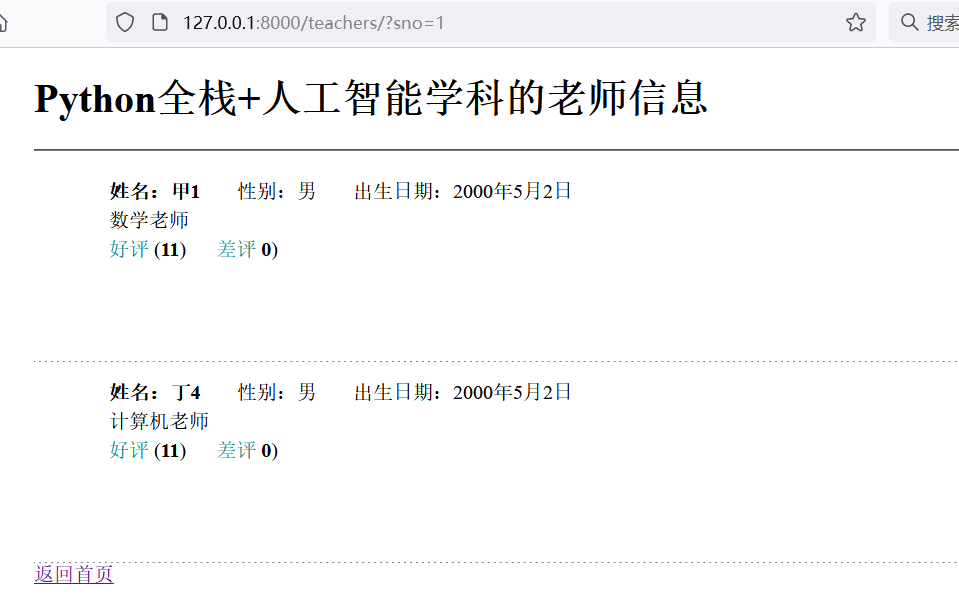
Django实践-03模型-02基于admin管理表
文章目录Django实践-03模型利用Django后台管理模型1. 将admin应用所需的表迁移到数据库中。2. 创建访问admin应用的超级用户账号,3. 运行项目4.注册模型类5.对模型进行CRUD操作。6.实现学科页和老师页效果1. 修改polls/views.py文件。2.修改templates/polls/subject…...

如何安装python
windows安装 下载安装包 登录python官网 https://www.python.org/ 点击downloads 置顶下载的是最新的python版本 如果想下载指定版本往下翻找 安装程序 点击即可下载,然后打开下载的exe程序 勾选添加pythonexec到path,也就是添加到环境变量 使用a…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
