手机可以格式化存储卡吗?格式化以后出现什么情况
随着智能手机的普及,存储卡(如SD卡、MicroSD卡等)已成为手机存储扩展的重要工具。然而,在使用过程中,我们有时可能会遇到需要格式化存储卡的情况。那么,手机能否直接格式化存储卡呢?格式化后存储卡会发生哪些变化?本文将为您解答这些问题,并深入探讨手机格式化存储卡的相关知识和注意事项。

一、手机能否格式化存储卡?
大部分智能手机都支持对存储卡进行格式化操作。通常,您可以在手机的“设置”或“存储”选项中找到格式化存储卡的选项,如恢复出厂设置。下面以Redmi Note 11为例进行操作:
- 打开手机,进入主界面,并点击“设置”图标进入手机设置。
- 在设置界面中,向下滑动找到“我的设备”选项,点击进入。
- 在我的设备页面中,继续向下滑动,找到“恢复出厂设置”选项,点击进入。
- 在恢复出厂设置界面中,如果只想格式化手机内置存储的数据,选择“清除所有数据”即可;如果想同时格式化SD卡上的数据,则选择清除以下手机数据中的“SD卡所有数据”。
- 选择格式化选项后,系统会提示输入手机的解锁密码或小米账号的密码,以确保操作是手机主人进行的。输入密码后,点击确认,等待格式化完成即可。
二、格式化存储卡后的影响
数据清除:格式化存储卡会删除存储卡上的所有文件和数据,包括照片、视频、文档等。因此,在格式化前请务必备份重要数据。
性能恢复:有时,存储卡可能会出现读写速度变慢、文件丢失或损坏等问题。格式化存储卡可以恢复其性能,提高读写速度。
文件系统更新:格式化操作还可能更新存储卡的文件系统,使其与手机系统更加兼容。
三、格式化存储卡的注意事项
备份数据:如前所述,格式化会清除存储卡上的所有数据,因此请务必在格式化前备份重要数据。
选择合适的文件系统:在格式化时,有时可以选择不同的文件系统(如FAT32、exFAT、NTFS等)。请根据您的手机系统和存储卡容量选择合适的文件系统。
避免频繁格式化:频繁格式化会对存储卡造成一定的损耗,影响其使用寿命。因此,建议在必要时再进行格式化操作。
四、格式化存储卡数据怎么恢复
存储卡里面通常会存放着我们重要的照片、视频和文件,一旦这些数据丢失,可能会给我们的生活带来很大困扰。那么,存储卡数据丢失能恢复吗?
要恢复格式化的存储卡数据,可以尝试使用数据恢复软件,如支持扫描和预览的云骑士数据恢复软件预判数据可恢复性。下面是具体格式化存储卡数据怎么恢复步骤:
步骤1:将存储卡通过读卡器连接到电脑中,并打开恢复软件,选择“U盘/内存卡恢复”选项。
步骤2:在软件中选择存储卡作为扫描目标,启动扫描,并等待软件扫描完整个存储卡。
步骤3:在扫描结果中查找需要恢复的数据,可以根据文件类型或文件名等筛选,然后预览一下。
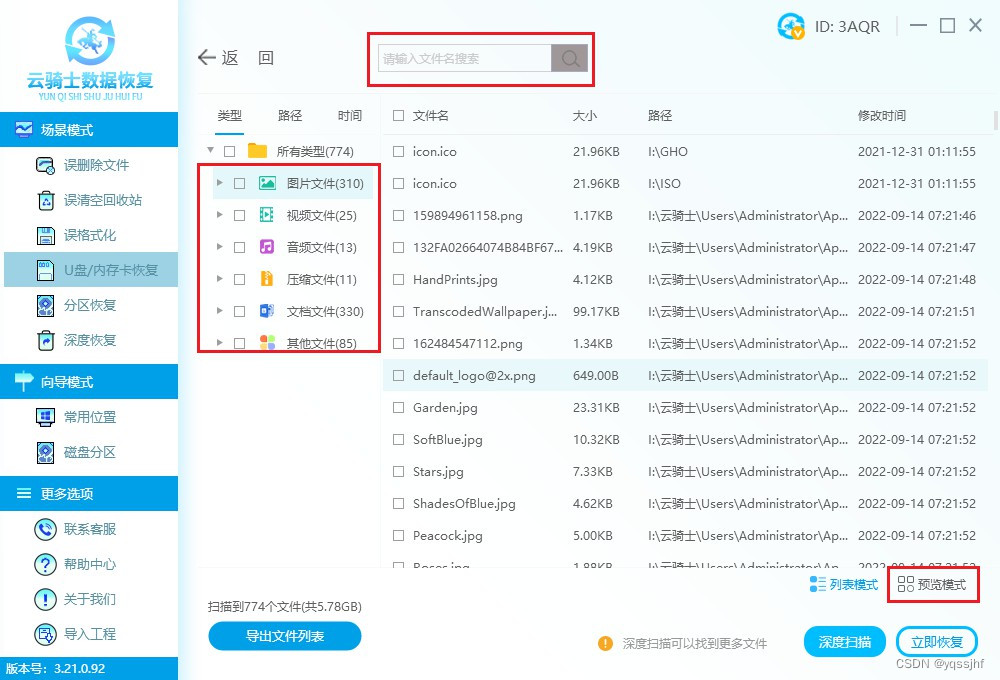
步骤4:最后选择要恢复的文件,并将其保存到另一个存储设备上,以避免覆盖原始数据。
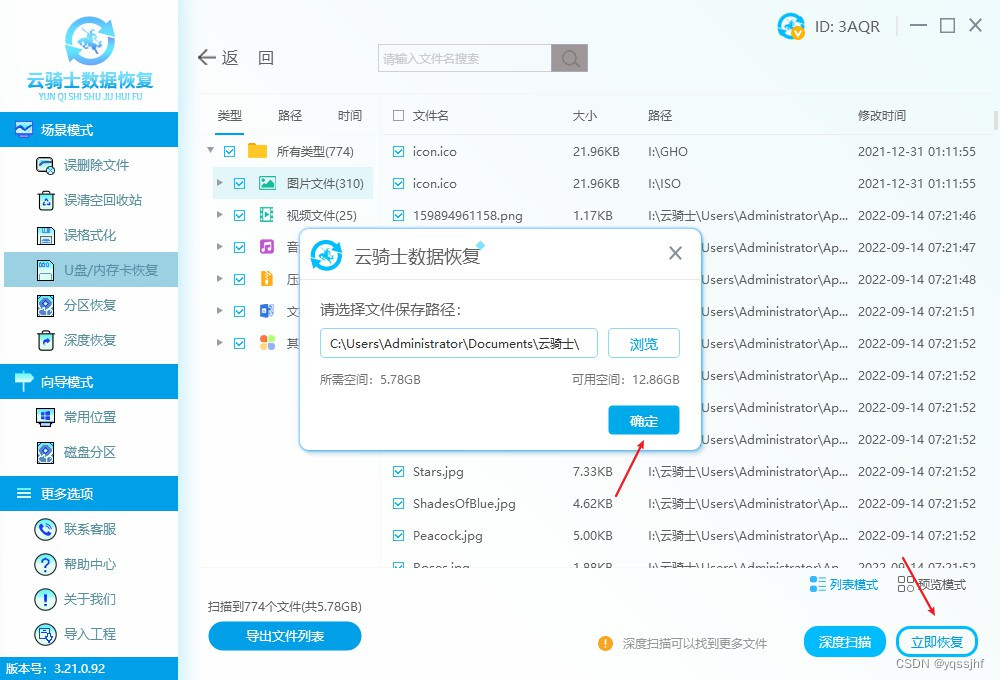
请注意,在使用数据恢复软件时,要确保不要将恢复的数据保存到原存储卡上,以免覆盖原有数据。此外,格式化存储卡后,想要提高数据恢复率,建议尽快停止使用存储卡,并尝试恢复数据。
结尾:
通过本文的探讨,我们了解了手机可以格式化存储卡以及格式化后的影响。格式化存储卡可以恢复其性能、提高读写速度,并更新文件系统,但也会清除存储卡上的所有数据。因此,在进行格式化操作时,请务必备份重要数据,并选择合适的文件系统。同时,也需要注意避免频繁格式化,以延长存储卡的使用寿命。
往期推荐:
u盘数据删除或者移除了怎么办?冷静,恢复指南来帮你
移动硬盘数据可以保存多长时间?数据丢失怎么办
u盘很卡是什么原因造成的?怎么解决
相关文章:

手机可以格式化存储卡吗?格式化以后出现什么情况
随着智能手机的普及,存储卡(如SD卡、MicroSD卡等)已成为手机存储扩展的重要工具。然而,在使用过程中,我们有时可能会遇到需要格式化存储卡的情况。那么,手机能否直接格式化存储卡呢?格式化后存储…...
亚马逊AWS展示高效纠错的全新量子比特!
亚马逊网络服务公司(AWS)在量子计算的纠错技术领域取得了显著成就,极大地简化了量子系统的复杂性和资源需求。他们的研究人员通过采用“双轨擦除”量子比特(dual-rail erasure qubit)技术,有效地克服了量子…...

FEX-Emu在Debian/Ubuntu系统使用
FEX-Emu在Debian/Ubuntu系统使用 1. Debootstrap子系统安装(可选)2. Debian/Ubuntu依赖包安装3. 获取FEX-Emu源码并编译4. 根文件系统RootFS安装5. 基于 FEX-Emu 运行应用 1. Debootstrap子系统安装(可选) sudo apt-get install …...

docker 不同架构镜像融合问题解决
1、背景 docker 作为目前容器的标准之一,但是对于多种架构的平台的混合编译支撑不是很好。因此衍生了镜像融合,分别将多种不同的架构构建好,然后将镜像进行融合上传。拉取镜像的会根据当前系统的架构拉取不同的镜像,也可以通过 -…...

windows_anaconda 安装pytorch
查看CUDA版本 cmd nvidia-smi # NVIDIA-SMI 546.56 Driver Version: 546.56 CUDA Version: 12.3nvcc --version # nvcc: NVIDIA (R) Cuda compiler driver # Copyright (c) 2005-2023 NVIDIA Corporation # Built on Wed_Nov_22_10:30:42_Pacific_Standard_Time_2023 # C…...

IP SSL证书注册流程
使用IP地址申请SSL证书,需要用公网IP地址申请,申请之前确保直接的IP地址可以开放80或者443端口两者选择1个就好,端口不需要一直开放,只要认证的几分钟内开放就可以了,然后IP地址根目录可以上传txt文件。 IP SSL证书认…...

shentou思路流程
信息收集: 1、获取域名whois信息也就是所谓的资产收集 2、服务器子域名、旁站、c段查询 3、服务器操作系统类型、版本、补丁状况、开放端口:22 ssh 80 web 445 3389.。。 4、web中间件类型、版本、网站目录结构、使用的waf等设备 5、数据库类型、版…...
航空实时监控
1、从Kafka中读取飞机数据,并进行清洗 此步骤在前面的“使用Spark清洗统计业务数据并保存到数据库中”任务阶段应该已经完成。如果没有完成,请参考源代码自行完成。核心类主要有三个:SparkStreamingApplication类、SparkUtil类和MapManager类…...

第十四届蓝桥杯JavaB组省赛真题 - 幸运数字
进制转换可以参考如下的十进制,基本一样的,只是把10变成了其他数字, sum就是各个数位之和 public static int myUtil(int n) {int sum 0;while(n > 0) {sum n % 10;n / 10;}return sum;} 注意: 如果写在同一个类里面&…...
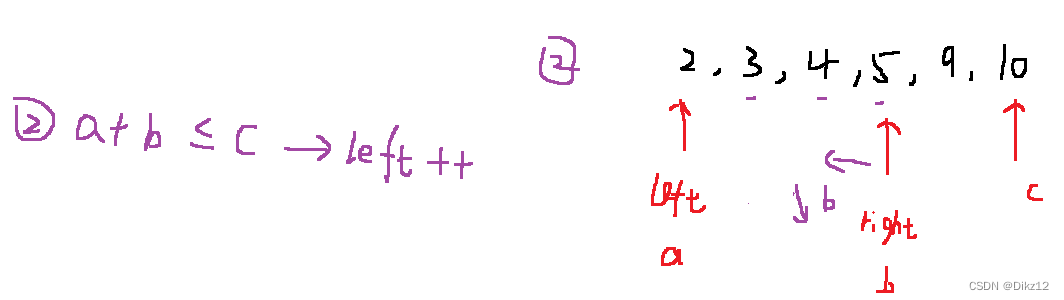
【练习】双指针算法思想
🎥 个人主页:Dikz12🔥个人专栏:Java算法📕格言:那些在暗处执拗生长的花,终有一日会馥郁传香欢迎大家👍点赞✍评论⭐收藏 目录 1. 移动零 1.1 题目描述 1.2 讲解算法原理 1.3 编…...

Leetcode 20. 有效的括号
心路历程: 看到括号问题直接想到栈,但是纠结了一下题目中给出的 ‘2. 左括号必须以正确的顺序闭合’ 这一约束,其实这句话的意思简化了题目要求,[(])这样的字符串就不满足要求了。 注意的点: 1、注意最后需要栈为空…...

jupyter | mac jupyter快捷键
【ctrlenter】:是运行选中的单元格,他会停留在此 > 执行 【optionenter】:是运行单元格并且在下面插入一个新的单元格 > 执行 【shiftenter】:是 运行单元格, 并选择下面的单元格 > 执行 【Tab】键用来代码补全 【A】键…...
么样才能用最便捷的方式为Mac提速呢?
Mac是现代人日常工作时必不可少的工具,尤其是在居家办公已经屡见不鲜的当下。视频会议、文档传送、视频剪辑等等。它在工作中扮演的角色越来越重要,所以也导致了它的流畅程度可以在很大程度上影响人们一整天的工作效率和心情。 但是影响Mac的运行和响应速…...

专业前沿问题问答合集10-2——比特币的加密原理
专业前沿问题问答合集10-2——比特币的加密原理 比特币的加密原理 比特币作为一种加密货币,其安全性和功能性主要基于密码学原理和区块链技术。以下是比特币加密原理的关键组成部分: 1. 非对称加密(公钥和私钥) 比特币使用非对称加密技术来确保交易的安全性。每个比特币…...

C++中的流
前言 在 C 中,流(stream)是一种数据传输的抽象概念,用于在程序中对输入和输出进行操作。流分为输入流和输出流,允许数据在程序和外部设备(如键盘、屏幕、文件)之间进行传输。输入流用于从外部获…...

解决vue3中使用v-html,click不生效的问题
问题背景 说明: 前端接收到来自后端的一个长字符串,要求把里面的图片替换成为超链接,并且要通过请求一个接口进行图片下载。 举例说明 就是下列这样的一个字符串:vaddssss[图片](image_p0_f0.png)dsatewafdsaa[图片](image_p1…...
macOS下Java应用的打包和安装程序制作
文章目录 macOS应用程序结构Java应用打包JavaAppLauncherjpackage其它相关JDK命令附录JavaAppLauncher源码链接macOS应用程序结构 macOS通常以dmg或pkg作为软件发行包,安装到/Applications下后,结构比较统一。 info.plist里的CFBundleExecutable字段可以指定入口,如果不指定…...

OpenAI GPT商店面临质量与合规问题;黄仁勋预测:十年内AI将实时生成游戏画面
🦉 AI新闻 🚀 OpenAI GPT商店面临质量与合规问题 摘要:OpenAI旗下的GPT商店因存在大量涉嫌侵权内容、助长学术不诚实行为及违规内容等问题而引起关注。其中包括未经授权使用迪士尼、漫威角色生成内容的GPT模型,以及声称能绕过剽…...

前端根据pdf连接点击下载pdf而不是直接打开
参考地址: https://www.cnblogs.com/jackson-yqj/p/11321275.html /*** 文件链接转文件流下载--主要针对pdf 解决谷歌浏览器a标签下载pdf直接打开的问题* param url :文件链接* param fileName :文件名;* param type :文件类型;*/functio…...

pytorch中的gather函数的定义和作用是什么?
在PyTorch中,gather函数是一个用于从张量(tensor)中收集特定索引位置上的元素的函数。它主要用于高级索引和从张量中提取特定信息。 定义(python) gather函数的基本定义如下: torch.gather(input, dim, i…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
