DP动态规划入门(数字三角形、破损的楼梯、安全序列)
一、动态规划(DP)简介
动态规划(Dynamic Programming,简称DP)是运筹学的一个分支,它是一种通过将复杂问题分解成多个重叠的子问题,并通过子问题的解来构建整个问题的解的算法。在动态规划中,有几个核心概念需要理解:
- 状态:状态通常表示为形如dp[i][j] = val的取值,其中i和j是用于描述和确定状态所需的变量(下标),而val则是该状态对应的值。
- 状态转移:状态转移描述了不同状态之间如何相互转化。这通常可以表示为一个数学表达式,而转移的方向则决定了算法是迭代还是递归地进行。
- 最终状态:最终状态即题目所要求解的状态,也是我们通过动态规划算法最终要得到的答案。
动态规划的关键在于找到子问题之间的重叠关系,并存储这些子问题的解以避免重复计算。通过这种方式,动态规划能够在多项式时间内解决一些看似复杂的问题,如背包问题、最短路径问题等。在实际应用中,动态规划被广泛用于优化和控制问题,以及计算机视觉、生物信息学等领域。
二、动态规划的解题步骤
步骤一:确定状态
首先,需要明确问题的状态表示。在动态规划问题中,状态通常定义为“到第i个为止,xx为j(xx为k)的方案数/最小代价/最大价值”等。这里,“i”、“j”和可能的“k”是状态的参数,它们根据具体问题而定。状态的确切定义取决于问题的性质和所需优化的目标(如最小代价、最大价值或方案数)。
步骤二:确定状态转移方程
状态转移方程是动态规划的核心,确定状态转移方程,即从已知状态得到新状态的方法,并确保按照这个方向一定可以正确地得到最终状态。根据状态转移的方向来决定使用迭代法还是递归法(记忆化)。状态转移方程的确立通常基于问题的特定条件和约束。
步骤三:确定最终状态并输出
最终状态通常是问题的解所对应的状态。在确定了状态转移方程后,我们需要按照这个方程迭代或递归地计算出所有可能的状态,直到达到最终状态。最终状态可能是通过迭代法逐步累积得到,也可能是通过递归法(结合记忆化以避免重复计算)逐步回溯得到。一旦到达最终状态,我们就可以根据问题的要求输出相应的解,如最小代价、最大价值或特定条件下的方案数。
综上所述,这三个步骤——确定状态、确定状态转移方程和确定最终状态并输出——构成了动态规划求解问题的一般框架。在实际应用中,根据具体问题的不同,这些步骤的具体实现方式也会有所不同。
三、线性DP例题
(一)数字三角形(最大路径)

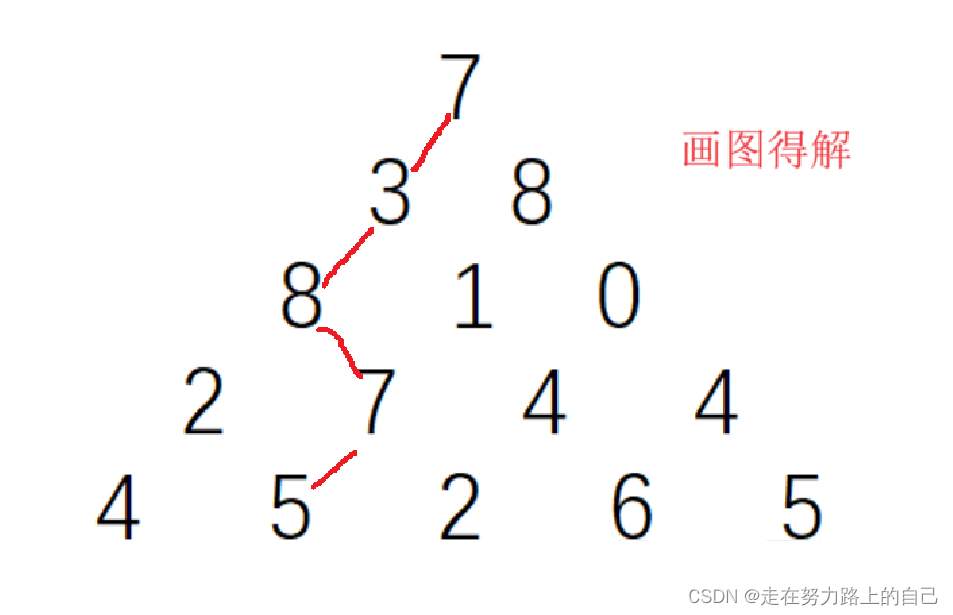
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和(路径上的每一步只可沿左斜线向下或右斜线向下走)。
输入描述
输入的第一行包含一个整数 N(1 ≤ N < 100),表示三角形的行数。
下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 99 之间的整数。
输出描述
输出一个整数,表示答案。
输入样例
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
输出样例
30
思路:
- 从最后一层向上,取最大值累加。
- 确定状态:设状态dp[ i ][ j ] = a[ i ][ j ] + max(dp[ i + 1 ][ j ], dp[ i + 1 ][ j + 1 ]);
- 状态转移方程为dp[i][j]=max(dp[i+1]lj],dp[i +1][j + 1]) ;
- 因为这里需要用下面的状态更新上面的,所以我们应该从下往上进行状态转移。最后输出dp[1][1]
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 105;
ll a[N][N], dp[N][N];int main()
{int n; cin >> n;for (int i = 1; i <= n; ++i)for (int j = 1; j <= i; j++)cin >> a[i][j];for (int i = n; i >= 1; i--)for (int j = 1; j <= i; j++)dp[i][j] = a[i][j] + max(dp[i + 1][j], dp[i + 1][j + 1]);cout << dp[1][1] << '\n';return 0;
}(二)破损的楼梯(方案数)
问题描述:
小蓝来到了一座楼梯前,楼梯共有N级台阶。从第0级台阶出发,小蓝每次可以迈上1级或2级台阶。但是,楼梯上的第a1级、第a2级、第a3级,以此类推,共M级台阶的台阶面已经坏了,不能踩。
小蓝想要到达楼梯的顶端,即第N级台阶,且不能踩到坏台阶。请问他有多少种到达顶端的方案数?由于方案数可能很大,请输出结果对取模的值。

样例输入
6 1 3
样例输出
4
思路:
- 确定状态:状态dp[ i ]表示走到第 i 级台阶的方案数。
- 确定状态转移方程:在正常的楼梯上,我们可以从第i - 1级台阶或第i - 2级台阶走到第 i 级台阶,因此状态转移方程为dp[ i ] = dp[ i-1 ]+dp[ i - 2 ]。
- 然而,如果第 i 级台阶是破损的,则不能走到该台阶,此时我们需要将dp[ i ]设为0。
- 最后我们输出dp[ n ],表示走到第 n 级台阶的方案数
#include<bits/stdc++.h>
using namespace std;
const int p = 1e9 + 7;
int n, m;
int main()
{cin >> n >> m;vector<int>dp(n + 1, 1);int temp = 0;for (int i = 1; i <= m; i++){cin >> temp;dp[temp] = 0;}for (int i = 2; i <= n; i++){if (!dp[i])continue;dp[i] = (dp[i - 1] + dp[i - 2]) % p;}cout << dp[n] << '\n';return 0;
}(三)安全序列(方案数)
问题描述
小蓝是工厂里的安全工程师,他负责在工厂里安全地放置危险品油桶。工厂的空位排列成一条直线,共有n个空位。小蓝需要按照特定的规则在这些空位上放置油桶:每两个油桶之间至少需要k个空位隔开。现在,小蓝想知道有多少种不同的放置方案可以满足这些条件。由于可能的方案数非常大,输出结果需要对10^9 + 7取模。
输入格式
输入包含两个正整数n和k,分别表示空位的数量和每两个油桶之间至少需要的空位数。
输出格式
输出一个整数,表示满足条件的放置方案数对10^9 + 7取模的结果。
样例输入
4 1
样例输出
6
说明
在样例中,有4个空位,每两个油桶之间至少需要1个空位。可能的放置方案有6种,分别是:0000(不放任何油桶),1000,0100,0010,0001和1001(其中1表示放置油桶,0表示不放)。注意,这里的方案数已经对10^9 + 7取模。
评测数据规模
对于所有评测数据,1 ≤ n ≤ 10^9,1 ≤ k ≤ n-1。
思路:
首先,我们定义dp[i]为在前i个空位中放置油桶的方案数。然后,我们需要计算前缀和数组prefix。对于每个位置i,prefix[i]表示从位置0到位置i为止的所有放置方案数的总和。
ll dp[N], prefix[N];
循环遍历判断每个位置之前没有足够的空间放置另一个油桶 。
如果当前位置减去k再减1小于1,则dp[ i ]为1。
否则,dp[ i ]的值等于前缀和数组在( i - 1 - k )位置的值。
if (i - k - 1 < 1)dp[i] = 1;
else dp[i] = prefix[i - 1 - k];设状态dp[ i ]表示以位置i结尾的方案总数,状态转移方程:
但是直接去求和肯定会超时,所以我们需要利用前缀和来优化时间复杂度(注意取模)。
prefix[i] = (prefix[i - 1] + dp[i]) % p;计算到当前位置为止,包括所有符合条件的放置方案数的总和。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll N = 1e6 + 9, p = 1e9 + 7;ll dp[N], prefix[N];int main()
{int n, k; cin >> n >> k;dp[0] = prefix[0] = 1;// 初始化dp和prefix数组的第0项为1,表示空序列的方案数为1for (int i = 1; i <= n; ++i)// 遍历1到n,计算每个位置的dp值和前缀和{if (i - k - 1 < 1)dp[i] = 1;// 如果当前位置减去k再减1小于1,则dp[i]为1// 说明在当前位置之前没有足够的空间放置另一个油桶,// 因此在这种情况下,只能选择不放置油桶,所以'dp[i]'被设为'1'。else dp[i] = prefix[i - 1 - k];// 否则,dp[i]的值等于前缀和数组在(i-1-k)位置的值// 这表示从位置'0'到位置'i-k-1'的所有放置方案数。// 这样做是因为每两个油桶之间需要至少'k'个空位,// 因此'dp[i]'实际上继承了在'i-k-1'位置及之前能放置油桶的所有方案。prefix[i] = (prefix[i - 1] + dp[i]) % p;// 计算到当前位置为止,包括所有符合条件的放置方案数的总和,并将结果模上'p'以防溢出。}cout << prefix[n] << '\n';return 0;
}今天就先到这了!!!

看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。
相关文章:

DP动态规划入门(数字三角形、破损的楼梯、安全序列)
一、动态规划(DP)简介 动态规划(Dynamic Programming,简称DP)是运筹学的一个分支,它是一种通过将复杂问题分解成多个重叠的子问题,并通过子问题的解来构建整个问题的解的算法。在动态规划中&am…...

HBase Shell的应用案例
电商( eshop)平台具有海量数据、高并发访问、高速读写等特征,适合使用HBase分布式数据库进行数据存储。本节通过一个 HBase在电商平台的应用案例,熟练掌握并综合运用HBase Shell命令行终端提供的各种操作命令。 一、电商(eshop)平台的逻辑数据模型 在H…...

Allegro许可管理技巧
在数字化时代,软件许可管理对于企业的运营至关重要。然而,许多企业在实施软件管理过程中会遇到各种问题。Allegro许可管理作为一款高效、合规的管理工具,能够帮助企业解决常见的许可管理问题。本文将深入探讨Allegro许可管理中的实用技巧&…...
34 vue 项目默认暴露出去的 public 文件夹 和 CopyWebpackPlugin
前言 这里说一下 vue.config.js 中的一些 public 文件夹是怎么暴露出去的? 我们常见的 CopyWebpackPlugin 是怎么工作的 ? 这个 也是需要 一点一点积累的, 因为 各种插件 有很多, 不过 我们仅仅需要 明白常见的这些事干什么的即可 当然 以下内容会涉及到一部分vue-cli,…...
Redis 不再“开源”,对中国的影响及应对方案
Redis 不再“开源”,使用双许可证 3 月 20 号,Redis 的 CEO Rowan Trollope 在官网上宣布了《Redis 采用双源许可证》的消息。他表示,今后 Redis 的所有新版本都将使用开源代码可用的许可证,不再使用 BSD 协议,而是采用…...

在CentOS中怎么安装和配置NginxWeb服务器
在CentOS中安装和配置Nginx Web服务器可以通过以下步骤完成: 1. 使用yum安装Nginx: sudo yum install nginx 2. 启动Nginx服务: sudo systemctl start nginx 3. 设置Nginx开机自启动: sudo systemctl enable nginx 4. 配置防火墙规…...

使用docker搭建Fluentd的教程
使用Docker搭建Fluentd的教程 步骤 1: 拉取Fluentd镜像 首先,需要从Docker Hub上拉取Fluentd的官方镜像: docker pull fluent/fluentd:v1.14-debian-1这里使用的是基于Debian的Fluentd 1.14版本的镜像,可以根据需要选择其他版本。 步骤 2…...

Python的re模块进行正则表达式操作时的常用方法[回顾学习]
re 模块是 Python 中用于处理正则表达式的标准库模块。通过 re 模块,可进行字符串匹配、搜索和替换等各种操作。 有几个常用的方法:# re.match(pattern, string):从字符串开头开始匹配模式,并返回匹配对象。适合用于确定字符串是否…...
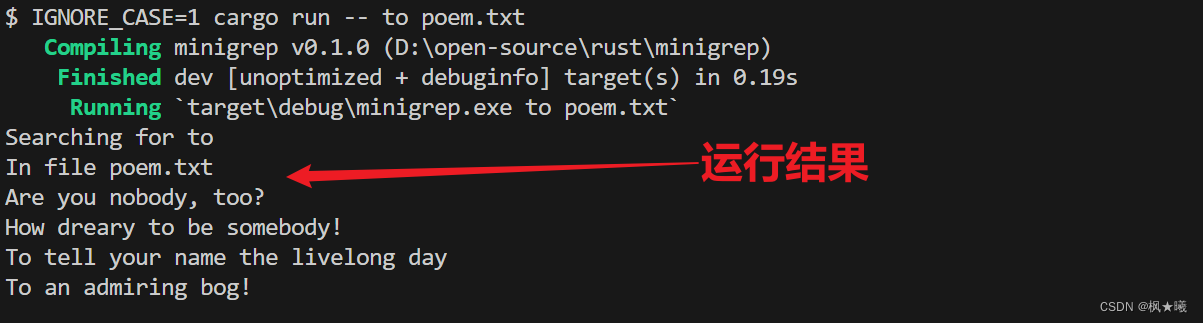
Rust之构建命令行程序(五):环境变量
开发环境 Windows 11Rust 1.77.0 VS Code 1.87.2 项目工程 这次创建了新的工程minigrep. 使用环境变量 我们将通过添加一个额外的功能来改进minigrep:一个不区分大小写的搜索选项,用户可以通过环境变量打开该选项。我们可以将此功能设置为命令行选项,…...

ARMday7
VID_20240322_203313 1.思维导图 2.main.c #include"key_inc.h" //封装延时函数 void delay(int ms) {int i,j;for(i0;i<ms;i){for(j0;j<2000;j){}} } int main() {//按键中断的初始化key1_it_config();key2_it_config();key3_it_config();while(1){printf(&q…...

Ubuntu中安装VSCode的一个指令
问题描述 本来想去VSCode官网上下载软件包,然后双击使用Ubuntu Software安装的,但是安装老不成功。 想用命令行指令dpkg进行安装,虽然能成功,但是后续使用 code . 命令打开VSCode又报错说找不到命令。 解决方式 在命令行中使用…...

生活电子产品拆解分析~汇总目录
一、锂电池电源 ①电子产品拆解分析-暖手宝 ②电子产品拆解分析-电动牙刷 ③电子产品拆解分析-充电宝台灯 ④电子产品拆解分析-太阳能自动感应灯 ⑤电子产品拆解分析-人体感应灯 ⑥电子产品拆解分析-食物电子秤 ⑦电子产品拆解分析-6600mA充电宝 ⑨电子产品拆解分析-触摸化妆镜…...
Tkinter 一文读懂
Tkinter 简介 Tkinter(即 tk interface,简称“Tk”)本质上是对 Tcl/Tk 软件包的 Python 接口封装,它是 Python 官方推荐的 GUI 工具包,属于 Python 自带的标准库模块,当您安装好 Python 后,就可…...
2核4G服务器阿里云性能测评和优惠价格表
阿里云2核4G服务器租用优惠价格,轻量2核4G服务器165元一年、u1服务器2核4G5M带宽199元一年、云服务器e实例30元3个月,活动链接 aliyunfuwuqi.com/go/aliyun 活动链接如下图: 阿里云2核4G服务器优惠价格 轻量应用服务器2核2G4M带宽、60GB高效…...
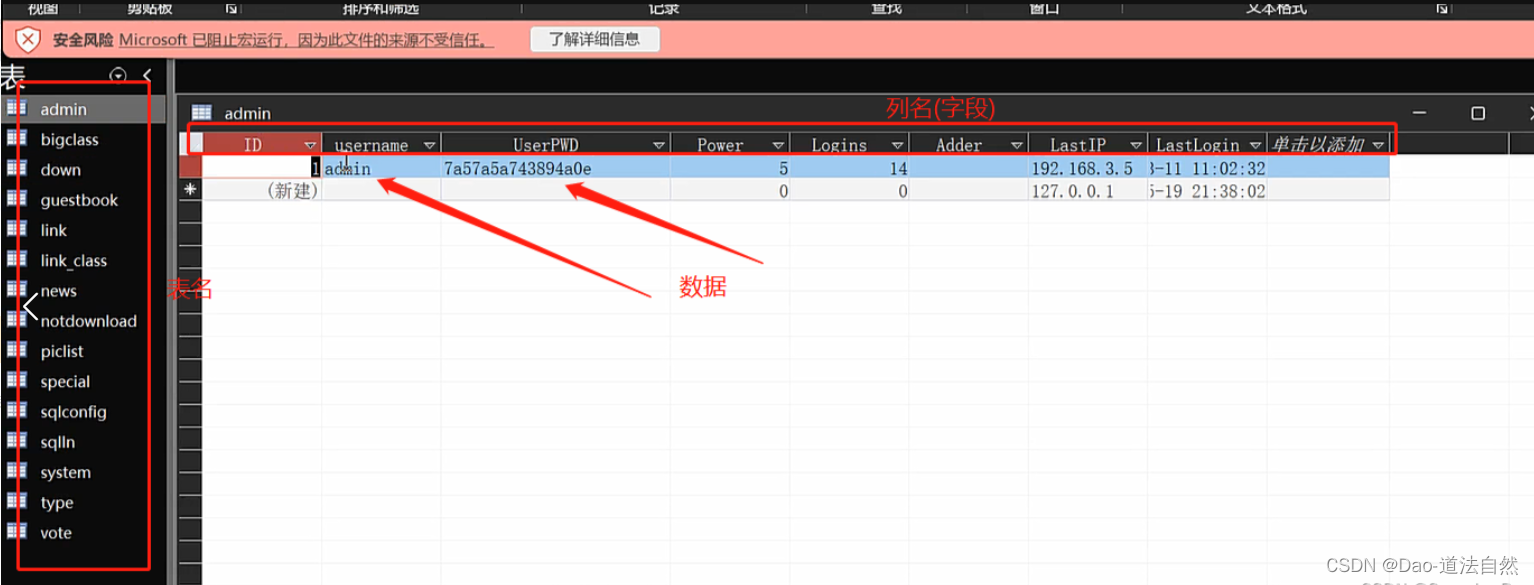
Day41:WEB攻防-ASP应用HTTP.SYS短文件文件解析Access注入数据库泄漏
目录 ASP-默认安装-MDB数据库泄漏下载 ASP-中间件-CVE&短文件&解析&写权限 HTTP.SYS(CVE-2015-1635)主要用作蓝屏破坏,跟权限不挂钩 IIS短文件(iis全版本都可能有这个问题) IIS文件解析 IIS写权限 ASP-SQL注入-SQLMAP使用…...
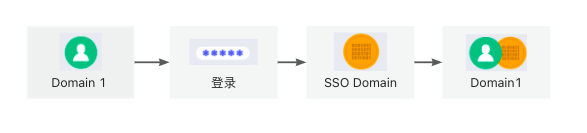
什么是单点登录?
单点登录(Single Sign On,简称 SSO)简单来说就是用户只需在一处登录,不用在其他多系统环境下重复登录。用户的一次登录就能得到其他所有系统的信任。 为什么需要单点登录 单点登录在大型网站应用频繁,比如阿里旗下有淘…...
elasticsearch的数据搜索
DSL查询文档 elasticsearch的查询依然是基于JSON风格的DSL来实现的。 Elasticsearch提供了基于JSON的DSL(Domain Specific Language)来定义查询。常见的查询类型包括: 查询所有:查询出所有数据,一般测试用。例如:match_all 全文检索(full text)查询:利用分词器对用户…...
)
云原生相关概念(小白版)
先说概念: 云原生应该是一种“建立在云上的多种效率提升技术的复合体"(而不是单一的技术创新),主要就是在云技术摆脱物理储存限制的基础上,进一步实现应用的专业优化(即文章里说的按功能切分…...
Dell戴尔XPS 12 9250二合一笔记本电脑原装出厂Windows10系统包下载
链接:https://pan.baidu.com/s/1rqUEM_q5DznF0om6eevcwg?pwdvij0 提取码:vij0 戴尔原厂WIN10系统自带所有驱动、出厂主题壁纸、系统属性专属联机支持标志、系统属性专属LOGO标志、Office办公软件、MyDell等预装程序 文件格式:esd/wim/sw…...

YOLOv5改进 | 图像去雾 | 利用图像去雾网络AOD-PONO-Net网络增改进图像物体检测(全网独家首发)
一、本文介绍 本文给大家带来的改进机制是利用AODNet图像去雾网络结合PONO机制实现二次增强,我将该网络结合YOLOv5针对图像进行去雾检测(也适用于一些模糊场景,图片不清晰的检测),同时本文的内容不影响其它的模块改进可以作为工作量凑近大家的论文里,非常的适用,图像去…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
