Android 12.0 通过驱动实现禁用usb鼠标和usb键盘功能
1.1概述
在12.0的系统产品定制化开发中,在进行定制中有关于usb键盘和usb鼠标的需求中,产品要求禁止usb口挂载usb鼠标和usb键盘,所以需要要求在usb挂载类型的时候
判断如果是usb鼠标和usb键盘就不让挂载,这就需要从驱动方面入手来解决这个问题,接下来看下驱动的某些挂载usb的相关文件来解决这个功能的禁用问题
2.1通过驱动实现禁用usb鼠标和usb键盘功能的核心类
kernel-4.14\drivers\hid\hid-core.c
kernel-4.14\drivers\hid\usbhid\hid-core.c3.通过驱动实现禁用usb鼠标和usb键盘功能的核心功能分析和实现
在android 系统中usb鼠标和usb键盘都属于input输入设备,而在linux中常用的drivers/hid/usbhid/usbmouse.c驱动
作为usb鼠标的驱动,而在android系统中10.0以前是使用drivers/hid/usbhid/usbmouse.c作为usb鼠标驱动而在12.0没有使用drivers/hid/usbhid/usbmouse.c作为usb鼠标驱动,
而是使用了hid-generic驱动,两个主要的文件就是hid-core.c文件,分别为hid/hid-core.c和hid/usbhid/hid-core.c文件。
前者注册hid总线,后者注册hid device,综合上述分析主要是在usbhid/hid-core.c中实现usb设备挂载,接下来看下hid-core.c
相关文章:

Android 12.0 通过驱动实现禁用usb鼠标和usb键盘功能
1.1概述 在12.0的系统产品定制化开发中,在进行定制中有关于usb键盘和usb鼠标的需求中,产品要求禁止usb口挂载usb鼠标和usb键盘,所以需要要求在usb挂载类型的时候 判断如果是usb鼠标和usb键盘就不让挂载,这就需要从驱动方面入手来解决这个问题,接下来看下驱动的某些挂载usb…...
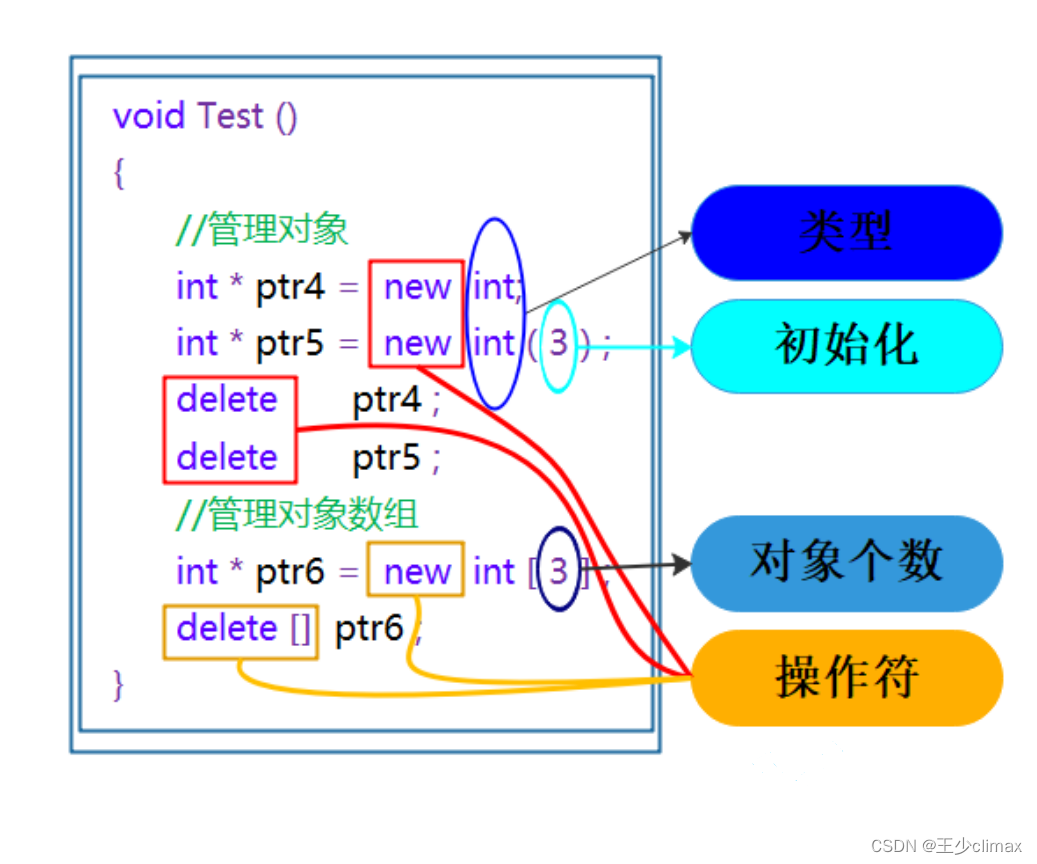
C++入门——内存管理
C入门——内存管理 C/C内存分布 分类是为了更好的管理 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] {1, 2, 3, 4};char char2[] "abcd";char* pChar3 "abcd";int* ptr1 (…...
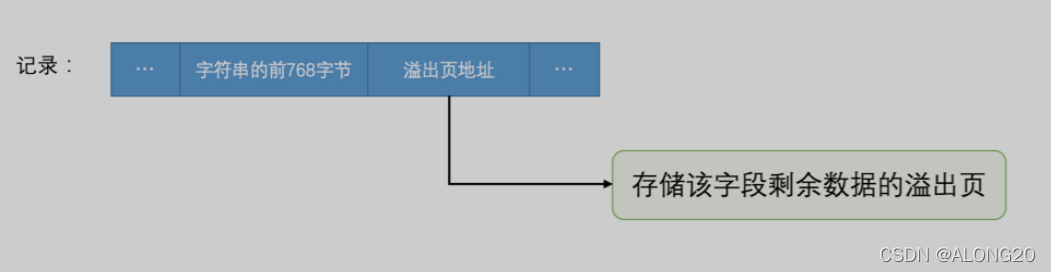
MySQL-InnoDB行格式浅析
简介 我们知道读写磁盘的速度非常慢,和内存读写差了几个数量级,所以当我们想从表中获取某些记录时, InnoDB 存储引擎需要一条一条的把记录从磁盘上读出来么? 不,那样会慢死,InnoDB 采取的方式是:…...
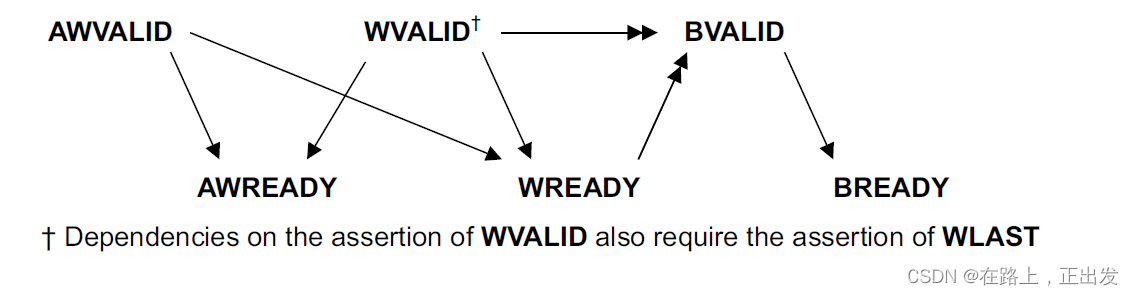
AXI 总线协议学习笔记(4)
引言 前面两篇博文从简单介绍的角度说明了 AXI协议规范。 AXI 总线协议学习笔记(2) AXI 总线协议学习笔记(3) 从本篇开始,详细翻译并学习AXI协议的官方发布规范。 文档中的时序图说明: AXI指࿱…...

C++复习笔记6
1.String类的实现 注意深浅拷贝, C语言字符串拼接函数strcat() #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<vld.h> #include<assert.h> using namespace std;class String {friend ostream& operator<<(ostream &am…...
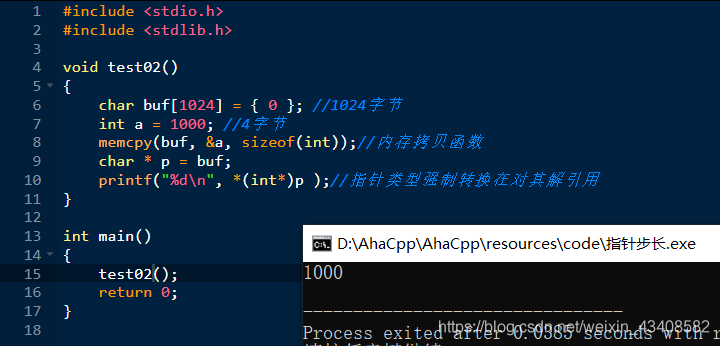
指针的步长及意义(C语言基础)
指针的步长及意义 文章目录指针的步长及意义指针变量1后偏移的字节数不同指针解引用时取出的字节数不同其他例子不同类型的指针有何不同的意义指针变量1后跳跃字节数量不同解引用的时候,取出字节数量不同 指针变量1后偏移的字节数不同 代码演示:&#…...
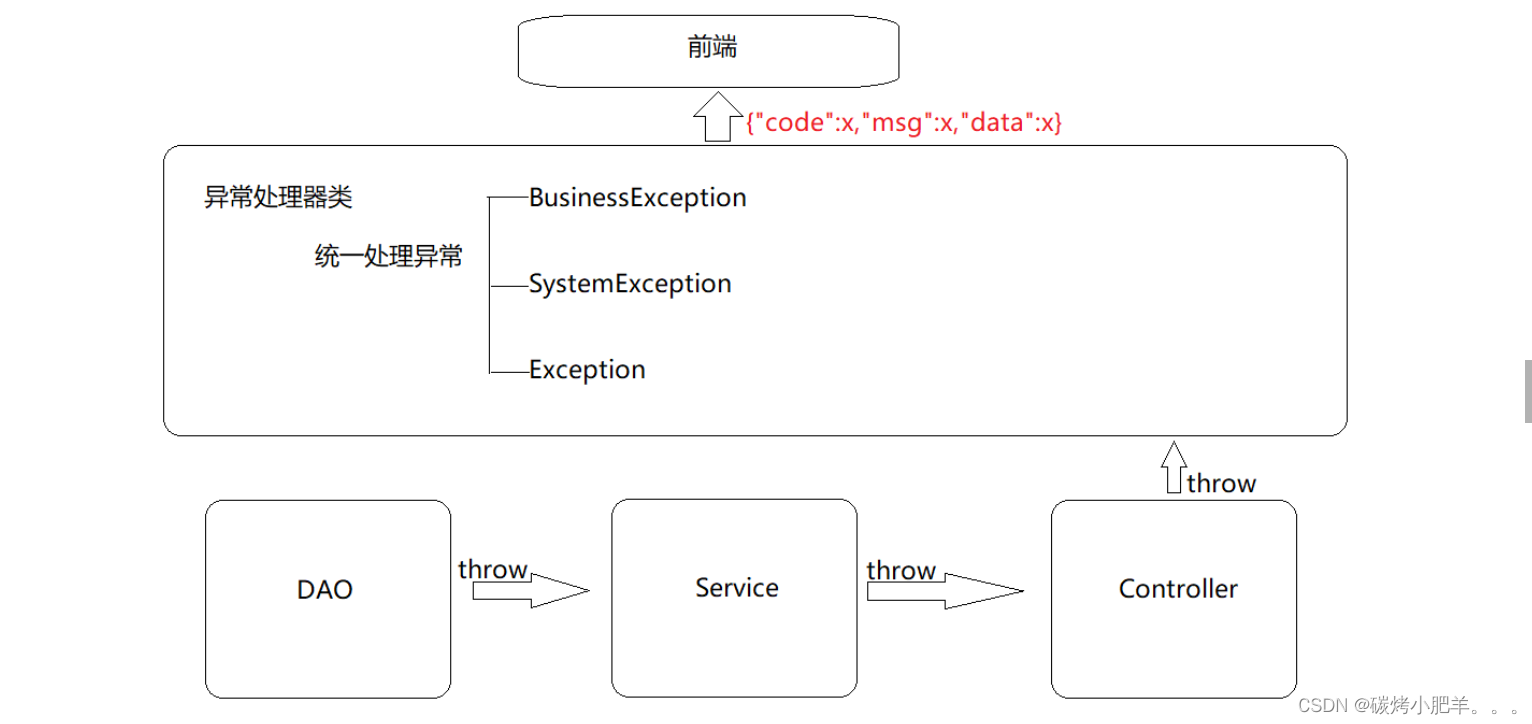
SpringMVC:统一异常处理(11)
统一异常处理1. 说明2. 问题描述3. 异常处理器使用3.1 创建异常处理器类3.2 让程序抛出异常3.3 测试4. 项目异常处理方案4.1 异常分类4.2 异常解决方案4.3 异常解决方案的具体实现4.4 测试5. 总结1. 说明 \quad本篇文章是在文章SpringMVC:SSM整合(Spring…...
SpringBoot的配置与使用
SpringBoot简介 我们的Spring是包含了众多工具的IoC容器,而SpringBoot则是Spring的加强版,可以更加方便快捷的使用 如果Spring是手动挡的车,那么SpringBoot就是自动挡的车,让我们的驾驶体验变得更好 SpringBoot具有一下几种特征…...
【Python】tkinter messagebox练习笔记
我一好友在朋友圈看到人家用代码花式秀恩爱,让我也做一个,我就用我学习半年python的功力,做了这一个东西。🙏窗口主页面(图一)为了让我这个盆友有颜面,特意做了一个问答问他帅不帅,以…...
答案解析)
2022年12月电子学会Python等级考试试卷(五级)答案解析
青少年软件编程(Python)等级考试试卷(五级) 分数:100 题数:38 一、单选题(共25题,共50分) 1. 下面哪个语句正确定义了元组类型数据tuple1?( ) A. t…...
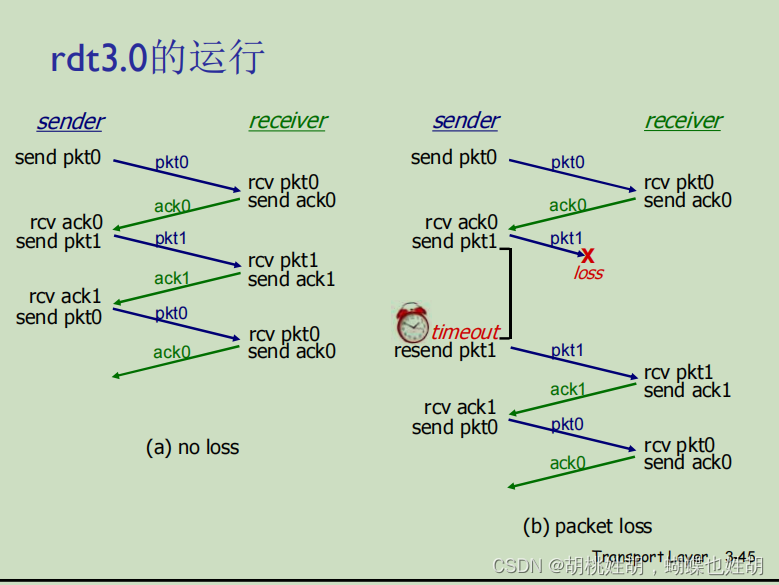
计算机网络自定向下 -- 浅谈可靠性之rdt协议
可靠性数据传输原理 可靠指数据在传输过程中不错,不丢,不乱 运输层要为应用层提供一种服务:数据可以通过一条可靠的信道进行传输,在该信道中传输的数据不会受到损坏或者丢失, 实现这种服务的是可靠数据传输协议。 要实现这种服…...
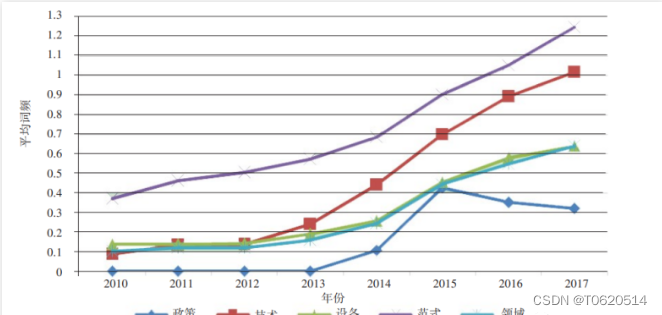
制造业升级转型:制造业上市公司-智能制造词频统计数据集
发展智能制造,关乎中国制造业转型升级的成效。基于中国制造业上市公司年报,通过文本数据挖掘,提取关键词反映企业对智能制造的关切焦点,进而运用词频及共词网络分析,洞察中国智能制造的发展态势。 研究发现࿰…...

HTML 开发工具整理
一、千乐微云团队推荐的HTML开发工具Visual Studio Code 简称VS Code (第一推荐)Visual Studio Code (简称 VS Code / VSC) 是一款免费开源的现代化轻量级代码编辑器,支持几乎所有主流的开发语言的语法高亮、智能代码补全、自定义快捷键、括号…...

介绍ACE C++网络通信框架
很久以前笔者也不太熟悉ACE C网络通信框架,偶然的机会逐渐接触后,发现它的优良! 总结来看它的有点如下 非常适合后台无界面网络通信的系统编程 适合小型化核心网使用;但值得注意,如果您需要的是web领域技术栈&…...
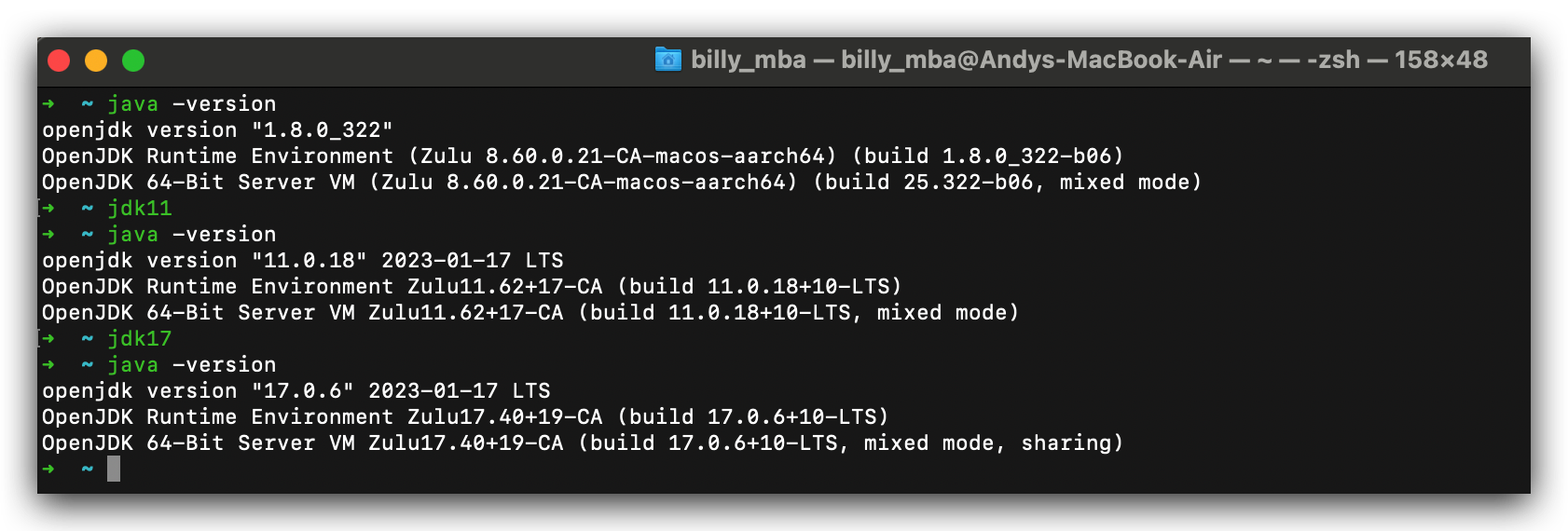
【Mac OS】JDK 多版本切换配置
前言 由于不同的项目可能需要使用的 JDK 版本不一样,所以在系统中配置多个 JDK 版本,并且能随时切换,是一个必要的配置。 查看已安装的 JDK 版本 /usr/libexec/java_home -V框框1是执行的命令 框框2是当前系统下所有的 JDK 版本 框框3是当…...
RabbitMQ-Exchanges交换机
一、介绍 RabbitMQ消息传递模型的核心思想是:生产者生产的消息从不会直接发送到队列。实际上,通常生产者甚至不知道这些消息传递到了哪些队列中。相反,生产者只能将消息发送到交换机,交换机工作的内容非常简单,一方…...

离散数学 课时二 命题逻辑等值演算
等值式(等值联结词) 1、设A、B是两个命题公式,若A、B构成的等价式 A等价于B 为重言式,那么称A与B是等值的 2、常用等值式: 注意: 1 双否定律 2 幂等律 3 交换律 4 结合律 5 吸收律 6 德摩根律 7 同一律 8 零律 9 矛盾律 10 排中律 11 蕴含表达式 12 …...

Debezium系列之:事件扁平化转换SMT,简化debezium数据格式,为数据添加head,为值添加键值对
Debezium系列之:事件扁平化转换SMT,简化debezium数据格式,为数据添加head,为值添加键值对 一、需求背景二、Debezium数据格式和扁平化数据格式对比三、事件扁平化SMT作用四、事件扁平化转换SMT设置五、事件扁平化参数详解六、完整SMT参数配置一、需求背景 Debezium 数据更改…...
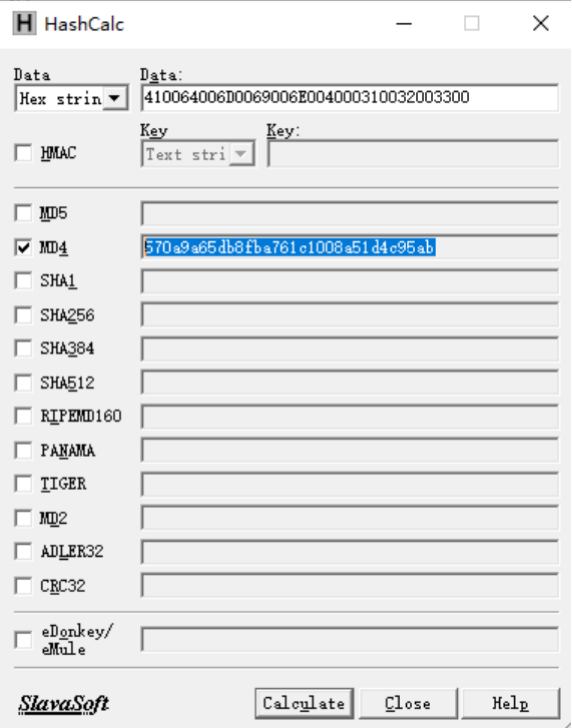
内网渗透(十八)之Windows协议认证和密码抓取-本地认证(NTML哈希和LM哈希)
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...
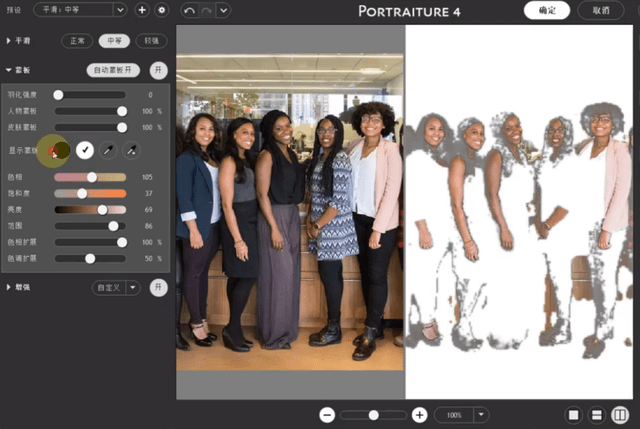
Portraiture全新4.0最新版人像磨皮插件更新内容
Portraiture是一款智能磨皮插件,为Photoshop和Lightroom添加一键磨皮美化功能,快速对照片中皮肤、头发、眉毛等部位进行美化,无需手动调整,大大提高P图效率。全新4版本,升级AI算法,并独家支持多人及全身模式…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
