MATLAB的使用(一)
一,MATLAB的编程特点
a,语法高度简化;
b,脚本式解释型语言;
c,针对矩阵的高性能运算;
d,丰富的函数工具箱支持;
e,通过matlab本体构建跨平台;
二,MATLAB的界面

工具栏:提供快捷操作编辑器:
脚本代码窗口工作区:
脚本变量窗口工作路径:
当前文件运行的检索路径
三,MATLAB的工具栏
新建脚本:新建脚本或函数(*.m)文件
新建实时脚本:新建可交互脚本(*.mlx)文件
新建/打卡:支持更加泛化的新建/打开文件类型导入数据:加载可识别的数据文件
保存工作区:将工作区的文件保存至(*.mat)文件
Simulink:打开可视化仿真工具
预设:MATLAB相关参数设置
帮助:查询相关文档和示例
四,常用控制代码
4.1 clc:清空命令行


4.2 clear:清空工作区变量


4.3 clear all:清空工作区(在一般matlab使用中等价于clear)
4.4 close:关闭当前图像窗口
4.5 *dbstop if error:建立变量缓冲区,在错误位置自动断点调试
编译器会报错,在错误的地方停止运行

4.6 Crtl + R/crtl + T:注释和反注释(支持批量)
4.7 ctrl + C: 强制停止
4.8 crtl + R:智能缩进
4.9 F9:在命令行中运行编译器内代码
五,MATLAB运算
命令行==计算器?
1,加+ 减- 乘* 除 /

2,平方根 sqrt(),任意次幂()^();power(,)

4,对数 log();log10();log2(); log1p()

5,指数exp();expm1();pow2();nextpow2()

6,三角函数 sin( );cos(); sinpi( );cospi();tan( )

7,反三角函数 asin( );acos( );asind();acosd( );atan( );atand( ); atan2()

六,MATLAB整体运算
1 模与余数 mod(,)rem(,)

2,符号函数sign()

3,matlab小数计算

4,matlab整体运算

5,生成随机数
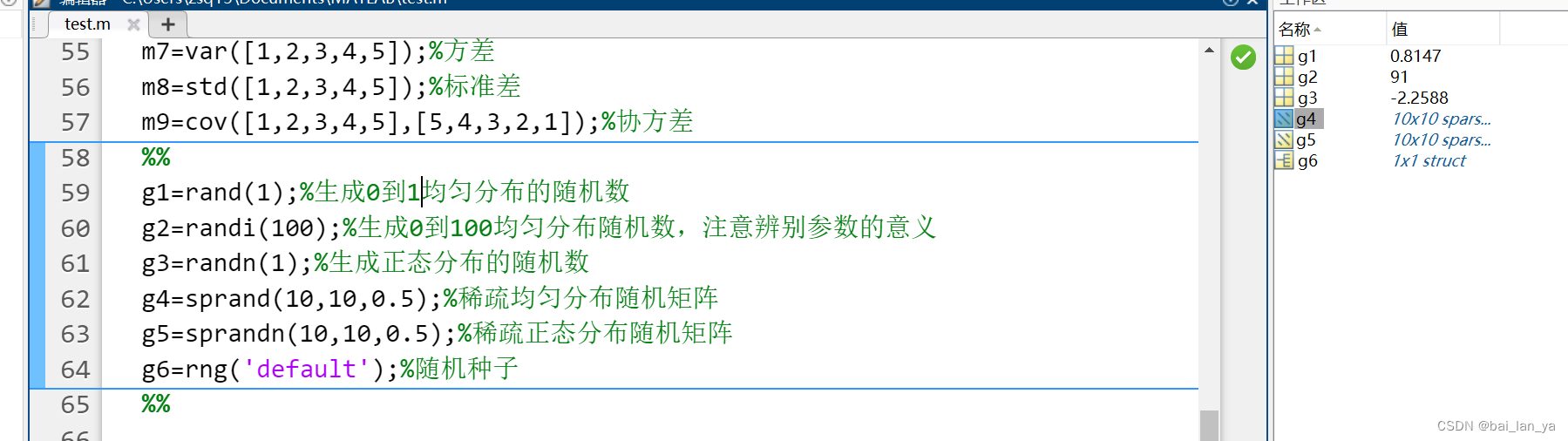
七,矩阵
1,矩阵的重要性
矩阵是MATLAB的核心
MATLAB通过建立特定平台进行大量的硬件针对性优化
2,创建向量
特殊的矩阵形式:向量。
生成格式:
①起始数据:数据间隔(可忽略,默认为1):结束数据
示例:
1:100(等价于1:1:100) 范围为1到100,间隔为1,1*100的向量
1:2:100 范围为1到100,间隔为2,1*50的向量
100:-1:1 范围为1到100,间隔为-1,1*100的向量
1:1:100.7 范围为1到100(<=100.7的最大整数),间隔为1,1*100的向量
②特殊异常模式(三冒号表达式)A:B:C:D
>>1:2:4:5 >>2:-1:3:5
ans = ans =
1 2 3 4 5 空的 1*0 的double行向量
无用形式,但不会报错
3,赋值方法
[3.4] 创建了值为3.4的1乘1矩阵(标量)
[1.0,2.0,3.0] 创建了值为[1 2 3]的1乘3矩阵(行向量)
[1.0 2.0 3.0] 创建了值为[1 2 3]的1乘3矩阵(行向量)
[1.0; 2.0; 3.0] 创建了值为[1 2 3]^T的3乘1矩阵(列向量)
[1,2, 3; 4, 5, 6] 创建了值为2*3的矩阵
[1,2,3
4, 5,6] 创建了值为2*3的矩阵
采用逗号或空格来分割行元素
采用分号或换行来分割列元素
4,矩阵快速创建方法


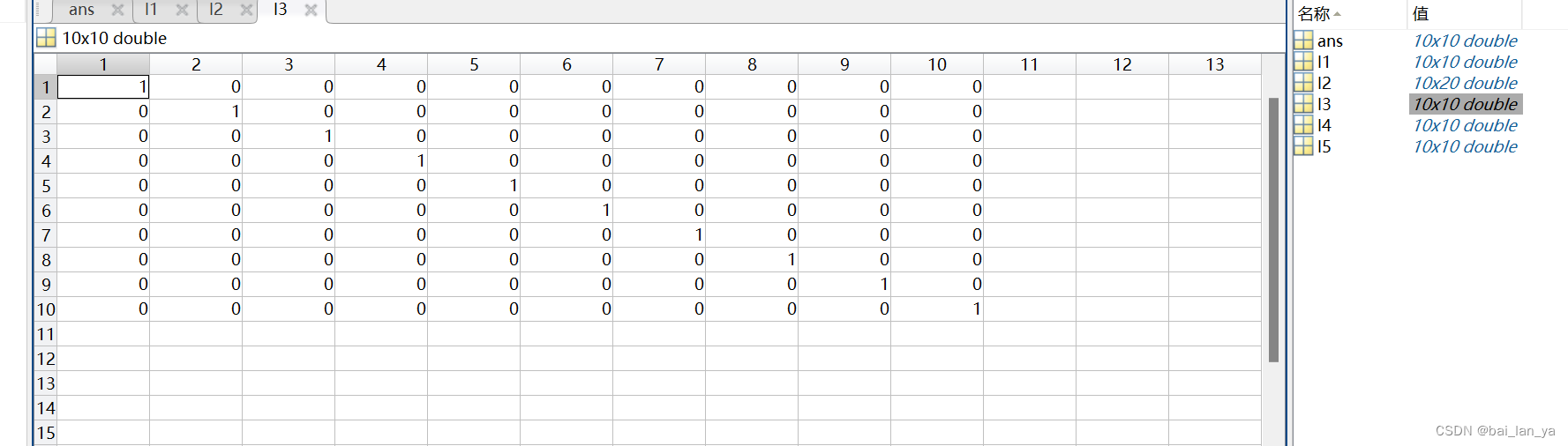
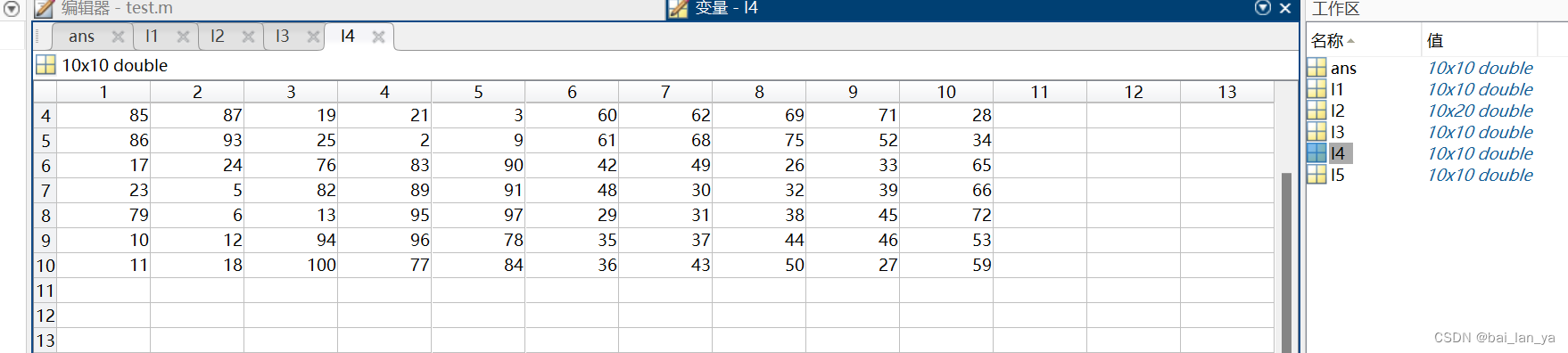


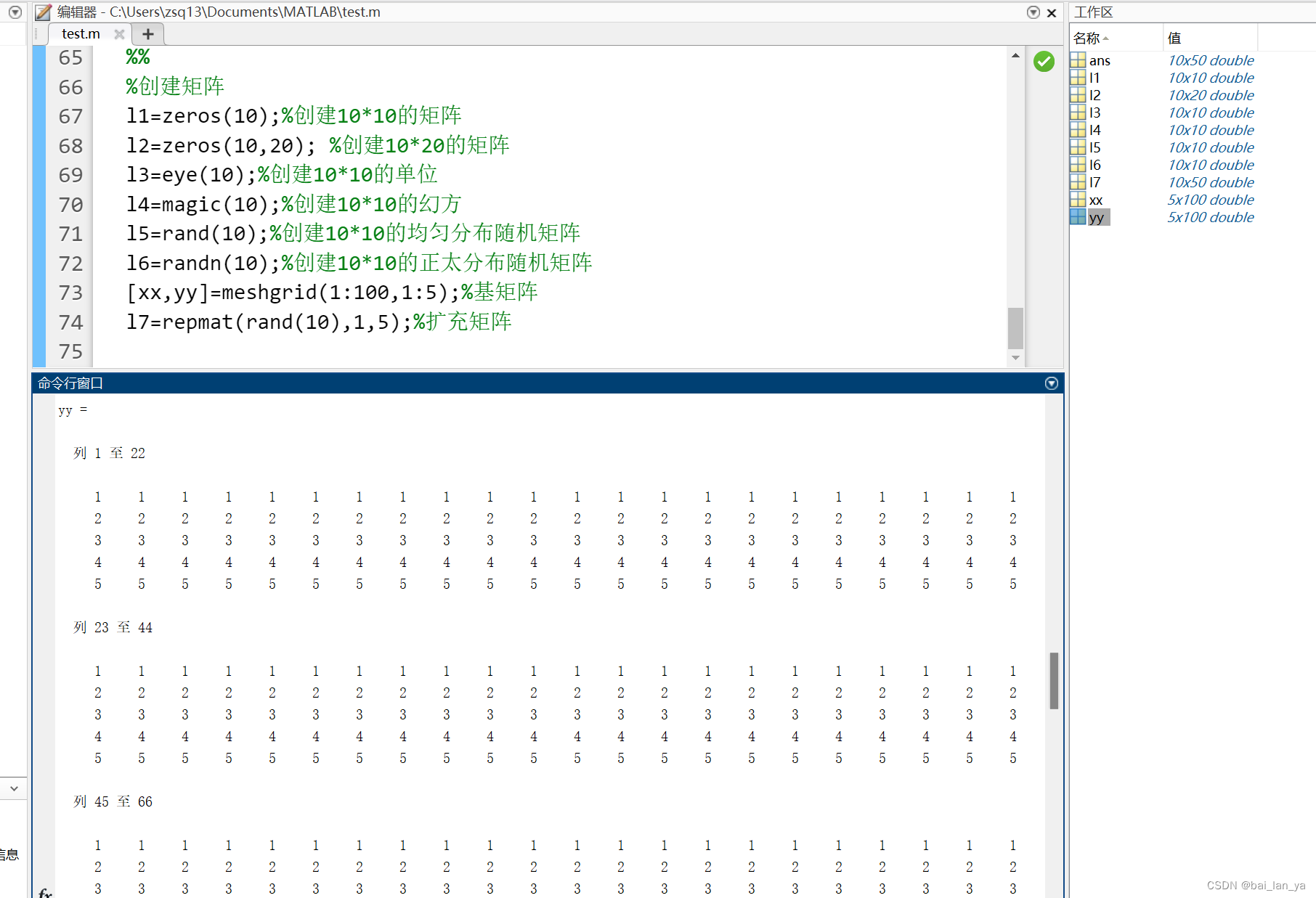
5,矩阵运算模式
矩阵相乘 A*B
矩阵右乘 A/B等价于A*B的逆 注意左除和右除的区别
矩阵左乘 A/B等价于A的逆乘B
矩阵数乘 A.*B
矩阵右除 A./B等价于A除以B 每个元素进行分别操作
矩阵左除 A./B等价于A除B
对于数+/-矩阵,其相当于在矩阵每个元素加减此数

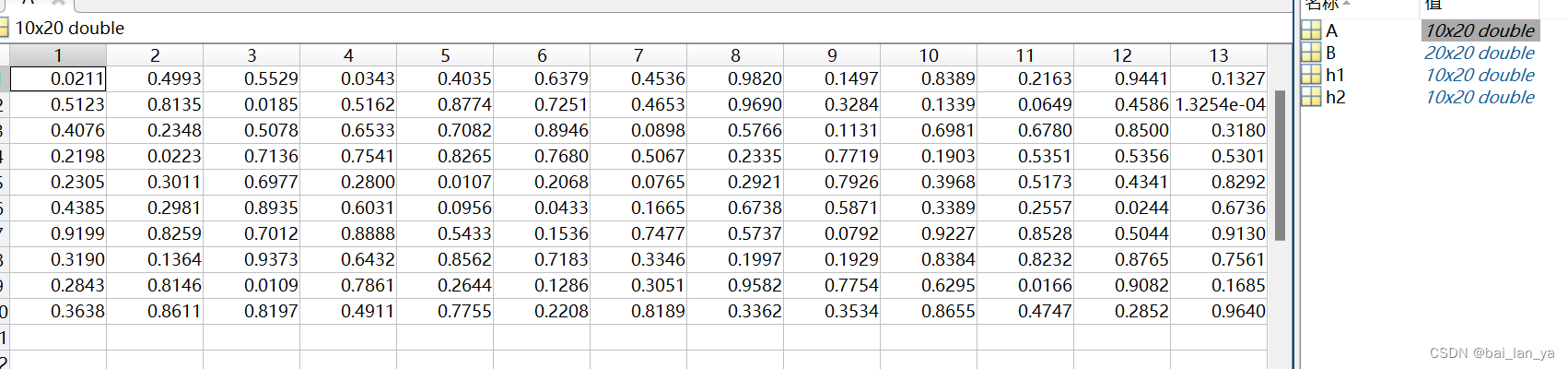


 6,其他运算方法
6,其他运算方法
矩阵A求逆 inv(A)
矩阵A求伪逆 pinv(A) 适用于非方阵和奇异阵
矩阵A求转置 A'
求行列式A det(A)
求行列式A的迹 trace(A)
求矩阵A的LU分解 lu(A)
求矩阵A的QR分解 qr(A)
求矩阵A的特征值与向量 eig(A) 矩阵分析常用

大家可以自己打代码试一下
7,矩阵数据的提取
确定矩阵的大小
length()-用于向量 size()-用于矩阵
元素提取:
A(m,n)表示提取矩阵的第m,n位置处的值
注意m,n不能超出矩阵维度,matlab中起始值为1
冒号/end提取法:
A( :1) 提取矩阵第一列
A(1,: ) 提取矩阵第一行
A(1,end) 提取矩阵第一行中最后一个值
A(2:2:end,:) 提取偶数行
8,矩阵操作
-更改矩阵的大小:
Matrix_out = reshape( Matrix_in , m , n)
m/n为新矩阵的行数和列数
注意在矩阵改变的同时不能改变元素个数
-复制扩充:
Matrix out = repmat( Matrix_in , m , n)
m/n为扩充的行倍数和列倍数
9,交叉知识-稀疏矩阵
采用[(m,n),value]三元组来存储数据,不存储0值以节省空间
直接生成稀疏矩阵:sparse(m,n)
将矩阵A强制转化为稀疏矩阵:sparse(A)
>>one(1e5)
错误使用 ones
请求的100000*100000(74.5GB)数组超过预设的最大数值大小
>>sparse(1e5,1e5)
ans=
全零稀疏矩阵:100000*100000
节省存储空间,对于严重稀疏矩阵加快运算速度
八,逻辑
1,逻辑变量
Logical类型:true(真值),false(假值)
>>a = true
a =
logical
1
*******************************************
>>b=false
b=
logical
0
*******************************************
>>a = true + 1.1
a =
2.1000
*******************************************
逻辑变量可参与运算,参与运算时其默认值为1/0
>>logical(-0.5)
ans=
logical
1
*****************************************************
>>logical(2)
ans=
logical
2
*******************************************************
逻辑类型的强制中,所有非0值(包括字符串)都会转化为真值
2,逻辑判定

3,逻辑运算

4,优先级
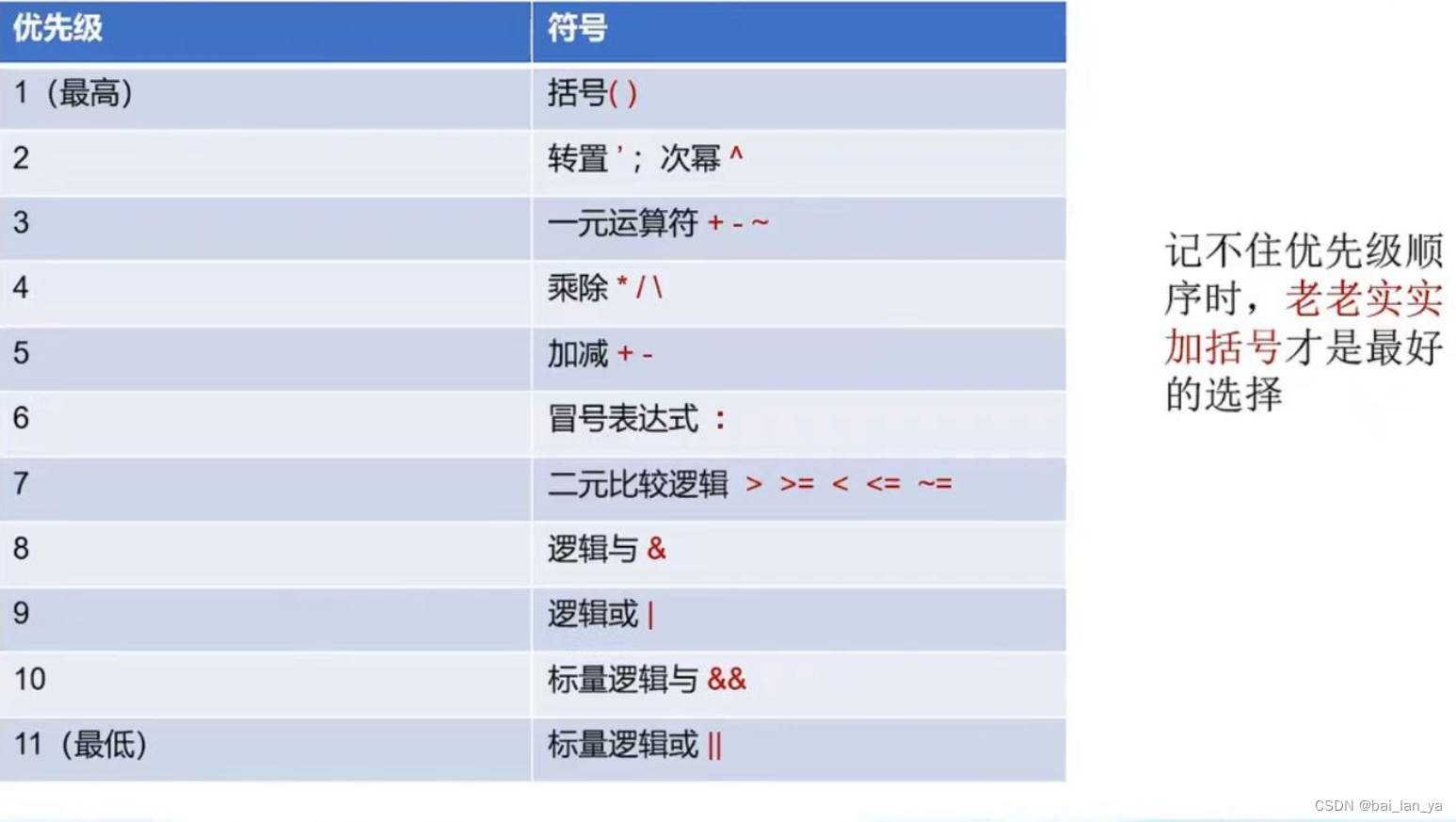
相关文章:

MATLAB的使用(一)
一,MATLAB的编程特点 a,语法高度简化; b,脚本式解释型语言; c,针对矩阵的高性能运算; d,丰富的函数工具箱支持; e,通过matlab本体构建跨平台; 二,MATLAB的界面 工具栏:提供快捷操作编辑器…...

JMeter并发工具的使用
视频地址:Jmeter安装教程01_Jmeter之安装以及环境变量配置_哔哩哔哩_bilibili 一、JMeter是什么 JMeter是一款免安装包,官网下载好后直接解压缩并配置好环境变量就可以使用。 环境变量配置可参考:https://www.cnblogs.com/liulinghua90/p/…...
基于springboot+vue的毕业就业信息管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

有什么小程序适合个人开发?
在这个信息爆炸的时代,小程序已经成为了我们生活中的一部分。无论是出行、购物还是娱乐,小程序都能为我们提供便捷的服务。对于个人开发者来说,开发一个小程序不仅可以锻炼自己的技术能力,还可以为他人提供便利,甚至有…...
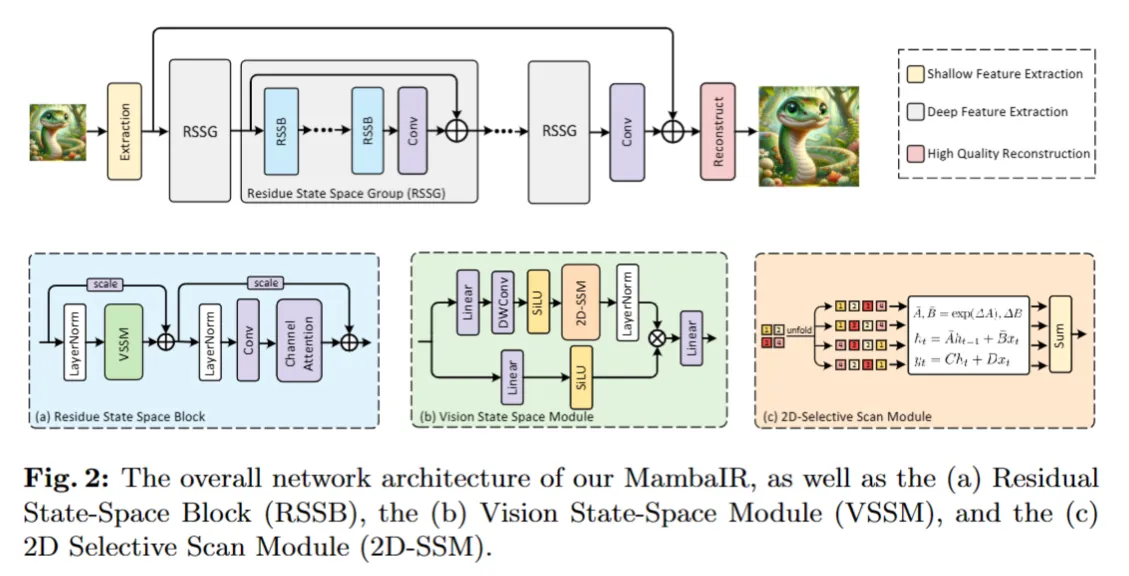
【ARXIV2402】MambaIR
这个工作首次将 Mamba 引入到图像修复任务,关于为什么 Mamba 可以用于图像修复,作者有非常详细的解释:一路向北:性能超越SwinIR!MambaIR: 基于Mamba的图像复原基准模型 作者认为Mamba可以理解为RNN和CNN的结合…...

【计算机网络篇】数据链路层(3)差错检测
文章目录 🥚误码🍔两种常见的检错技术⭐奇偶校验⭐循环冗余校验🎈例子 🥚误码 误码首先介绍误码的相关概念 🍔两种常见的检错技术 ⭐奇偶校验 奇校验是在待发送的数据后面添加1个校验位,使得添加该校验…...

软件配置管理计划
1. 配置管理目标 本软件配置管理计划的目标在于确保软件开发生命周期内的所有配置项(CI)都得到适当的标识、控制、版本管理和追踪。通过实施有效的配置管理,我们的目标是: 保持配置项的一致性和完整性。确保配置项的可追溯性。减…...

嵌入式备考错题汇总
若某条无条件转移汇编指令采用直接寻址,则该指令的功能是将指令中的地址码送入()。 A.PC(程序计数器) B.AR(地址寄存器) C.AC(累加器) D.ALU(算术逻辑运算单元) 解析:选A,直接寻址是指操作数存放在内存单元中,指令中直接给出操作数所在存储单…...

38 mars3d 对接地图图层 绘制点线面员
前言 这里主要是展示一下 mars3d 的一个基础的使用 主要是设计 接入地图服务器的 卫星地图, 普通的二维地图, 增加地区标记 基础绘制 点线面园 等等 测试用例 <template><div style"width: 1920px; height:1080px;"><div class"mars3dClas…...

什么是Webhook 和 HTTP Endpoint?
Webhook 和 HTTP Endpoint 都是基于HTTP协议的网络通信概念,但它们在使用场景和目的上有所不同。 Webhook Webhook 是一种允许一个应用程序提供实时信息给其他应用程序的方法,这种通信是基于HTTP的“回调”或“钩子”。Webhook 通常被用来在一种服务上…...

小程序跨端组件库 Mpx-cube-ui 开源:助力高效业务开发与主题定制
Mpx-cube-ui 是一款基于 Mpx 小程序框架的移动端基础组件库,一份源码可以跨端输出所有小程序平台及 Web,同时具备良好的拓展能力和可定制化的能力来帮助你快速构建 Mpx 应用项目。 Mpx-cube-ui 提供了灵活配置的主题定制能力,在组件设计开发阶…...

GDC期间LayaAir启动全球化战略
3 月 18 日至 3 月 22 日,一年一度的游戏开发者大会(GDC)在美国旧金山举行。在此期间,Layabox宣布LayaAir引擎启动全球扩张战略,这标志着引擎将步入快速发展的新阶段。此举旨在利用公司先进的3D引擎技术,将…...
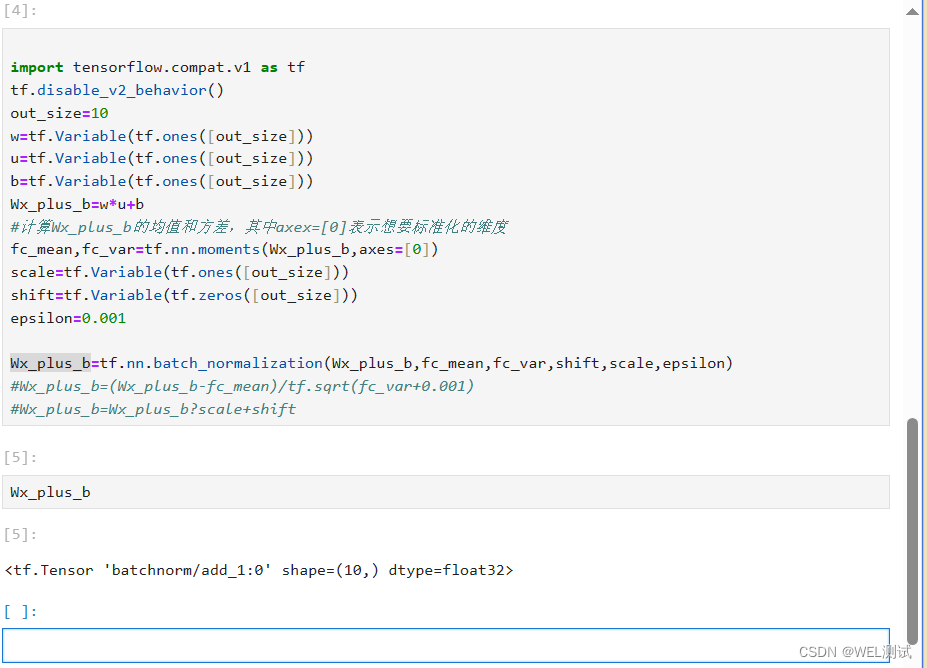
人工智能之Tensorflow批标准化
批标准化(Batch Normalization,BN)是为了克服神经网络层数加深导致难以训练而诞生的。 随着神经网络的深度加深,训练会越来越困难,收敛速度会很慢,常常会导致梯度消失问题。梯度消失问题是在神经网络中,当前…...
自动化的免下车服务——银行、餐厅、快餐店、杂货店
如果您在20世纪70年代和2020年分别驾车经过免下车服务餐厅(汽车穿梭餐厅),您会发现,唯一的不同是排队的车型。50多年来,免下车技术一直为我们提供着良好的服务,但现在也该对它进行现代化改造了。 乘着AI和自…...

Git常用指令总结
Git常用指令总结 下载git,这个不需要交的!!! 1、初始化自己的git仓库 git config --global user.name “Your name” 配置自己的用户名 git config --global user.email “mailexample.com” 配置邮箱 git config --global c…...
水果软件FL Studio 21 for mac 21.2.3.3586破解版的最新版本2024介绍安装
音乐是人类最美好的语言,它能够跨越国界、文化和语言,将人们紧密地联系在一起。在当今数字化时代,音乐创作已经不再是专业人士的专利,越来越多的音乐爱好者开始尝试自己动手制作音乐。而FL Studio21中文版编曲软件正是这样一个为你…...

【保姆级】前端使用node.js基础教程
文章目录 安装和版本管理:npm 命令(Node 包管理器):运行 Node.js 脚本:调试和开发工具:其他常用命令:模块管理:包管理:调试工具:异步编程和包管理:…...
xilinx的高速接口构成原理和连接结构
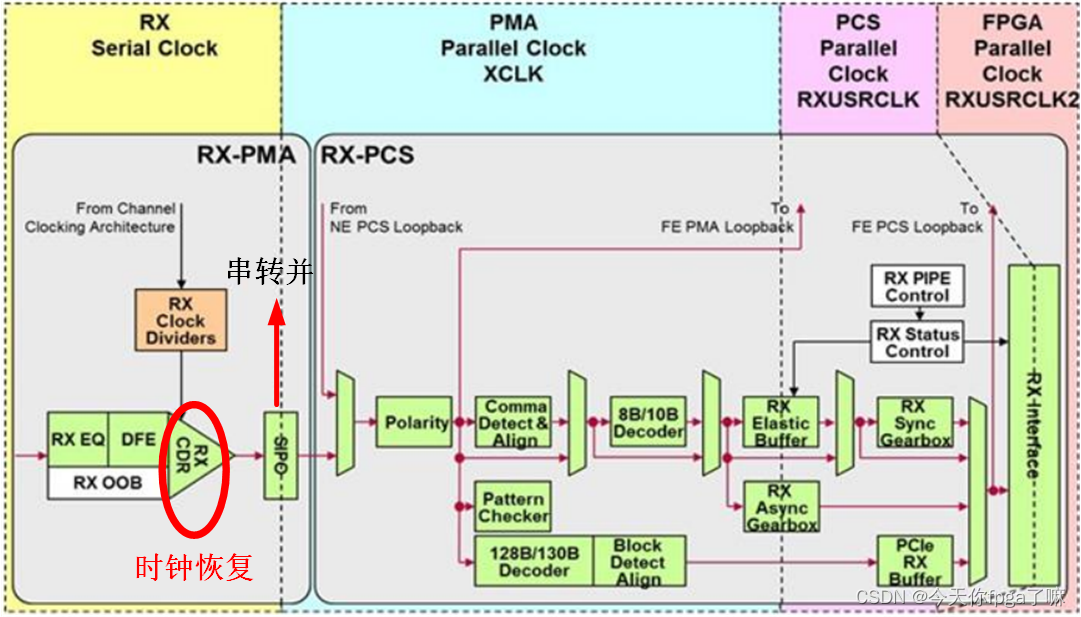
本文来源: V3学院 尤老师的培训班笔记【高速收发器】xilinx高速收发器学习记录Xilinx-7Series-FPGA高速收发器使用学习—概述与参考时钟GT Transceiver的总体架构梳理 文章目录 一、概述:二、高速收发器结构:2.1 QUAD2.1.1 时钟2.1.2 CHANNEL…...
git 上传文件夹至远端仓库的方法
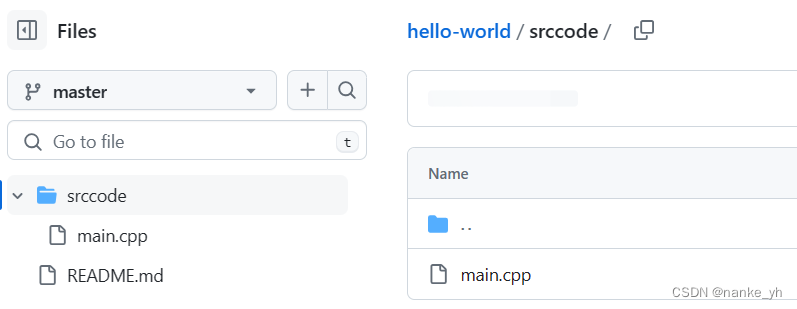
上传的远端git可以是gitlab、github、gitee、gitblit或者gitCode等等 以下以GitHub为例说明: 1、登录GitHub网站(账户/密码) 2、创建一个新的空白项目(或者已有的项目)hello-world 分支是master ,这里默认即…...

【鸿蒙系统】 ---OpenHarmony加快本地编译(二)
💌 所属专栏:【鸿蒙系统】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
