【MATLAB源码-第168期】基于matlab的布谷鸟优化算法(COA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境:
MATLAB 2022a
1、算法描述
布谷鸟优化算法(Cuckoo Optimization Algorithm, COA)是一种启发式搜索算法,其设计灵感源自于布谷鸟的独特生活习性,尤其是它们的寄生繁殖行为。该算法通过模拟布谷鸟在自然界中的行为特点,为解决各种复杂的优化问题提供了一种新颖的方法。从算法提出至今,COA因其高效性和简洁性,在全球科研界和工业界引起了广泛的关注和应用。以下是对布谷鸟优化算法的详细介绍,包括其背景、原理、操作步骤、特性及应用范围等方面的全面阐述。
1. 算法背景与启发源泉
在自然界中,布谷鸟是一类非常有趣的鸟类,它们并不自己筑巢,而是将自己的蛋寄生在其他鸟类的巢中,由其他鸟类代为孵化和养育。这种独特的生殖策略使得布谷鸟能够将更多的能量用于生产蛋,而不是花费在养育后代上。此外,布谷鸟的蛋通常会首先孵化,其幼鸟会将宿主鸟的蛋或幼鸟挤出巢外,以获得更多的养育资源。这种自然现象在生物学上称为“寄生养育”(Brood Parasitism)。
算法的设计者由此得到启发,将布谷鸟的这种寄生繁殖行为抽象为一种优化策略,用于寻找问题的最优解。在这一策略中,每一个布谷鸟的蛋代表了问题的一个潜在解,而巢则代表了解的空间或环境。
2. 算法原理与核心步骤
布谷鸟优化算法的核心在于模拟布谷鸟的寄生繁殖策略和迁徙行为,通过以下几个关键步骤来实现:
(a) 初始群体生成
算法初始化时,首先随机生成一组布谷鸟群体,每只布谷鸟代表一个潜在的解。
(b) 寄生繁殖与蛋的产生
在每一代中,算法通过随机选择布谷鸟并产生新的蛋(即解)来模拟布谷鸟的寄生繁殖过程。新产生的蛋将替换掉在解空间中随机选择的其他蛋,模拟了布谷鸟蛋的寄生特性。
(c) 蛋的发现概率与淘汰
宿主鸟有一定的几率发现被寄生的蛋并将其淘汰。在算法中,这一现象通过引入一个蛋的发现概率来模拟,从而使得部分解被淘汰,增加解的多样性。
(d) Lévy飞行的搜索策略
为了模拟布谷鸟在寻找寄生巢穴时的长距离飞行行为,算法采用了Lévy飞行的搜索策略。Lévy飞行是一种随机步长的搜索过程,它使得
算法能够有效地探索搜索空间中的不同区域,从而增加找到全局最优解的概率。Lévy飞行特别适合于解决那些解空间大、解的分布不均匀的优化问题。
(e) 更新和选择
在每一轮迭代中,所有布谷鸟的解(即蛋)都会根据其适应度(即目标函数的值)被评估。根据适应度,选择一部分表现最好的布谷鸟(解)进入下一代,而表现不佳的则被淘汰。这个过程模拟了自然选择的过程,确保了算法能够逐渐逼近问题的最优解。
3. 算法特性
布谷鸟优化算法具有以下几个显著的特性:
- 强大的全局搜索能力:通过Lévy飞行的长距离探索,COA能够有效地避免陷入局部最优解,增加找到全局最优解的机会。
- 高效性和简洁性:COA算法规则简单,参数较少,容易实现,且运算效率高,适合解决多种复杂的优化问题。
- 良好的适应性和灵活性:算法可以灵活调整,适用于连续或离散、线性或非线性、单目标或多目标等各种类型的优化问题。
- 稳健性:算法对初值的选择不敏感,具有很好的稳健性,能够在不同的问题和环境中表现出稳定的搜索性能。
4. 应用领域
布谷鸟优化算法由于其独特的优点,在众多领域中得到了应用。这些应用领域包括但不限于:
- 工程优化:在工程设计和制造过程中,利用COA解决结构设计、参数优化等问题。
- 经济学和金融学:在投资组合优化、风险管理等方面的应用。
- 能源管理:用于电力系统的优化调度、能源分配和管理问题。
- 图像处理和计算机视觉:在图像分割、特征提取等领域的应用。
- 机器学习和数据挖掘:用于特征选择、聚类分析、分类器优化等。
5. 结论
布谷鸟优化算法是一种高效、灵活且应用广泛的优化工具。它通过模拟布谷鸟的独特行为,为解决复杂的优化问题提供了新的思路和方法。随着研究的深入和技术的发展,布谷鸟优化算法在更多领域的应用将会持续扩大,其性能和效率也将进一步提高。
2、仿真结果演示

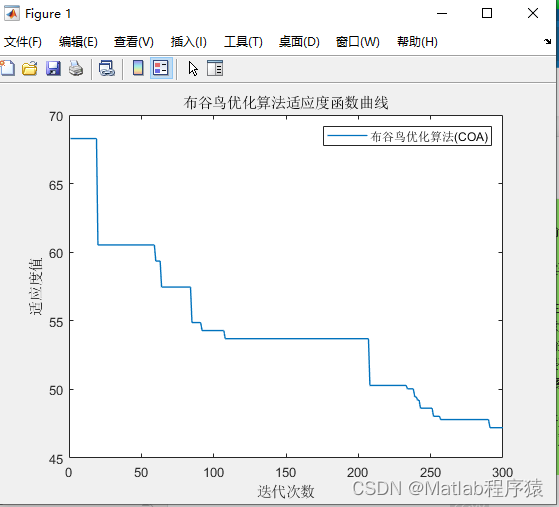
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
相关文章:

【MATLAB源码-第168期】基于matlab的布谷鸟优化算法(COA)机器人栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 布谷鸟优化算法(Cuckoo Optimization Algorithm, COA)是一种启发式搜索算法,其设计灵感源自于布谷鸟的独特生活习性,尤其是它们的寄生繁殖行为。该算法通过模拟布谷鸟在自然界中…...
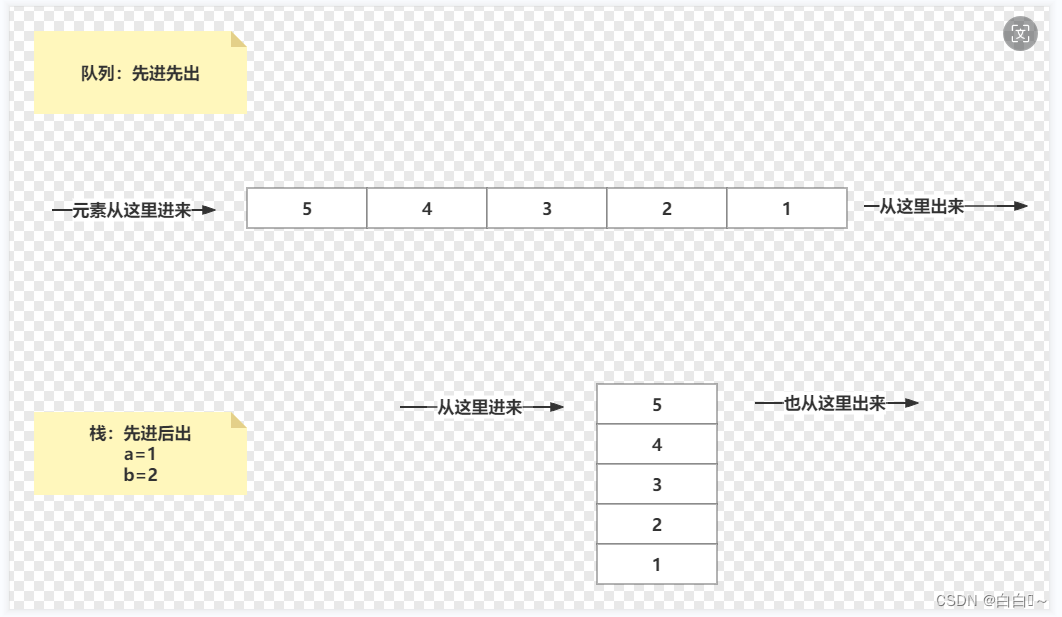
集合深入------理解底层。
集合的使用 前提:栈、堆、二叉树、hashcode、toString()、quesalus()的知识深入和底层理解。 1、什么是集合 集合就是咋们所说的容器 前面我们学习过数组 数组也是容器 容器:装东西的 生活中有多少的容器呀? 水杯 教室 酒瓶 水库 只要是…...

【阅读笔记】《硬笔书法艺术》
硬笔书法基础教程,也介绍了一些实用案例 作者: 万应均 出版社: 湖南人民出版社 笔记 CH1 运笔方式 起笔:起笔、切笔、顺峰、搭峰。 行笔:提笔、按笔、滑笔、转笔、折笔。 收笔:提收、顿收、折收。 CH2 钢笔楷书 “古人善书者…...

5.5.5、【AI技术新纪元:Spring AI解码】使用PGvector设置向量存储及进行相似性搜索
使用PGvector设置向量存储及进行相似性搜索 本节指导您如何设置PGvector VectorStore来存储文档嵌入并执行相似性搜索。 PGvector是一个开源的PostgreSQL扩展,能够支持存储和搜索机器学习生成的嵌入向量,提供查找精确和近似最近邻的功能。它设计得与PostgreSQL的其他特性无…...

EDR下的线程安全
文章目录 前记进程断链回调执行纤程内存属性修改early birdMapping后记reference 前记 触发EDR远程线程扫描关键api:createprocess、createremotethread、void(指针)、createthread 为了更加的opsec,尽量采取别的方式执行恶意代…...

洛谷刷题 | B3623 枚举排列
枚举排列 题目描述 今有 n n n 名学生,要从中选出 k k k 人排成一列拍照。 请按字典序输出所有可能的排列方式。 输入格式 仅一行,两个正整数 n , k n, k n,k。 输出格式 若干行,每行 k k k 个正整数,表示一种可能的队…...

程序员35岁会失业吗?
程序员35岁会失业吗? 35岁被认为是程序员职业生涯的分水岭,许多程序员开始担忧自己的职业发展是否会受到年龄的限制。有人担心随着年龄的增长,技术更新换代的速度会使得资深程序员难以跟上;而另一些人则认为,丰富的经…...
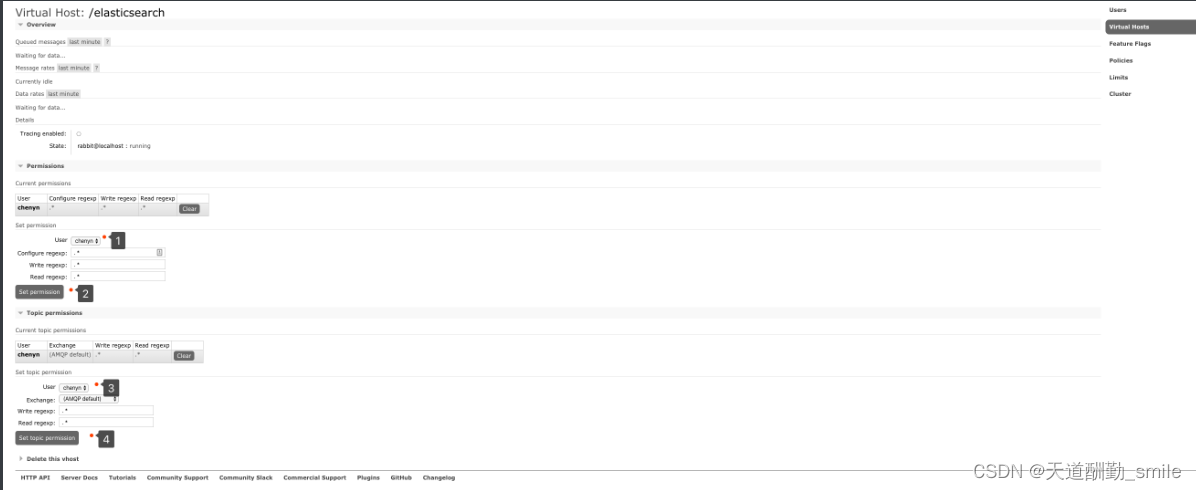
RabbitMQ 安装保姆级教程
目录 1.MQ引言 1.1 什么是MQ 1.2 MQ有哪些 1.3 不同MQ特点 2.RabbitMQ 的引言 2.1 RabbitMQ 2.2 RabbitMQ 的安装 2.2.1 下载 2.2.2 下载的安装包 2.2.3 安装步骤 3. RabiitMQ 配置 3.1RabbitMQ 管理命令行 3.2 web管理界面介绍 3.2.1 overview概览 3.2.2 Admin用…...
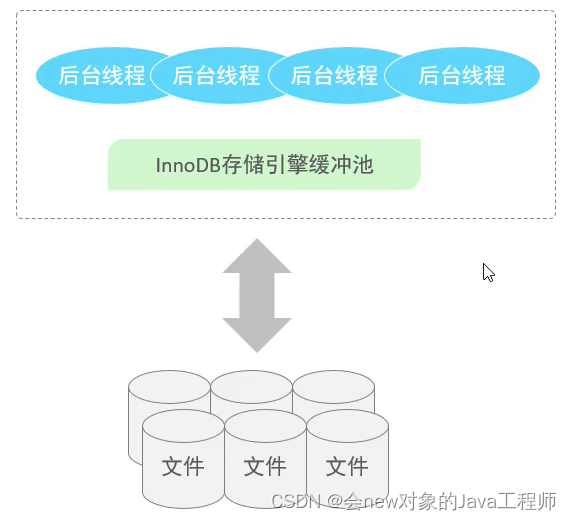
【MySQL】InnoDB引擎
逻辑结构 InnoDB存储引擎逻辑结构如图所示: Tablespace:表空间,一个数据库可以对应多个表空间。数据库中的每张表都有一个表空间,用来存放表记录、索引等数据。 Segment:段,表空间中有多个段,…...
小白如何兼职赚得第一桶金?六大网络赚钱方式助你轻松开启副业之旅
小白如何兼职赚得第一桶金?六大网络赚钱方式助你轻松开启副业之旅 无需担忧,以下为你精心挑选的六大线上兼职方式,将助你轻松开启副业赚钱之旅。 1,参与网络调查:市场调研公司及品牌商为洞察消费者需求,常…...

富格林:出金不顺谨防虚假受害
富格林悉知,做投资有盈有亏是正常的,投资者需要做的是尽可能降低亏损的风险,警惕虚假出金陷阱,避免造成不必要的亏损。在进入黄金投资市场之前,投资者需学习一定的投资技巧,并且需要采取正规的策略来打击和…...

Saltstack 最大打开文件数问题之奇怪的 8192
哈喽大家好,我是咸鱼。 今天分享一个在压测过程中遇到的问题,当时排查这个问题费了我们好大的劲,所以我觉得有必要写一篇文章来记录一下。 问题出现 周末在进行压测的时候,测试和开发的同事反映压测有问题,请求打到…...
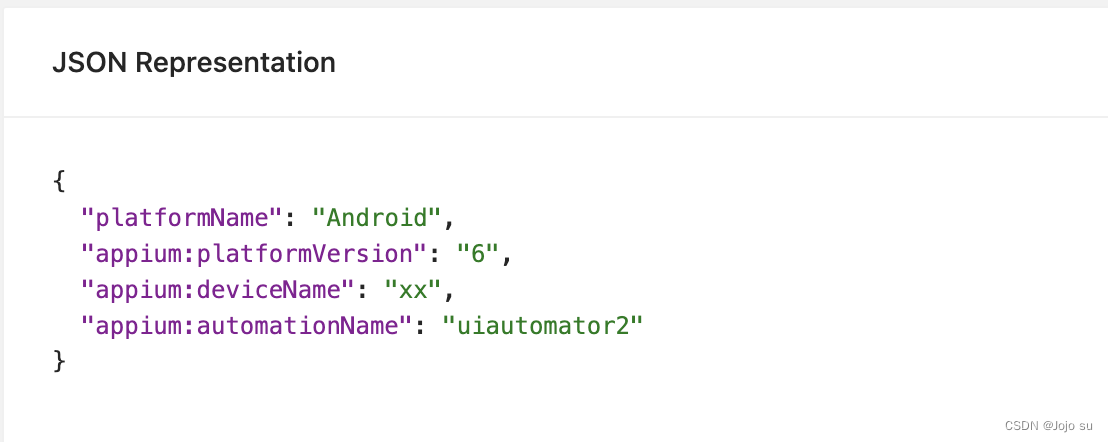
Appium Inspector 展示设备当前页面
定位元素需要使用appium inspector,之前每次都是从登录页开始,后来发现连接设备的时候只需要去掉appPackage、appActivity即可。 { "platformName": "Android", "platformVersion": "6", "deviceNa…...
PyQt:实现菜单栏的点击拖动效果
一、整体步骤 1.设计UI文件 2.调用显示 3.效果展示 二、设计UI文件 1.添加 Scroll Area控件,作为菜单栏的布置区域 2.设置 Scroll Area控件的属性 3.Scroll Area控件内放置 按钮控件 组成菜单栏 此处,放置了需要了6个按钮,并设置按钮的固…...

力扣--并查集547.省份数量
思路分析: 首先定义变量 fa 用于记录并查集,以及城市数量 n。定义了并查集的两个函数,find 用于查找节点的根节点,togother 用于合并两个节点所在的集合。在公共函数 findCircleNum 中,初始化并查集,然后遍…...

leetcode35-Search Insert Position
排序数组搜索某个元素,这种思维一定要往二分法上靠 public class searchInsertPosition{public static void main(String[] args) {int arr[] {1,3,5,6};System.out.println(getIndex(arr,2));}public static int getIndex(int[] arr,int target) {int start 0;i…...

API 接口渗透测试
1 API 接口介绍 1.1 RPC(远程过程调用) 远程过程调用(英语:Remote Procedure Call,缩写为 RPC)是一个计算机通信协议。该协议允许运行于一台计算机的程序调用另一台计算机的子程序,而程序员无…...

oracle 19c单机版本补丁升级
文章目录 一、补丁包概述二、备份opatch三、替换高版本opatch四、打DB补丁1、关闭数据库2、关闭监听3、解压补丁4、冲突检测5、补丁空间检查6、执行补丁升级7、将更新内容加载到数据库8、最后查看数据库版本9、卸载补丁包 一、补丁包概述 补丁升级包 链接:https://…...

推荐系统的未来:大模型驱动的个性化推荐技术与挑战
推荐系统的未来:大模型驱动的个性化推荐技术与挑战 1. 背景介绍 推荐系统是现代互联网服务中不可或缺的一部分,它通过分析用户的历史行为和偏好,为用户提供个性化的内容推荐,从而提高用户体验和满意度。随着大数据、机器学习和人…...

Allegro许可管理工具
在数字化时代,软件许可管理成为企业面临的挑战之一。如何确保软件的合规使用、优化资源配置并降低运营成本是企业关注的焦点。Allegro许可管理工具作为一款强大的管理工具,为企业提供了全面、高效的解决方案。本文将深入探讨Allegro许可管理工具的卓越实…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
