数据挖掘终篇!一文学习模型融合!从加权融合到stacking, boosting
模型融合:通过融合多个不同的模型,可能提升机器学习的性能。这一方法在各种机器学习比赛中广泛应用, 也是在比赛的攻坚时刻冲刺Top的关键。而融合模型往往又可以从模型结果,模型自身,样本集等不同的角度进行融合。
数据及背景
零基础入门数据挖掘 - 二手车交易价格预测_学习赛_赛题与数据_天池大赛-阿里云天池的赛题与数据(阿里天池-零基础入门数据挖掘)
模型融合
如果你打算买一辆车,你会直接走进第一家4S店,然后在店员的推销下直接把车买了吗?大概率不会,你会先去网站,看看其他人的评价或者一些专业机构在各个维度上对各种车型的对比;也许还会取咨询朋友和同事的意见。最后,做出决策。
模型融合采用的是同样的思想,即多个模型的组合可以改善整体的表现。集成模型是一种能在各种的机器学习任务上提高准确率的强有力技术。
模型融合是比赛后期一个重要的环节,大体来说有如下的类型方式:
1. 简单加权融合:
-
回归(分类概率):算术平均融合(Arithmetic mean),几何平均融合(Geometric mean);
-
分类:投票(Voting);
-
综合:排序融合(Rank averaging),log融合。
2. stacking/blending:
-
构建多层模型,并利用预测结果再拟合预测。
3. boosting/bagging:
-
多树的提升方法,在xgboost,Adaboost,GBDT中已经用到。
平均法(Averaging)
基本思想:对于回归问题,一个简单直接的思路是取平均。稍稍改进的方法是进行加权平均。权值可以用排序的方法确定,举个例子,比如A、B、C三种基本模型,模型效果进行排名,假设排名分别是1,2,3,那么给这三个模型赋予的权值分别是3/6、2/6、1/6。
平均法或加权平均法看似简单,其实后面的高级算法也可以说是基于此而产生的,Bagging或者Boosting都是一种把许多弱分类器这样融合成强分类器的思想。
简单算术平均法:如果公式查看不了,请点击【文章原文】
Averaging方法就多个模型预测的结果进行平均。这种方法既可以用于回归问题,也可以用于对分类问题的概率进行平均。
加权算术平均法:
这种方法是平均法的扩展。考虑不同模型的能力不同,对最终结果的贡献也有差异,需要用权重来表征不同模型的重要性importance。
投票法(voting)
基本思想:假设对于一个二分类问题,有3个基础模型,现在我们可以在这些基学习器的基础上得到一个投票的分类器,把票数最多的类作为我们要预测的类别。
绝对多数投票法:最终结果必须在投票中占一半以上。
相对多数投票法:最终结果在投票中票数最多。
加权投票法:其原理为
硬投票:对多个模型直接进行投票,不区分模型结果的相对重要度,最终投票数最多的类为最终被预测的类。
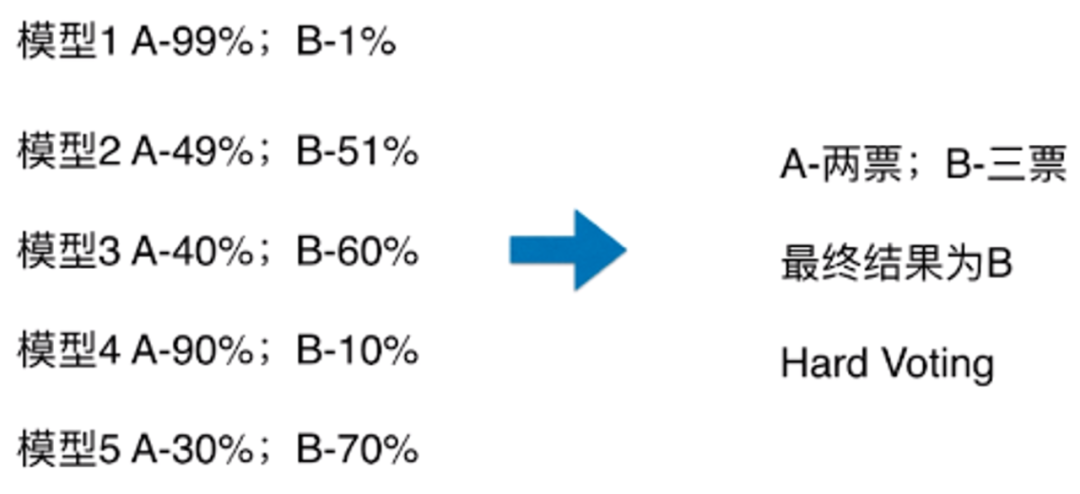
软投票:增加了设置权重的功能,可以为不同模型设置不同权重,进而区别模型不同的重要度。

from sklearn.tree import DecisionTreeClassifierfrom sklearn.neighbors import KNeighborsClassifierfrom sklearn.linear_model import LogisticRegressionfrom sklearn.ensemble import VotingClassifier
model1 = LogisticRegression(random_state=2020)model2 = DecisionTreeClassifier(random_state=2020)model = VotingClassifier(estimators=[('lr', model1), ('dt', model2)], voting='hard')model.fit(x_train, y_train)model.score(x_test, ytest)
<section role="presentation" data-formula="H(\boldsymbol x)=c{arg \max\limitsj\sum{i=1}^Tw_ih_i^j(\boldsymbol x)}
" data-formula-type="block-equation" style="text-align: left;overflow: auto;">
查看本文全部内容,欢迎访问天池技术圈官方地址:数据挖掘终篇!一文学习模型融合!从加权融合到stacking, boosting
相关文章:

数据挖掘终篇!一文学习模型融合!从加权融合到stacking, boosting
模型融合:通过融合多个不同的模型,可能提升机器学习的性能。这一方法在各种机器学习比赛中广泛应用, 也是在比赛的攻坚时刻冲刺Top的关键。而融合模型往往又可以从模型结果,模型自身,样本集等不同的角度进行融合。 数据…...
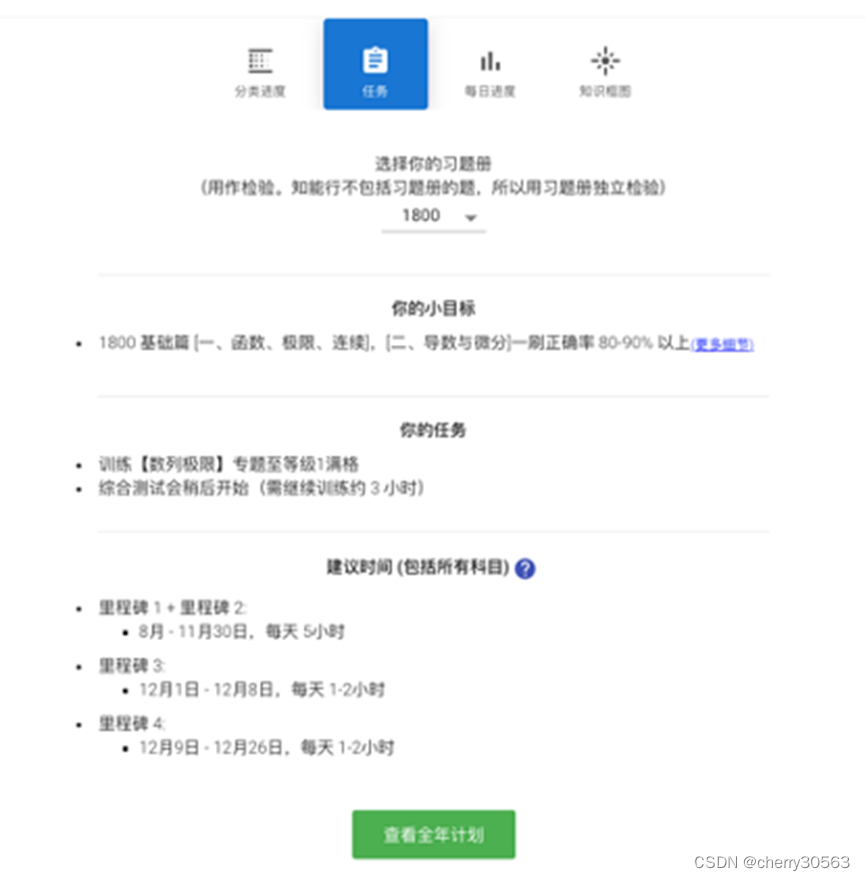
24考研数学炸了,给25考研人的启示
复习原则和要素 在选择老师、思路的时候,一定要看清楚,认不认可这个老师的复习思路。 有的老师认为大家基础不错,讲的内容可能不会特别细致。有的老师注重基础,讲的很细致,防止0基础的学生吃力。所以,思路…...
)
嵌入式学习第三十天!(单向链表练习)
1. 单向链表的逆序: int Is_Empty_Link(LINK_LIST *plist) {return plist->phead NULL; }void Reverse_Link(LINK_LIST *plist) {LINK_NODE *ptmp plist->phead;LINK_NODE *pinsert NULL;plist->phead NULL;if(Is_Empty_Link(plist)){return;}else{wh…...
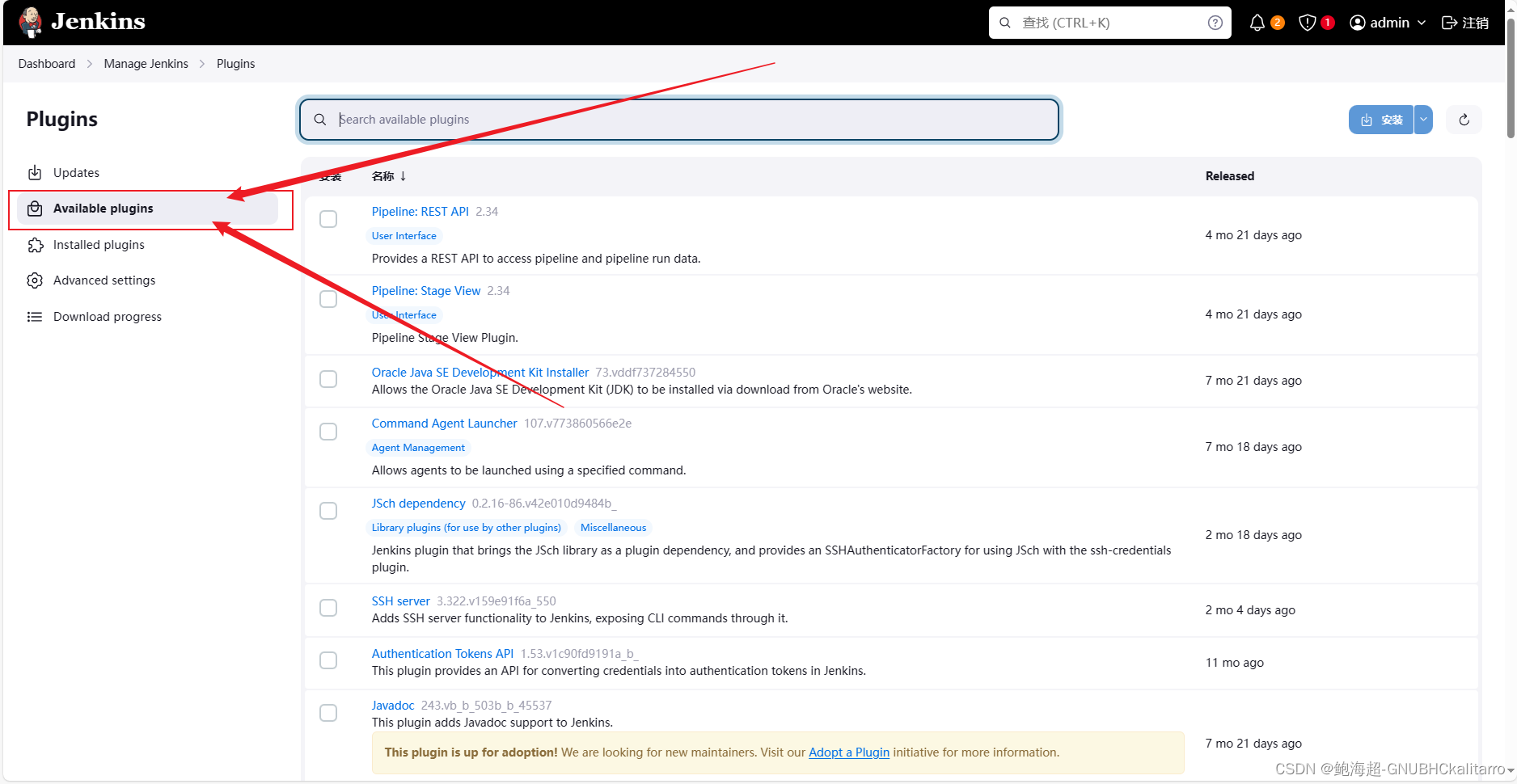
Linux:rpm部署Jenkins(1)
1.获取Jenkins安装包 我这里使用的是centos7系统,ip为:192.168.6.6 2G运存 连接外网 Jenkins需要java环境,java的jdk包你可以去网上下载离线包,或者直接去yum安装,我这里使用的是yum安装 再去获取Jenkins的rpm包…...
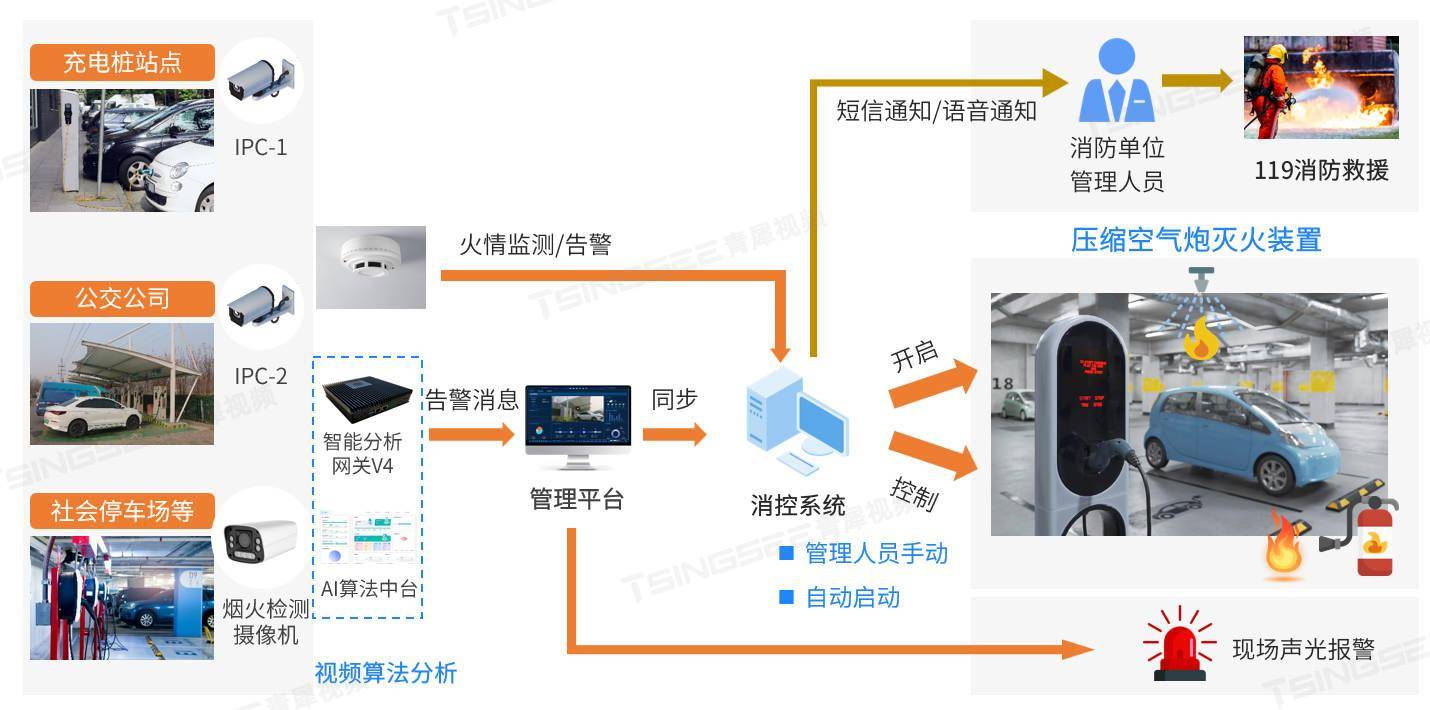
新能源汽车充电桩站点烟火AI识别检测算法应用方案
新能源汽车作为现代科技与环保理念的完美结合,其普及和应用本应带给人们更加便捷和绿色的出行体验。然而,近年来新能源汽车充电火灾事故的频发,无疑给这一领域投下了巨大的阴影。这不禁让人深思,为何这一先进的交通工具在充电过程…...

Macbook安装Go以及镜像设置
Macbook安装Go 文章概要:本文主要介绍了在MacOS上安装Go的步骤 本文内容来自:谷流仓AI - ai.guliucang.com 有两种方式安装go: 通过homebrew安装通过Go官网直接下载安装文件安装 1. 通过homebrew安装 brew update && brew install…...

群晖NAS安装Video Station结合内网穿透实现公网访问本地影音文件
文章目录 1.使用环境要求:2.下载群晖videostation:3.公网访问本地群晖videostation中的电影:4.公网条件下使用电脑浏览器访问本地群晖video station5.公网条件下使用移动端(搭载安卓,ios,ipados等系统的设备…...
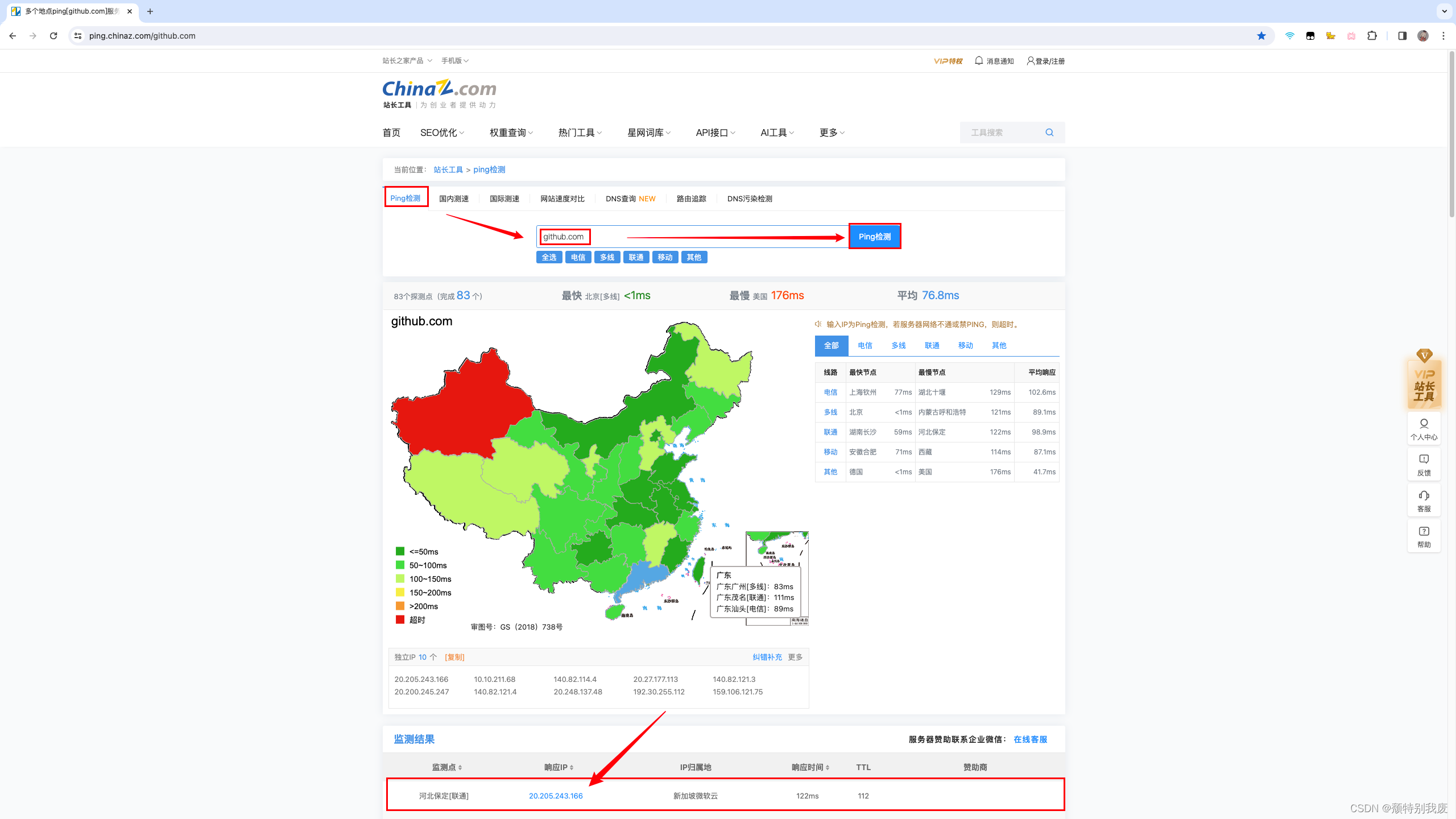
GitHub加速访问最简单的方法
Github是全球最大的代码开源平台,对于编程的小伙伴来说,这是一个巨大的宝库,也是编程学习的圣地。很对小伙伴在使用GitHub时会经常出现无法访问Github的情况。 一、解决方法——>修改hosts文件 通过 IP查询工具来获取当前Github网站的真实…...

MySQL数据库索引介绍
前言 在数据库中创建索引可以提高数据检索的速度和效率。索引是一种数据结构,类似于书籍的目录,它可以帮助数据库系统快速定位和访问表中的特定数据行。 目录 一、索引相关介绍 1. 概述 2. 作用 3. 副作用 4. 创建原则依据 二、索引的分类与管理…...

中间件学习--InfluxDB部署(docker)及springboot代码集成实例
一、需要了解的概念 1、时序数据 时序数据是以时间为维度的一组数据。如温度随着时间变化趋势图,CPU随着时间的使用占比图等等。通常使用曲线图、柱状图等形式去展现时序数据,也就是我们常常听到的“数据可视化”。 2、时序数据库 非关系型数据库&#…...
Go第三方框架--gin框架(一)
序言 Gin框架作为go语言使用最多的web框架,以其快速的响应速度和对复杂http路由配置的支持受到程序员和媛们的喜爱,几乎统治了web市场。但作为一名合格的程序员,要知其然更要知其所以然,不然八股文背的也没有啥意思。本着这个原则…...

网络安全——笔记
XSS:跨站脚本(Cross-site scripting) XSS 全称“跨站脚本”,是注入攻击的一种。其特点是不对服务器端造成任何伤害,而是通过一些正常的站内交互途径,例如发布评论,提交含有 JavaScript 的内容文…...

Maven pom.xml配置详解
pom.xml是什么? pom.xml(项目对象模型-Project Object Model的缩写)是Maven项目的核心配置文件,用于管理项目的依赖、插件、构建配置等。 举例说明:以阿里巴巴的fastjson为例: <?xml version"1.…...

2024深圳国际电线电缆及电源产品展览会
2024深圳国际电线电缆及电源产品展览会 2024 Shenzhen International Coupling, Clutch and Brake Exhibition 时间:2024年08月28-30日 地点:深圳国际会展中心(新馆) 预订以上展会详询陆先生 I38(前三位ÿ…...
如何成功将自己开发的APP上架到应用商店
随着移动应用市场的蓬勃发展,开发一款优秀的APP已成为许多企业和个人的首要选择。然而,成功上架并有效推广APP至关重要。本文将逐步介绍完整的上架流程,包括准备所需材料、注册开发者账户、进行APP备案、提交审核以及上架成功后的推广和维护。…...
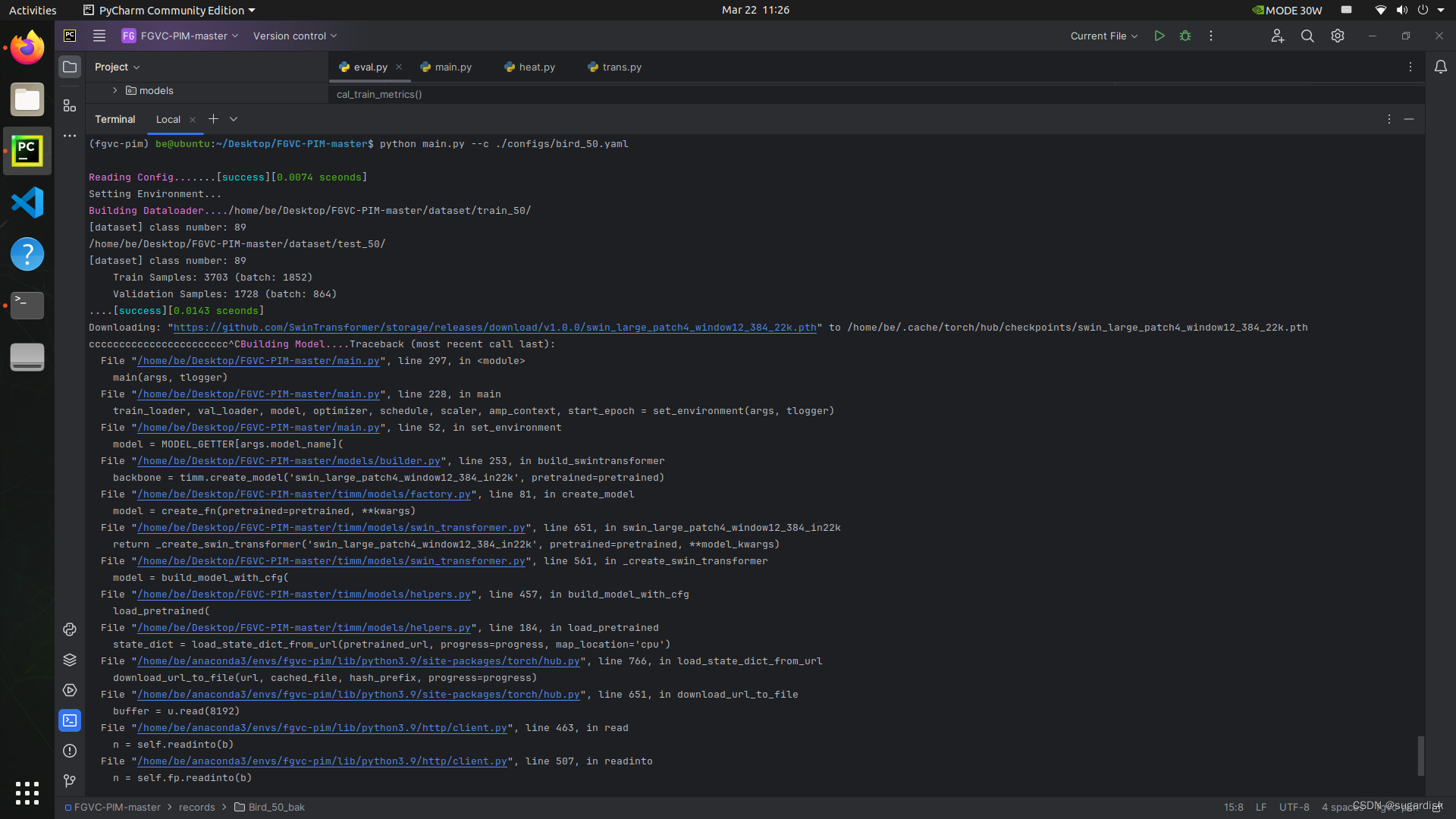
Jetson AGX ORIN 配置 FGVC-PIM 神经网络(包含 arm64 下面 torch 和 torchvision 配置内容)
Jetson AGX ORIN 配置 FGVC-PIM 神经网络 文章目录 Jetson AGX ORIN 配置 FGVC-PIM 神经网络配置 ORIN 环境创建 FGVC-PIM 虚拟环境安装 PyTorch安装 torchvision安装其他依赖包 配置 ORIN 环境 首先先配置 ORIN 的环境,可以参考这个链接: Jetson AGX …...

mybatisplus和mybatis兼容问题
Invalid bound statement (not found) 错误 原xml配置 <bean id"sqlSessionFactory" class"org.mybatis.spring.SqlSessionFactoryBean"><property name"mapperLocations" value"classpath:/META-INF/mapper/*.xml"/>&l…...
nodejs安装使用React
1、react安装 首先,确保电脑上具备nodejs环境,之后用 winr 呼出控制台,输入 cmd 命令弹出cmd控制台(小黑框)之后在默认路径输入如下代码 npm i -g create-react-app //全局安装react环境无需选择特定文件夹安装成功后…...

防御性编程,可能是导致被裁员的更大的原因,别被误导了
裁员与反裁员是当前IT界一个经典的话题,作为打工者的猿人常常讨论了N多的防御性编程,代码不可读、代码不好改、代码深度嵌套、代码留bug等等。 其实防御性编程只会让决策者加速解耦你与业务系统: 1、增加代码走查的环节(增加成本…...
)
Unity与鼠标相关的事件(自己记忆用)
1. OnMouseDown:当用户按下鼠标按钮时调用。 - 参数:MouseEvent,可以用来确定哪个鼠标按钮被按下。 2. OnMouseUp:当用户释放鼠标按钮时调用。 - 参数:MouseEvent,可以用来确定哪个鼠标按钮被释放。…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
