冒泡排序 快速排序 归并排序 其他排序

书接上回..

目录

2.3 交换排序

2.3.1冒泡排序

2.3.2 快速排序

快速排序的优化:

快速排序非递归

2.4 归并排序

基本思想

归并排序非递归

海量数据的排序问题

 排序算法时间空间复杂度和稳定性总结

四. 其他非基于比较排序 (了解)

---

2.3 交换排序

基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特

点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

2.3.1冒泡排序

遍历数组, 将最大值移动到最后, 再次遍历, 将第二大值移动到倒数第二个位置, 以此类推

思路:

1. 一共需要遍历arr.length-1趟, 才能将所有的元素变有序
2. 第1趟在遍历时, 需要交换arr.length-1次, 第2趟在编历时, 需要交换arr.length-1-1次...
3. 我们可以优化一下代码, 即只需要交换arr.length-1-i次即可, i从0开始
4. 进一步优化, 如果一趟遍历下来, .没有任何的交换进行, 则说明数组已经有序, 则不需再遍历, 直接return即可

代码:

 public static void bubbleSort(int[] arr){for (int i = 0; i < arr.length-1; i++) {int flag = 0;for (int j = 0; j < arr.length-1-i; j++) {if(arr[j]>arr[j+1]){swap(arr,j,j+1);flag = 1;}}if(flag == 0){return;}}}

【冒泡排序的特性总结】

• 冒泡排序是一种非常容易理解的排序
• 时间复杂度：O(N^2)
• 空间复杂度：O(1)
• 稳定性：稳定

2.3.2 快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

思路:

1. 对[left,right]区间进行排序
2. partition()方法的作用: 找到一个基准值pivot, 并将小于基准值的数都放在其左边, 大于基准值的数都放在其右边, 即将划分成以pivot边界的[left,pivot-1],[pivot+1,right]两部分
3. 递归基准值的左边, 即[left,pivot-1]再次进行partition, 直到left>= right
4. 递归基准值的右边, 即[pivot+1,right]再次进行partition, 直到left>= right
5. 全部完成后数组就会变有序

代码:(非最终)

 public static void quickSort(int[] arr){quick(arr,0,arr.length-1);}private static void quick(int[] arr,int left,int right){if(left >= right){return ;}int pivot = partition(arr,left,right);quick(arr,left,pivot-1);quick(arr,pivot+1,right);}

将区间按照基准值划分为左右两半部分的常见方式有： 

1.  Hoare法

假设数组的第一个数就是基准值, 运用交换的思想

思路:

1. 将left赋给pivot, 创建变量i = left; j = right,用来遍历数组
2. i从前面遍历, 找到比arr[pivot]大的数, 停下来, j从后面遍历,找到比arr[pivot]小的数, 停下来, 交换这两个下标的值, 这样就把比arr[pivot]小的数放前面, 比arr[pivot]大的数放后面
3. 继续遍历, 直到i>=j, 停止
4. 此时交换i和pivot的值,返回i下标, 即基准值的下标

代码:

private static int partition(int[] arr,int left,int right){int i = left;int j = right;int pivot = left;while(i < j){while(i < j && arr[j] >= arr[pivot]){j--;}while(i < j && arr[i] <= arr[pivot]){i++;}swap(arr,i,j);}swap(arr,i,pivot);return i;}

思考:

1. 上述里层while循环, 判断条件一定是>=  <= 吗?不取等行不行?

答案: 不行, 因为如果不加等号, 左右两边都是相同的数字时, 进不去里层循环, 外层循环死循环

2. 以左边作为基准时, 为什么一定要从右边先开始找, 而不是左边?

答案: 如果从左边开始找, 那么左右相遇的地方可能是比基准值大的数字, 那么进行交换后, 就不满足基准值左边的数都小于右边, 反之, 如果从右边开始找, 那么左右相遇的地方一定是比基准值小的数字, 这时与左边的基准值进行交换, 小的数换到左边, 满足基准值左边的数都小于右边

2. 挖坑法

假设数组的第一个数就是基准值, 运用覆盖的思想

思路:

1. 将数组第一个下标的值存起来给pivot,挖坑pivot的位置, 创建变量i = left; j = right,用来遍历数组
2. i从前面遍历, 找到比arr[pivot]大的数, 停下来, 将arr[j]放在arr[i]的位置, 此时i = 0, 在arr[j]的位置挖坑,j从后面遍历,找到比arr[pivot]小的数, 停下来,将arr[i]放在arr[j]的位置,在arr[i]的位置挖坑
3. 继续遍历, 直到i >= j, 停止
4. 最后放pivot的值放在arr[i]这个坑中即可, 返回基准值所在的下标i

代码:

 private static int partition(int[] arr,int left,int right){int i = left;int j = right;int pivot = arr[left];while(i < j){while(i<j && arr[j] >= pivot){j--;}arr[i] = arr[j];while(i<j && arr[i] <= pivot){i++;}arr[j] = arr[i];}arr[i] = pivot;return i;}

3. 前后指针(了解)

private static int partition(int[] array, int left, int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}

快速排序的优化:

1. 三数取中法选key

拿到left = 0, right = arr.length-1, 和mid为中间下标, 可以表示为mid = left + ((right-left)>>1), 比较这三个数的大小, 将中间大小的数字作为基准值, 这样可以保证基准值的左右两边都有数据, 减小时间复杂度

private static int middleNum(int[] arr,int left,int right){int mid = left + ((right-left)>>1);if (arr[left] < arr[right]){if(arr[mid] < arr[left]){return left;}else if(arr[mid] > arr[right]){return right;}else{return mid;}}else{if(arr[mid] < arr[right]){return right;}else if(arr[mid] > arr[left]){return left;}else{return mid;}}}private static void quick(int[] arr,int left,int right){if(left >= right){return ;}//优化1int index = middleNum(arr,left,right);swap(arr,index,left);int pivot = partition(arr,left,right);quick(arr,left,pivot-1);quick(arr,pivot+1,right);}

2. 递归到小的子区间时，可以考虑使用插入排序

当区间变小时, 再使用递归的方法进行排序, 会浪费时间, 所以当区间小于一个数(假设10)时, 就采用直接插入排序, 提高效率

 private static void quick(int[] arr,int left,int right){if(left >= right){return ;}//优化1int index = middleNum(arr,left,right);swap(arr,index,left);//优化2if(right-left+1 <= 10 ){insertSort2(arr,left,right);return;}int pivot = partition(arr,left,right);quick(arr,left,pivot-1);quick(arr,pivot+1,right);}public static void insertSort2(int[] arr,int left,int right){for (int i = 1 + left; i <=right ; i++) {int tmp = arr[i];int j = i-1;for ( ; j >= 0; j--) {if(arr[j] > tmp){arr[j+1] = arr[j];}else{//arr[j+1] = tmp;break;}}arr[j+1] = tmp;}}

快速排序非递归

思路:

1. 使用partition方法找到基准值的下标
2. 判断如果基准值的左边不止有一个数据, 即pivot-1 > left, 则需要继续划分, 则将这一划分的左右坐标分别压入栈中, 注意在出栈时先右后左

代码:

public static void quickSortNorR(int[] arr){int left = 0;int right = arr.length-1;int pivot = partition(arr,left,right);Stack<Integer> stack = new Stack<>();if(pivot - 1 > left){stack.push(left);stack.push(pivot - 1);}if(pivot + 1 < right){stack.push(pivot+1);stack.push(right);}while(!stack.isEmpty()){right = stack.pop();left = stack.pop();pivot = partition(arr,left,right);if(pivot - 1 > left){stack.push(left);stack.push(pivot - 1);}if(pivot + 1 < right){stack.push(pivot+1);stack.push(right);}}}

快速排序总结

• 时间复杂度：O(N*logN)
• 空间复杂度：O(logN)
• 稳定性：不稳定
• 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2.4 归并排序

基本思想

归并排序（ MERGE-SORT ）是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法（ Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

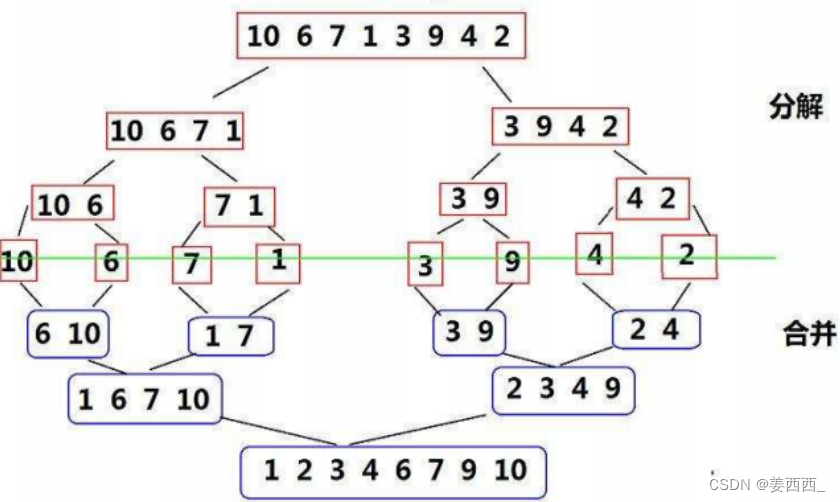
思路:

1. 归并排序分为两部分, 分解和合并, 分解我们运用到的思路是递归, 合并我运用到的思路是用新数组存储有序序列, 再赋值给原数组
2. 分解: 找到数组的中间下标mid, 左下标left, 右下标right, 将数组分解成[left, mid] 和[mid+1,right], 递归分解, 直到只剩下一个元素
3. 合并:将两组数据的头和尾分别定义成s1e1 和s2e2, s1和s2依次进行比较, 小的就存放在新数组里, 并++,直到有一个数组的s1 > s2, 结束比较, 直接将另一组数据剩下的加到新数组的后面, 最后将新数组赋值给原数组, 注意: 新数组和原数组的对应关系是:arr[i+left] = tmpArr[i]

代码:

  public static void mergeSort(int[] arr){mergeFunc(arr,0,arr.length-1);}private static void mergeFunc(int[] arr,int left,int right){if(left >= right){return ;}int mid = left+((right-left)>>1);mergeFunc(arr,left,mid);mergeFunc(arr,mid+1,right);merge(arr,left,mid,right);}private static void merge(int[] arr, int left,int mid,int right){int s1 = left;int s2 = mid +1;int e1 = mid;int e2 = right;int[] tmpArr = new int[right-left+1];int k = 0;while(s1 <= e1 && s2 <= e2){if(arr[s1] > arr[s2]){tmpArr[k++] = arr[s2++];}else{tmpArr[k++] = arr[s1++];}}while(s1 <= e1){tmpArr[k++] = arr[s1++];}while(s2 <= e2){tmpArr[k++] = arr[s2++];}for (int i = 0; i < k; i++) {arr[i+left] = tmpArr[i];}}

归并排序非递归

思路:

1. 设gap, 表示几个元素为一半, 归并是将一组分成两半进行比较的,比较的事交给merge方法, 我们只需要知道怎么分组, 并找好下一组的位置, 每次gap*=2, 当gap >arr.length时, 说明已经全部有序了
2. 用 i 来遍历数组找位置, i=0 时, 那么第一组的left就是0, mid就是left+gap-1, right就是mid+gap, 注意:为了防止mid和right越界, 当mid right>= arr.length时, 说明超过了数组的大小, 只需将他们设置成最后一个元素即可
3. i在找下一组时, i应该等于i+2*gap, 因为一组的长度为2*gap

代码:
 

public static void mergeSortNorR(int[] arr){int gap = 1;while(gap < arr.length){for (int i = 0; i < arr.length; i=i+2*gap) {int left = i;int mid = left + gap -1;if(mid >= arr.length){mid = arr.length-1;}int right = mid +gap;if(right >= arr.length){right = arr.length-1;}merge(arr,left,mid,right);}gap *= 2;}}

归并排序总结

• 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
• 时间复杂度：O(N*logN)
• 空间复杂度：O(N)
• 稳定性：稳定

海量数据的排序问题

外部排序：排序过程需要在磁盘等外部存储进行的排序

前提：内存只有 1G ，需要排序的数据有 100G

因为内存中因为无法把所有数据全部放下，所以需要外部排序，而归并排序是最常用的外部排序

1. 先把文件切分成 200 份，每个 512 M

2. 分别对 512 M 排序，因为内存已经可以放的下，所以任意排序方式都可以

3. 进行 2 路归并，同时对 200 份有序文件做归并过程，最终结果就有序了

 排序算法时间空间复杂度和稳定性总结

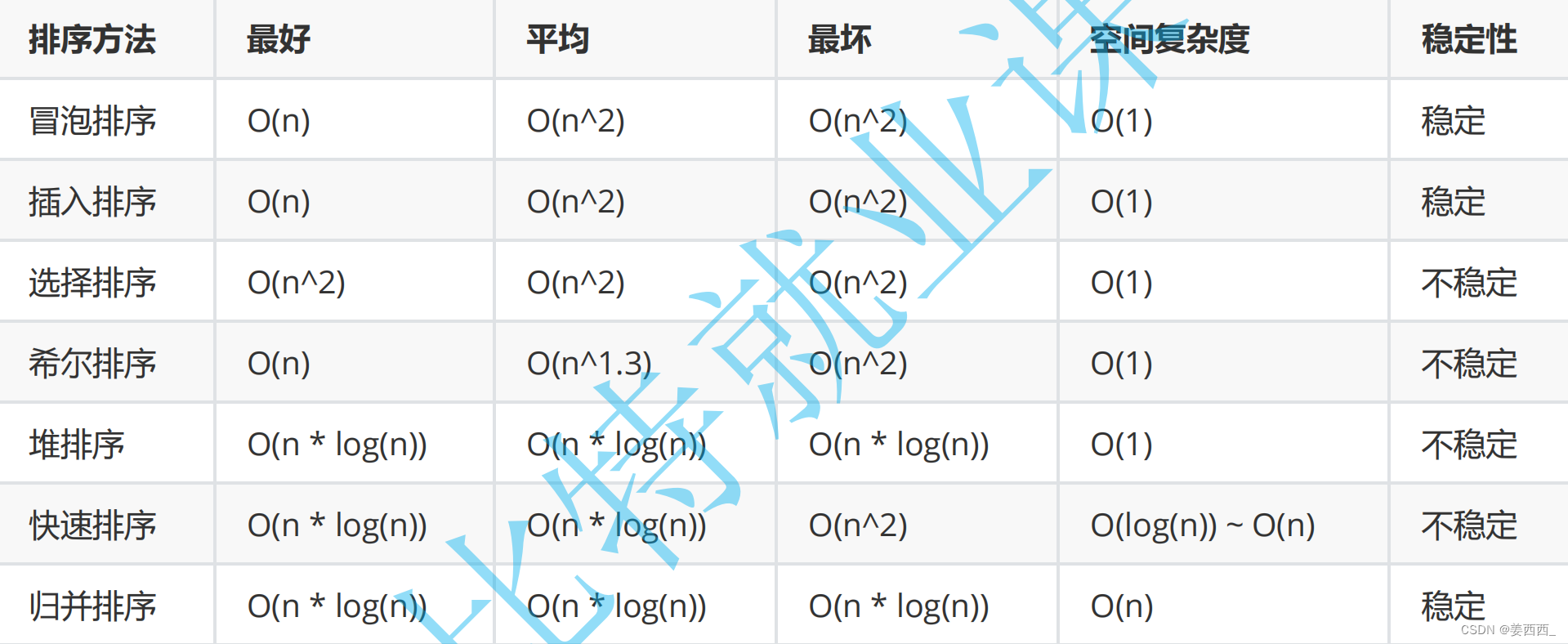
四. 其他非基于比较排序 (了解)

1. 计数排序

思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。

操作步骤：

1.  统计相同元素出现次数
2.  根据统计的结果将序列回收到原来的序列中

【 计数排序的特性总结 】

• 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
• 时间复杂度：O(MAX(N,范围))
• 空间复杂度：O(范围)
• 稳定性：稳定

2. 基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

步骤:

1. 先比较个位数字, 依次放在有顺序的10个队列中, 分别代表数字0~9, 然后从第一个队列开始出队
2. 再按照十位数字比较, 继续放入, 再出队, 循环最大数字的位数次结束

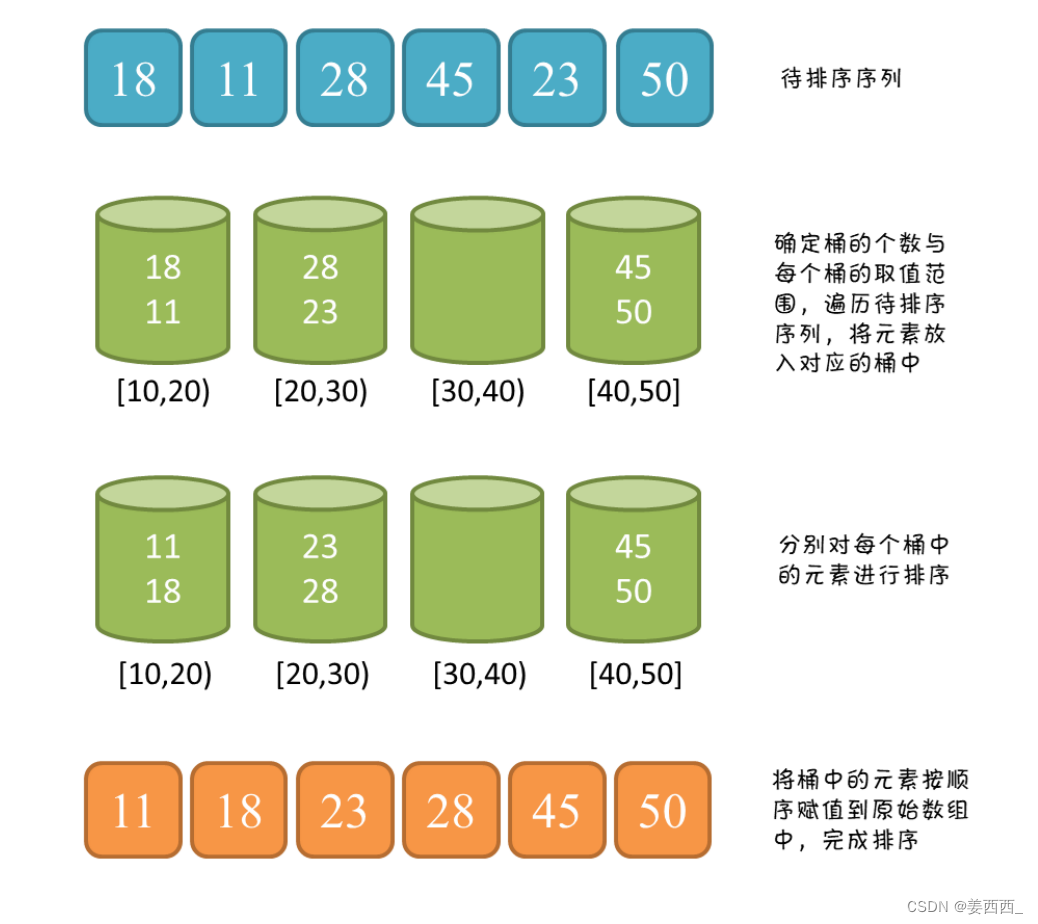
 3. 桶排序

思想:划分多个范围相同的区间，每个子区间自排序，最后合并。