【数学】 【分数】 【字符串】972. 相等的有理数
本文涉及知识点
数学 分数 字符串
LeetCode972. 相等的有理数
给定两个字符串 s 和 t ,每个字符串代表一个非负有理数,只有当它们表示相同的数字时才返回 true 。字符串中可以使用括号来表示有理数的重复部分。
有理数 最多可以用三个部分来表示:整数部分 、小数非重复部分 和小数重复部分 <(><)>。数字可以用以下三种方法之一来表示:
例: 0 ,12 和 123
<.>
例: 0.5 , 1. , 2.12 和 123.0001
<.><(><)>
例: 0.1(6) , 1.(9), 123.00(1212)
十进制展开的重复部分通常在一对圆括号内表示。例如:
1 / 6 = 0.16666666… = 0.1(6) = 0.1666(6) = 0.166(66)
示例 1:
输入:s = “0.(52)”, t = “0.5(25)”
输出:true
解释:因为 “0.(52)” 代表 0.52525252…,而 “0.5(25)” 代表 0.52525252525…,则这两个字符串表示相同的数字。
示例 2:
输入:s = “0.1666(6)”, t = “0.166(66)”
输出:true
示例 3:
输入:s = “0.9(9)”, t = “1.”
输出:true
解释:“0.9(9)” 代表 0.999999999… 永远重复,等于 1 。[有关说明,请参阅此链接]
“1.” 表示数字 1,其格式正确:(IntegerPart) = “1” 且 (NonRepeatingPart) = “” 。
提示:
每个部分仅由数字组成。
整数部分 不会以零开头。(零本身除外)
1 <= .length <= 4
0 <= .length <= 4
1 <= .length <= 4
循环小数变分数
令 x = 0.(abcd)。则 10000 × \times × x = abcd.(abcd) = abcd + x
→ \rightarrow → 10000x = abcd+x → \rightarrow → x = abcd/9999。
将小数转成分数,再比较,这样比较稳妥。 时间上用double 也可以。
代码
核心代码
class Solution {
public:bool isRationalEqual(string s, string t) {double d1 = Parse(s);double d2 = Parse(t);return abs(d1 - d2) < 0.001 * 0.001 * 000.1 * 0.1;}double Parse(string s){double dRet = 0;int iPos = s.find('.');string strInt = s.substr(0, (-1 == iPos) ? s.length() : iPos);dRet += atoi(strInt.c_str());if (-1 == iPos){return dRet;}s = s.substr(iPos + 1);iPos = s.find("(");string strNotRepeat = s.substr(0, (-1 == iPos) ? s.length() : iPos);dRet += atoi(strNotRepeat.c_str()) / pow(10.0, strNotRepeat.length());if (-1 == iPos){return dRet;}s = s.substr(iPos + 1);s.pop_back();//除掉)dRet += atoi(s.c_str()) / (pow(10.0, s.length())-1) / pow(10.0, strNotRepeat.length());return dRet;}
};
template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{string s, t;{Solution sln;s = "0.(52)", t = "0.5(25)";auto res = sln.isRationalEqual(s, t);Assert(true, res);}{Solution sln;s = "0.1666(6)", t = "0.166(66)";auto res = sln.isRationalEqual(s, t);Assert(true, res);}{Solution sln;s = "0.9(9)", t = "1.";auto res = sln.isRationalEqual(s, t);Assert(true, res);}{Solution sln;s = "8.123(4567)", t = "8.123(4566)";auto res = sln.isRationalEqual(s, t);Assert(false, res);}}
2023年7月
class Solution {
public:
bool isRationalEqual(string s, string t) {
return abs(Parse(s) - Parse(t)) < 0.00000001;
}
double Parse(const string& s)
{
int iInt = 0;
int i = 0;
for (; ( i < s.length() ) && ( s[i] != ‘.’); i++ )
{
iInt = iInt * 10 + s[i] - ‘0’;
}
i++;
double d = 0;
double dMul =1;
for (; (i < s.length()) && (s[i] != ‘(’); i++)
{
dMul *= 0.1;
d += dMul * (s[i] - ‘0’);
}
i++;
double iCycMul = 1;
int iCyc = 0;
for (; (i < s.length()) && (s[i] != ‘)’); i++)
{
iCycMul *= 0.1;
iCyc = iCyc * 10 + s[i] - ‘0’;
}
if (iCyc > 0)
{
d += iCyc * iCycMul / (1 - iCycMul) * dMul;
}
return d + iInt;
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【数学】 【分数】 【字符串】972. 相等的有理数
本文涉及知识点 数学 分数 字符串 LeetCode972. 相等的有理数 给定两个字符串 s 和 t ,每个字符串代表一个非负有理数,只有当它们表示相同的数字时才返回 true 。字符串中可以使用括号来表示有理数的重复部分。 有理数 最多可以用三个部分来表示&…...

【4】DongshanPI-Seven 应用开发_文件IO
目录 1.文件IO1.1 文件IO分类1.2 查看系统调用IO用法 2. open 函数3. write 函数4. read 函数5 dup函数 1.文件IO 1.1 文件IO分类 在Linux系统中,一切都是“文件”:普通文件、驱动程序、网络通信等。所有的操作都是通过文件IO来操作的。 在Linux操作文…...

SEO 的未来:GPT 和 AI 如何改变关键词研究
谷歌Gemini与百度文心一言:AI训练数据的较量 介绍 想象一下,有一个工具不仅可以理解错综复杂的关键字网络,还可以预测搜索引擎查询的变化趋势。 这就是生成式预训练 Transformer (GPT) 和其他人工智能技术发挥作用的地方,以我们从…...
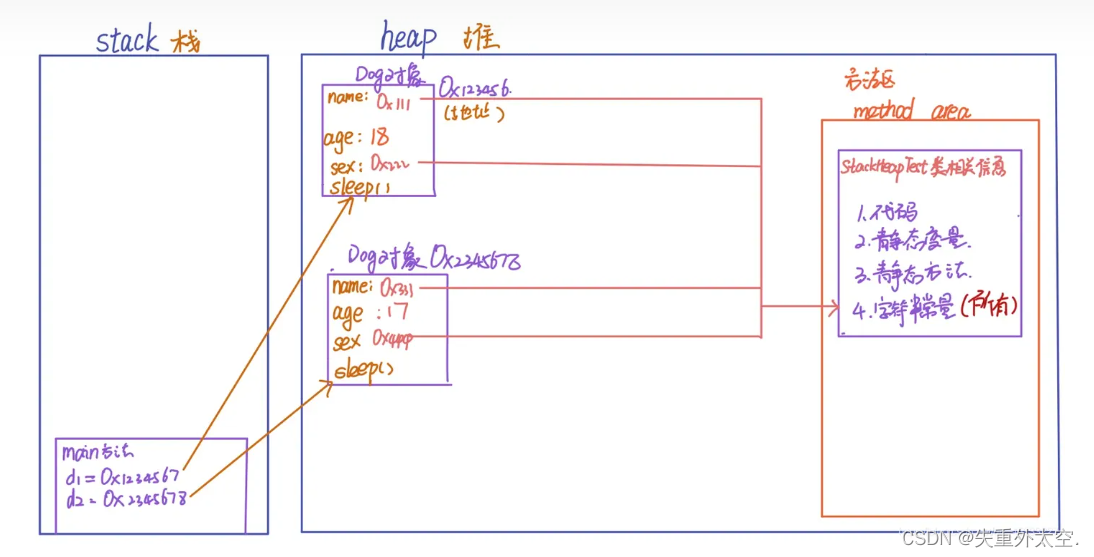
面试八股文之JAVA基础
JAVA基础 DNS、CDN?如何实现对象克隆?父子类静态代码块, 非静态代码块, 构造方法执行顺序?String s new String("abc") 创建了几个对象, 分别放到哪里?OSI网络模型七层?应用层协议?http协议和https协议区别?传输层协…...

网络连接中——长连接和短连接详解
一、TCP功能 TCP在真正开始进行数据传输之前,Server 和 Client 之间必须建立一个连接。当数据传输完成后,双方不再需要这个连接时,就可以释放这个连接。 TCP连接的建立是通过三次握手,而连接的释放是通过四次挥手。所以说,每个TCP连接的建立和释放都是需要消耗资源和时间…...
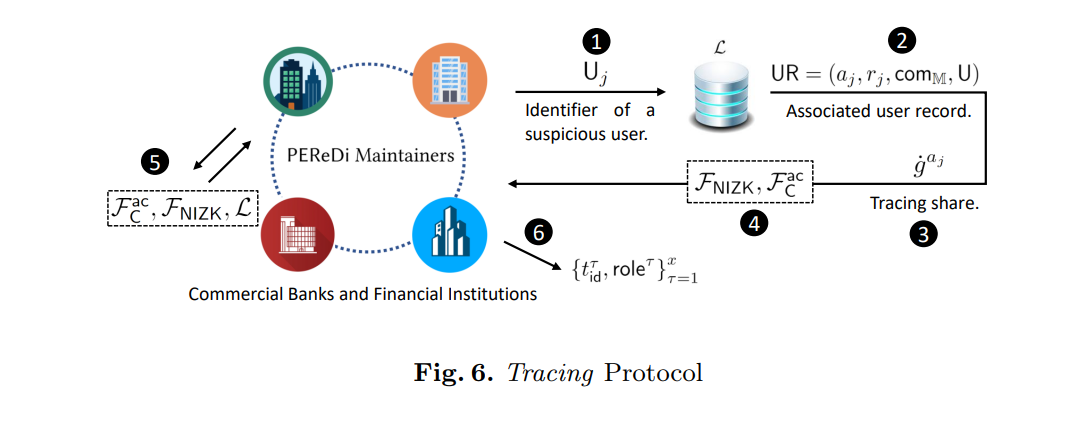
PEReDi 完全隐私的央行数字货币方案
第一个对完全隐私保护建模的方案,基于账户模型,要求交易双方都在线。 角色分类 中央银行 B B B:负责发行数字货币和货币政策,但不控制用户账户的状态,没有能力对交易的发送者或接收者进行去匿名化或披露与特定交易相…...

yolov5+pyside6+登录+用户管理目标检测可视化源码
一、软件简介 这是基于yolov5目标检测实现的源码,提供了用户登录功能界面; 用户需要输入正确的用户名和密码才可以登录。如果是超级管理员,可以修改普通用户的信息,并且在检测界面的右上角显示【管理用户】按钮。 支持图片、视频、…...

电脑如何设置个性便签 电脑个性便签分享
每次坐在电脑前,我都仿佛置身于一片信息的海洋。工作、生活、学习,方方面面的事情都需要我用心去记录。在这样一个快节奏的时代,电脑无疑成了我最得力的助手。但记事的时候,我总希望有一个既方便又有个性的工具,能让我…...
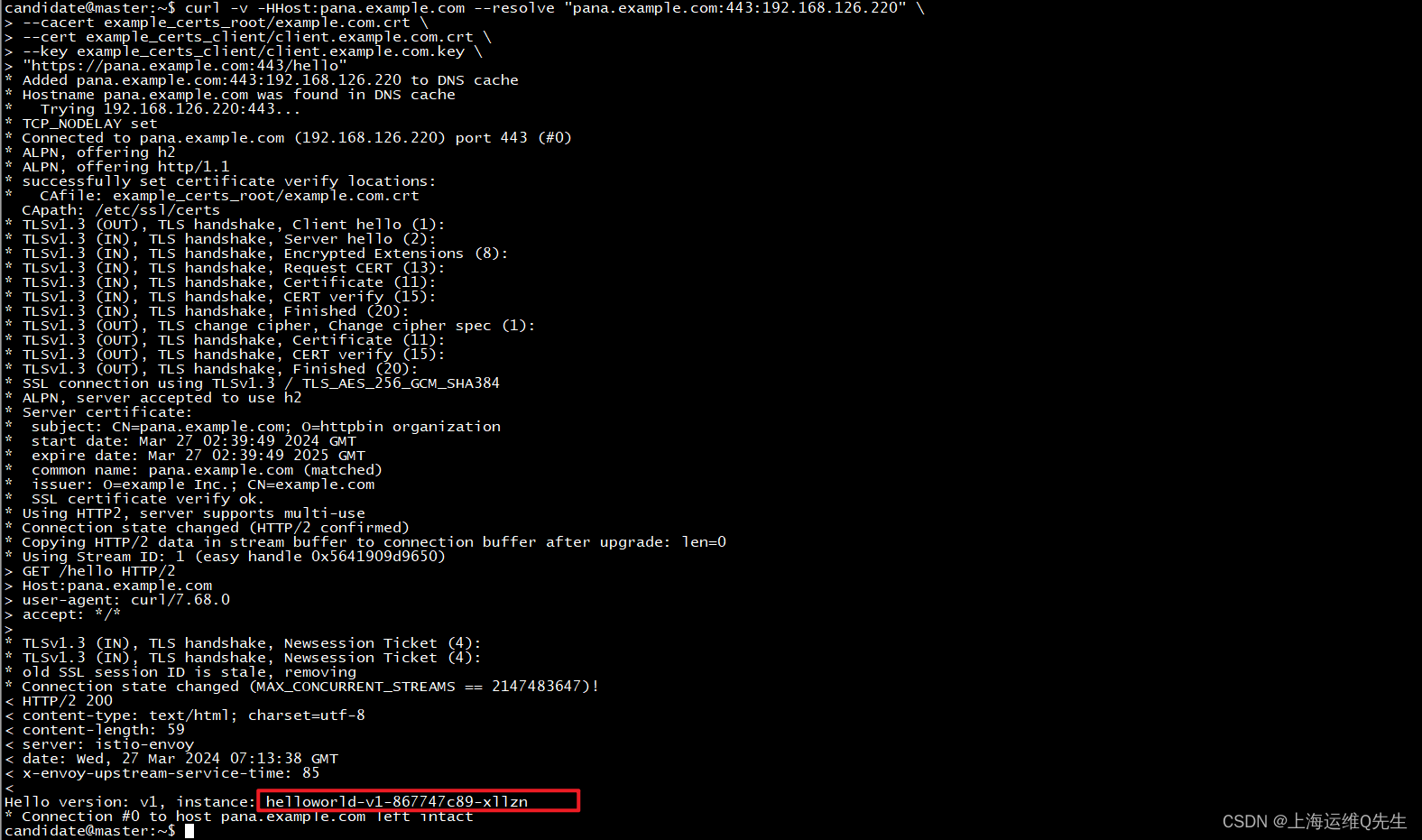
备考ICA----Istio实验12---配置双向TLS Istio Ingress Gateway实验
备考ICA----Istio实验12—配置双向TLS Istio Ingress Gateway实验 本实验部分配置延续上个Istio实验11 1. 重新配置secret 重新配置secret使其带有ca证书可以验证客户端证书是否合法 先删除原有secret,再配置新的secret # 删除原tls类型的secret kubectl -n istio-system d…...

SpringBoot 统一后端返回格式、处理全局异常
文章目录 引言I 统一标准格式1.1 定义返回标准格式1.2 定义状态码1.3 返回数据模型1.4 枚举定义1.5 Json序列化处理1.6 获取枚举字典II 处理全局异常2.1 全局异常处理器2.2 自定义异常2.3 请求数据模型III 预备知识:注解3.1 JsonInclude3.2 JsonIgnoreProperties...
C++学习基础版(一)
目录 一、C入门 1、C和C的区别 2、解读C程序 3、命名空间 4、输入输出 (1)cout输出流 (2)endl操纵符 (3)cin输入流 二、C表达式和控制语句 1、数据机构 特别:布尔类型bool 2、算数运…...

Rust 双向链表 LinkedList 和安全删除元素的方法
一、LinkedList 基本用法 在Rust中,LinkedList 是标准库中 std::collections 模块提供的一个双向链表实现。这个双向链表在每个节点中都保存了其前一个和后一个节点的引用,允许在链表的任一端进行有效的添加和移除操作。 以下是一个简单的示例…...

Android 开发中 Gradle 使用详解:构建、配置与优化技巧
文章目录 1. 基本概念2. 配置构建脚本2.1 项目级构建脚本2.2 模块级构建脚本 3. 自定义构建变体和应用 flavorDimensions4. 多模块项目4.1 创建模块4.2 配置模块依赖 5. 使用 Gradle 插件6. 使用 Gradle 命令 Gradle 是一种先进的构建工具,它被广泛应用于 Android 开…...
聚道云助力:易快报CDP无缝对接,登录同步一步到位!
一、客户介绍 某企业咨询有限公司是一家专注于为企业提供全方位、高质量咨询服务的领先机构。该公司致力于将先进的管理理念和实践经验与企业实际需求相结合,助力企业实现可持续发展。无论是战略规划、组织优化、人力资源管理,还是市场营销、财务管理等…...

Java解决幸运数字
Java解决幸运数字 01 题目 哈沙德数是指在某个固定的进位制当中,可以被各位数字之和整 除的正整数。 例如 126 是十进制下的一个哈沙德数,因为 (126)10 mod (1 2 6) 0; 126 也是8进制下的哈沙德 数,因为(126)10 (176)8,(126)10…...

将一个nextjs项目部署到vercel
注:下面均为AI创作(本人已验证该流程可行) 将一个 Next.js 项目部署到 Vercel 是一个相对直接的过程,因为 Vercel 是由同一个团队开发的,专门为 Next.js 优化。以下是部署一个 Next.js 项目到 Vercel 的基本步骤&…...
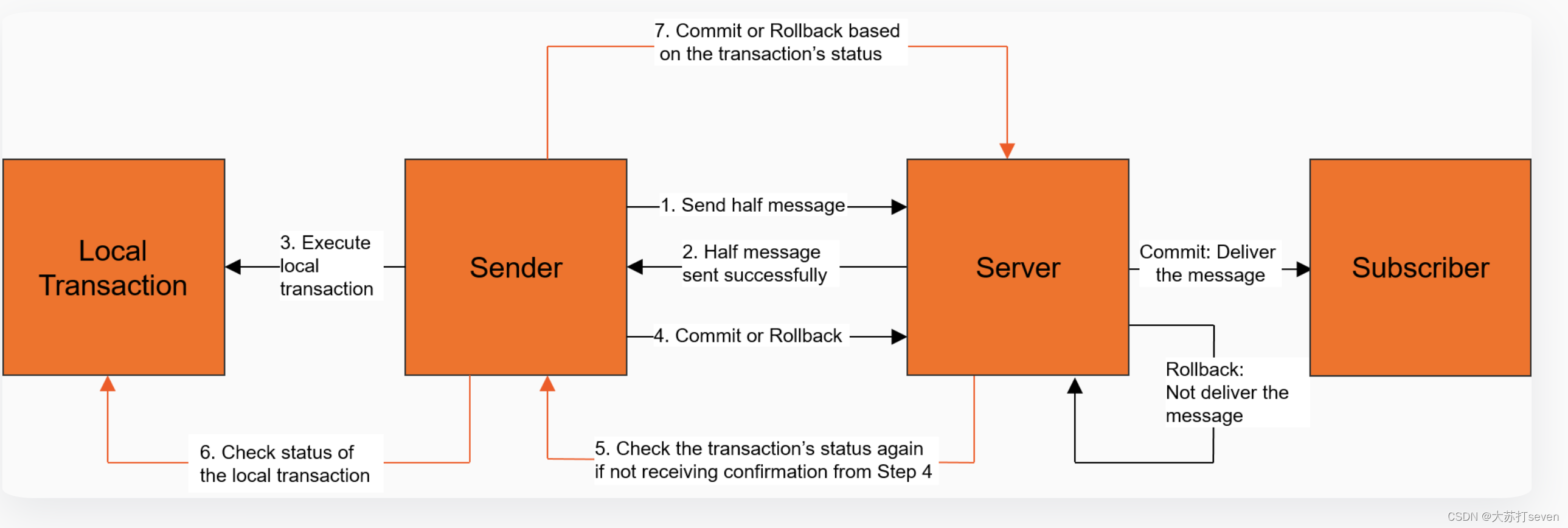
RocketMQ学习笔记:分布式事务
这是本人学习的总结,主要学习资料如下 马士兵教育rocketMq官方文档 目录 1、分布式事务的难题2、解决方式2.1、半事务消息和事务回查2.2、代码样例2.2.1、TransactionListener2.2.2、TransactionMQProducer2.2.3、MessageListenerConcurrently2.2.4、流程图 1、分布…...

单臂路由和三层交换机
目录 一.单臂路由 1.单臂路由的工作原理 2.单臂路由的配置 2.1画出拓扑图 2.2配置PC 2.3配置交换机 2.4配置路由器 2.5测试 二.三层交换机 1.三层交换机的概述 2.三层交换机的配置 2.1画出拓扑图 2.2配置PC 2.3配置二层交换机 2.4配置三层交换机 2.5测试 3.拓展 三.总结 一.…...
红岩思维导图的制作软件,分享4款热门的!
红岩思维导图的制作软件,分享4款热门的! 在当今信息爆炸的时代,思维导图作为一种有效的知识整理和思维拓展工具,受到了广大用户的青睐。红岩思维导图以其独特的风格和实用性,成为了许多人学习和工作中的得力助手。那么…...

es 集群开机自动启动
前面搭建了 es 集群,但是每次机器重启 都需要手动启动,很麻烦,所以这里介绍一下开机自动启动 首先使用 root 用户 es : 执行以下命令 vim /etc/init.d/elasticsearch 将以下内容 cv 进去 #!/bin/bash #chkconfig: 345 63 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
