算法系列--动态规划--背包问题(1)--01背包详解
💕"趁着年轻,做一些比较cool的事情"💕
作者:Mylvzi
文章主要内容:算法系列–动态规划–背包问题(1)–01背包详解
大家好,今天为大家带来的是
算法系列--动态规划--背包问题(1)--01背包详解
一.什么是背包问题
背包问题是动态规划中经典的一类问题,经常在笔试面试中出现,是非常具有区分度的题目
背包问题的种类很多,变式多,也就使得背包问题的难度一般都很高,而01背包问题属于其中最基础,可以当做思考模版的题目,下面就来讲解–01背包问题
前情提示:如果你没有动态规划的基础,还是尽量不要通过背包问题入门,先去做上几十到动态规划的题目再来学习背包问题
二.01背包问题
链接:
01背包问题
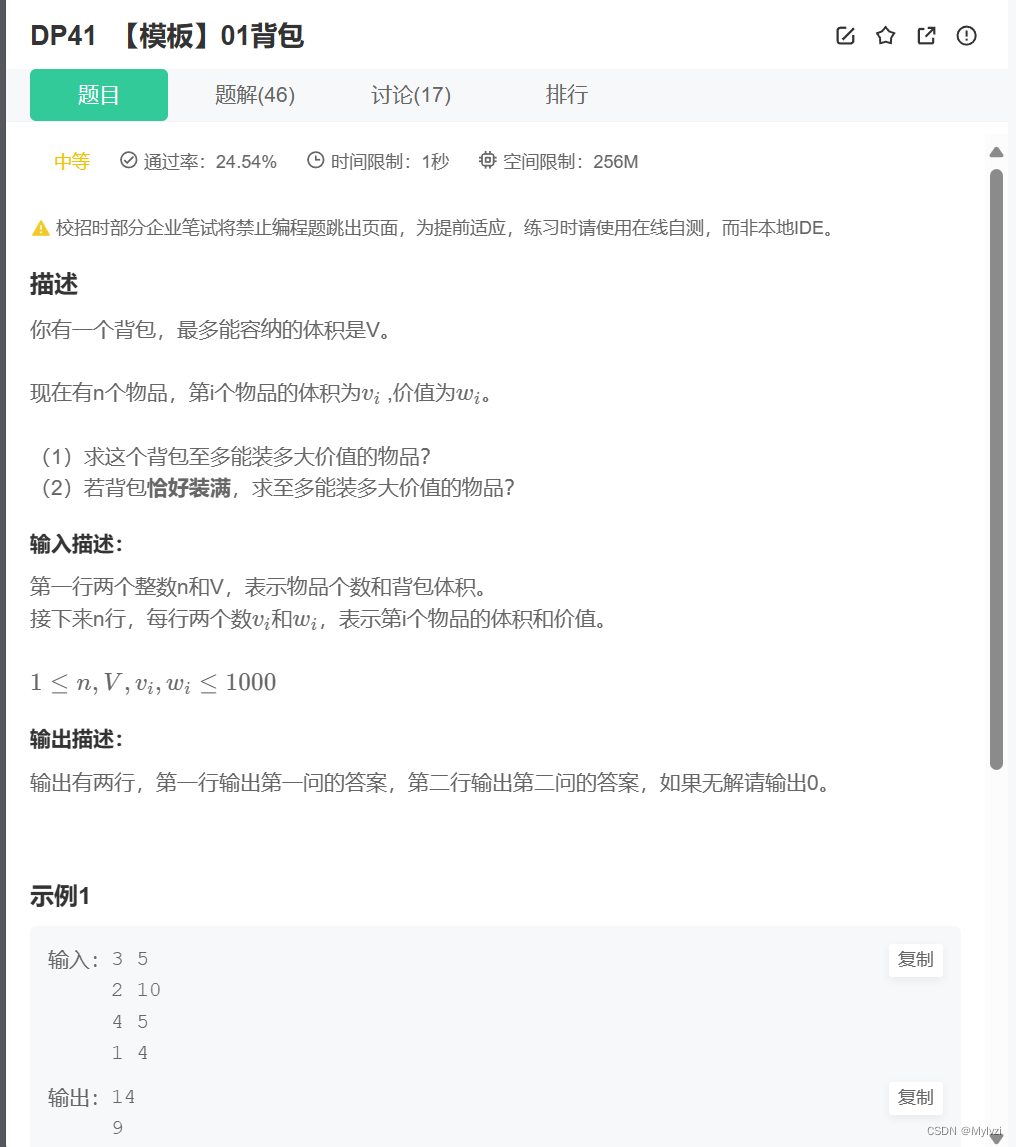
分析:
首先要明确这道题目一共有两问,第一问求的是在不超过背包限制的前提下,可以得到的最大价值
,第二问求的是在刚好装满背包的情况下,可以得到的最大价值
第一问:求这个背包至多能装多大价值的物品?
我们先来模拟一下背包问题的执行过程,其实就是从所有物品中选择合适的物品填入背包,来实现价值的最大化,在选物品时我们是可以任意选择的,这不就类似于在任意的子序列中,选出最大xxxx的问题么?
好了,相信大家也能分析到这里,说:这不就是一个简单的子序列问题么,这有啥难得,于是兴致勃勃的写下状态表示
dp[i]:表示在[1,i]之间的所有物品中,可以实现的最大价值物品的价值
(注:下标我们从1开始是因为这是dp问题常用的一种初始化dp表的方式)
但是我们在填i位置的值时,需要考虑此时背包容量对我们装填的影响(比如如果背包的容量很小,只有1,而我们i物品的体积是99,肯定无法装进去)
所以我们还需要一个状态来表示背包体积,也就是每走到一个物品都要保证符合容量大小,于是状态表示如下:
dp[i][j]:在[1,i]之间的所有物品中,体积不超过j,可以实现的最大价值物品的价值
我们可以验证一下这个状态表示能否返回最终的结果呢?可以,dp[n][V]就表示在所给定的n个物品中,体积不超过背包的最大体积V,选择可以实现最大价值的物品的价值
接下来就来推到状态转移方程:
状态转移方程一般就是根据最后一个位置的状态去讨论,在本题中,分类讨论的依据就是包不包括最后一个物品
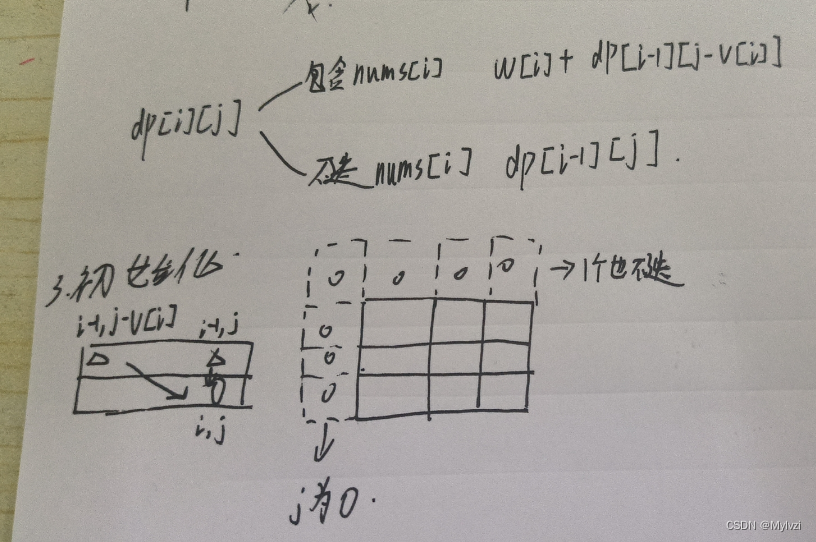
注意:选nums[i]这种情况不是一定能实现的,需要满足此时的背包体积大于第i个物品的体积,也就是需要满足j - v[i] >= 0
返回值:dp[n][V]
以上就是第一问的详细分析过程
第二问:若背包恰好装满,求至多能装多大价值的物品?
相较于第一问多了体积的限制,必须要满足体积的前提下实现价值的最大化,但是大致的思路和第一问很像,只需要在第一问的基础上做出一些改变即可:
dp[i][j]:表示在[0,i]区间内的物品,在体积为j的前提下,可以实现的最大价值
状态转移方程
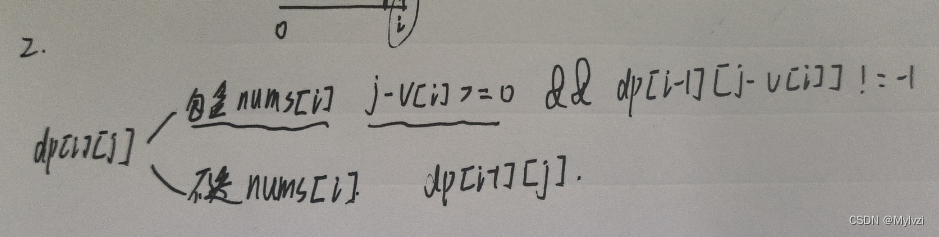
这里多了个限制条件dp[i - 1][j - v[i]] != -1,还是根据题目要求得来的,要考虑一种特殊情况,也就是在[0,i]区间内的物品根本无法组合成体积为j的情况(这也是会存在的),要想i位置存在价值,必须保证i-1位置刚好能够实现j-v[i]的体积
初始化相较于第一问也有所不同,具体来说需要把dp表的第一行初始化为-1(除了dp[0][0]),第一行代表不选择任何物品,也就无法构成满足j体积这个条件,我们将其设置为-1
之所以设置为-1是为了和dp[0][0] = 0这种情况作区分
代码:
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {static int N = 1010;public static void main(String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt(), V = in.nextInt();// 获取物品数目和背包体积// 处理第一问int[] v = new int[N],w = new int[N];// 存储物品的体积和价值for(int i = 1; i <= n; i++) {// 输入数值v[i] = in.nextInt(); w[i] = in.nextInt();}int[][] dp = new int[N][N];for(int i = 1; i <= n; i++) {for(int j = 1; j <= V; j++) {dp[i][j] = dp[i - 1][j];if(j - v[i] >= 0) dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - v[i]] + w[i]);}}System.out.println(dp[n][V]);// 处理第二问dp = new int[N][N];for(int j = 1; j <= V; j++) {// 初始化dp[0][j] = -1;}for(int i = 1; i <= n; i++) {for(int j = 1; j <= V; j++) {dp[i][j] = dp[i - 1][j];if(j - v[i] >= 0 && dp[i - 1][j - v[i]] != -1)dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - v[i]] + w[i]);}}System.out.println(dp[n][V] == -1 ? 0 : dp[n][V]);}
}
上述解法的空间复杂度是很高的,我们开辟的dp表是一个N*N的,下面介绍使用滚动数组实现空间优化
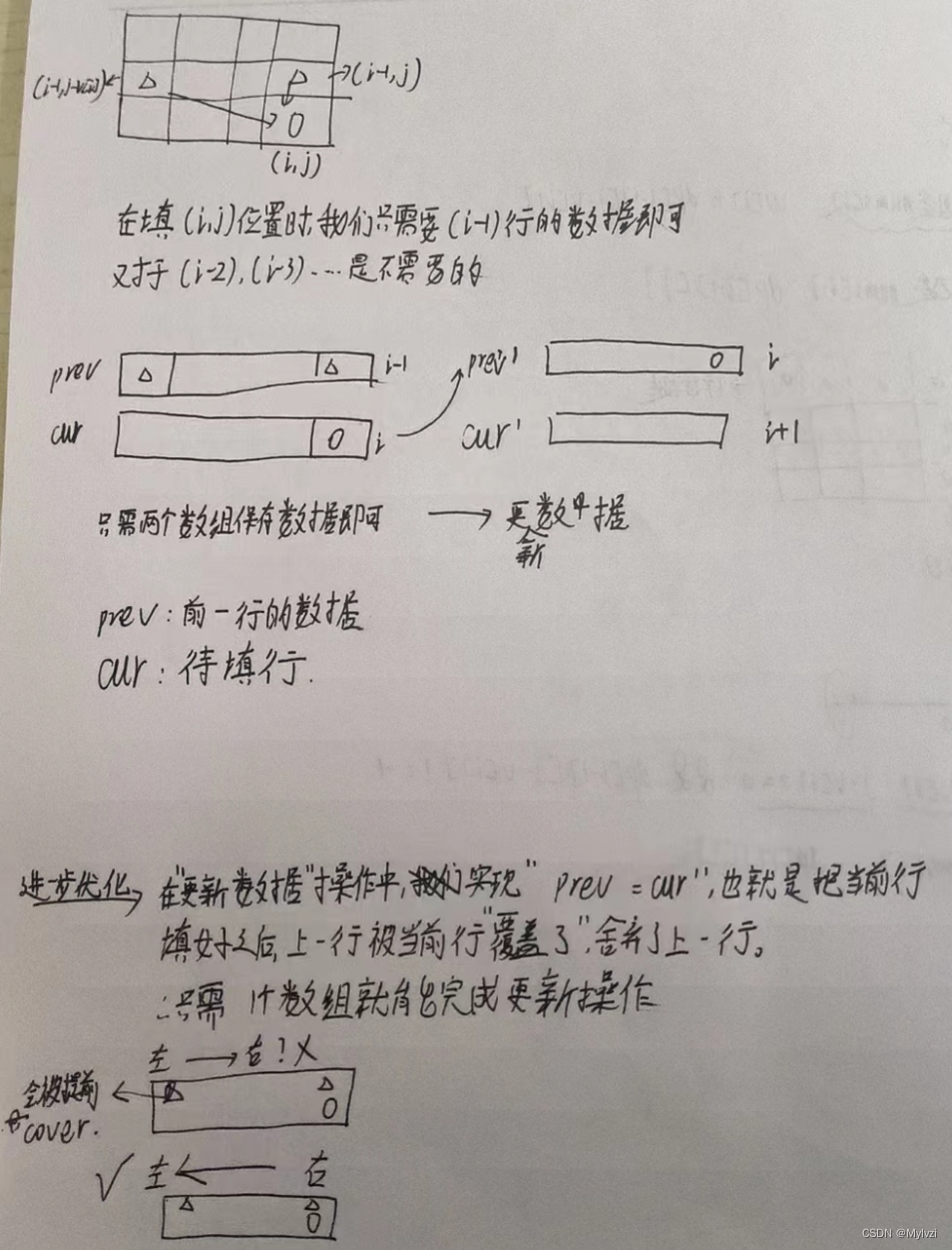
空间优化之后的代码:
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {static int N = 1010;public static void main(String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt(), V = in.nextInt();// 获取物品数目和背包体积// 处理第一问int[] v = new int[N],w = new int[N];// 存储物品的体积和价值for(int i = 1; i <= n; i++) {// 输入数值v[i] = in.nextInt(); w[i] = in.nextInt();}int[] dp = new int[N];for(int i = 1; i <= n; i++) for(int j = V; j >= v[i]; j--) dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);System.out.println(dp[V]);// 处理第二问dp = new int[N];for(int j = 1; j <= V; j++) dp[j] = -1;// 初始化for(int i = 1; i <= n; i++) for(int j = V; j >= v[i]; j--) if(j - v[i] >= 0 && dp[j - v[i]] != -1)dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);System.out.println(dp[V] == -1 ? 0 : dp[V]);}
}
总结:本文的核心要点
- 什么是背包问题
- 01背包问题详解
- 背包问题的空间优化(滚动数组)
相关文章:

算法系列--动态规划--背包问题(1)--01背包详解
💕"趁着年轻,做一些比较cool的事情"💕 作者:Mylvzi 文章主要内容:算法系列–动态规划–背包问题(1)–01背包详解 大家好,今天为大家带来的是算法系列--动态规划--背包问题(1)--01背包详解 一.什么是背包问题 背包问题…...

【KB】通过Karabiner-Elements实现 optionTAB与 commandTAB 对调/映射 win 的 altTAB 习惯
学习Karabiner-Elements的第一个 demo,因为推荐的例子中过多参数,这是一个简化版。 需求:对调 optionTAB与 commandTAB,然后安装 altTAB 软件,恢复win切换任务的使用习惯。 {"description": "Change ta…...

nvm node包管理工具
下载地址:版本 1.1.9 CoreyButler/NVM-Windows (github.com) 使用nvm -v 检查安装是否成功。 常用命令 # 安装nodjs版本 nvm install 10.16.3nvm install 14.15.4# 切换,使用nodejs nvm use 10.16.3 ## nvm use 报错,1).使用管理员打开…...
程序员如何兼职赚小钱?
程序员由于有技术和手艺其实兼职赚钱的路子还是挺多的,只要你有足够的时间。 1. 做外包 这是比较传统的方式,甲方在一些众包平台上发布开发任务,你可以抢这个任务,但是价格都比较便宜。 任务比较多的平台: 猪八戒、一品威客、开…...
奥比中光深度相机(一):环境配置
文章目录 奥比中光深度相机(一):环境配置简介电脑环境SDK配置步骤安装环境依赖填写路径,点击Configure选择Visual studio点击Generate完成基于Python的SDK配置方法一:使用Cmake直接打开方法二:通过源文件打…...

API网关-Apisix路由配置教程(数据编辑器方式)
文章目录 前言一、端口修改1. apisix 端口修改2. dashboard 端口修改3. 登录密码修改 二、常用插件介绍1. 常用转换插件1.1 proxy-rewrite插件1.1.1 属性字段1.1.2 配置示例 2. 常用认证插件2.1 key-auth插件2.1.1 消费者端字段2.1.2 路由端字段2.1.3 配置示例 2.2 basic-auth插…...
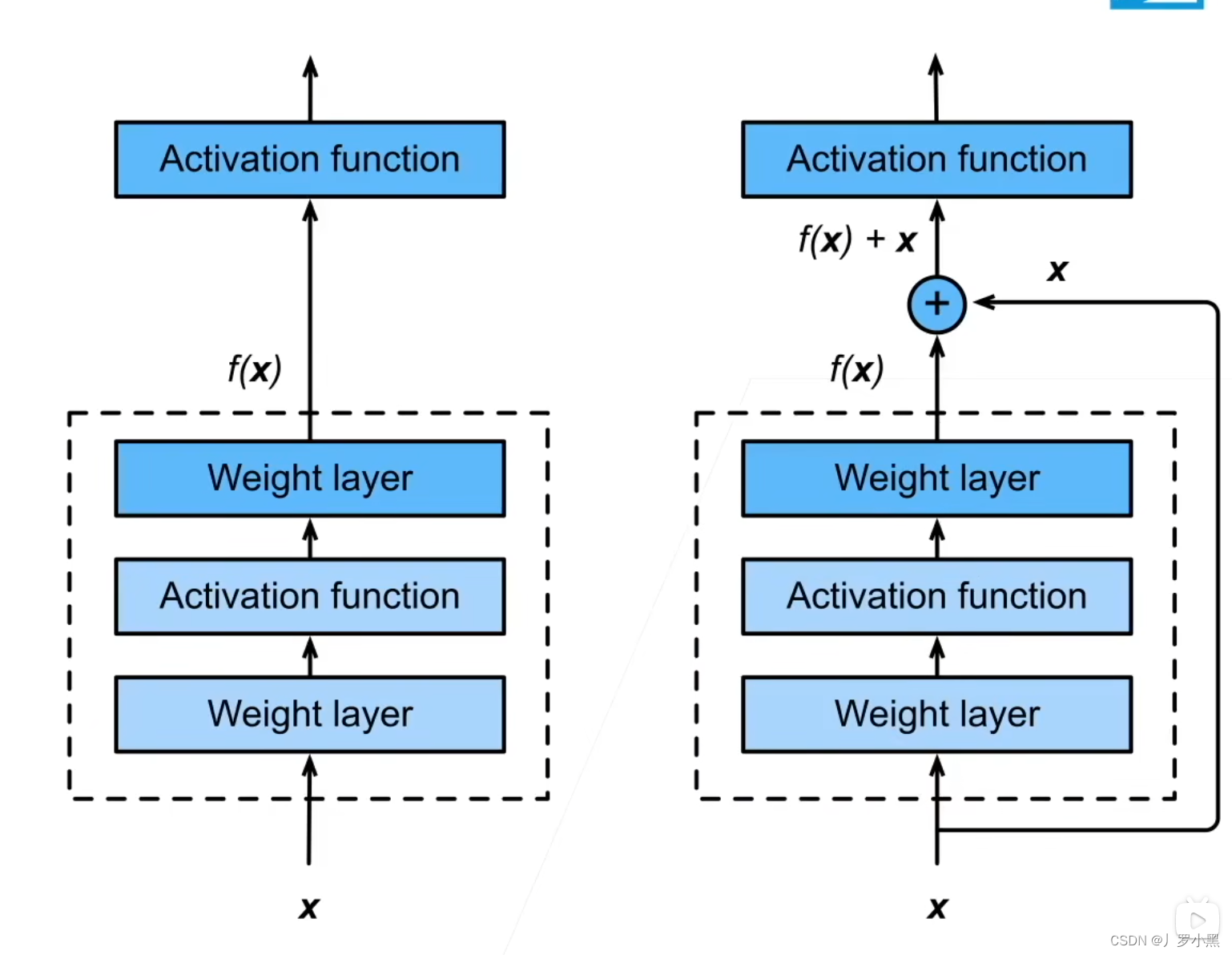
Transformer的前世今生 day10(Transformer编码器
前情提要 ResNet(残差网络) 由于我们加更多层,更复杂的模型并不总会改进精度,可能会让模型与真实值越来越远,如下: 我们想要实现,加上一个层把并不会让模型变复杂,即没有它也没关系…...

【c++模板】泛型编程(你真的懂模版特化、分离编译和非类型参数吗)
🪐🪐🪐欢迎来到程序员餐厅💫💫💫 今日主菜:模板 主厨:邪王真眼 主厨的主页:Chef‘s blog 所属专栏:c大冒险 总有光环在陨落,总有新星在…...
)
力扣1----10(更新)
1. 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按…...

[Qt] QString::fromLocal8Bit 的使用误区
QString::fromLocal8Bit 是一个平台相关的函数。默认情况下在 Windows 下 就是 gbk 转 utf-8 ,在 Linux就应该是无事发生。因为Linux平台默认的编码方式就是 utf-8 可以通过 void QTextCodec::setCodecForLocale(QTextCodec *c)来修改 Qt默认的编码方式。如下 第一输出乱码的…...

什么是RabbitMQ的死信队列
RabbitMQ的死信队列(Dead Letter Queue,简称DLQ)是一种用于处理消息失败或无法路由的消息的机制。它允许将无法被正常消费的消息重新路由到另一个队列,以便稍后进行进一步处理、分析或排查问题。 当消息对立里面的消息出现以下几…...

力扣面试150 删除有序数组中的重复项 双指针
Problem: 26. 删除有序数组中的重复项 思路 👩🏫 三叶题解 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( 1 ) O(1) O(1) Code class Solution {public int removeDuplicates(int[] nums) {int j 0, n nums.length;for(int i 0;…...
政安晨:【深度学习实践】【使用 TensorFlow 和 Keras 为结构化数据构建和训练神经网络】(二)—— 深度神经网络
政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: TensorFlow与Keras实战演绎 希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正! 概述 深度神经网络(Deep Neural Network…...
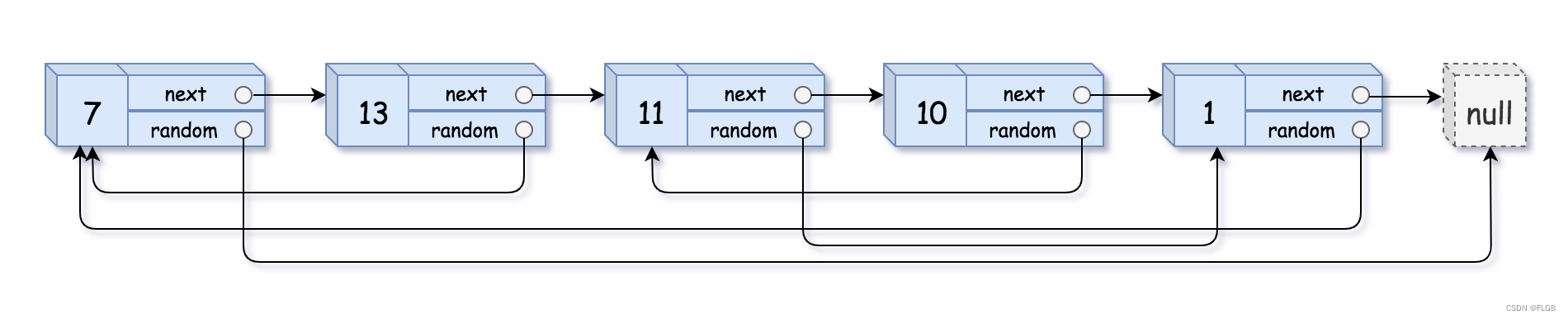
【链表】Leetcode 138. 随机链表的复制【中等】
随机链表的复制 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点…...
第2章课后习题答案)
【计算机网络教程】(第六版)第2章课后习题答案
第二章 2-012-022-032-042-062-072-082-092-102-112-122-132-142-152-16 2-01 物理层要解决哪些问题?物理层的主要特点是什么? 答: 物理层要解决的主要问题: (1)物理层要尽可能地屏蔽掉物理设备和传输媒体&…...

抖音电商“达人客服”产品上线啦!超多作者邀你一起“321上客服”!
有问题别自己克服,来抖音电商找“达人客服” 当代年轻人购物,正在从机智省变成理智购。越来越多的人在达人直播间购物,看重的不止是优惠力度,还有服务保障。 为了帮助达人更好地服务用户,抖音电商上线了「达人客服」…...

华为防火墙二层墙(VAN/SVI/单臂路由)
二层墙只能做地址池形式的NAT。 交换机安全策略防火墙二层墙 路由器安全策略防火墙三层墙 交换机的光口是不能直接插线的,光模块,包括进和出 长距离:单模 短距离:多模 防火墙自身的ping流量需要单独配置...
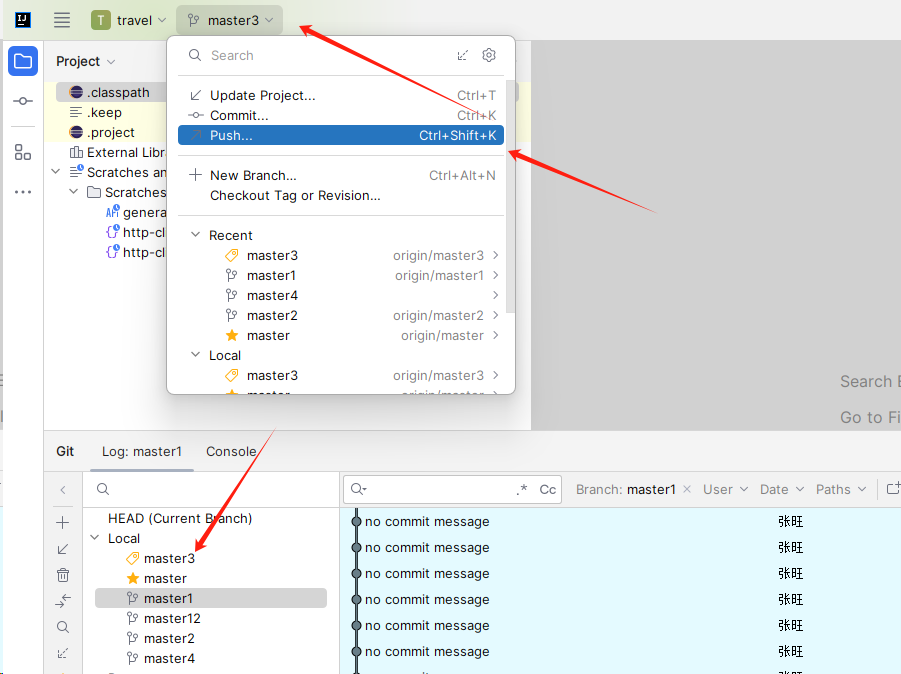
idea使用git笔记
1.创建分支和切换分支 创建分支 切换分支 2.把新创建的分支提交到远程服务器上(注:如果没有提交的,随便找个文件修改再提交) (1)切换到要提交的分支,add (2)commit (3)push 3.在自己分支修改代码及提交到自己的远…...

智慧校园数据可视化有什么好处?怎么推进数字化校园方案?
在当今数字化时代,越来越多学校开始实施智慧校园计划,旨在为学生和教师提供更高效、便捷的学习和教学环境。智慧校园运用互联网、大数据、人工智能等技术,对校园内各信息进行收集、整合、分析和应用,实现教学、管理、服务等多方面…...
求数列和)
如何利用python编写函数fn(a,n)求数列和
1 问题 编写函数fn(a,n) 求aaaaaa⋯aa⋯aa(n个a)之和,fn须返回的是数列和,输入正整数a和n的值(两个值都不超过9),并输出fn(a,n)的结果值。 2 方法 运用def 定义函数和for 循环递归方法: 先定义fn(a,n)函数;…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

