数值分析复习:逼近理论的应用——最小二乘问题、解超定、欠定方程组
文章目录
- 逼近理论的应用——最小二乘问题、解超定、欠定方程组
- 离散平方逼近
- 最小二乘解
本篇文章适合个人复习翻阅,不建议新手入门使用
本专栏:数值分析复习 的前置知识主要有:数学分析、高等代数、泛函分析
逼近理论的应用——最小二乘问题、解超定、欠定方程组
离散平方逼近
设全空间 X = R n X=\mathbb{R}^n X=Rn, 在 R n \mathbb{R}_n Rn 中取 m < n m<n m<n 个线性无关的向量 ( X 1 , … , X m ) (X_1,\dots,X_m) (X1,…,Xm),令 M = s p a n { X 1 , … , X m } M=span\{X_1,\dots,X_m\} M=span{X1,…,Xm},则对任意 Y ∈ X \ M Y\in X\backslash M Y∈X\M, M M M 中存在唯一的最佳逼近元 X ∗ = ∑ i = 1 m c i X i X^*=\sum\limits_{i=1}^mc_iX_i X∗=i=1∑mciXi,其满足以下法方程组
∑ i = 1 m < X i , X j > c i = < Y , X j > \sum\limits_{i=1}^m<X_i,X_j>c_i=<Y,X_j> i=1∑m<Xi,Xj>ci=<Y,Xj>若设 A = [ X 1 , … , X m ] , C = [ c 1 , … , c m ] T A=[X_1,\dots,X_m],C=[c_1,\dots,c_m]^T A=[X1,…,Xm],C=[c1,…,cm]T,则方程组等效于
A T A C = A T Y A^TAC=A^TY ATAC=ATY
最小二乘解
求如下的最小化问题的解
x ∈ R n , s . t . min ∣ ∣ A x − b ∣ ∣ 2 x\in \mathbb{R}^n,s.t.\min||Ax-b||_2 x∈Rn,s.t.min∣∣Ax−b∣∣2由离散平方逼近的理论,其解满足
A T A x = A T b A^TAx=A^Tb ATAx=ATb
应用:求解超定、欠定方程组
我们把线性方程组 A x = b Ax=b Ax=b 中,
未知数多于方程个数的方程组称为欠定方程组,
未知数多于方程个数且有矛盾方程的方程组称为超定方程组。
欠定方程组一般有多个解,超定方程组一般无解,故在工程上常用1范数或2范数意义下的最佳逼近解来作为解,即上述的最小二乘解
x ∈ R n , s . t . min ∣ ∣ A x − b ∣ ∣ 2 x\in \mathbb{R}^n,s.t.\min||Ax-b||_2 x∈Rn,s.t.min∣∣Ax−b∣∣2其解满足
A T A x = A T b A^TAx=A^Tb ATAx=ATb
参考书籍:《数值分析》李庆扬 王能超 易大义 编
相关文章:

数值分析复习:逼近理论的应用——最小二乘问题、解超定、欠定方程组
文章目录 逼近理论的应用——最小二乘问题、解超定、欠定方程组离散平方逼近最小二乘解 本篇文章适合个人复习翻阅,不建议新手入门使用 本专栏:数值分析复习 的前置知识主要有:数学分析、高等代数、泛函分析 逼近理论的应用——最小二乘问题、…...

设计模式-设配器模式
目录 🎊1.适配器模式介绍 🎃2.适配器类型 🎏3.接口适配器 🎐4.类的适配器 🎎5.优缺点 1.适配器模式介绍 适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁。这种类型的设…...
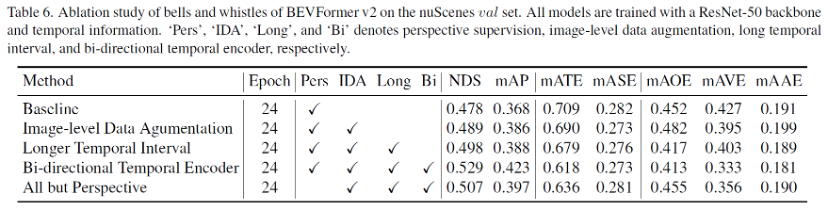
BEVFormer v2论文阅读
摘要 本文工作 提出了一种具有透视监督(perspective supervision)的新型鸟瞰(BEV)检测器,该检测器收敛速度更快,更适合现代图像骨干。现有的最先进的BEV检测器通常与VovNet等特定深度预训练的主干相连,阻碍了蓬勃发展…...
)
FFMPEG C++封装(二)
4 详细设计 这章是FFMPEG C封装库的详细设计。 4.1 Init 该模块初始化FFMPEG库。 4.1.1 Init定义 namespace media { namespace sdk { void MEDIASDK_EXPORT Init(); } }函数说明: Init 初始化FFMPEG库,该函数可调用多次。 4.1.2 Init实现 name…...
使用unplugin-auto-import页面不引入api飘红
解决方案:. tsconfig.json文件夹加上 {"compilerOptions": {"target": "ES2020","useDefineForClassFields": true,"module": "ESNext","lib": ["ES2020", "DOM", &q…...

八大技术趋势案例(虚拟现实增强现实)
科技巨变,未来已来,八大技术趋势引领数字化时代。信息技术的迅猛发展,深刻改变了我们的生活、工作和生产方式。人工智能、物联网、云计算、大数据、虚拟现实、增强现实、区块链、量子计算等新兴技术在各行各业得到广泛应用,为各个领域带来了新的活力和变革。 为了更好地了解…...

Vue实现SQL语句关键字高亮显示?
SQL关键字高亮 要在Vue中实现SQL语句中关键字的高亮显示,你可以使用类似的方法,但是你需要根据SQL语法的特点来解析并高亮显示关键字。以下是一个示例代码,演示了如何在Vue中实现SQL语句关键字的高亮显示。 <template><div><…...
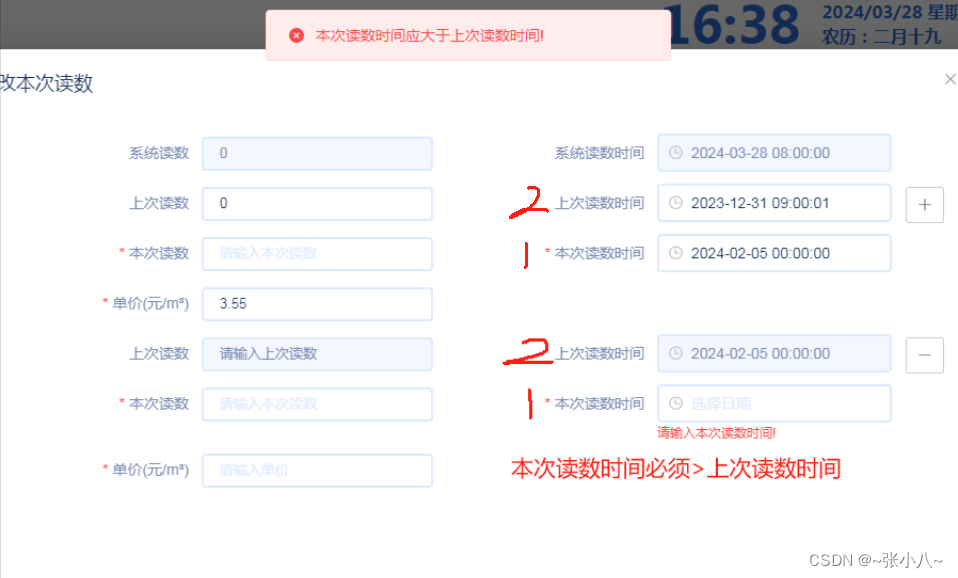
开始时间大于结束时间
1.dom中代码,监听所选日期值的变化,并把需要比较的时间字段作为参数传到监听方法中, <el-form-item label"起始日期" prop"startTime"><el-date-picker clearable size"small":disabled"isDisa…...

Java中 List 集合,通过 Stream 流进行排序总结
一、数据准备 public class OrderTest {private String channelCode;private BigDecimal rate;// 省略 getter、setter、toString()、constructor }List<OrderTest> orderTestList new ArrayList<>();OrderTest z09 new OrderTest("Z09", new BigDeci…...

1688中国站按关键字搜索工厂数据 API
公共参数 名称类型必须描述keyString是申请免费调用key(必须以GET方式拼接在URL中)secretString是调用密钥api_nameString是API接口名称(包括在请求地址中)[item_search,item_get,item_search_shop等]cacheString否[yes,no]默认y…...
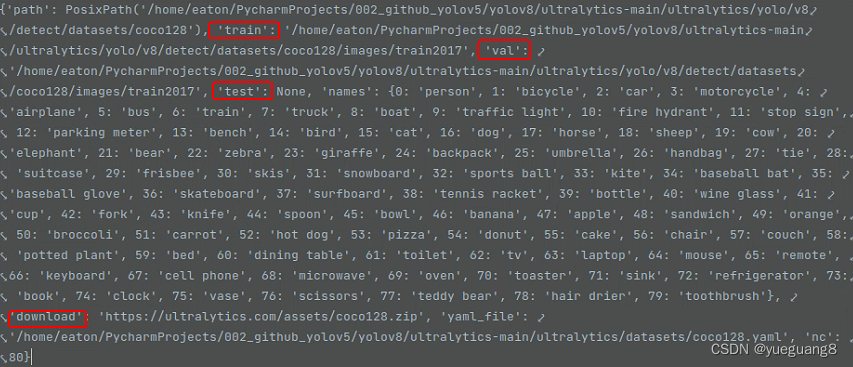
YOLOV8逐步分解(2)_DetectionTrainer类初始化过程
接上篇文章yolov8逐步分解(1)--默认参数&超参配置文件加载继续讲解。 1. 默认配置文件加载完成后,创建对象trainer时,需要从默认配置中获取类DetectionTrainer初始化所需的参数args,如下所示 def train(cfgDEFAULT_CFG, use_pythonFalse…...

Java是用什么语言写的?PHP呢?
Java底层是C语言。 Sun公司研发人员根据嵌入式软件的要求,对C进行了改造,去除了留在C的一些不太实用及影响安全的成分,并结合嵌入式系统的实时性要求,开发了一种称为Oak的面向对象语言。而后,经过迭代更新,…...
SpringBoot Redis的使用
官方文档: 官方文档:Spring Data Redis :: Spring Data Redis 和jedis一样,SpringBoot Redis 也可以让我在Java代码中使用redis,同样也是通过引入maven依赖的形式。 加速访问github: 使用steam可以免费加速访问github Spring…...

数据仓库——维度表特性
企业信息化工厂 数据集市中的一致性,由于企业信息化工厂的数据集市是从集成仓库中获得信息的,因此至少从维度建模的角度来看,一致性维护的问题减少了。尽管合并不同数据源的问题依然在,但是负担主要在设计者身上。尽管压力降低了…...
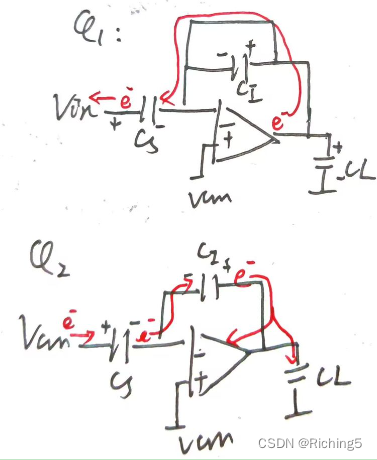
从电荷角度理解开关电容中的电荷守恒
目录 一些铺垫电容的电荷量的解释电荷流入流出对节点电压的影响 从电荷角度理解开关电容加法器中的电荷守恒以开关电容积分器为例说明什么样的节点是电荷守恒 一些铺垫 电容的电荷量的解释 对于一个1F的电容,当它的压差为1V时,它所携带的电荷量是QCU1库…...

1.7.1 python 作业 15道
1、求出1 / 1 1 / 3 1 / 5……1 / 99的和 (1分之一1分之三1分支5....) sum0 for i in range(1,100,2): sum 1/i sum; print(sum) 2、用循环语句,计算2 - 10之间整数的循环相乘的值 (2*3*4*5....10) sum 1 for i in range(2,11): sum sum *…...

synchronized 和 ReentrantLock 的区别是什么
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:synchronized 和 ReentrantLock 的区别是什么 1. 获取锁的方式 synchronized:synchronized的锁获取是隐式的。当线程进入synchronized修饰的代码…...

大话设计模式之迪米特法则
迪米特法则,也称为最少知识原则(Law of Demeter),是面向对象设计中的一个重要原则,其核心思想是降低耦合度、减少对象之间的依赖关系,从而使系统更加灵活、易于维护和扩展。 根据迪米特法则,一…...

KSD测试系统使用方法和注意事项
①下载链接在最顶部; ②安装方法:应该先将测试设备绑定在假人身上,测试设备不能过度往下拉,传感器绑在脖子上,切记最后才开传感器开关!!!开传感器后3秒内不要碰测试设备衣服&#x…...

IT服务营销管理案例分析题
习题一 企业随着业务的蓬勃发展,所投入的基础设施资源不断增加。企业员工数倍数增长,办公场地、办公环境等要求也越来越高。 可是该企业的IT部门人员短缺,对IT管理还处于被动的“救火”阶段,每天至少15个突发故障,故障…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
