图论最短路径以及floyd算法的MATLAB实现
图论是数学的一个分支,起源于18世纪。1736年,数学家欧拉通过解决“哥尼斯堡七桥问题”,将问题抽象成点和线的关系,并通过理论分析得出结论,这个过程标志着图论的产生,欧拉也因此被称为“图论之父”。图论研究的是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,其中点代表事物,连接两点的线表示相应两个事物间具有这种关系。
一、无向图和有向图在图论中都是重要的概念,它们之间存在显著的区别。
首先,从定义上来看,无向图是一种由节点和边组成的数据结构,边没有方向性,也就是说,如果存在一条边(u, v),那么从u到v和从v到u都是可以的。这种图通常用来表示双向关系,如社交网络中的友谊关系。而有向图则是一种具有方向性的图,由一组顶点和一组有方向的边组成,每条方向的边都连着一对有序的顶点。在有向图中,如果存在一条边(u, v),那么只能从u到v,但不一定能从v到u。
此外,从应用角度来看,无向图主要用于表示双向关系,如社交网络、传输网络等,以及用于搜索最短路径等问题。而有向图则更多地用于表示具有方向性的关系,如流程、路径规划等。
二、在图论中,最短路径问题是一个经典问题,它涉及从图中某一顶点(源点)出发,到达另一顶点(终点)的所有路径中,寻找各边权值之和最小的路径,这种路径称为最短路径。
最短路径问题可以分为两类:单源最短路径问题和多源最短路径问题。单源最短路径问题是求单个顶点和其他所有顶点的最短路径,而多源最短路径问题则是求所有顶点相互之间的最短路径。对于最短路径问题,有多种算法可以用来求解,包括但不限于:
- Dijkstra算法:这是最短路径算法中最常用的一种。它基于贪心策略,通过逐步扩展路径来求解最短路径。算法的基本思想是,从一个起始顶点开始,逐步扩展到其他顶点,每次选择当前路径中距离起始顶点最近的顶点进行扩展,直到扩展到目标顶点或者所有顶点都被扩展完毕。
- Bellman-Ford算法:这也是另一种常用的最短路径算法。
- Floyd-Warshall算法:这是一种多源最短路径算法,可以求解图中任意两个顶点之间的最短路径。
以下面问题为例解决问题:

clear;clc;
% 注意Matlab中的图节点要从1开始编号
s = {'v1','v1','v1','v2','v3','v3','v4','v5','v5','v5','v5','v6','v6','v7','v9','v9'};
t = {'v2','v3','v4','v5','v2','v4','v6','v4','v6','v7','v8','v5','v7','v8','v5','v8'};
weight = [6,3,1,1,2,2,10,6,4,3,6,10,2,4,2,3];
%要做出有向图,只需要将graph改为digraph就行了
G= digraph(s,t,weight);%有向图
myplot = plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);%图赋给一个变量
set(gca,'XTick',[],'YTick',[]);
%[p,d] = shortestpath(G,start,end,[‘Method’,algorithm])
% 功能:返回图G中start节点到end节点的最短路径%输入参数:
% (1)G- 输入图 (graph 对象|digraph 对象)
% (2) start 起始的节点%
% (3) end 目标的节点
% (4)[‘Method’,algorithm]是可选的参数,表示计算最短路径的算法。一般我% 们不用手动设置,默认使用的是“auto”,具体可设置的参数见下一页课件。% 输出参数:
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
% (1)P - 最短路径经过的节点
% (2)d - 最短距离
[P,d] = shortestpath(G,'v1','v8')%求v1到v8的最短路径和距离
%在图中高亮出最短路径
highlight(myplot,P,'EdgeColor','red')
%任意两点的最短路径矩阵
D = distances(G)
D(1,8)%v1到v8的最短路径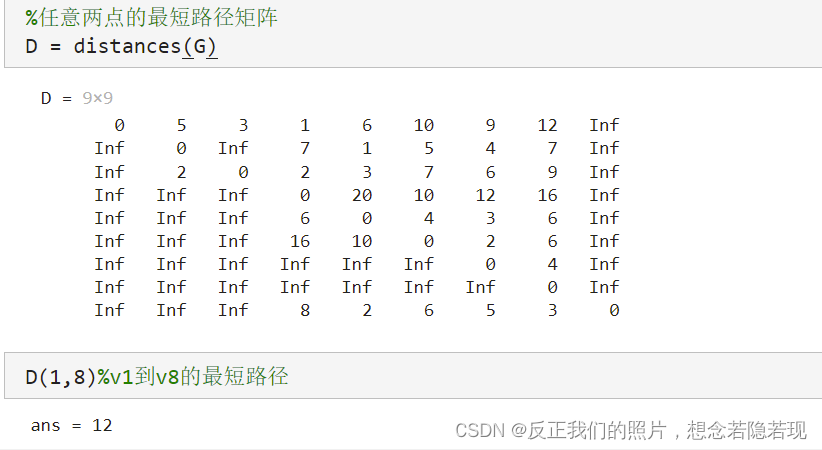 下面是代码floyd算法的MATLAB实现:
下面是代码floyd算法的MATLAB实现:
gg = [0,inf,-2,inf;inf,0,inf,-1; inf,2,0,inf;4,inf,3,0;];
[dist,path] = my_floyd(gg)
function [dist,path] = my_floyd(D)
[r,~]= size(D);
dist = D;
% 下面我们来初始化path矩阵
path = zeros(r);
for j= 1:rpath(:,j) = j; %将第j列的元素变为j
end
for i = 1:rpath(i,i) = -1;%将主对角线元素变为-1
end
for k=1:r%以k为中转for i=1:r %邻接矩阵第i行for j=1:r%邻接矩阵第j列if dist(i,j)>dist(i,k)+dist(k,j)dist(i,j)=dist(i,k)+dist(k,j);path(i,j)=path(i,k);% 起点为i,终点为j的两个节点之间的最短路径要经过的节点更新为path(i,k)% 注意,上面一行语句不能写成path(i,j) = k;endendend
end
end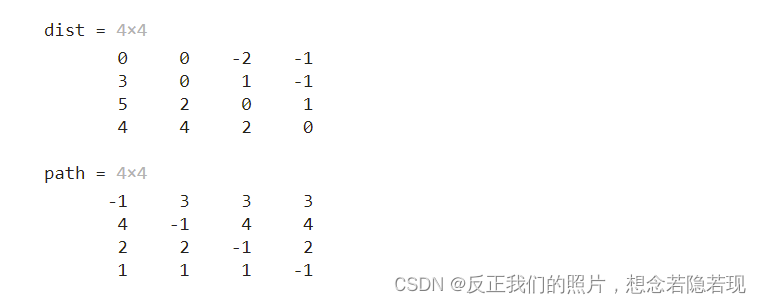 总的来说,图论是一门研究图与网络的理论学科,它在各个领域都发挥着重要的作用,为解决实际问题提供了有力的工具和方法。
总的来说,图论是一门研究图与网络的理论学科,它在各个领域都发挥着重要的作用,为解决实际问题提供了有力的工具和方法。
相关文章:

图论最短路径以及floyd算法的MATLAB实现
图论是数学的一个分支,起源于18世纪。1736年,数学家欧拉通过解决“哥尼斯堡七桥问题”,将问题抽象成点和线的关系,并通过理论分析得出结论,这个过程标志着图论的产生,欧拉也因此被称为“图论之父”。图论研…...
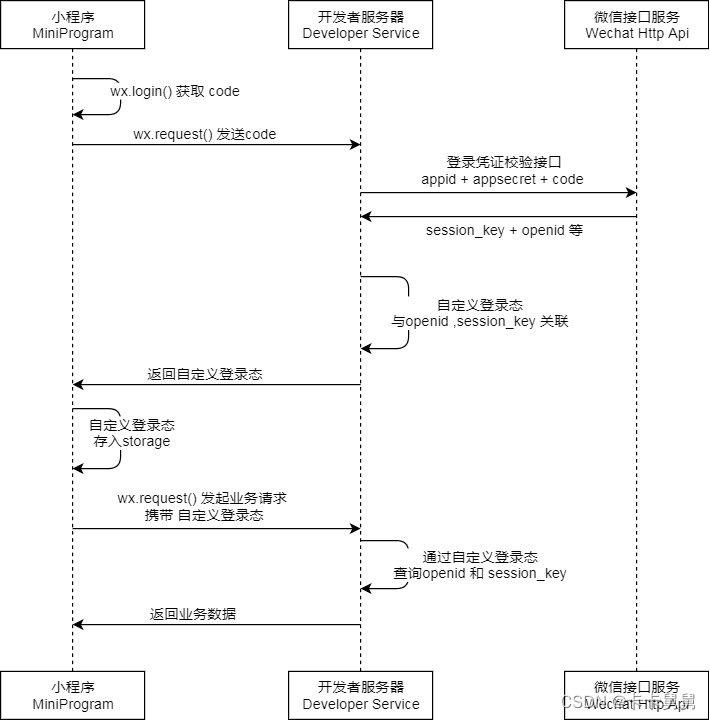
微信小程序 - 登录功能实现
一、认证流程 1. 小程序调用wx.login获取登录认证需要的code,并请求开发者服务器。 2. 开发者服务器根据code,appid, appsecret请求微信接口t获取 openid与session_key ,并生成自己的认证token,并返回给小程序。 3.小程序请求开…...

Python连接MySQL
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、整体思路二、连接流程三、表结构及代码实现 一、整体思路 二、连接流程 三、表结构及代码实现 代码块如下: import pymysqlcon pymysql.connect(h…...

水泊梁山108小酒坛之呼保义宋江
宋江【绰号呼保义、及时雨】字公明,是古典名著《水浒传》中的角色。原为山东郓城县押司,他和晁盖互通往来的事被阎婆惜发现,因此怒杀阎婆惜,逃回家隐藏。后前往清风寨投靠花荣,却被清风寨观灯时遭知寨刘高之妻陷害入狱…...

java.lang.ClassNotFoundException: javafx.application.Application
java8(jdk1.8)到java10(jdk10)中内含有JavaFx 在java11(jdk11)以及以后的版本中剥离出来需要开发者独立下载,另行导入download https://gluonhq.com/products/javafx/java --module-path $FX-P…...
腾讯 tendis 替代 redis linux安装使用
下载地址 Tendis存储版 点击下载 linux 解压 tar -zxvf 安装包.tgz cd 解压安装包/scripts 启动 ./start.sh 停止 ./stop.sh 详细配置 修改 /scripts tendisplus.conf # tendisplus configuration for testing # 绑定本机IIP bind 192.168.31.112 port 51002 #设…...

k8s调优--来自gpt
Kubernetes(K8s)性能调优是一个涉及多个方面的过程,旨在提高集群的效率和响应速度。这包括对节点、Pod、服务、网络和存储等多个层面进行调优。下面我将概述一些常见的Kubernetes性能调优方法: 节点级别的调优: 1.资源分配&…...
HTML5+CSS3小实例:旋转中的视差效果
实例:旋转中的视差效果 技术栈:HTML+CSS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"> <head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scal…...

3-zookeeper之ZAB协议
Zookeeper ZAB协议 概述 ZAB(Zookeeper Automic Broadcast)是一套专门为Zookeeper设计的用于进行原子广播和崩溃恢复的协议ZAB协议主要包含了两个功能 原子广播:保证数据一致性崩溃恢复:保证集群的高可用 ZAB协议本身是基于2PC算法来进行的设计&#…...

如何为企业策划一场XR虚拟直播?
活动年年办,都是老一套,想玩点新花样? 预算有限,但还是想把活动办的逼格高一点? 想通过活动,让更多的人知道自己企业的品牌? 随着AIGC技术的不断演变,企业活动的形式和内容也在不…...

6.3物联网RK3399项目开发实录-驱动开发之I2C 使用(wulianjishu666)
物联网开发源码案例集: 链接:https://pan.baidu.com/s/1kfPDpYZpm_G0GBLAup3KTQ?pwdvgvv I2C 使用 简介 AIO-3399J 开发板上有 9 个片上 I2C 控制器,各个 I2C 的使用情况如下表: 本文主要描述如何在该开发板上配置 I2C。 配置…...

HarmonyOS实战开发-如何构建多种样式弹窗
介绍 本篇Codelab将介绍如何使用弹窗功能,实现四种类型弹窗。分别是:警告弹窗、自定义弹窗、日期滑动选择器弹窗、文本滑动选择器弹窗。需要完成以下功能: 点击左上角返回按钮展示警告弹窗。点击出生日期展示日期滑动选择器弹窗。点击性别展…...

《Effective C++》《构造/析构/赋值运算——7、为多态基类声明virtual析构函数》
文章目录 1、term7:Declare destructors virtual in polymorphic base classes2、总结3、相关面试题3.1 析构函数在什么情况下声明为虚函数 4、参考 1、term7:Declare destructors virtual in polymorphic base classes 带有多态性质的基类应该声明一个virtual析构函数&#x…...

Type-C一分二快充线智能分配方案
随着移动设备的普及和快充技术的迅猛发展,Type-C接口已成为众多手机、平板和笔记本电脑的标配。然而,在日常使用中,我们经常会遇到需要同时为多个设备充电的情况。这时,Type-C一分二快充线就显得尤为重要。为了更好地满足用户的充…...
)
利用python脚本,根据词条爬取百度图片(爬虫)
把广角,换成你的关键词就行 # -*- coding: utf-8 -*- """ Created on Wed Mar 29 10:17:50 2023 author: MatpyMaster """ import requests import os import redef get_images_from_baidu(keyword, page_num, save_dir):header {Us…...
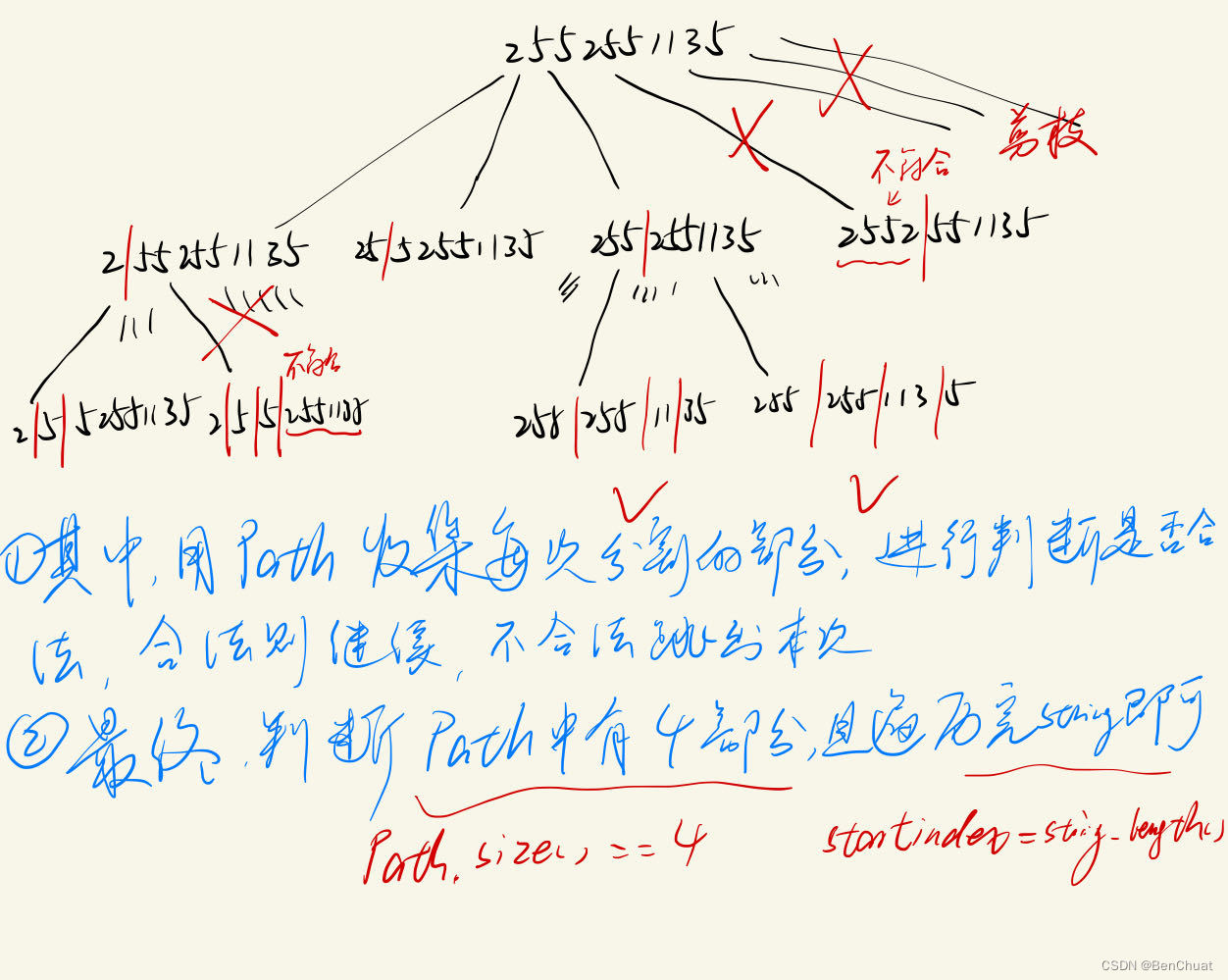
java复原IP 地址(力扣Leetcode93)
复原IP 地址 力扣原题链接 问题描述 有效 IP 地址正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2.201” 和 “192.168.1.1” 是有效 IP 地址,…...

k8s的创建资源的流程图
背景 在k8s中创建资源需要经过几个流程的协作,包括认证模块,授权模块和资源管理模块的共同处理的结果 k8s的创建资源的流程图 第一步认证模块: k8s需要确保操作的客户端是合法的用户,并且不是仿冒的,也就是判断这个u…...
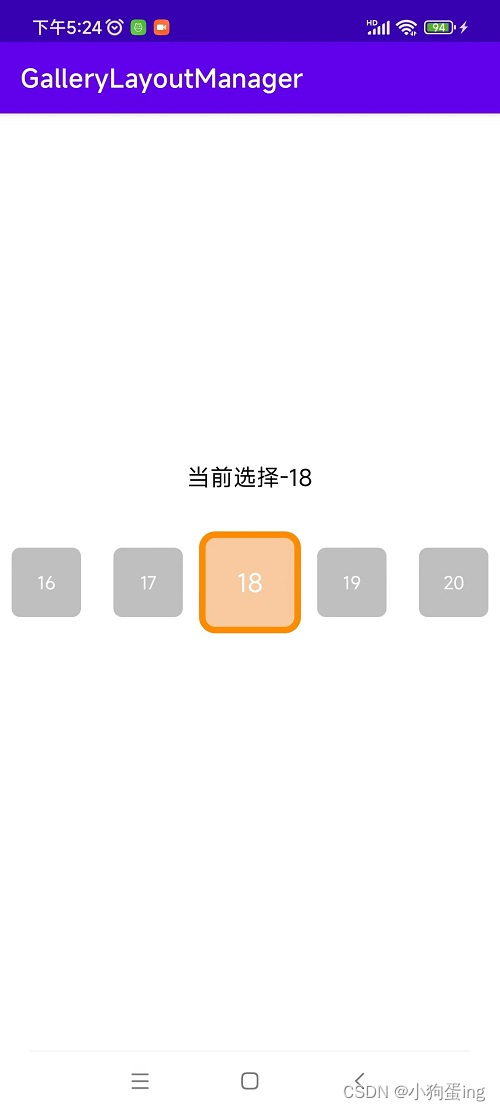
Android RecyclerView 滑动后选中的条目居中显示
话不多说先看效果: 实录效果视频如下 滚动居中 RecyclerView 在原有的RecyclerView 基础上操作,其他步骤不变,只是替换一下 manager 步骤 导入依赖 maven { url https://www.jitpack.io }//无限滚动implementation com.github.ZhaoChanghu:GalleryLayou…...
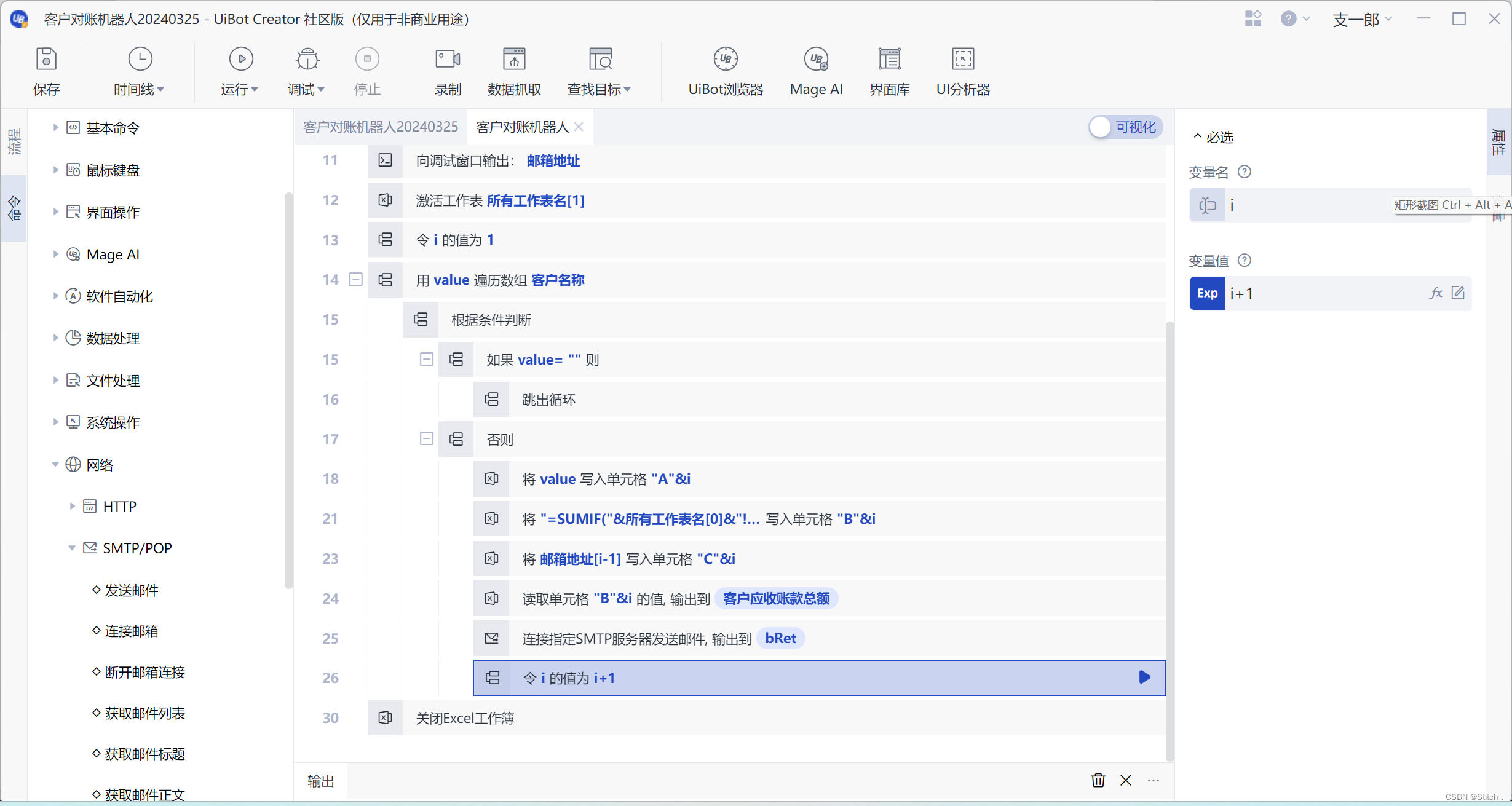
RPA-财务对账邮件应用自动化(客户对账机器人)
《财务对账邮件应用自动化》,将会使用邮箱的SMTP服务,小北把资源包绑定在这篇博客了 Uibot (RPA设计软件)———机器人的小项目友友们可以参考小北的课前材料五博客~ (本博客中会有部分课程ppt截屏,如有侵权请及请及时与小北我取得联系~) …...

Delphi模式编程
文章目录 Delphi模式编程涉及以下几个关键方面:**设计模式的应用****Delphi特性的利用****实际开发中的实践** Delphi模式编程的实例 Delphi模式编程是指在使用Delphi这一集成开发环境(IDE)和Object Pascal语言进行软件开发时,采用…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
