排序第五篇 归并排序
一 简介
归并排序(Merge Sort) 的基本思想是: 首先将待排序文件看成 n n n 个长度为1的有序子文件, 把这些子文件两两归并, 得到 n 2 \frac{n}{2} 2n 个长度为 2 的有序子文件;
然后再把这 n 2 \frac{n}{2} 2n 个有序的子文件两两归并, 如此反复,直到最后得到一个长度为 n n n 的有序文件为止, 这种排序方法称为二路归并排序。
在本文中,我们讨论的归并排序特指二路归并排序. 看一个示意图:

二 实现过程
归并排序的核心操作是将数组中前后相邻的两个有序序列归并为一个有序序列.
以java为例,看一个demo。
public class MergeSort {public static void main(String[] args) {Integer[] array = new Integer[]{30,45,10,30,50};System.out.println("归并排序初始顺序\n"+ Arrays.toString(array));mergeSort(array);System.out.println("归并排序最后顺序\n"+Arrays.toString(array));}static void mergeSort(Integer[] arr) {sort(arr, 0, arr.length - 1);}/**** 将两个有序序列归并为一个有序序列*/static void sort(Integer[] arr, int low, int high) {if (low >= high) {return;}int mid = low + (high - low) / 2;sort(arr, low, mid);sort(arr, mid + 1, high);merge(arr, low, mid, high);}static void merge(Integer[] arr, int low, int mid, int high) {//定义了一个临时数组int[] temp = new int[high - low + 1];int i = low, j = mid + 1, k = 0;while (i <= mid && j <= high) {temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];}while (i <= mid) {//将原数组从下标 low~middle 中剩余的复制到 temptemp[k++] = arr[i++];}while (j <= high) {//将原数组从下标 middle+1 ~ high 中剩余的复制到 temptemp[k++] = arr[j++];}for (i = 0; i < k; i++) {arr[low + i] = temp[i];}}
}
程序运行结果

归并排序算法
归并排序算法可看作递归算法, 虽然有的书写成不是递归算法同样实现了。
三 步骤
第一步: 一趟归并排序的基本思想是, 在某趟归并中, 设各子文件长度为len(最后一个子文件的长度可能会小于len), 则归并前 R [ 1.. n ] R[1..n] R[1..n] 共有 n l e n \frac{n}{len} lenn 个有序子文件。 调用归并操作对子文件进行归并时, 必须对子文件的个数可能是奇数、最后一个子文件和长度可能小于 l e n len len 这两种特殊情况进行处理:
- 若子文件个数为奇数,则最后个子文件无需和其他子文件归并;
- 若子文件个数为偶数,则要注意最后一对子文件中后一个子文件的区间上界为 n n n.
第二步: 归并排序的过程需要进行 l o g 2 log_{2} log2 n {n} n 趟。 每一趟排序的操作,就是将两个有序子文件进行归并,
而每一对有序子文件归并时,
记录的比较次数均小于等于记录的移动次数,
记录移动的次数均等于文件中记录的个数, 即每一趟归并的时间复杂度为 O ( n ) O(n) O(n)。
因此归并排序的时间复杂度为 O ( n l o g 2 O(nlog_{2} O(nlog2 n n n ) ) ).
从上述例子可以看出, 空间复杂度为 O ( n ) O(n) O(n)
归并排序是稳定的, 因为在每两个有序子文件 归并时, 若分别在两个有序子文件中出现有相同关键字的记录时, 归并排序算法能够使前一个子文件中同一关键字的记录被先复制,后一子文件中同一关键字的记录后被复制,从而确保它们的相对次序不变。
四 归并算法的优缺点
优点
- 适合于大规模数据量,并且要求稳定。
- 在基于比较的算法中是最高效率。
缺点
需要数据集长度的辅助空间, 在一定程度上增加了空间复杂度。
如果初始数据几乎填满整个内存,归并排序可能无法工作。
综上,归并算法是应用于大规模数据集最好的排序算法。
相关文章:

排序第五篇 归并排序
一 简介 归并排序(Merge Sort) 的基本思想是: 首先将待排序文件看成 n n n 个长度为1的有序子文件, 把这些子文件两两归并, 得到 n 2 \frac{n}{2} 2n 个长度为 2 的有序子文件; 然后再把这 n 2 \frac{n}{2} 2n 个有序的子…...
【Win】使用PowerShell和Webhooks轻松发送消息至Microsoft Teams
Microsoft Teams是一款由微软开发的团队协作和通讯工具。如果您对这个名字还不太熟悉,那么现在就是一个了解它的好时机。微软将Teams定位为其之前Skype for Business解决方案的继任者,并且它也提供了与其他基于频道的通讯应用程序(例如Slack、…...

ESCTF-OSINT赛题WP
这你做不出来?check ESCTF{湖北大学_嘉会园食堂} 这个识图可以发现是 淡水渔人码头 但是 osint 你要发现所有信息 聊天记录说国外 同时 提示给了美国 你综合搜索 美国 渔人码头 在美国旧金山的渔人码头(英语:Fisherman’s Wharf)是一个著名旅…...

2024蓝桥杯省赛保奖突击班-Day2-前缀和、差分、尺取_笔记_练习题解
3月25日-课堂笔记 前缀和预处理 O ( n ) \mathcal{O}(n) O(n) s[1] a[1]; for(int i 2; i < n; i)s[i] s[i - 1] a[i];利用前缀和查询区间和 O ( 1 ) O(1) O(1) long long calc(int l, int r) {return l 1 ? s[r] : s[r] - s[l - 1]; }差分序列的求法 c[1] a[…...

C++基础之虚函数(十七)
一.什么是多态 多态是在有继承关系的类中,调用同一个指令(函数),不同对象会有不同行为。 二.什么是虚函数 概念:首先虚函数是存在于类的成员函数中,通过virtual关键字修饰的成员函数叫虚函数。 性质&am…...

快速入门Kotlin①基本语法
前言 23年底读了一遍“Kotlin官方文档”,官方文档大而全,阅读下来,大有裨益。 此系列文章的目的是记录学习进程,同时,若能让读者迅速掌握重点内容并快速上手,那就再好不过了。 函数 带有两个 Int 参数、…...

【理解指针(四)】
文章目录 一、指针数组二、指针数组来模拟二维数组三、字符指针变量注意: 字符串的例子(曾经的一道笔试题) 四、数组指针变量1、什么是数组指针变量2、数组指针怎么初始化 五、二维数组传参的本质六、函数指针1、什么是函数指针变量2、函数的…...
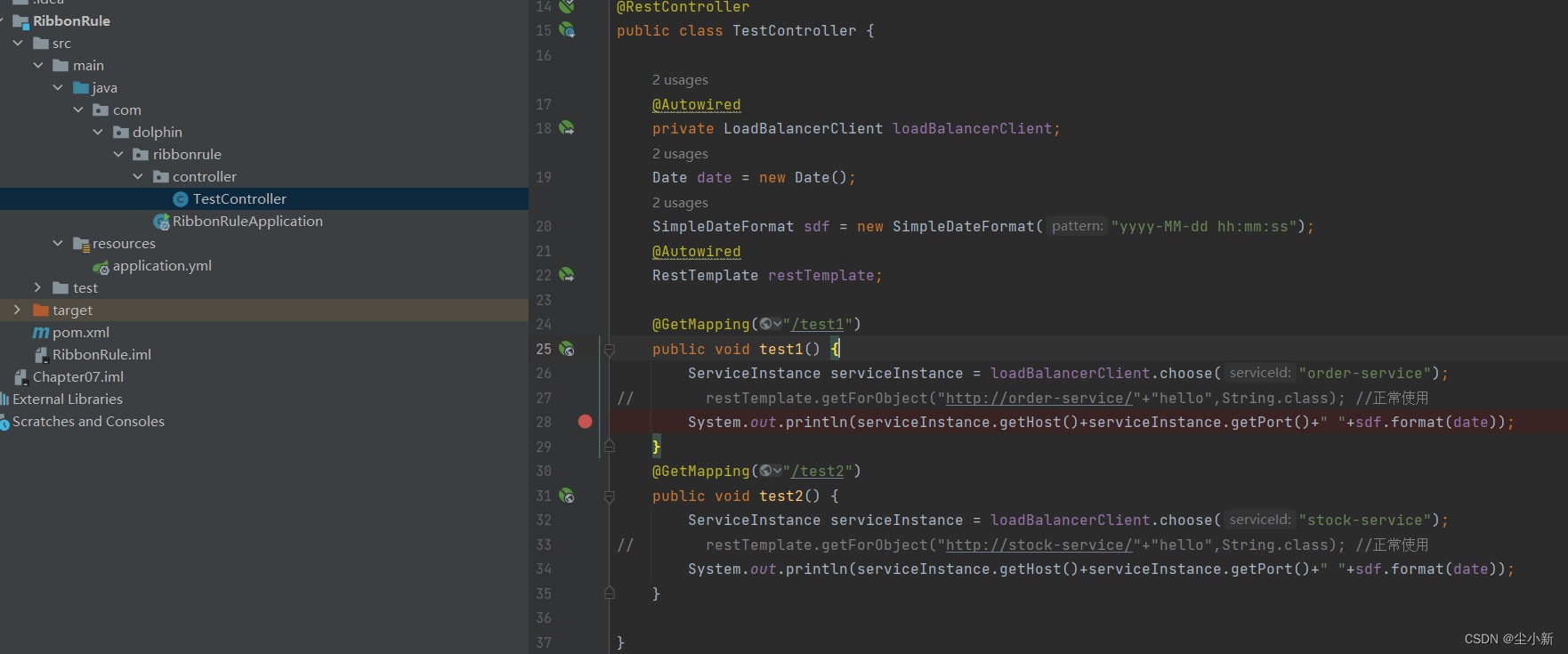
Ribbon简介
目录 一 、概念介绍 1、Ribbon是什么 2、认识负载均衡 2.1 服务器端的负载均衡 2.2 客户端的负载均衡 3、Ribbon工作原理 4、Ribbon的主要组件 IClientConfig ServerList ServerListFilter IRule Iping ILoadBalancer ServerListUpdater 5、Ribbon支持…...

【感悟《剑指offer》典型编程题的极练之路】02字符串篇!
个人主页:秋风起,再归来~ 文章所属专栏:《剑指offer》典型编程题的极练之路 个人格言:悟已往之不谏,知来者犹可追 克心守己,…...

通过 Docker 实现国产数据库 OpenGauss 开发环境搭建
通过 Docker 实现国产数据库 OpenGauss 开发环境搭建 一 前置准备 2.1 下载镜像 docker pull enmotech/opengauss:5.0.1构建镜像的 Dockerfile,方便后期实现个性化定制: FROM ubuntu:22.04 as builderARG TARGETARCHWORKDIR /warehouseRUN set -eux;…...
【Java】LinkedList模拟实现
目录 整体框架IMyLinkedList接口IndexNotLegalException异常类MyLinkedList类成员变量(节点信息)addFirst(头插)addLast(尾插)在指定位置插入数据判断是否存在移除第一个相等的节点移除所有相等的节点链表的长度打印链表释放回收链表 整体框架 IMyLinkedList接口 这个接口用来…...

ubuntu下mysql常用命令
1. 登录数据库 mysql -u root -p 2.创建数据库 create database 数据库名字 mysql> create database yourdb; Query OK, 1 row affected (0.03 sec)3.显示数据库 show databases; 实操结果如下 mysql> show databases; -------------------- | Database | ---…...
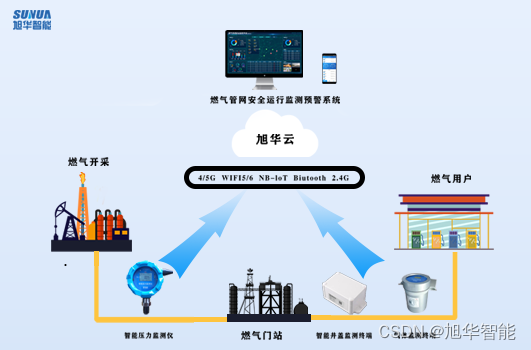
燃气官网安全运行监测系统-阀井燃气监测仪-旭华智能
近年来,燃气爆炸事故频发,造成了重大人员伤亡和财产损失。这也再次为我们敲响警钟,燃气是我们日常生活中不可或缺的能源,但其潜在的危险性也是不容小觑。因此在重要节点加装燃气阀井气体监测仪,并将数据上传到系统平台…...
)
vue 文件预览(docx、.xlsx、pdf)
1.ifream <iframe src"" ></iframe> 注: src里面是文件地址 2.vue-office 支持vue2和vue3提供docx、.xlsx、pdf多种文档的在线预览方案 2.1安装 #docx文档预览组件 npm install vue-office/docx vue-demi#excel文档预览组件 npm install vue-office…...
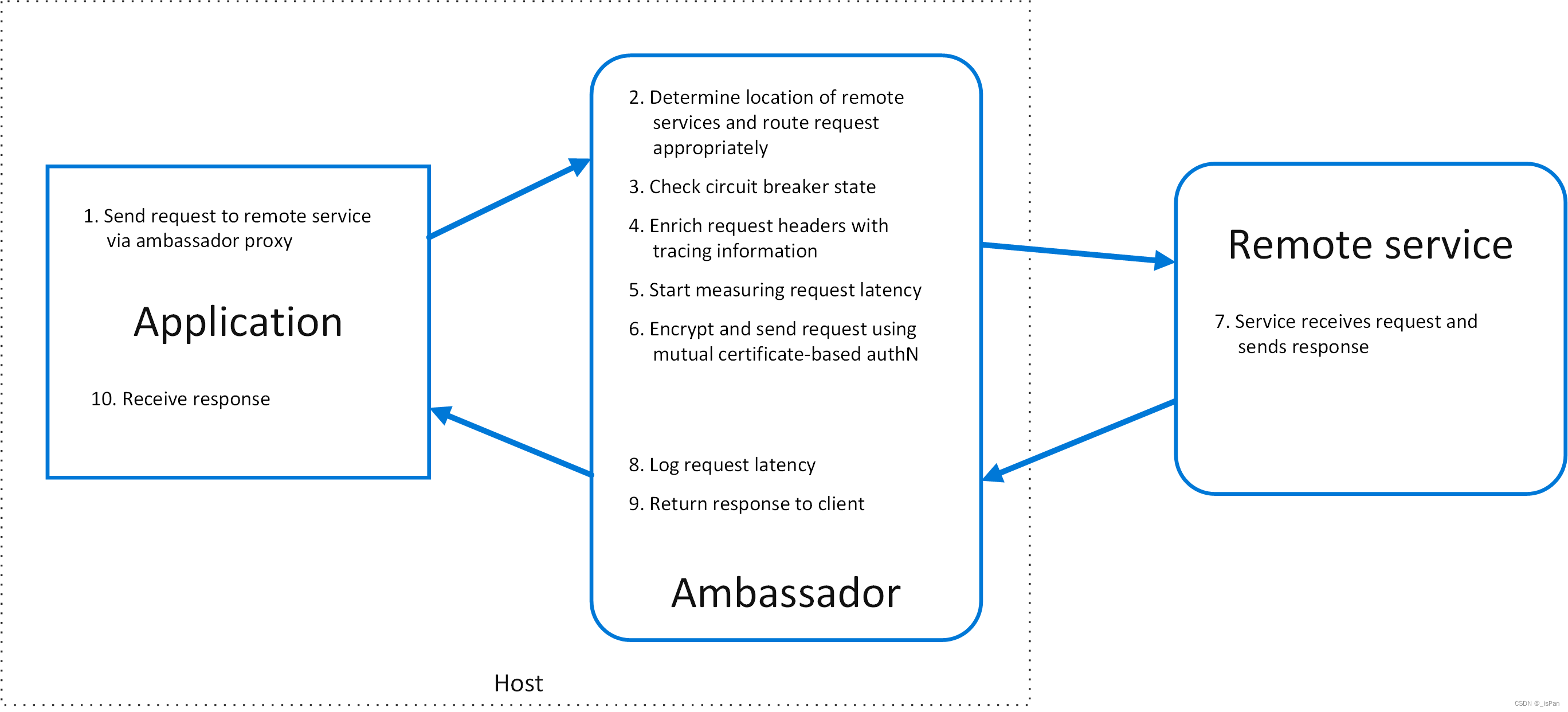
云架构(二) 大使模式
Ambassador pattern (https://learn.microsoft.com/en-us/azure/architecture/patterns/ambassador) 简单描述 创建一个助手服务,这个服务代表消费服务或者应用程序发送网络请求。大使服务可以看做是与客户机同一个位置的进程外代理。 这种…...

.NET Path类库的特殊方法
在.NET中Path类库是非常常用的一个类库,包含很多我们常用的方法,常用的方法这里就不详细说明了,这里记录下几个非常规的方法。 获取随机文件名: //将返回随机的文件名Console.WriteLine(Path.GetRandomFileName()); 获取禁止在路…...

【JVM】JVM常用性能调优参数详细介绍
JVM常用性能调优参数详细介绍 一、何时进行JVM调优二、性能调优三、JVM调优的基本原则四、JVM调优目标五、JVM调优的步骤六、JVM参数七、JVM参数解析及调优八、JVM参数使用手册8.1 内存相关8.2 GC策略相关8.3 GC日志相关8.4 异常相关8.5 问题定位及优化相关九、参考文档一、何时…...

React中的受控组件与非受控组件
受控组件与非受控组件 受控组件 组件(input, select)的状态与state的值绑定,组件的状态全程响应外部数据 class TestComponent extends React.Component {constructor (props) {super(props);this.state { username: lindaidai };}render () {return <input …...

uniapp实现u-datetime-picker时间选择器的默认日期定位,解决default-value不生效问题
uniapp实现u-datetime-picker,设置默认定位日期,解决default-value不生效问题 想实现的效果是点开时间选择器默认显示当前日期,而不是该选择器最早的日期 给选择器添加ref属性,如下: <u-datetime-picker :show&q…...

react native 使用ScrollView实现下拉更新,上拉加载更多
在React Native中,要实现下拉更新和上拉加载更多的功能,你需要自定义ScrollView组件,监听滚动事件并根据滚动的位置来判断何时触发更新和加载更多的操作。以下是一个基本的实现思路: 监听滚动事件:使用ScrollView的on…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
