鸿蒙OS开发实例:【ArkTS类库多线程I/O密集型任务开发】
使用异步并发可以解决单次I/O任务阻塞的问题,但是如果遇到I/O密集型任务,同样会阻塞线程中其它任务的执行,这时需要使用多线程并发能力来进行解决。
I/O密集型任务的性能重点通常不在于CPU的处理能力,而在于I/O操作的速度和效率。这种任务通常需要频繁地进行磁盘读写、网络通信等操作。此处以频繁读写系统文件来模拟I/O密集型并发任务的处理。
定义并发函数,内部密集调用I/O能力。
import fs from '@ohos.file.fs';// 定义并发函数,内部密集调用I/O能力
@Concurrent
async function concurrentTest(fileList: string[]) {// 写入文件的实现async function write(data, filePath) {let file = await fs.open(filePath, fs.OpenMode.READ_WRITE);await fs.write(file.fd, data);fs.close(file);}// 循环写文件操作for (let i = 0; i < fileList.length; i++) {write('Hello World!', fileList[i]).then(() => {console.info(`Succeeded in writing the file. FileList: ${fileList[i]}`);}).catch((err) => {console.error(`Failed to write the file. Code is ${err.code}, message is ${err.message}`)return false;})}return true;
}开始前熟悉鸿蒙文档
| 鸿蒙OS开发 | 更多内容↓点击 | HarmonyOS与OpenHarmony技术 |
|---|---|---|
| 鸿蒙技术文档 | 《鸿蒙NEXT星河版开发学习文档》 |
使用TaskPool执行包含密集I/O的并发函数:通过调用execute()方法执行任务,并在回调中进行调度结果处理。示例中的filePath1和filePath2的获取方式请参见获取应用文件路径。
import taskpool from '@ohos.taskpool';let filePath1 = ...; // 应用文件路径
let filePath2 = ...;// 使用TaskPool执行包含密集I/O的并发函数
// 数组较大时,I/O密集型任务任务分发也会抢占主线程,需要使用多线程能力
taskpool.execute(concurrentTest, [filePath1, filePath2]).then((ret) => {// 调度结果处理console.info(`The result: ${ret}`);
})本文参考引用HarmonyOS官方开发文档,基于API9。
鸿蒙Next核心技术分享
1、鸿蒙基础知识←《鸿蒙NEXT星河版开发学习文档》

2、鸿蒙ArkUI←《鸿蒙NEXT星河版开发学习文档》
3、鸿蒙进阶技术←《鸿蒙NEXT星河版开发学习文档》
4、鸿蒙就业高级技能←《鸿蒙NEXT星河版开发学习文档》

5、鸿蒙多媒体技术←《鸿蒙NEXT星河版开发学习文档》

6、鸿蒙南向驱动开发←《鸿蒙NEXT星河版开发学习文档》

7、鸿蒙南向内核设备开发←《鸿蒙NEXT星河版开发学习文档》

8、鸿蒙系统裁剪与移植←《鸿蒙NEXT星河版开发学习文档》

相关文章:

鸿蒙OS开发实例:【ArkTS类库多线程I/O密集型任务开发】
使用异步并发可以解决单次I/O任务阻塞的问题,但是如果遇到I/O密集型任务,同样会阻塞线程中其它任务的执行,这时需要使用多线程并发能力来进行解决。 I/O密集型任务的性能重点通常不在于CPU的处理能力,而在于I/O操作的速度和效率。…...
OpenStack部署
目录 一、安装环境 1.无网络使用该命令 2.修改主机名 3.配置hosts解析 4.配置本机免密 5.关闭防火墙和SElinux策略 6.关闭NewworkManager 7.修改yum源 7.1下载阿里源 7.2清空并加载缓存yum源 8.安装基本工具 9.系统升级 10.安装OPenStack的yum仓库 11.修改OPenSt…...
Java中的多线程和线程安全问题
线程 线程是操作系统进行调度的最小单位。一个进程至少包含一个主线程,而一个线程可以启动多个子线程。线程之间共享进程的资源,但也有自己的局部变量。多线程程序和普通程序的区别:每个线程都是一个独立的执行流;多个线程之间是…...
java Web会议信息管理系统 用eclipse定制开发mysql数据库BS模式java编程jdbc
一、源码特点 jsp 会议信息管理系统是一套完善的web设计系统,对理解JSP java SERLVET mvc编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,eclipse开发,数据库为Mysql5.0&am…...

lock4j学习记录
一种简单的,支持不同方案的高性能分布式锁 简介 lock4j是一个分布式锁组件,其提供了多种不同的支持以满足不同性能和环境的需求。 立志打造一个简单但富有内涵的分布式锁组件。 特性 简单易用,功能强大,扩展性强。支持redis…...
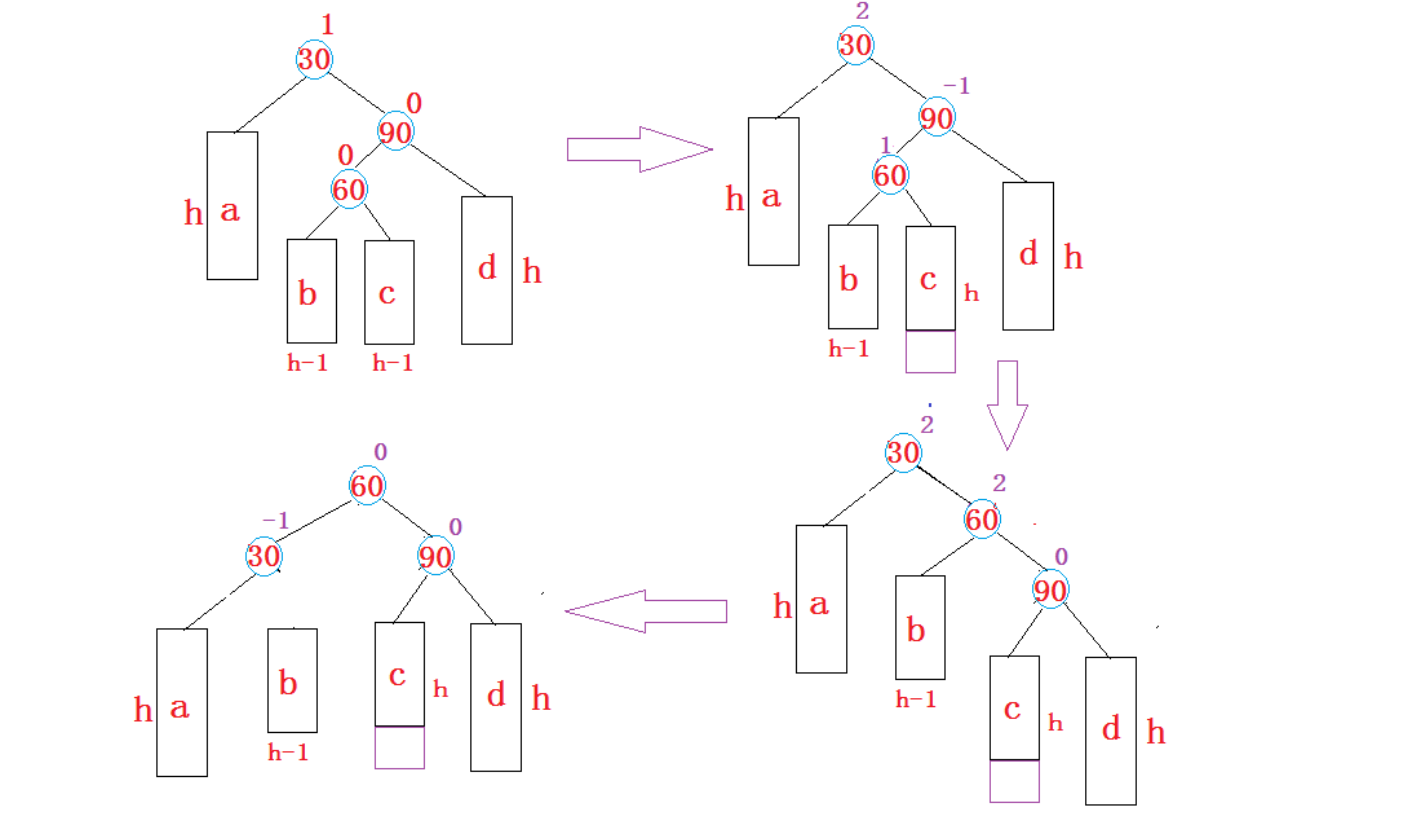
【C++庖丁解牛】自平衡二叉搜索树--AVL树
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 前言1 AVL树的概念2. AVL…...

ES5和ES6的深拷贝问题
深拷贝我们知道是引用值的一个问题,因为在拷贝的时候,拷贝的是在内存中同一个引用。所以当其中的一个应用值发生改变的时候,其他的同一个引用值也会发生变化。那么针对于这种情况,我们需要进行深度拷贝,这样就可以做到…...

阿里云发送短信配置
依赖 <dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpclient</artifactId><version>4.2.1</version> </dependency> <dependency><groupId>org.apache.httpcomponents</groupId&g…...

axios封装,请求取消和重试,请求头公共参数传递
axios本身功能已经很强大了,封装也无需过度,只要能满足自己项目的需求即可。 常规axios封装,只需要设置: 实现请求拦截实现响应拦截常见错误信息处理请求头设置 import axios from axios;// 创建axios实例 const service axios…...

隐私计算实训营学习五:隐语PSI介绍及开发指南
文章目录 一、SPU 实现的PSI介绍1.1 PSI定义和种类1.1.1 PSI定义和种类1.1.2 隐语PSI功能分层 1.2 SPU 实现的PSI介绍1.2.1 半诚实模型1.2.2 PSI实现位置 二、SPU PSI调度架构三、Secretflow PSI开发指南四、隐语PSI后续计划 一、SPU 实现的PSI介绍 1.1 PSI定义和种类 1.1.1 …...
ES的RestClient相关操作
ES的RestClient相关操作 Elasticsearch使用Java操作。 本文仅介绍CURD索引库和文档!!! Elasticsearch基础:https://blog.csdn.net/weixin_46533577/article/details/137207222 Elasticsearch Clients官网:https://ww…...

linux通用命令 ssh命令连接慢问题排查
系列文章目录 文章目录 系列文章目录一、 ssh 连接慢3.1 查找原因3.2 解决方案 一、 ssh 连接慢 最近的 koji 服务器 使用 ssh 连接很慢。 3.1 查找原因 可以通过 ssh -vvv 192.168.0.123 或 time ssh root192.168.0.123 exit 查找原因如下: SERVER的SSHD会去DN…...
7.卷积神经网络与计算机视觉
计算机视觉是一门研究如何使计算机识别图片的学科,也是深度学习的主要应用领域之一。 在众多深度模型中,卷积神经网络“独领风骚”,已经被称为计算机视觉的主要研究根据之一。 一、卷积神经网络的基本思想 卷积神经网络最初由 Yann LeCun&a…...

Linux|如何管理多个Git身份
摘要 关于如何管理不同项目和多个Git身份。 作为一名通用软件开发者,我经常发现自己在处理各种各样的项目,每个项目都有自己的要求和期望。这包括为个人、工作和客户项目管理不同的Git身份。以下是我组织Git仓库以简化这一过程的方法。 目录组织 我将我的…...

力扣---最长回文子串---二维动态规划
二维动态规划思路: 首先,刚做完这道题:力扣---最长有效括号---动态规划,栈-CSDN博客,所以会有一种冲动,设立g[i],表示以第i位为结尾的最长回文子串长度,然后再遍历一遍取最大长度即可…...
(一)kafka实战——kafka源码编译启动
前言 本节内容是关于kafka消息中间键的源码编译,并通过idea工具实现kafka服务器的启动,使用的kafka源码版本是3.6.1,由于kafka源码是通过gradle编译的,以及服务器是通过scala语言实现,我们要预先安装好gradle编译工具…...

Spring Boot 使用 Redis
1,Spring 是如何集成Redis的? 首先我们要使用jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency><dependency><gro…...

火车头通过关键词采集文章的原理
随着互联网信息的爆炸式增长,网站管理员和内容创作者需要不断更新和发布新的文章,以吸引更多的用户和提升网站的排名。而火车头作为一款智能文章采集工具,在这一过程中发挥着重要作用。本文将探讨火车头如何通过关键词采集文章,以…...

Kafka 面试题及参考答案
目录 1. Kafka 的核心特性是什么? 2. Kafka 为什么能够实现高吞吐量? 3. Kafka 的消息丢失是...

【Qt 学习笔记】Day1 | Qt 背景介绍
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Day1 | Qt 背景介绍 文章编号:Qt 学习笔记 / 01 文章目录…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...


