【力扣】45.跳跃游戏Ⅱ
45.跳跃游戏Ⅱ
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
- 0 <= j <= nums[i]
- i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
- 1 <= nums.length <= 104
- 0 <= nums[i] <= 1000
- 题目保证可以到达
nums[n-1]
解题方案
- C 贪心算法
#define MAX(a, b) ((a) > (b) ? (a) : (b))int jump(int* nums, int numsSize) {int max_tg = 0; // 能跳跃到的最远位置int step = 0; // 跳跃次数int next_start = 0; // 下次起跳点for (int i = 0; i < numsSize - 1; i++) {max_tg = MAX(max_tg, i + nums[i]);if (i == next_start) {next_start = max_tg; // 更新起跳位置step++; // 跳跃计数}}return step;
}
复杂度分析
时间复杂度为 O(n),其中 nnn 是数组长度。
空间复杂度为 O(1)。
相关文章:

【力扣】45.跳跃游戏Ⅱ
45.跳跃游戏Ⅱ 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i]i j < n 返回到达 n…...

containerd使用了解
containerd使用了解 yum安装 [rootvm ~]# curl -o /etc/yum.repos.d/docker.repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo [rootvm ~]# yum list | grep containerd containerd.io.x86_64 1.6.28-3.1.el7 doc…...

gateway 分发时若两个服务的路由地址一样,怎么指定访问想要的服务下的地址
1.思路 在使用Spring Cloud Gateway时,如果两个服务的路由地址相同,可以通过Predicate(断言)和Filter(过滤器)的组合来实现根据请求的不同条件将请求分发到不同的服务下的地址。 使用Predicate进行路由条件…...

【LeetCode】三月题解
文章目录 [2369. 检查数组是否存在有效划分](https://leetcode.cn/problems/check-if-there-is-a-valid-partition-for-the-array/)思路:代码: [1976. 到达目的地的方案数](https://leetcode.cn/problems/number-of-ways-to-arrive-at-destination/) 思路…...

云手机:实现便携与安全的双赢
随着5G时代的到来,云手机在各大游戏、直播和新媒体营销中扮演越来越重要的角色。它不仅节约了成本,提高了效率,而且在边缘计算和云技术逐渐成熟的背景下,展现出了更大的发展机遇。 云手机的便携性如何? 云手机的便携性…...
fast_bev学习笔记
目录 一. 简述二. 输入输出三. github资源四. 复现推理过程4.1 cuda tensorrt 版 一. 简述 原文:Fast-BEV: A Fast and Strong Bird’s-Eye View Perception Baseline FAST BEV是一种高性能、快速推理和部署友好的解决方案,专为自动驾驶车载芯片设计。该框架主要包…...
Collection与数据结构链表与LinkedList(三):链表精选OJ例题(下)
1. 分割链表 OJ链接 class Solution {public ListNode partition(ListNode head, int x) {if(head null){return null;//空链表的情况}ListNode cur head;ListNode formerhead null;ListNode formerend null;ListNode latterhead null;ListNode latterend null;//定义…...
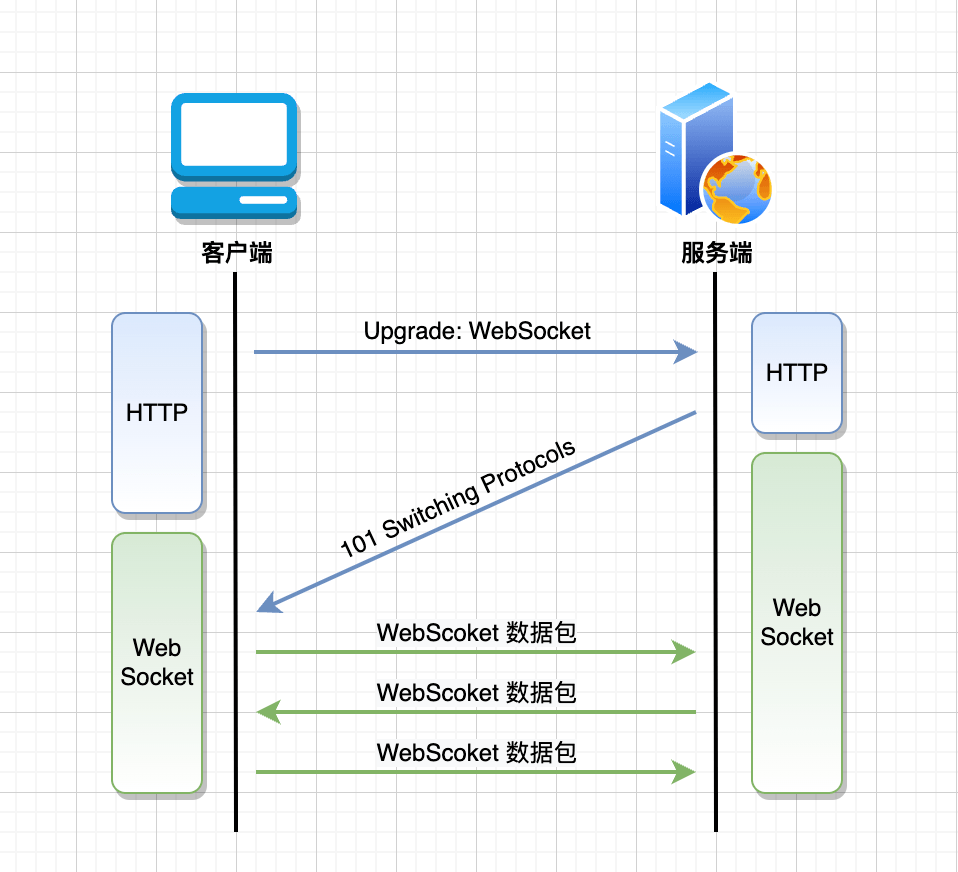
05 | Swoole 源码分析之 WebSocket 模块
首发原文链接:Swoole 源码分析之 WebSocket 模块 大家好,我是码农先森。 引言 WebSocket 是一种在单个 TCP 连接上进行全双工通信的协议。它允许客户端和服务器之间进行实时数据传输。 与传统的 HTTP 请求-响应模型不同,WebSocket 可以保持…...

Vue--------父子/兄弟组件传值
父子组件 子组件通过 props 属性来接受父组件的数据,然后父组件在子组件上注册监听事件,子组件通过 emit 触发事件来向父组件发送数据。 defineProps接收 let props defineProps({data: Array, }); defineModel接收 let bb defineModel("sit…...

Qt实现Kermit协议(一)
1 概述 Kermit文件运输协议提供了一条从大型计算机下载文件到微机的途径。它已被用于进行公用数据传输。 其特性如下: Kermit文件运输协议是一个半双工的通信协议。它支持7位ASCII字符。数据以可多达96字节长度的可变长度的分组形式传输。对每个被传送分组需要一个确认。Kerm…...
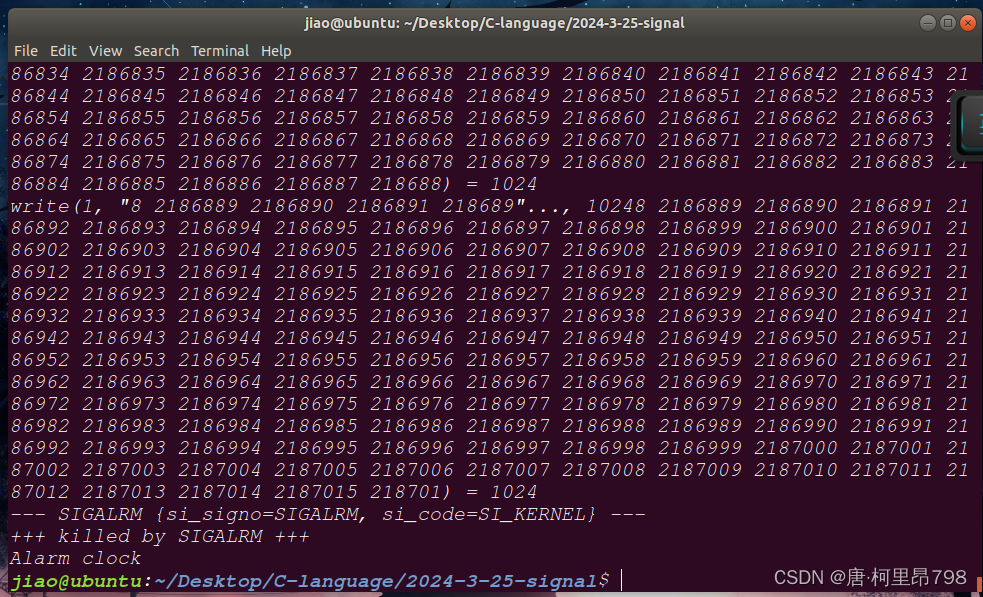
linux在使用重定向写入文件时(使用标准C库函数时)使处理信号异常(延时)--问题分析
linux在使用重定向写入文件时(使用标准C库函数时)使处理信号异常(延时)–问题分析 在使用alarm函数进行序号处理测试的时候发现如果把输出重定向到文件里面会导致信号的处理出现严重的延迟(ubuntu18) #include <stdio.h> #include <stdlib.h> #include <unist…...
淘宝扭蛋机小程序:趣味购物新体验,惊喜连连等你来
在数字化时代,淘宝始终站在创新的前沿,不断探索和引领电商行业的发展趋势。今天,我们欣然宣布,经过精心研发和打磨,淘宝扭蛋机小程序正式上线,为用户带来一场充满趣味与惊喜的购物新体验。 淘宝扭蛋机小程…...

linux:生产者消费者模型
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《Linux》 文章目录 前言一、生产者消费者模型二、基于阻塞队列的生产者消费者模型代码实现 总结 前言 本文是对于生产者消费者模型的知识总结 一、生产者消费者模型 生产者消费者模型就是…...

C++教学——从入门到精通 5.单精度实数float
众所周知,三角形的面积公式是(底*高)/2 那就来做个三角形面积计算器吧 到吗如下 #include"bits/stdc.h" using namespace std; int main(){int a,b;cin>>a>>b;cout<<(a*b)/2; } 这不对呀,明明是7.5而他却是7,…...

面向对象设计之单一职责原则
设计模式专栏:http://t.csdnimg.cn/6sBRl 目录 1.单一职责原则的定义和解读 2.如何判断类的职责是否单一 3.类的职责是否越细化越好 4.总结 1.单一职责原则的定义和解读 单一职责原则(Single Responsibility Principle,SRP)的描述:一个类…...

蓝桥杯真题:单词分析
import java.util.Scanner; //1:无需package //2: 类名必须Main, 不可修改 public class Main{public static void main(String[]args) {Scanner sannernew Scanner(System.in);String strsanner.nextLine();int []anew int [26];for(int i0;i<str.length();i) {a[str.charA…...

Python字符串字母大小写变换,高级Python开发技术
寻找有志同道合的小伙伴,互帮互助,群里还有不错的视频学习教程和PDF电子书! ‘’’ demo ‘tHis iS a GOod boOK.’ print(demo.casefold()) print(demo.lower()) print(demo.upper()) print(demo.capitalize()) print(demo.title()) print(dem…...

CentOS常用功能命令集合
1、删除指定目录下所有的空目录 find /xxx -type d -empty -exec rmdir {} 2、删除指定目录下近7天之前的日志文件 find /xxx -name "*.log" -type f -mtime 7 -exec rm -f {} \; 3、查询指定目录下所有的指定格式文件(比如PDF文件) find…...

黑马点评项目笔记 II
基于Stream的消息队列 stream是一种数据类型,可以实现一个功能非常完善的消息队列 key:队列名称 nomkstream:如果队列不存在是否自动创建,默认创建 maxlen/minid:设置消息队列的最大消息数量 *|ID 唯一id:…...

关于一篇知乎答案的重现
〇、前言 早上在逛知乎的时候,瞥见了一篇答案:如何通俗解释Docker是什么?感觉很不错,然后就耐着性子看了下,并重现了作者的整个过程。但是并不顺利,记载一下这些坑。嫌麻烦的话可以直接clone 研究…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
