Acwing: 一道关于线段树的好题(有助于全面理解线段树)
题目链接🔗:2643. 序列操作 - AcWing题库
前驱知识:需要理解线段树的结构和程序基本框架、以及懒标记的操作。
题目描述
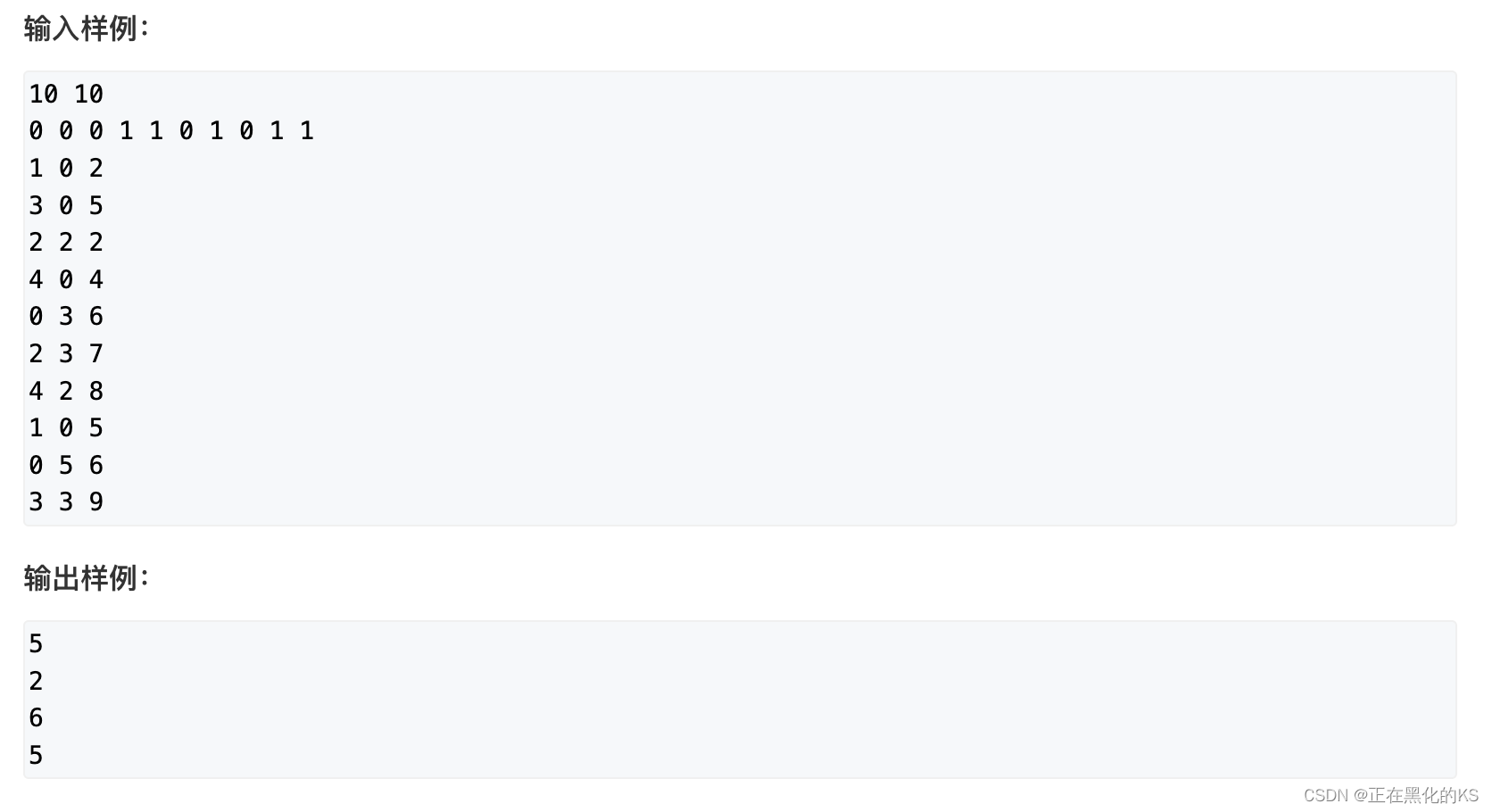
题目分析
对区间在线进行修改和查询,一般就是用线段树来解决,观察到题目一共有五个操作:
我们首先要思考需要用线段树维护哪些信息,通过维护这些信息,在查询时能够得到需要的答案。
根据查询的内容,我们发现需要维护区间内1的个数
,以及区间内最多连续1的个数
由于题目的操作对象就是0和1,我们可以想到对称维护0和1的信息(主要是因为存在操作2
那么综合来看,我们可以维护线段树的以下信息:
:区间左端点
:区间右端点
:区间内1的个数
:区间内0的个数
:区间内左边最多连续1的个数
:区间内左边最多连续0的个数
:区间内右边最多连续1的个数
:区间内右边最多连续0的个数
:区间内最长连续0的个数
:区间内最长连续1的个数
:操作0对应的懒标记
:操作1对应的懒标记
:操作2对应的懒标记
具体维护方案如下
AC代码
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std ;const int N = 1e5 + 10 ; int n, m, a[N] ;
struct Node
{int l, r ; int sum0, sum1, l0, l1, r0, r1, m0, m1 ; bool flag0, flag1, rev ;
}tr[4 * N] ; void pushup(int u)
{tr[u].sum0 = tr[u << 1].sum0 + tr[u << 1 | 1].sum0 ; tr[u].sum1 = tr[u << 1].sum1 + tr[u << 1 | 1].sum1 ;tr[u].l0 = (tr[u << 1].sum1) ? tr[u << 1].l0 : tr[u << 1].sum0 + tr[u << 1 | 1].l0 ;tr[u].l1 = (tr[u << 1].sum0) ? tr[u << 1].l1 : tr[u << 1].sum1 + tr[u << 1 | 1].l1 ;tr[u].r0 = (tr[u << 1 | 1].sum1) ? tr[u << 1 | 1].r0 : tr[u << 1 | 1].sum0 + tr[u << 1].r0 ; tr[u].r1 = (tr[u << 1 | 1].sum0) ? tr[u << 1 | 1].r1 : tr[u << 1 | 1].sum1 + tr[u << 1].r1 ;tr[u].m0 = max(max(tr[u << 1].m0, tr[u << 1 | 1].m0), tr[u << 1].r0 + tr[u << 1 | 1].l0) ;tr[u].m1 = max(max(tr[u << 1].m1, tr[u << 1 | 1].m1), tr[u << 1].r1 + tr[u << 1 | 1].l1) ;
}void pushup_Node(Node &root, Node ls, Node rs)
{root.sum0 = ls.sum0 + rs.sum0 ; root.sum1 = ls.sum1 + rs.sum1 ; root.l0 = (ls.sum1) ? ls.l0 : ls.sum0 + rs.l0 ; root.l1 = (ls.sum0) ? ls.l1 : ls.sum1 + rs.l1 ; root.r0 = (rs.sum1) ? rs.r0 : rs.sum0 + ls.r0 ; root.r1 = (rs.sum0) ? rs.r1 : rs.sum1 + ls.r1 ;root.m0 = max(max(ls.m0, rs.m0), ls.r0 + rs.l0) ; root.m1 = max(max(ls.m1, rs.m1), ls.r1 + rs.l1) ;
}void pushdown(int u)
{if (tr[u].flag0) {tr[u << 1].sum0 = tr[u << 1].l0 = tr[u << 1].r0 = tr[u << 1].m0 = tr[u << 1].r - tr[u << 1].l + 1 ; tr[u << 1 | 1].sum0 = tr[u << 1 | 1].l0 = tr[u << 1 | 1].r0 = tr[u << 1 | 1].m0 = tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1 ;tr[u << 1].sum1 = tr[u << 1].l1 = tr[u << 1].r1 = tr[u << 1].m1 = 0 ; tr[u << 1 | 1].sum1 = tr[u << 1 | 1].l1 = tr[u << 1 | 1].r1 = tr[u << 1 | 1].m1 = 0 ; tr[u << 1].flag0 = tr[u << 1 | 1].flag0 = true ; tr[u << 1].flag1 = tr[u << 1 | 1].flag1 = tr[u << 1].rev = tr[u << 1 | 1].rev = false ;tr[u].flag0 = false ; }if (tr[u].flag1) {tr[u << 1].sum1 = tr[u << 1].l1 = tr[u << 1].r1 = tr[u << 1].m1 = tr[u << 1].r - tr[u << 1].l + 1 ; tr[u << 1 | 1].sum1 = tr[u << 1 | 1].l1 = tr[u << 1 | 1].r1 = tr[u << 1 | 1].m1 = tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1 ;tr[u << 1].sum0 = tr[u << 1].l0 = tr[u << 1].r0 = tr[u << 1].m0 = 0 ;tr[u << 1 | 1].sum0 = tr[u << 1 | 1].l0 = tr[u << 1 | 1].r0 = tr[u << 1 | 1].m0 = 0 ;tr[u << 1].flag1 = tr[u << 1 | 1].flag1 = true ;tr[u << 1 | 1].flag0 = tr[u << 1 | 1].flag0 = tr[u << 1].rev = tr[u << 1 | 1].rev = false ;tr[u].flag1 = false ;}if (tr[u].rev) {swap(tr[u << 1].sum0, tr[u << 1].sum1) ;swap(tr[u << 1 | 1].sum0, tr[u << 1 | 1].sum1) ;swap(tr[u << 1].l0, tr[u << 1].l1) ; swap(tr[u << 1 | 1].l0, tr[u << 1 | 1].l1) ;swap(tr[u << 1].r0, tr[u << 1].r1) ; swap(tr[u << 1 | 1].r0, tr[u << 1 | 1].r1) ;swap(tr[u << 1].m0, tr[u << 1].m1) ; swap(tr[u << 1 | 1].m0, tr[u << 1 | 1].m1) ;tr[u << 1].rev ^= 1, tr[u << 1 | 1].rev ^= 1 ; tr[u].rev = 0 ;}
}void build(int u, int l, int r)
{tr[u].l = l, tr[u].r = r ; if (l == r) {tr[u].sum0 = tr[u].l0 = tr[u].r0 = tr[u].m0 = a[r] ^ 1 ; tr[u].sum1 = tr[u].l1 = tr[u].r1 = tr[u].m1 = a[r] & 1 ; return ; }int mid = l + r >> 1 ;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r) ; pushup(u) ;
}void change1(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) {tr[u].sum1 = tr[u].l1 = tr[u].r1 = tr[u].m1 = 0 ; tr[u].sum0 = tr[u].l0 = tr[u].r0 = tr[u].m0 = tr[u].r - tr[u].l + 1 ; tr[u].flag0 = true, tr[u].flag1 = tr[u].rev = false ;return ;}pushdown(u) ; int mid = tr[u].l + tr[u].r >> 1 ; if (l <= mid) change1(u << 1, l, r) ; if (r > mid) change1(u << 1 | 1, l, r) ; pushup(u) ;
}void change2(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) {tr[u].sum0 = tr[u].l0 = tr[u].r0 = tr[u].m0 = 0 ; tr[u].sum1 = tr[u].l1 = tr[u].r1 = tr[u].m1 = tr[u].r - tr[u].l + 1 ; tr[u].flag1 = true, tr[u].flag0 = tr[u].rev = false ;return ;}pushdown(u) ; int mid = tr[u].l + tr[u].r >> 1 ; if (l <= mid) change2(u << 1, l, r) ; if (r > mid) change2(u << 1 | 1, l, r) ; pushup(u) ;
}void Reverse(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) {swap(tr[u].sum0, tr[u].sum1) ; swap(tr[u].l0, tr[u].l1) ; swap(tr[u].r0, tr[u].r1) ; swap(tr[u].m0, tr[u].m1) ; tr[u].rev ^= 1 ; return ; }pushdown(u) ; int mid = tr[u].l + tr[u].r >> 1 ; if (l <= mid) Reverse(u << 1, l, r) ; if (r > mid) Reverse(u << 1 | 1, l, r) ;pushup(u) ;
}int ask1(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum1 ; pushdown(u) ; int mid = tr[u].l + tr[u].r >> 1 ; int sum = 0 ; if (l <= mid) sum = ask1(u << 1, l, r) ; if (r > mid) sum += ask1(u << 1 | 1, l, r) ; return sum ;
}Node ask2(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r) return tr[u] ; pushdown(u) ; int mid = tr[u].l + tr[u].r >> 1 ; Node res ; if (l > mid) return ask2(u << 1 | 1, l, r) ; if (r <= mid) return ask2(u << 1, l, r) ; Node ls = ask2(u << 1, l, r), rs = ask2(u << 1 | 1, l, r) ; pushup_Node(res, ls, rs) ; return res ;
}int main()
{ios::sync_with_stdio(false) ; cin >> n >> m ; for (int i = 1 ; i <= n ; i ++ ) cin >> a[i] ;build(1, 1, n) ; while (m -- ) {int opt, l, r ; cin >> opt >> l >> r ; l ++, r ++ ; if (opt == 0) change1(1, l, r) ; else if (opt == 1) change2(1, l, r) ; else if (opt == 2) Reverse(1, l, r) ; else if (opt == 3) cout << ask1(1, l , r) << endl ;else cout << ask2(1, l, r).m1 << endl ; }return 0 ;
}相关文章:

Acwing: 一道关于线段树的好题(有助于全面理解线段树)
题目链接🔗:2643. 序列操作 - AcWing题库 前驱知识:需要理解线段树的结构和程序基本框架、以及懒标记的操作。 题目描述 题目分析 对区间在线进行修改和查询,一般就是用线段树来解决,观察到题目一共有五个操作&…...

DD-1/40 10-40mA型【接地继电器】
系列型号: DD-1/40接地继电器 DD-1/50接地继电器 DD-1/60接地继电器 一、 用途及工作原理 DD-1型接地继电器为瞬时动作的过电流继电器,用作小电流接地电力系统高电压三相交流发电机和电动机的接地零序过电流保护。继电器线圈接零序电流互感器(电缆式、母…...

【女神节】简单使用C/C++和Python嵌套for循环生成一个小爱心
目录 前言实现分析代码实现代码如下效果如下优化效果代码如下效果如下总结尾叙前言 女神节马上到了,有女朋友的小伙伴是不是已经精心准好礼物了呢!对于已婚男士,是不是整愁今天又该送什么礼物呢!说真的,我也整愁着,有什么要推荐么,评论留言下! 实现分析 可以先在纸上或…...

Biome-BGC生态系统模型与Python融合技术实践应用
查看原文>>> Biome-BGC生态系统模型与Python融合技术实践应用 Biome-BGC是利用站点描述数据、气象数据和植被生理生态参数,模拟日尺度碳、水和氮通量的有效模型,其研究的空间尺度可以从点尺度扩展到陆地生态系统。 在Biome-BGC模型中…...

ESP32 GPIO使用
ESP32 GPIO使用 #define GPIO_OUT_PIN 2 //定义引脚号 #define GPIO_OUTPUT_PIN_SEL (1<<GPIO_OUT_PIN) //定义输出引脚的宏,用来将输出引脚号转换为位掩码void bsp_gpio_init(){gpio_config_t io_conf;io_conf.pin_bit_mask GPIO_OUTPUT_PIN_SE…...
JavaScript 高级4 :正则表达式
JavaScript 高级4 :正则表达式 Date: January 19, 2023 Text: 正则表达式、正则表达式特殊字符、正则表达式中的替换 目标: 能够说出正则表达式的作用 能够写出简单的正则表达式 能够使用正则表达式对表单进行验证 能够使用正则表达式替换内容 正则…...
如何让AI帮你干活-娱乐(3)
背景今天的话题会偏代码技巧一些,对于以前没有接触过代码的朋友或者接触代码开发经验较少的朋友会有些吃力。上篇文章介绍了如何广视角的生成相对稳定的视频。昨天的实现相对简单,主要用的是UI界面来做生成。但是生成的效果其实也显而易见,不…...
webview的工作、内存泄漏、漏洞以及缓存机制原理原理+方案解决
分析一段appium的日志来分析webview的工作原理,文章尾部附有自动化脚本及完整日志: 解析: 获取上下文列表 服务端发送命令adb shell cat /proc/net/unix获取域套接字列表。那什么是域套接字呢? 域套接字:是unix系统里…...
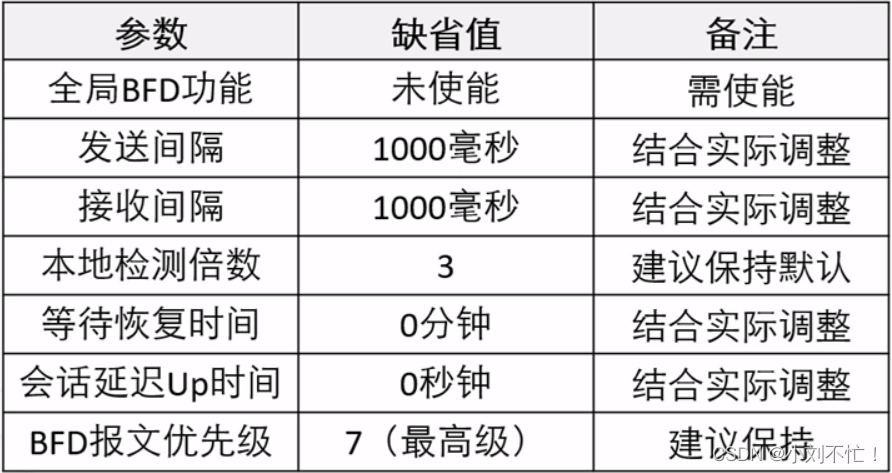
BFD协议原理
BFD协议原理引入背景不使用BFD带来的问题OSPF感知慢VRRP产生次优路径BFD技术简介BFD会话建立方式和检测机制BFD会话建立过程BFD工作流程BFD的单臂回声BFD默认参数以及调整方法总结引入背景 随着网络应用的广泛部署,网络发生中断可能影响业务正常运行并造成重大损失…...

你把骑行当什么? 它就是你需要的
1.骑行是一种有活力的运动,尝试一下你一定会喜欢上它的!2.把骑行当作一种娱乐,让自己快乐地体验自然的美!3.骑行可以帮助你改变心态,让你的心情变得更加愉悦!4.让骑行成为你每天的计划,看看骑行…...

python基础系列 —— 迭代器与内置高阶函数
目录 一、迭代器 1、基本概念 2、如何定义一个迭代器 3、如果判断对象是否是迭代器 4、如何重置迭代器 5、如何调用迭代器 二、高阶函数 1、map函数 2、filter函数 3、reduce函数 4、sorted函数 一、迭代器 1、基本概念 迭代:是一个重复的过程,每次重复…...
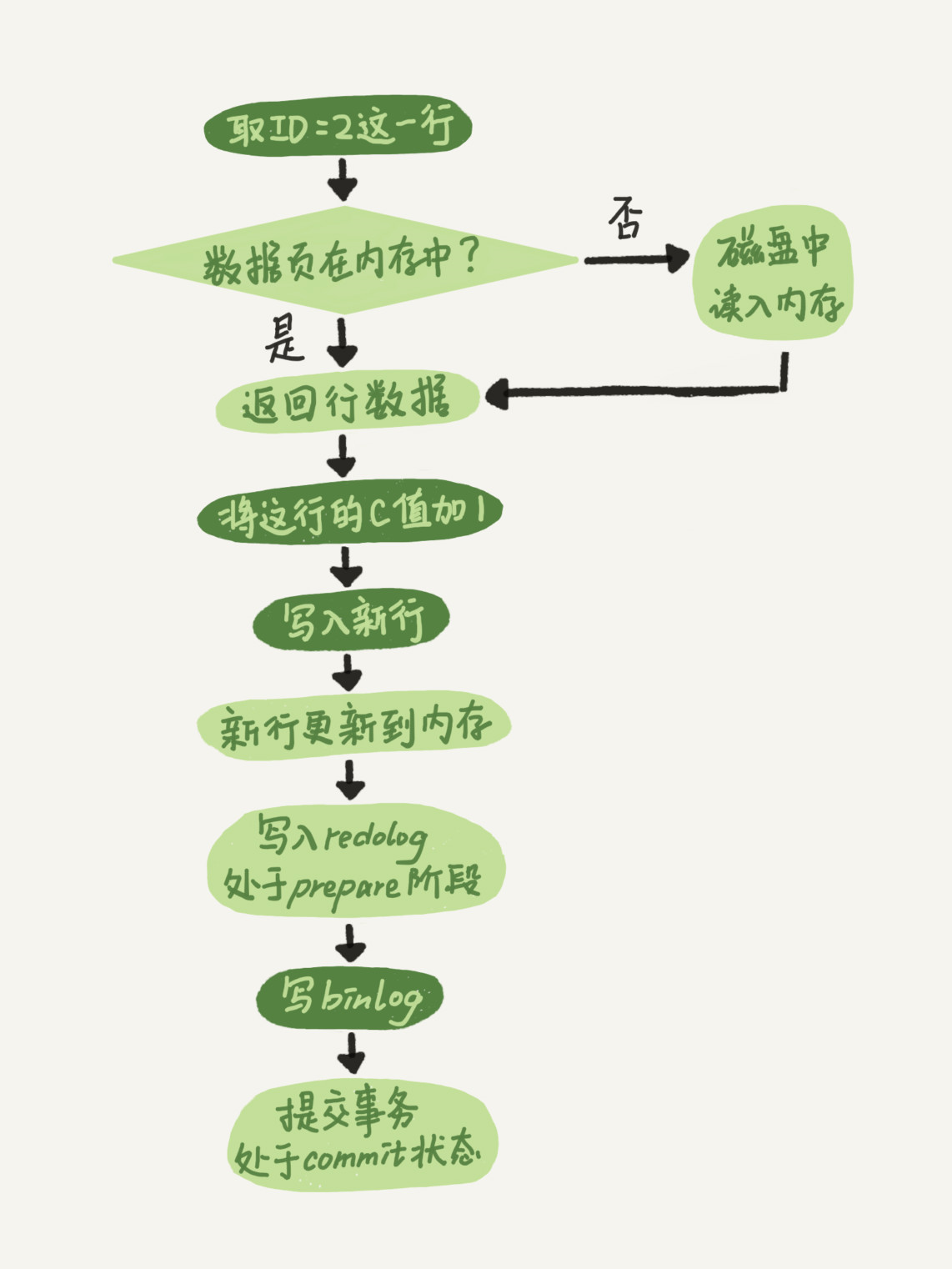
MySQL面试题-日志
目录 1.MySQL 中常见的日志有哪些? 2.慢查询日志有什么用? 3.binlog 主要记录了什么? 4.Mysql的binlog有几种录入格式?分别有什么区别? 5.redo log 如何保证事务的持久性? 6.页修改之后为什么不直接刷…...
Android 10.0 去掉Launcher3默认给 icon增加的APK图标白边
1.概述 在10.0的系统产品开发中,Launcher3定制化开发中,发现在给第三方app的icon绘制图标的时候,会有白边第三方app的图标没有完全绘制出来,而系统app不存在这个问题,是完全绘制出来的,所以需要分析图标绘制类来解决这个问题 2.去掉Launcher3默认给 icon增加的APK图标白…...
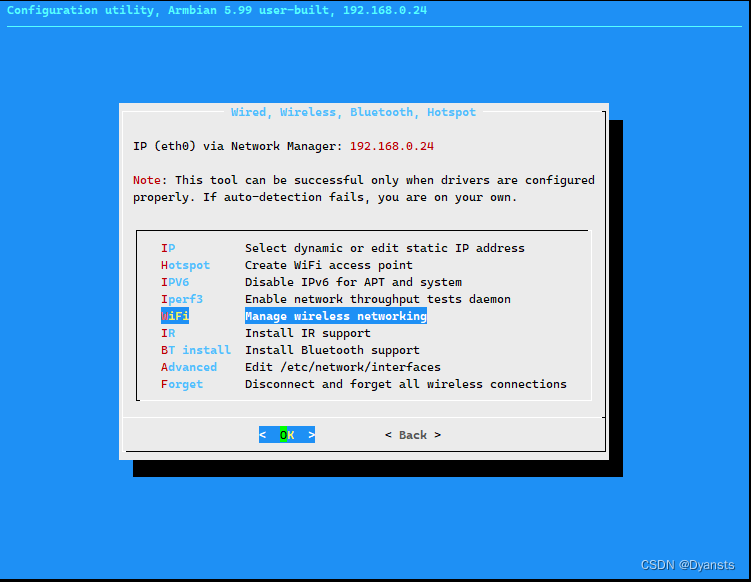
E900V21C(S905L-armbian)安装armbian-Ubuntu(WiFi)
基本上是s905L芯片的刷机都是如此,包括Q7等 在网上寻找好多的教程关于e900v21c的刷机包和教程都少的可怜,唯一的就是这个:山东联通版创维E900V21C盒子刷入Armbiam并安装宝塔和Docker,但他是不能用WiFi和蓝牙的然后就是寻找s90l的…...

tpc协议的3次握手和4次挥手
建立连接的3次握手过程: A: 我想和你建立连接,你收到我的请求吗?(我想娶你) B: 好的,我收到了你的请求,我们可以建立连接,我同意。(好的,我愿意嫁给你) A: 好的,我收到了你的回应,我…...

YOLOv5害虫识别项目代码打包完整上传Gitee仓库(已开源)以及git上传速率限制踩坑记录
YOLOv5害虫识别项目代码打包完整上传Gitee仓库(已开源)以及git上传速率限制踩坑记录 ps: 最近很多小伙伴需要这个害虫识别项目的源码,由于文件过大,所以将代码完整上传至gitee,所有文件、教程、论文、以及代码模型…...

从零开始学习c语言|21、动态内存管理
一、malloc函数 1、什么是malloc函数 malloc是memery(内存)和allocate(分配)的缩写,顾名思义,malloc函数为动态分配内存的意思 2、malloc函数语句 int *p(int *)malloc(sizeof(int))malloc函数的形参为申请的内存空间大小,上述申请了一个i…...
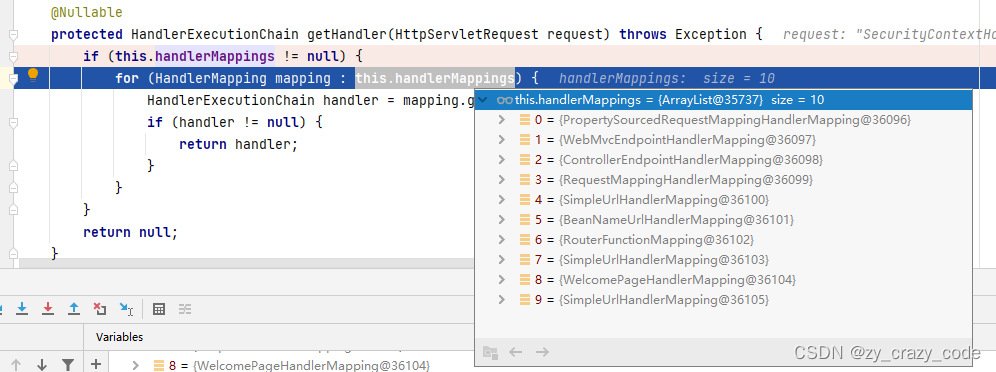
swagger关闭/v2/api-docs仍然可以访问漏洞
今天接到安全团队的说swagger有未授权访问漏洞,即使在swagger关闭的情况下http://127.0.0.1:8086/agcloud/v2/api-docs?group%E7%94%A8%E6%88%B7%E5%85%B3%E8%81%94%E4%BF%A1%E6%81%AF%E6%A8%A1%E5%9D%97仍然还能访问。 看了下原来是有写一个拦截器 registry.addI…...
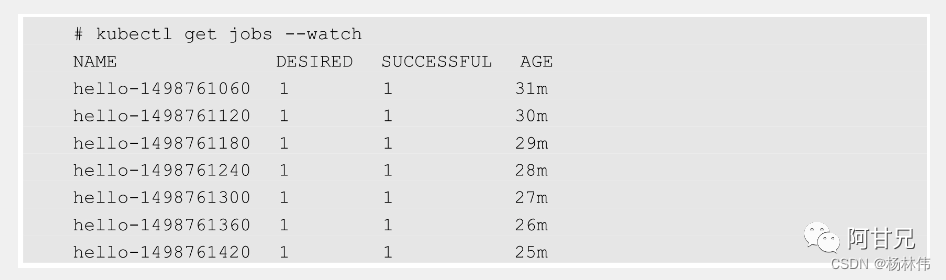
k8s pod调度总结
在Kubernetes平台上,我们很少会直接创建一个Pod,在大多数情况下会通过控制器完成对一组Pod副本的创建、调度 及全生命周期的自动控制任务,如:RC、Deployment、DaemonSet、Job 等。本文主要举例常见的Pod调度。1全自动调度功能&…...
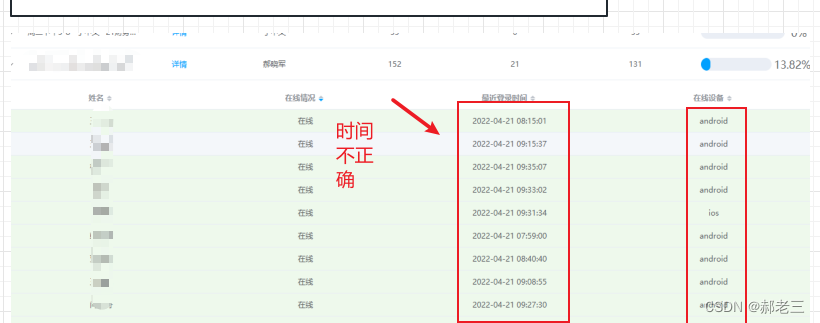
28个案例问题分析---10---对生产环境的敬畏--生产环境
一:背景介绍 1:上午9:23,老师没有进行上课,但是却又很多的在线人员,并且在线人员的时间也不正确。 2:开发人员及时练习用户,查看用户上课情况。 3:10点整,询问项目组长发…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...