机器学习 | 线性判别分析(Linear Discriminant Analysis)
1 机器学习中的建模
1.1 描述性建模
以方便的形式给出数据的主要特征,实质上是对数据的概括,以便在大量的或有噪声的数据中仍能观察到重要特征。重在认识数据的主要概貌,理解数据的重要特征。
- Task:聚类分析,数据降维,流形学习,密度估计,异常分析,可视化
1.2 预测性建模
以函数的形式给出感兴趣量(预测量)与可观测量之间的数量关系,实质上是根据观测到的对象特征来预测对象的其他特征。重在把握协变关系,据此进行预测。
- Task:分类(类别预测),回归(数值预测),评分(排名预测)
1.2.1 预测性建模方法
概率方法:生成式建模方法,借助训练数据对同类数据的生成机制(概率分布)进行估计,基于概率关系对变量取值进行概率预测。把模式视为随机变量的抽样,利用统计决策理论(贝叶斯统计)成熟的判决准则与方法,对模式样本进行分类
如:贝叶斯分类器、贝叶斯网络(概率图模型)、高斯混合模型、隐马尔可夫模型、受限玻尔兹曼机、生成对抗网络,变分自动编码器
代数方法:判别式建模方法,借助训练数据对观测量和预测量的函数关系进行直接建模,基于函数关系对变量取值进行数值预测。利用向量空间的直观概念,使用代数方程方法,对模式进行分类
如:KNN,感知机,判别分析,决策树,随机森林,支持向量机、逻辑回归,神经网络
1.3 判别函数
1.3.1 线性可分概念与线性分类算法
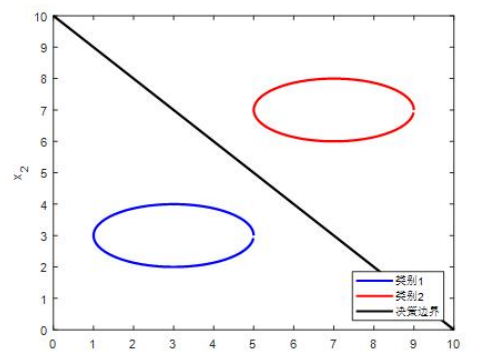
一个分类问题是否属于线性可分,取决于是否有可能找到一个点、直线、平面或超平面来分离开两个相邻的类别。如果每个类别样本的分布范围本身是全连通的单一凸集,且互不重叠,则这两个类别一定是线性可分的,如图所示。线性分类算法主要有线性判别函数、Fisher判别分析、单层感知器、逻辑回归等
1.3.2 判别函数的定义
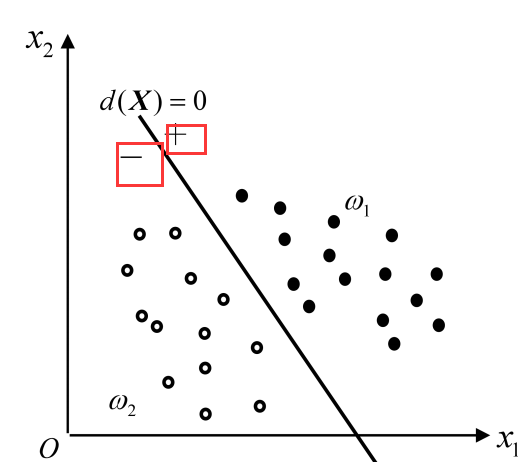
直接用来对模式进行分类的决策函数,若分属于ω1,ω2两类的n维模式在空间中的分布区域,可以用一代数方程d(X) =0决定的超平面作为分隔面,两类样本分布在分隔面的两侧,那么就称d(X)为判别函数(discriminant function)或称决策函数(decisionfunction)。代数方程d(X) =0表示的是n维空间的(n-1)维判决面 {或超平面(hyperplane)或超曲面(hypersurface) ,视d(x)形式而定}。
Note:这里的模式或许可以直接理解成数学里的自变量。
为了清晰地了解d(x)的含义,应该画出判别函数值d(x)这一轴,在没有画出的时候,就在自变量(模式)空间中画出d(x)取正负值的区域——这就是所谓判别面的正侧、负侧。
1.3.3 确定判别函数的两个因素
- 判决函数d(X)的函数形式:它可以是特征的线性或非线性的函数。
- 判决函数d(X)的系数:用所给的模式样本,通过优化准则确定。
主要关注线性判别函数,一个一般的n元线性函数应该具有什么的性质才适合做两分类和多分类的判别函数
2 线性判别函数
2.1 两类问题
在两类别情况下,判别函数 g (x) 具有以下性质:
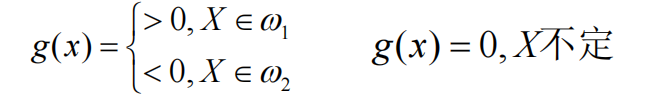
这是二维情况下判别由判别边界分类。情况如图:
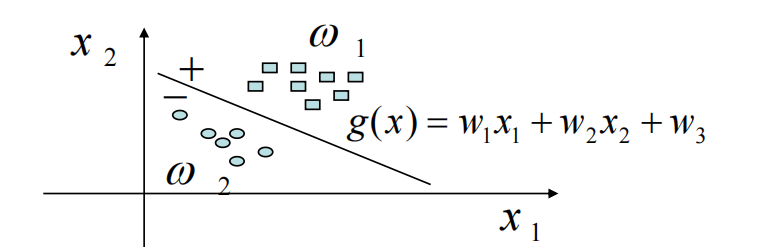
在n维情况下:
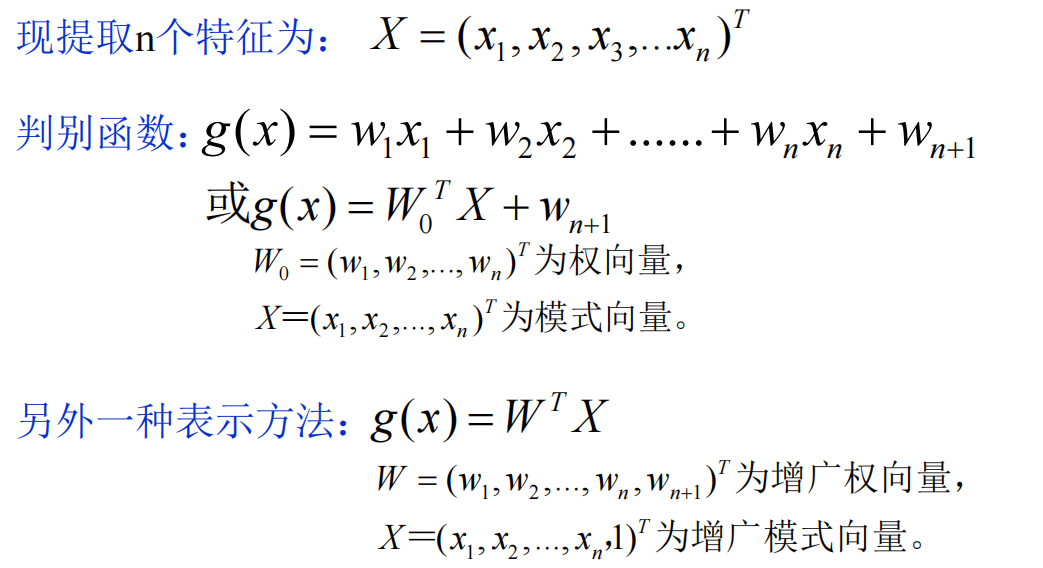
2.2 区别分类与回归两个概念
回顾:一元/多元线性回归(Multivariate linear regression)

w参数学习/训练出来之后,所确定的g(x)模型也叫预测模型。
若用g(x)预测的是离散值,此类学习任务称为“分类(Classification)” ;若用g(x)预测的是连续值,此类学习任务称为“回归(regression)”。由于这里g(x)是线性的,故称为多元线性回归
离散值预测->分类, 连续值预测->回归
2.3 多类问题
对于多类问题,模式有 ω1 ,ω2 , … , ωm 个类别。可分三种情况讨论:
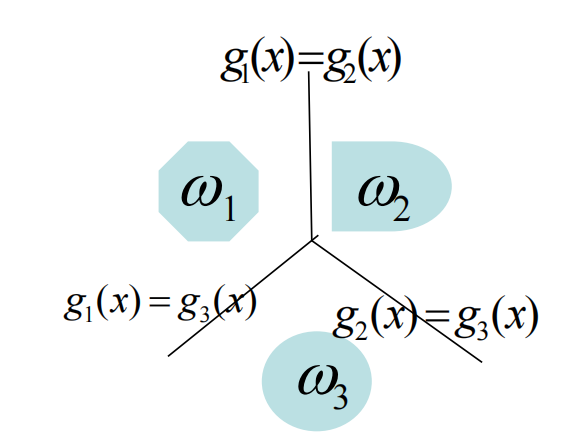
2.3.1 ω i / ω ˉ i \omega_i / \bar{\omega}_i ωi/ωˉi多类情况1 (是非两分法)
每一模式类与其他模式类间可用单个判别平面把一个类分开。这种情况,M类可有M个判别函数,且具有以下性质:
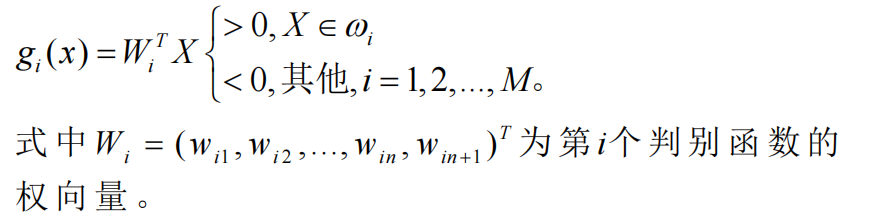
理解:
每一类别可用单个判别边界与其他类别分开。若一模式X属于ω1,则由图可清楚看出:这时g1(x) >0而g2(x) <0 , g3(x) <0 。 ω1 类与其他类之间的边界由g1(x)=0确定。模式属于哪一类,对应的那一类的判别函数值就大于0。
特殊情况:
2.3.2 ω i / ω j \omega_i / {\omega}_j ωi/ωj多类情况2(成对两分法)
每两个模式类间可用判别平面分开(即模式类成对可分)。

2.3.3 多类情况3: ω i / ω j \omega_i / {\omega}_j ωi/ωj 成对两分法(无IR区)

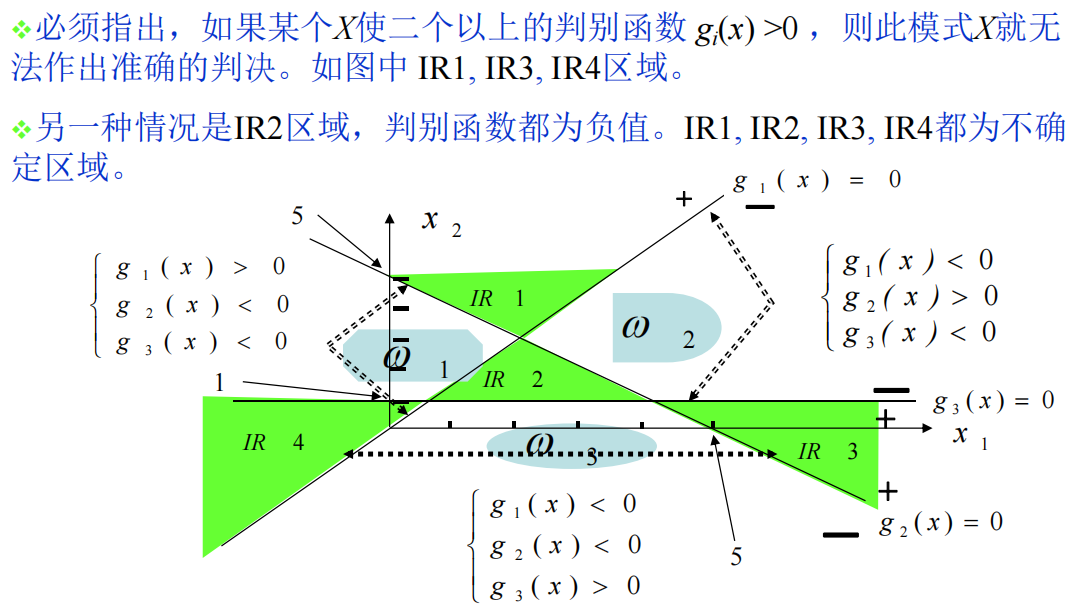
多类情况3下的一个示例:不存在IR区域,IR不确定区没有了,所以这种是最好的情况。
2.4 线性判别函数的性质
- 模式空间与加权空间:由于假设权向量W与模式向量X的内积为零(g(x)=0),故W与分界面H正交

相关文章:

机器学习 | 线性判别分析(Linear Discriminant Analysis)
1 机器学习中的建模 1.1 描述性建模 以方便的形式给出数据的主要特征,实质上是对数据的概括,以便在大量的或有噪声的数据中仍能观察到重要特征。重在认识数据的主要概貌,理解数据的重要特征。 Task:聚类分析,数据降…...

TypeScript-数组、函数类型
1.数组类型 1.1类型 方括号 let arry:number[][5,2,0,1,3,1,4] 1.2 数组泛型 let arry2:Array<number>[5,2,0,1,3,1,4] 1.3接口类型 interface makeArryRule{[index:number]:number }let arry3:makeArryRule[5,2,0,1,3,1,4] 1.4伪数组 说明: argument…...
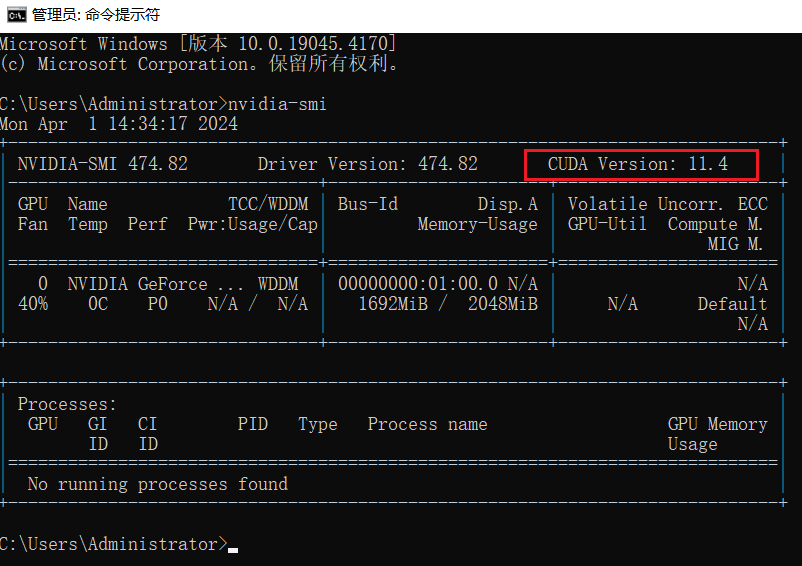
Python深度学习034:cuda的环境如何配置
文章目录 1.安装nvidia cuda驱动CMD中看一下cuda版本:下载并安装cuda驱动2.创建虚拟环境并安装pytorch的torch_cuda3.测试附录1.安装nvidia cuda驱动 CMD中看一下cuda版本: 注意: 红框的cuda版本,是你的显卡能装的最高的cuda版本,所以可以选择低于它的版本。比如我的是11…...
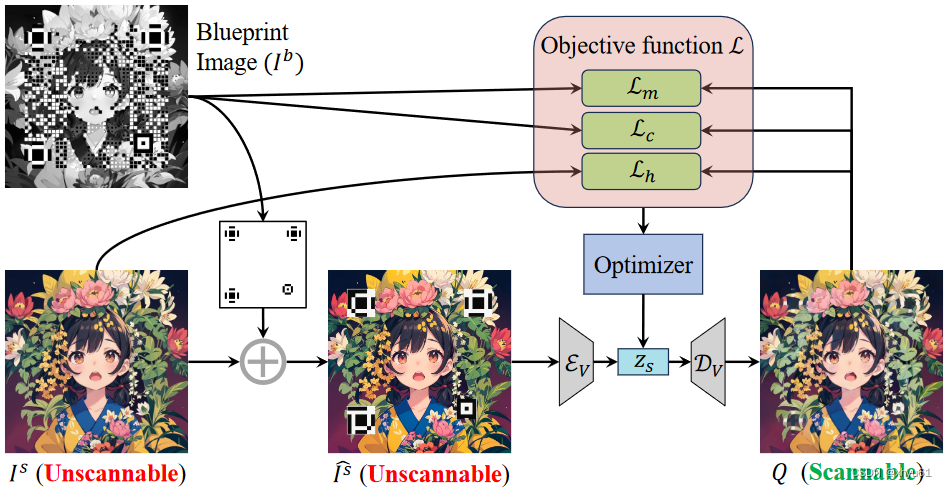
【论文笔记】Text2QR
论文:Text2QR: Harmonizing Aesthetic Customization and Scanning Robustness for Text-Guided QR Code Generation Abstract 二维码通常包含很多信息但看起来并不美观。stable diffusion的出现让平衡扫描鲁棒性和美观变为可能。 为了保证美观二维码的稳定生成&a…...
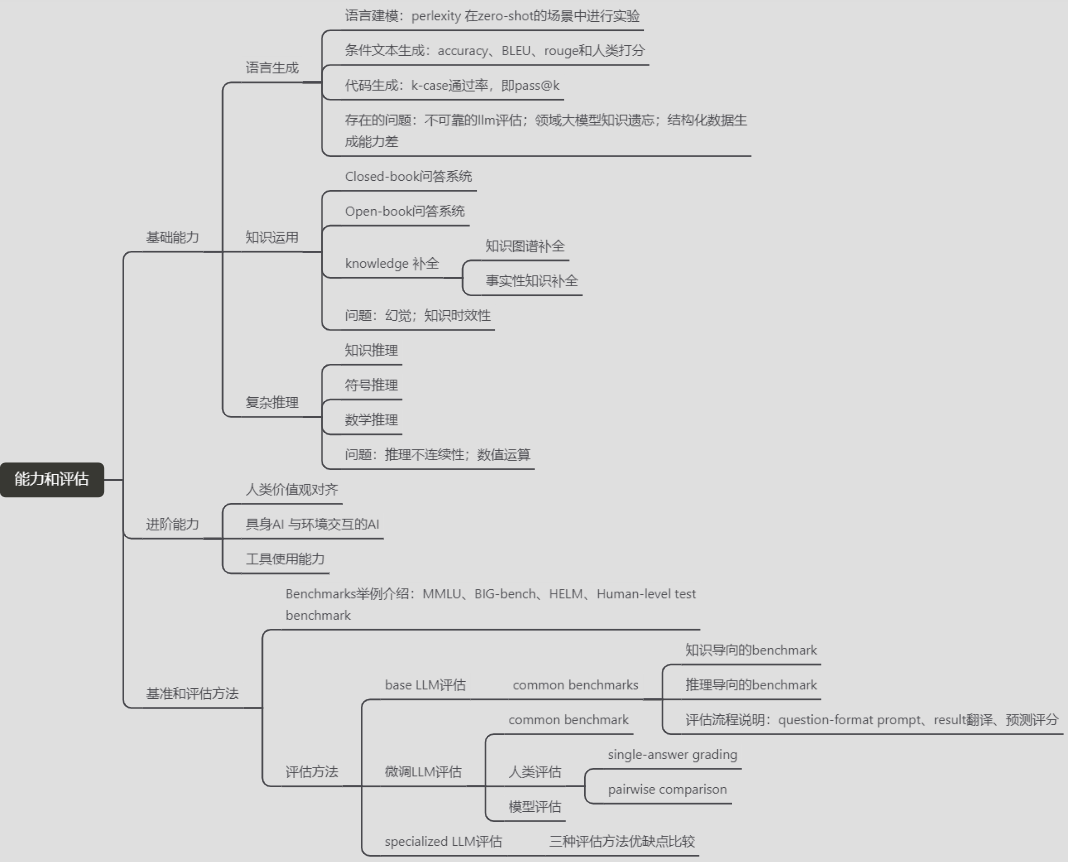
【ReadPapers】A Survey of Large Language Models
LLM-Survey的llm能力和评估部分内容学习笔记——思维导图 思维导图 参考资料 A Survey of Large Language Models论文的github仓库...

站群CMS系统
站群CMS系统是一种用于批量建立和管理网站的内容管理系统,它能够帮助用户快速创建大量的网站,并实现对这些网站的集中管理。以下是三个在使用广泛的站群CMS系统,它们各具特色,可以满足不同用户的需求。 1. Z-BlogPHP Z-BlogPHP是…...

landsat8数据产品说明
1、下载数据用户手册 手册下载网址,搜索landsat science关键词,并点击到官网下载。 2、用户手册目录 3、landsat8数据产品说明 具体说明在手册的第四章,4.1.4数据产品章节,具体描述如下: 英文意思: L8 的…...
Golang 内存管理和垃圾回收底层原理(二)
一、这篇文章我们来聊聊Golang内存管理和垃圾回收,主要注重基本底层原理讲解,进一步实战待后续文章 垃圾回收,无论是Java 还是 Golang,基本的逻辑都是基于 标记-清理 的, 标记是指标记可能需要回收的对象,…...

OpenHarmony:全流程讲解如何编写ADC平台驱动以及应用程序
ADC(Analog to Digital Converter),即模拟-数字转换器,可将模拟信号转换成对应的数字信号,便于存储与计算等操作。除电源线和地线之外,ADC只需要1根线与被测量的设备进行连接。 一、案例简介 该程序是基于…...

计算机学生求职简历的一些想法
面试真的是一件非常难的事情,因为在短短的半小时到一个小时,来判断一个同学行不行,其实是很不全面的。作为一个求职的同学应该怎么办呢?求职的同学可以提前做一些准备,其中比较重要的要数简历的编写。 简历的作用 简…...

网工内推 | 售前专场,需熟悉云计算技术,上市公司,提成高
01 神州数码 招聘岗位:售前工程师 职责描述: 1.负责所在区域华为IT产品线(服务器、存储、云、虚拟化)的售前技术支持工作,包括客户交流、方案编写、配置报价、投标支持、测试等; 2.与厂商相关人员建立和保…...
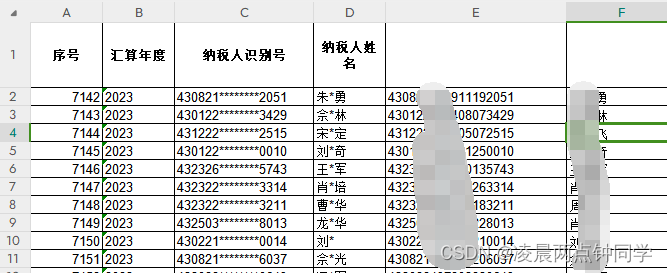
excel匹配替换脱敏身份证等数据
假如excel sheet1中有脱敏的身份证号码和姓名,如: sheet2中有未脱敏的数据数据 做法如下: 1、在sheet2的C列用公式 LEFT(A2,6)&REPT("*",8)&RIGHT(A2,4) 做出脱敏数据,用来与sheet1的脱敏数据匹配 2、在sheet…...
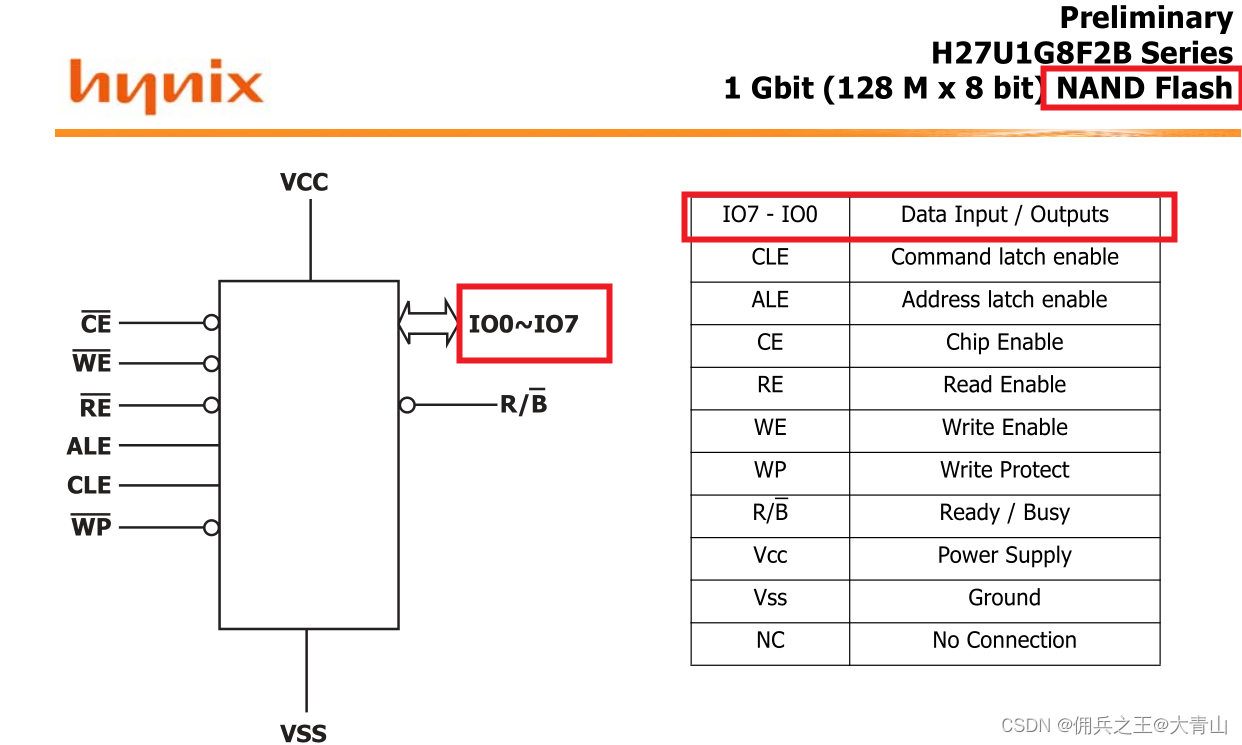
[技术笔记] Flash选型之基础知识芯片分类
1、按照接口分类 分为 Serial串口Flash 和 Parallel并口Flash; 市场大量使用Serial Flash;价格便宜;已满足系统对数据读写速度的要求; Serial Flash已经可以代表 NOR Flash; 小知识: 1)在…...

Jenkins常用插件安装及全局配置
Jenkins常用插件安装及全局配置 前言 Jenkins是一个流行的持续集成工具,通过安装适用的插件,可以扩展Jenkins的功能,并与其他工具和系统集成。本文将介绍一些常用的Jenkins插件以及安装和配置的步骤。通过安装和配置这些常用插件…...

C++初学者:如何优雅地写程序
我喜欢C语言的功能强大,简洁,我也喜欢C#的语法简单,清晰,写起来又方便好用。 一、为什么不用C语言写程序。 C语言用来做题目,考试研究是很方便的,但是用来写程序做软件,你就会发现,…...

图论- 最小生成树
一、最小生成树-prim算法 1.1 最小生成树概念 一幅图可以有很多不同的生成树,比如下面这幅图,红色的边就组成了两棵不同的生成树: 对于加权图,每条边都有权重(用最小生成树算法的现实场景中,图的边权重…...
LeetCode刷题记(一):1~30题
1. 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以…...
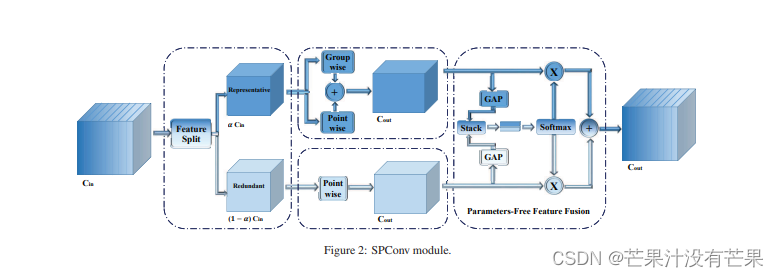
芒果YOLOv5改进89:卷积SPConv篇,即插即用,去除特征图中的冗余,FLOPs 和参数急剧下降,提升小目标检测
芒果专栏 基于 SPConv 的改进结构,改进源码教程 | 详情如下🥇 👉1. SPConv 结构、👉2. CfSPConv 结构 💡本博客 改进源代码改进 适用于 YOLOv5 按步骤操作运行改进后的代码即可 即插即用 结构。博客 包括改进所需的 核心结构代码 文件 YOLOv5改进专栏完整目录链接:…...
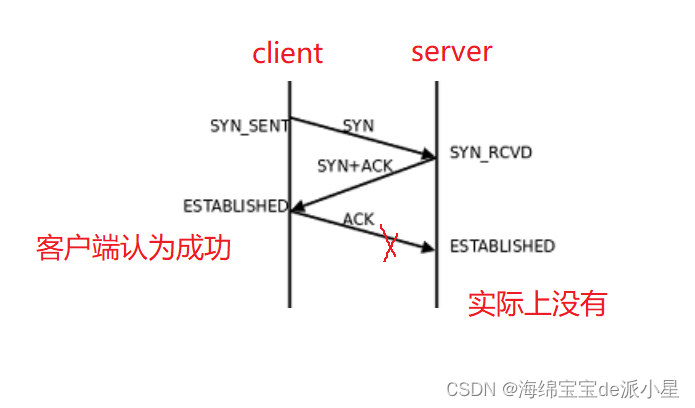
Linux:详解TCP报头类型
文章目录 温习序号的意义序号和确认序号报文的类型 TCP报头类型详解ACK: 确认号是否有效SYN: 请求建立连接; 我们把携带SYN标识的称为同步报文段FIN: 通知对方, 本端要关闭了PSH: 提示接收端应用程序立刻从TCP缓冲区把数据读走RST: 对方要求重新建立连接; 我们把携带RST标识的称…...
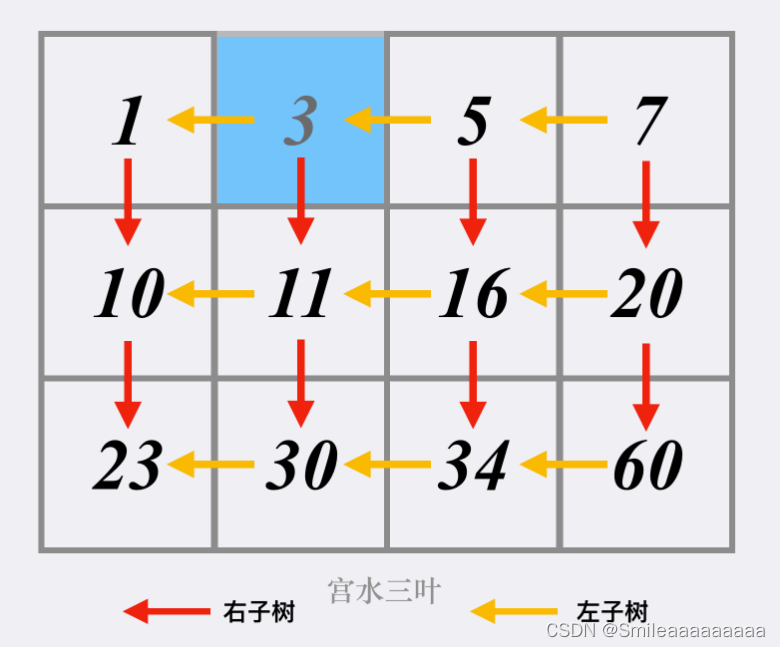
【Leetcode】top 100 二分查找
35 搜索插入位置 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。 基础写法!!!牢记…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
