代码随想录刷题day42| 01背包理论基础分割等和子集
文章目录
- day41学习内容
- 一、 01背包之二维数组解法
- 1.1、什么是01背包
- 1.2、动态规划五部曲
- 1.2.1、 确定dp数组(dp table)以及下标的含义
- 1.2.2、确定递推公式
- 1.2.3、 dp数组如何初始化
- 1.2.4、确定遍历顺序
- 1.2.5、计算并返回最终结果
- 二、 01背包之一维数组解法
- 2.1、动态规划五部曲
- 2.1.1、 确定dp数组(dp table)以及下标的含义
- 2.1.2、确定递推公式
- 2.1.3、 dp数组如何初始化
- 2.1.4、确定遍历顺序
- 二维动态规划
- 从二维到一维的转化
- 为什么要逆序更新
- 具体示例
- 三、 分割等和子集
- 3.1、动态规划五部曲
- 3.1.1、 确定dp数组(dp table)以及下标的含义
- 3.1.2、确定递推公式
- 3.1.3、 dp数组如何初始化
- 3.1.4、确定遍历顺序
- 3.1.5、计算并返回最终结果
- 1.3、代码
- 总结
- 1.感想
- 2.思维导图
day41学习内容
day41主要内容
- 01背包之二维数组解法
- 01背包之一维数组解法
- 分割等和子集
声明
本文思路和文字,引用自《代码随想录》
一、 01背包之二维数组解法
1.1、什么是01背包
1.2、动态规划五部曲
1.2.1、 确定dp数组(dp table)以及下标的含义
- 考虑前i个物品,当背包容量为j时的最大价值。或者说
- 从物品0到i之间,任意取一个物品放到重量为j的背包中的最大价值
1.2.2、确定递推公式
在0-1背包问题中,dp[i][j]通常表示在考虑前i个物品,且背包容量为j时,能够获得的最大价值。当我们在处理第i个物品时,面临的选择是:放入这个物品,或者不放入这个物品。
在0-1背包问题中,递推公式通常写为:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
其中:
dp[i][j]:考虑前i个物品,当背包容量为j时的最大价值。dp[i-1][j]:不放入第i个物品时,考虑前i-1个物品,背包容量为j的最大价值。- 如果选择不放入第
i个物品,那么背包中的物品组合应该与考虑前i-1个物品时背包容量为j的情况相同。因为我们没有使用额外的容量来放置第i个物品,所以背包的容量和内容保持不变,相当于在做决策时忽略了第i个物品。 - 因此,此时的公式为,
dp[i-1][j],表示的是在不选择第i个物品的情况下,考虑前i-1个物品时能够获得的最大价值。这反映了一个关键的动态规划概念,即利用子问题的解来构建更大问题的解。
- 如果选择不放入第
dp[i-1][j-w[i]] + v[i]:放入第i个物品时的情况,这里w[i]是第i个物品的重量,v[i]是第i个物品的价值。这表示,如果放入第i个物品,那么背包剩余容量为j-w[i],对应的最大价值应加上第i个物品的价值v[i]。
1.2.3、 dp数组如何初始化
在01背包问题中,dp[i][j]表示在前i个物品中选择一些物品,使得这些物品的总重量不超过j时,这些物品的最大总价值。因此,dp[0][j]表示当没有物品可以选择时,任何容量j的背包的最大价值都是0,因为我们什么也装不进去。同样地,dp[i][0]表示当背包的容量为0时,不论有多少物品可供选择,我们都无法装入任何物品,所以最大总价值为0。
1.2.4、确定遍历顺序
从前向后遍历,没啥好说的
1.2.5、计算并返回最终结果
无
二、 01背包之一维数组解法
2.1、动态规划五部曲
2.1.1、 确定dp数组(dp table)以及下标的含义
- dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2.1.2、确定递推公式
直接给结论:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
2.1.3、 dp数组如何初始化
dp[0] = [0]
2.1.4、确定遍历顺序
需要逆序遍历。
二维动态规划
假设我们有两个物品,其中:
- 物品1的重量为
w[1] = 2,价值为v[1] = 3; - 物品2的重量为
w[2] = 3,价值为v[2] = 4; - 背包的总容量为
W = 5。
我们使用二维数组dp[i][j]来表示考虑到第i个物品时,背包容量为j的最大价值。
初始化dp[0][j] = 0,因为没有物品时价值为0。对于每个物品i,我们遍历所有可能的背包容量j,更新dp[i][j]。
从二维到一维的转化
关键点在于观察到更新dp[i][j]时,只需要前一行的信息,即dp[i-1][...]。因此,如果我们能确保在更新dp[j]时,dp[j-w[i]]总是代表加入当前物品前的状态,那么我们就可以只用一维数组来保存所有需要的信息。
为什么要逆序更新
假设我们正向更新,即j从小到大更新。当我们更新dp[j]时,dp[j-w[i]]可能已经被当前物品的加入更新过了,这意味着我们可能会错误地将同一个物品加入背包多次。
逆序更新(即j从大到小更新)确保在更新dp[j]时,dp[j-w[i]]还没有被当前物品的加入影响,因为我们还没有到达更小的j值。这样,每个物品只会被考虑加入一次。
具体示例
让我们以背包总容量W = 5为例,来具体分析这个过程。假设我们现在处理物品1(重量2,价值3)。
-
在二维动态规划中,我们可能得到类似
dp[1][j]的更新,其中j从1到5。 -
转换为一维后,我们同样需要更新
dp[j],但是逆序处理。
对于物品1,初始dp为[0, 0, 0, 0, 0, 0](考虑容量从0到5)。
-
正向考虑,如果我们先更新
dp[2]为3(加入物品1),当我们到达dp[4]时,可能错误地再次考虑加入物品1,因为它看到的dp[2]已经反映了物品1的加入。 -
逆序更新,我们从
dp[5]开始往回看。当更新dp[5]时,dp[3](对应j-w[i])还未被更新,确保我们正确地只考虑加入物品1一次。
三、 分割等和子集
416.原题链接
3.1、动态规划五部曲
3.1.1、 确定dp数组(dp table)以及下标的含义
- ,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
3.1.2、确定递推公式
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
3.1.3、 dp数组如何初始化
dp[0] = 0,java中新建数组,会自动赋值所有的元素的值都为0
3.1.4、确定遍历顺序
逆序遍历
3.1.5、计算并返回最终结果
return dp[target] == target;
1.3、代码
class Solution {public boolean canPartition(int[] nums) {if(nums == null || nums.length == 0) return false;int n = nums.length;int sum = 0;for(int num : nums) {sum += num;}//总和为奇数,不能平分if(sum % 2 != 0) return false;int target = sum / 2;//开始背包逻辑int[] dp = new int[target + 1];for(int i = 0; i < n; i++) {for(int j = target; j >= nums[i]; j--) {// 此时价值为nums[i],重量也为nums[i]dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[target] == target;}
}
总结
1.感想
- 好难好难。。。
2.思维导图
本文思路引用自代码随想录,感谢代码随想录作者。
相关文章:

代码随想录刷题day42| 01背包理论基础分割等和子集
文章目录 day41学习内容一、 01背包之二维数组解法1.1、什么是01背包1.2、动态规划五部曲1.2.1、 确定dp数组(dp table)以及下标的含义1.2.2、确定递推公式1.2.3、 dp数组如何初始化1.2.4、确定遍历顺序1.2.5、计算并返回最终结果 二、 01背包之一维数组…...

Python文件操作命令
文件操作 我知道你最近很累,是那种看不见的、身体上和精神上的疲惫感,但是请你一定要坚持下去。就算无人问津也好,技不如人也好,千万别让烦躁和焦虑毁了你的热情和定力。别贪心,我们不可能什么都有,也别灰心…...
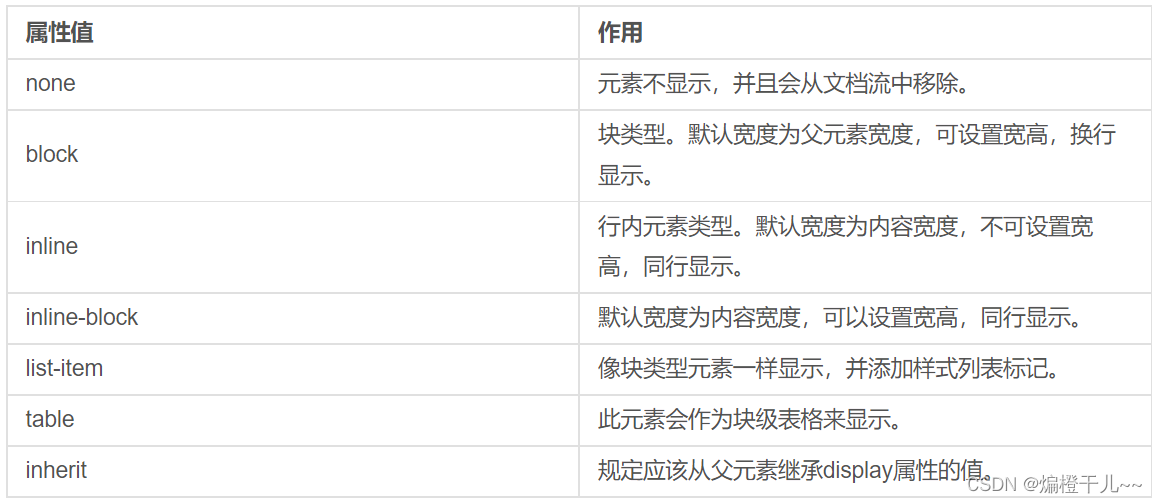
CSS面试题---基础
1、css选择器及优先级 选择器优先级:内联样式>id选择器>类选择器、属性选择器、伪类选择器>标签选择器、微元素选择器 注意: !important优先级最高; 如果优先级相同,则最后出现的样式生效; 继承得到的样式优先…...

OpenHarmony实战开发-分布式数据管理
介绍 本示例展示了在eTS中分布式数据管理的使用,包括KVManager对象实例的创建和KVStore数据流转的使用。 通过设备管理接口ohos.distributedDeviceManager ,实现设备之间的kvStore对象的数据传输交互,该对象拥有以下能力详见 ;1、注册和解…...
微服务(基础篇-007-RabbitMQ部署指南)
目录 05-RabbitMQ快速入门--介绍和安装_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1LQ4y127n4?p65&vd_source60a35a11f813c6dff0b76089e5e138cc 1.单机部署 1.1.下载镜像 1.2.安装MQ 2.集群部署 2.1.集群分类 2.2.设置网络 视频地址: 05-Rab…...
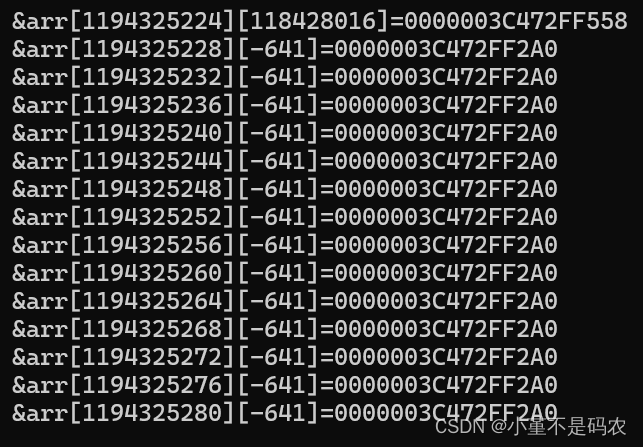
C语言一维数组及二维数组详解
引言: 小伙伴们,我发现我正文更新的有些慢,但相信我,每一篇文章真的都很用心在写的,哈哈,在本篇博客当中我们将详细讲解一下C语言中的数组知识,方便大家后续的使用,有不会的也可以当…...

11.图像边缘检测的原理与实现
数字图像处理(19): 边缘检测算子(Roberts算子、Prewitt算子、Sobel算子 和 Laplacian算子) 数字图像处理(20): 边缘检测算子(Canny算子) 1.边缘检测介绍 1.1 边缘检测的基本原理 边缘是图像的基本特征,所谓的边缘就是指的图像的局部不连续性。灰度或者结构等信息的…...

RVM安装ruby笔记
环境 硬件:Macbook Pro 系统:macOS 14.1 安装公钥 通过gpg安装公钥失败,报错如下: 换了几个公钥地址(hkp://subkeys.pgp.net,hkp://keys.gnupg.net,hkp://pgp.mit.edu),…...

电力系统负荷预测方法
电力系统负荷是什么? 所谓的电力负荷预测是指以电力负荷变化以及外界因素变化为基础,以特定的数学方法或者建立数学模型的方式为手段,通过对电力负荷历史数据进行分析,对电力系统的需求做出估计以及研究相关因素对电力负荷的影响…...
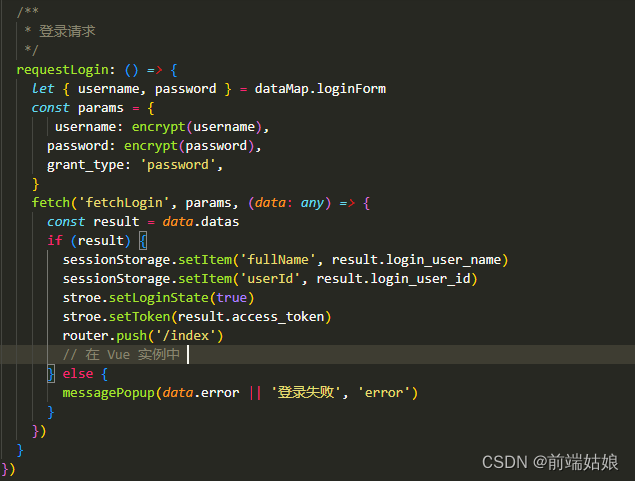
electron打包桌面版.exe之vue项目踩坑(vue3+electron 解决打包后首页打开空白,打包后路由不跳转及请求不到后端数据等问题)
vue项目https://www.qingplus.cn/components-web/index打包桌面版问题集合 一、静态资源加载问题 npm run electron_dev桌面版运行后页面空白,内容未加载。 填坑: 打包配置要用相对路径 vite.config.ts文件中的base要改成./,之前加了项目…...
)
MySQL学习笔记(持续更行ing)
级别: 1. 了解,面试概率10% 2. 掌握,面试概率50% 3. 重点,面试概率80% 目录 1. 数据库**** 1.1. 概念**** 1.2. 分类**** 1.2.1. 关系型数据库**** 1.2.1.1. SQL**** 1.2.2. 安装**** 1.2.2.1. Navicat**** 1.2.3. 非…...

服务器配置Huggingface并git clone模型和文件
服务器配置Huggingface并git clone模型和文件 参考:https://huggingface.co/welcome 1 注册hugging face 官网注册,并获取token【https://huggingface.co/settings/tokens】,用于登录 2 安装 2.1 安装lfs https://stackoverflow.com/qu…...

Rust 开发的高性能 HTTP 请求工具
一、简述 在现在的软件开发领域,HTTP请求的快速验证变得越来越重要。特别是对于后端开发人员和测试工程师来说,能够快速创建、执行并验证HTTP请求对于提升开发效率至关重要。近期有一个名为Hurl的开源项目,它被设计来高效执行HTTP请求&#…...

Android Studio 通过 WIFI 调试手机 app
操作流程 首先第一步,PC 和手机都需要连在同一个局域网 WIFI。 第二步,手机 USB 连上 PC,确保能查看到通过 USB 连上的设备: >>adb devices List of devices attached CSXasjdhwjqwjhqdh device (最好只看到一个连上的设置…...
RabbitMQ高级笔记
视频链接:【黑马程序员RabbitMQ入门到实战教程】 文章目录 1.发送者的可靠性1.1.生产者重试机制1.2.生产者确认机制1.3.实现生产者确认1.3.1.开启生产者确认1.3.2.定义ReturnCallback1.3.3.定义ConfirmCallback 2.MQ的可靠性2.1.数据持久化2.1.1.交换机持久化2.1.2.…...

【Qt】QtCreator交叉编译环境配置Qt mkspec
1、问题描述 在QtCreator中配置TI AM437x的交叉编译环境后,编译时报错,错误信息如下 error: gnu/stubs-soft.h: No such file or directory2、原因分析 1)环境变量CC 搜索网络,解决方法为修改交叉编译工具目录下环境配置脚本,即执行source时的文件。 本人环境为:linux…...
点点数据K参数加密逆向分析(RPC方案跟加密算法还原)
文章目录 1. 写在前面2. 接口分析3. 断点分析4. RPC调用5. 算法还原 【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长…...

考研数学|《1800》+《660》精华搭配混合用(经验分享)
肯定不行,考研数学哪有这么容易的! 先说说这两本习题册,李永乐老师推出的新版660题,相较于18年前的版本,难度略有降低,更加适合初学者。因此,对于处于基础阶段的学习者来说,新版660…...
)
【Redis 二】Redis客户端(Jedis、SpringDataRedis、RedisTemplate)
1. Redis客户端 Jedis 以redis命令作为方法名称,学习成本低,但是Jedis实例是线程不安全的,多线程环境下需要基于连接池来使用(必须为每个线程分配独立的Jedis连接) lettuce 基于Netty实现,支持同步、异步和…...

Java中Filter和Interceptor的区别
概述 本文阐述Java中Filter和Interceptor的区别。 执行顺序不同 FIlter->Servlet->Interceptor->Controller 配置方式不同 FIlter在web.xml中配置 Interceptor在spring中的配置文件中、使用注解 是否依赖servlet Filter依赖servlet,而Interceptor不…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
