10.图像高斯滤波的原理与FPGA实现思路
1.概念
高斯分布
图像滤波之高斯滤波介绍
图像处理算法|高斯滤波
高斯滤波(Gaussian filter)包含很多种,包括低通、高通、带通等,在图像上说的高斯滤波通常是指的高斯模糊(Gaussian Blur),是一种高斯低通滤波。通常这个算法也可以用来模糊图像,提供模糊滤镜。也可以用来过滤自然界的高斯白噪声。
高斯分布(正态分布)是一个常见的连续概率分布,正态分布的数学期望值或期望值 μ \mu μ等于位置参数,决定了分布的位置,其方差 σ 2 \sigma^2 σ2的开平方或者标准差 σ \sigma σ等于尺度参数,决定了分布的幅度。正态分布的概率密度函数曲线呈钟形,所以又被称为钟形曲线。我们常说的标准正态分布是位置参数 μ = 0 , 方差 σ 2 = 1 \mu=0,方差\sigma^2=1 μ=0,方差σ2=1的正态分布。
若随机变量 X X X服从一个位置参数为 μ 、方差为 σ 2 \mu、方差为\sigma^2 μ、方差为σ2的正态分布,可以记为 X N ( μ , σ 2 ) X~N(\mu,\sigma^2) X N(μ,σ2),其概率密度函数为:
g ( x ) = 1 2 π σ e ( − ( x − μ ) 2 2 σ 2 ) (1) g(x)=\frac{1} {\sqrt{2\pi} \sigma }e^{(-\frac{{(x-\mu)}^{2} }{2\sigma^{2}})}\tag{1} g(x)=2πσ1e(−2σ2(x−μ)2)(1)
高斯滤波器是一种根据高斯函数的形状来选择权值的线性平滑滤波器,对于抑制服从正态分布的噪声非常有效,一维零均值高斯函数为:
g ( x ) = 1 2 π σ e − x 2 2 σ 2 (2) g(x)=\frac{1} {\sqrt{2\pi} \sigma }e^{-\frac{x^{2} }{2\sigma^{2}}}\tag{2} g(x)=2πσ1e−2σ2x2(2).
其中,高斯分布参数( σ \sigma σ)决定了高斯函数的宽度,一维高斯函数的图形如下图:

二维高斯高斯分布的函数为:
g ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 (3) g(x,y)=\frac{1}{2\pi\sigma^2}e^{\frac{-x^2+y^2}{2\sigma^2}}\tag{3} g(x,y)=2πσ21e2σ2−x2+y2(3)
二维高斯分布的图像为:

2.高斯滤波性质
高斯函数具有五个重要的性质,这些性质使得它在早期图像处理中特别有用.这些性质表明,高斯平滑滤波器无论在空间域还是在频率域都是十分有效的低通滤波器,且在实际图像处理中得到了工程人员的有效使用.高斯函数具有五个十分重要的性质,它们是:
1.二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的.一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向.
2.高斯函数是单值函数.这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的.这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真.
3.高斯函数的傅立叶变换频谱是单瓣的.正如下面所示,这一性质是高斯函数付立叶变换等于高斯函数本身这一事实的直接推论.图像常被不希望的高频信号所污染(噪声和细纹理).而所希望的图像特征(如边缘),既含有低频分量,又含有高频分量.高斯函数付立叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染,同时保留了大部分所需信号.
4.高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的.σ越大,高斯滤波器的频带就越宽,平滑程度就越好.通过调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷.
5.由于高斯函数的可分离性,较大尺寸的高斯滤波器可以得以有效地实现.二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同一维高斯函数卷积.因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长.
3.高斯滤波的原理与实现
高斯滤波既能用来过滤高斯噪音,也可用来做高斯模糊。
要模糊一张图像,可以直接用均值滤波来做简单的模糊,但是这样做显然不大合理,因为图像是连续的,离卷积核中心的点关系更加密切,越远的点关系越疏远,这个时候就需要加权平均。明显的离中心点越近的像素点权重越大。而正态分布显然是一种可取的权重分配方式,又由于图像是二维的,所以需要使用二维的高斯函数。所以高斯滤波的本质是利用高斯函数来生成高斯核(高斯卷积模板)来对图像进行卷积操作。
理论上高斯分布在所有定义域上都有非负值,这就需要一个无限大的卷积核,但是实际上,仅需要取均值的三倍标准差(即 3 σ 3\sigma 3σ)内的值,以外的部分去掉即可。
高斯滤波最重要的就是找到高斯模板然后进行卷积,以3X3高斯模板为例,假设中心点的坐标为(0,0),根据二维高斯函数 g ( x , y ) g(x,y) g(x,y),还需要设定 σ \sigma σ的值,假定 σ = 0.8 \sigma=0.8 σ=0.8(这个值不宜过大,否则就会变成均值滤波),可以根据坐标值来算出对应的高斯模板。
假定中心点的坐标为(0,0),那么距离它最近的八个点的坐标如下:

将坐标以及设定的 σ \sigma σ带入二维高斯函数中,可以得到对应点的坐标的权重如下:

为了防止高斯滤波后的图像偏亮或者偏暗,我们还需要对图像进行归一化,这九个点的权重和等于0.9125991,因此需要分别对这九个数除以0.9125991,最终得到的高斯模板为:

有了高斯模板就可以对图像进行卷积了,但是在FPGA中对于小数的运算不友好,于是我们将这个3X3模板扩大了16倍,得到了近似的整数模板,卷积完成后再除以16来做定浮点数的近似计算。16倍后的模板高斯卷积模板为:

3X3的高斯模板生成与定浮点数的MATLAB算法实现为:
clear;
clc;
close all;
sigma = 0.8 ;
A = exp(-(1+1)/(2*sigma*sigma))/(2*pi*sigma*sigma);
B = exp(-(1+0)/(2*sigma*sigma))/(2*pi*sigma*sigma);
C = exp(-(0+0)/(2*sigma*sigma))/(2*pi*sigma*sigma);
D = A*4 + B*4 + C;gauss_double = [A,B,A;B,C,B;A,B,A];
gauss_normal = gauss_double / sum(sum(gauss_double));
gauss_integer = floor(gauss_normal/gauss_normal(1,1));
生成卷积模板后的FPGA实现这里就不作过多介绍了,参考前几章的3X3卷积核以及均值滤波的实现方式改变参数即可。
相关文章:

10.图像高斯滤波的原理与FPGA实现思路
1.概念 高斯分布 图像滤波之高斯滤波介绍 图像处理算法|高斯滤波 高斯滤波(Gaussian filter)包含很多种,包括低通、高通、带通等,在图像上说的高斯滤波通常是指的高斯模糊(Gaussian Blur),是一种高斯低通滤波。通常这个算法也可以用来模…...

WebGIS 地铁交通线网 | 图扑数字孪生
数字孪生技术在地铁线网的管理和运维中的应用是一个前沿且迅速发展的领域。随着物联网、大数据、云计算以及人工智能技术的发展,地铁线网数字孪生在智能交通和智慧城市建设中的作用日益凸显。 图扑软件基于 HTML5 的 2D、3D 图形渲染引擎,结合 GIS 地图…...
Docker 哲学 - push 本机镜像 到 dockerhub
注意事项: 1、 登录 docker 账号 docker login 2、docker images 查看本地镜像 3、注意的是 push镜像时 镜像的tag 需要与 dockerhub的用户名保持一致 eg:本地镜像 express:1 直接 docker push express:1 无法成功 原因docker不能识别 push到哪里 …...
大数据学习第十二天(hadoop概念)
1、服务器之间数据文件传递 1)服务器之间传递数据,依赖ssh协议 2)http协议是web网站之间的通讯协议,用户可已通过http网址访问到对应网站数据 3)ssh协议是服务器之间,或windos和服务器之间传递的数据的协议…...
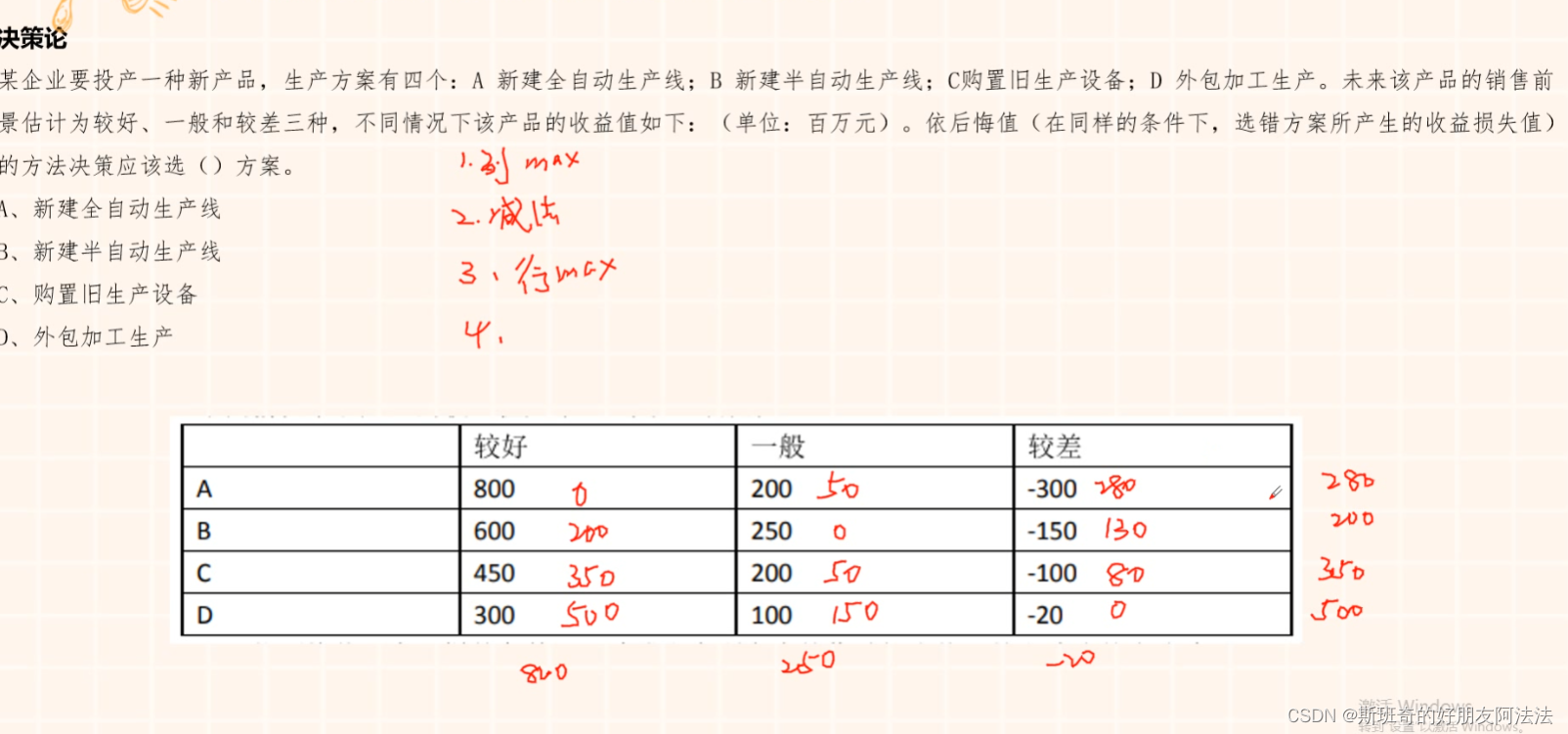
管理科学笔记
1.线性规划 画出区域,代入点计算最大最小值 2.最小生成树 a.断线法,从大的开始断 b.选择法,从小的开始选 3.匈牙利法 维度数量直线覆盖所有的0 4.一直选最当前路线最短路径 5.线性规划 6.决策论...

WebKit结构简介
WebKit是一款开源的浏览器引擎,用于渲染网页内容。它负责将HTML、CSS和JavaScript等网络资源转换为用户在屏幕上看到的图形界面。WebKit是一个跨平台的引擎,可以在多种操作系统上运行,如Windows、macOS、Linux等。 以下是一篇关于WebKit结构…...

Kaggle:收入分类
先看一下数据的统计信息 import pandas as pd # 加载数据(保留原路径,但在实际应用中建议使用相对路径或环境变量) data pd.read_csv(r"C:\Users\11794\Desktop\收入分类\training.csv", encodingutf-8, encoding_errorsrepl…...
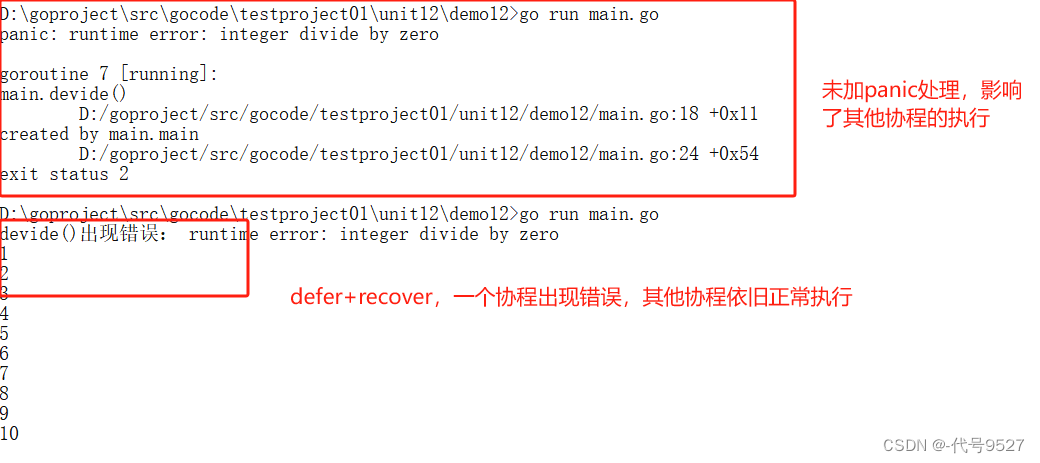
【Go】十七、进程、线程、协程
文章目录 1、进程、线程2、协程3、主死从随4、启动多个协程5、使用WaitGroup控制协程退出6、多协程操作同一个数据7、互斥锁8、读写锁9、deferrecover优化多协程 1、进程、线程 进程作为资源分配的单位,在内存中会为每个进程分配不同的内存区域 一个进程下面有多个…...
)
深入剖析JavaScript中的this(上)
在Javascript中,this 关键字是一个非常重要的概念,this这个关键字可以说是很常见也用的很多,说它简单也很简单,说它难也很难。我们经常会用到this,也经常会因为this头疼,是一个经常被误解和误用的概念&…...
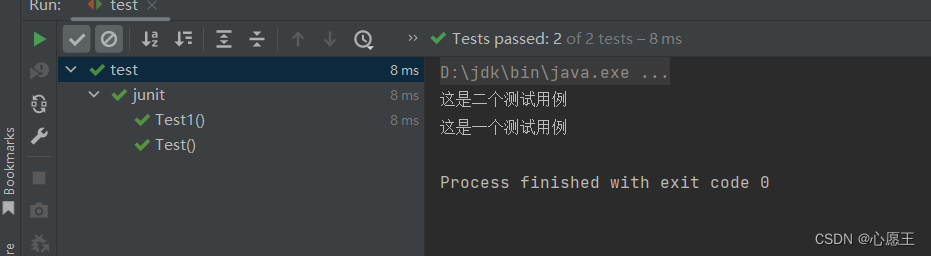
Junit深入讲解(JAVA单元测试框架)
1、此处用的是Junit5,此处pom文件需要引的依赖是 <dependency><groupId>org.junit.jupiter</groupId><artifactId>junit-jupiter-api</artifactId><version>5.9.1</version><scope>test</scope></depende…...

Spring boot如何执行单元测试?
Spring Boot 提供了丰富的测试功能,主要由以下两个模块组成: spring-boot-test:提供测试核心功能。spring-boot-test-autoconfigure:提供对测试的自动配置。 Spring Boot 提供了一个 spring-boot-starter-test一站式启动器&…...
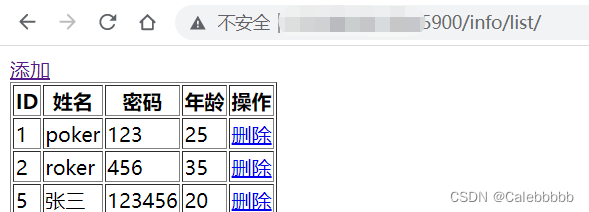
Django详细教程(一) - 基本操作
文章目录 前言一、安装Django二、创建项目1.终端创建项目2.Pycharm创建项目(专业版才可以)3.默认文件介绍 三、创建app1.app介绍2.默认文件介绍 四、快速上手1.写一个网页步骤1:注册app 【settings.py】步骤2:编写URL和视图函数对…...
Qt编译QScintilla(C++版)过程记录,报错-lqscintilla2_qt5d、libqscintilla2_qt5找不到问题解决
Qt编译QScintilla [C版] 过程记录 本文是编译该 QScintilla 组件库供 QtCreater 开发 C 桌面软件 流程记录一、编译环境 系统: Windows 10Qt:Qt 5.14.2编译套件:MinGW 64Qscintilla:QScintilla_src-2.11.6 二、下载链接 网站链…...

android QtScrcpy 共享屏幕 获取本地Address
android QtScrcpy https://gitee.com/B arryda/QtScrcpy scrcpy - 手机无线投屏到电脑 https://zhuanlan.zhihu.com/p/80264357?utm_sourcewechat_session public String getLocalIpAddress() { String ipv4; List<NetworkInterface> nilist …...

【SQL Server】1. 认识+使用
1. 创建数据库的默认存储路径 C:\ProgramData\Microsoft\Windows\Start Menu\Programs\Microsoft SQL Server 2008 R2 当我们选择删除数据库时,对应路径下的文件也就删除了 2. 导入导出数据工具的路径 3. 注册数据库遇到的问题 ??? 目前的问题就是服务器新建…...
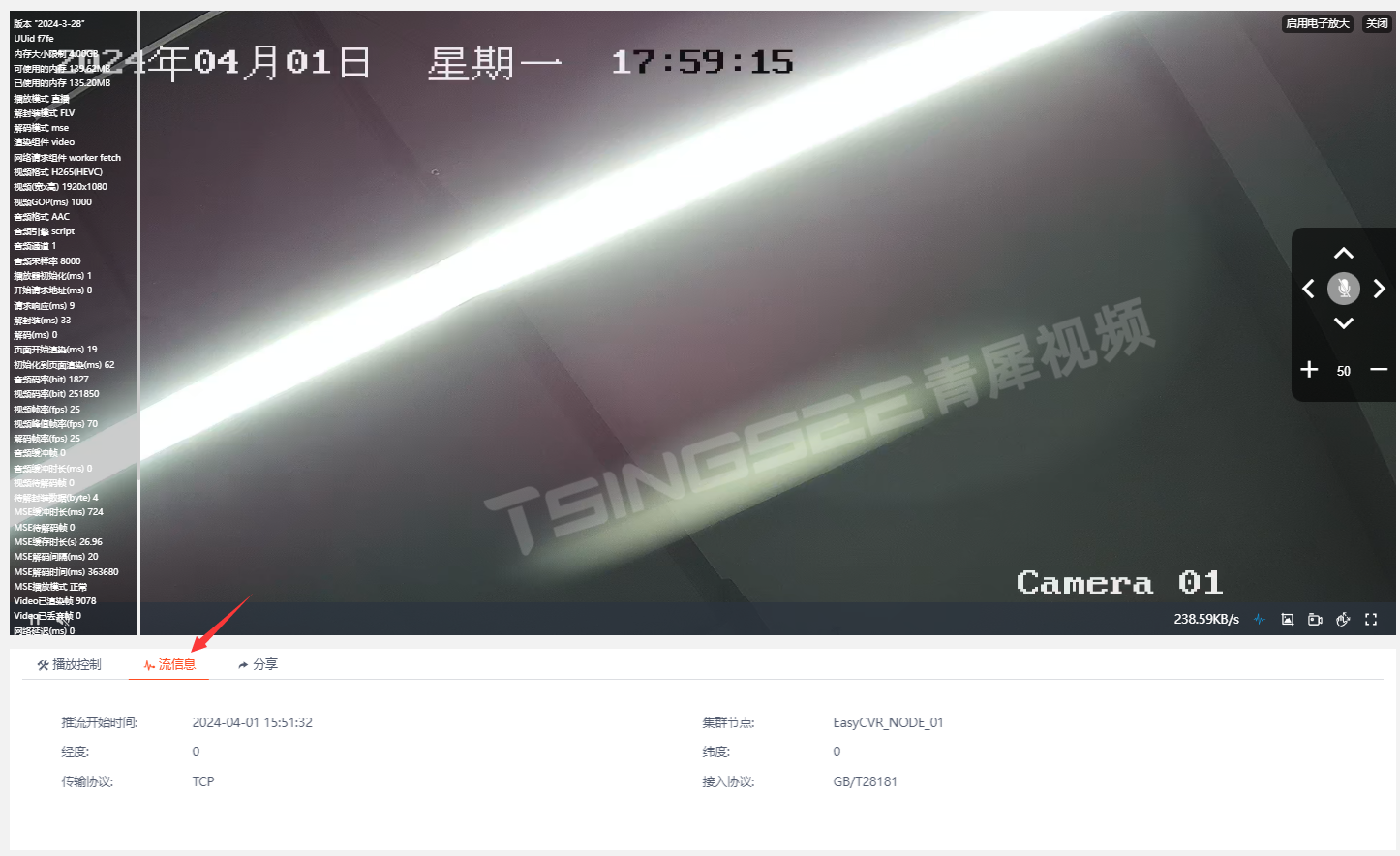
视频汇聚/安防监控/视频存储EasyCVR平台EasyPlayer播放器更新:新增【性能面板】
视频汇聚/安防监控/视频存储平台EasyCVR基于云边端架构,可以在复杂的网络环境中快速、灵活部署,平台视频能力丰富,可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级联、磁盘阵列存储、视频集中存储、云…...

图神经网络实战(7)——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图神经网络实战(7)——图卷积网络详解与实现 0. 前言1. 图卷积层2. 比较 GCN 和 GNN2.1 数据集分析2.2 实现 GCN 架构 小结系列链接 0. 前言 图卷积网络 (Graph Convolutional Network, GCN) 架构由 Kipf 和 Welling 于 2017 年提出,其理念是…...

大话设计模式之外观模式
外观模式(Facade Pattern)是一种软件设计模式,旨在提供一个简单的接口,隐藏系统复杂性,使得客户端能够更容易地使用系统。这种模式属于结构型模式,它通过为多个子系统提供一个统一的接口,简化了…...
CAD Plant3D 2024 下载地址及安装教程
CAD Plant3D是一款专业的三维工厂设计软件,用于在工业设备和管道设计领域进行建模和绘图。它是Autodesk公司旗下的AutoCAD系列产品之一,专门针对工艺、石油、化工、电力等行业的设计和工程项目。 CAD Plant3D提供了一套丰富的工具和功能,帮助…...
Intellij IDEA / Android studio 可持续开发笔记
Intellij 的Java/安卓工具链有着一种不可持续性,这种不可持续性体现在多个方面。 首先是不可持续运行。IDEA 使用时间越长,内存占用越大,从不主动释放。运行时间越长,日志越多,从不主动清理。 然后是不完整的开源&am…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
