逻辑回归(Logistic Regression)详解
逻辑回归是一种用于解决二分类问题的统计方法,它通过构建一个模型来预测某个事件的概率。
以下是逻辑回归的一些关键要点:
- 适用场景:逻辑回归特别适合于处理二分类问题,即两个类别的分类问题,例如判断一封邮件是否为垃圾邮件、一个病人是否患有某种疾病等。
- 原理概述:尽管称为回归,逻辑回归实际上是一种分类算法。它建立在线性回归的基础上,通过引入sigmoid函数(逻辑函数),将线性回归的结果映射到0和1之间,从而得到属于某一类别的概率。
- 数学模型:在逻辑回归中,通常使用最大似然估计法来估计模型参数。该方法旨在找到一组参数,使得观测数据出现的概率(也称为似然)最大化。代价函数通常采用交叉熵损失函数来衡量模型预测与实际标签之间的差异。
- 求解过程:模型的训练涉及最优化问题,目标是找到最优的模型参数,使得代价函数最小化。这通常通过梯度下降或其他优化算法实现。
- 特点优势:逻辑回归具有输出值在0和1之间、模型结果易于解释、计算效率高且可并行化等优点,因此在工业界得到了广泛的应用。
- 应用场景:逻辑回归可用于信用评分、疾病诊断、客户流失预测、市场营销响应分析等多种领域。
- 模型评估:为了评估逻辑回归模型的性能,通常会使用准确率、召回率、ROC曲线、AUC值等指标。
- 扩展应用:虽然逻辑回归主要用于二分类问题,但通过一定的技巧,如使用OVR(One-vs-Rest)策略,也可以应用于多分类问题。
- 软件工具:多数机器学习库,如Scikit-learn、TensorFlow和PyTorch等,都提供了逻辑回归的实现,方便研究者和工程师使用。
综上所述,逻辑回归以其简单性和实用性,在处理分类问题时是一个非常重要的工具。了解其原理和应用可以帮助我们更好地在实际问题中进行模型选择和调优。
相关文章:
详解)
逻辑回归(Logistic Regression)详解
逻辑回归是一种用于解决二分类问题的统计方法,它通过构建一个模型来预测某个事件的概率。 以下是逻辑回归的一些关键要点: 适用场景:逻辑回归特别适合于处理二分类问题,即两个类别的分类问题,例如判断一封邮件是否为…...

.vimrc文件的语句语法
本文结构: a、简介 b、详细解释其中的一些常见语句和语法。 a、.vimrc 文件是 Vim 编辑器用于配置用户设置和自定义行为的文件。当 Vim 启动时,它会读取 .vimrc 文件中的命令和设置,并根据这些指令来配置编辑器的行为。 b、.vimrc 文件中…...

c语言之函数指针作形参
在一些c语言的大工程中,会在定义的函数中,把一些其他函数指针作为本函数形参。 函数指针作形参的例子 代码如下: #include<stdio.h> int max(int a,int b) { return(a>b?a:b); } int min(int a,int b) { return(a<b?a:b); } i…...

python文件的读取操作
打开文件 fopen("F:/python/helloworld/测试.txt","r",encoding"UTF-8")读取文件 print(f"读取10个字节的结果{f.read(10)}") print(f"读取全部字节的结果{f.read()}") linesf.readlines() print(f"{lines}")读…...

查看并设定【网络适配器】的优先级(跃点数)
目录 前言: 1.查看所有的适配器 2.修改优先级(需要以管理员身份运行) 跃点数(InterfaceMetric ) DHCP 3.修改后的效果 pwoerShell 再次运行之前的程序 4.其他 参考 网络适配器1,8相关知识介绍1 …...
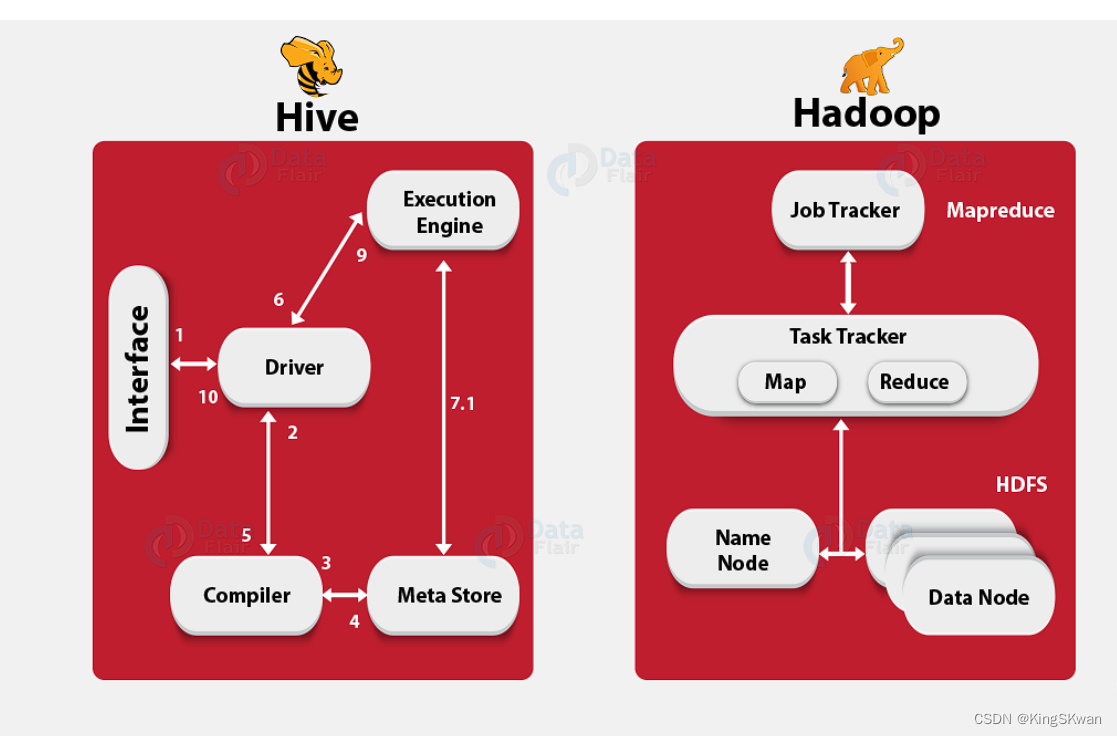
深入理解 Hadoop 上的 Hive 查询执行流程
在 Hadoop 生态系统中,Hive 是一个重要的分支,它构建在 Hadoop 之上,提供了一个开源的数据仓库系统。它的主要功能是查询和分析存储在 Hadoop 文件中的大型数据集,包括结构化和半结构化数据。Hive 在数据查询、分析和汇总方面发挥…...

JS封装网页进入/退出全屏功能,兼容各大主流浏览器
1、演示 2、封装进入全屏函数 mozRequestFullScreen:兼容Firefox webkitRequestFullscreen:兼容 Chrome、Safari、Opera msRequestFullscreen:兼容:IE/Edge const enter () > {const element document.documentElementif (el…...

el-table的复选框勾选整行变色
要实现el-table的复选框勾选整行变色,你可以使用element-ui提供的row-class-name属性结合scoped slot来完成。 首先,你需要为el-table组件添加 row-class-name 属性,并给它绑定一个方法。在这个方法中,你可以根据你的业务逻辑来判…...

一步一步写线程之八线程池的完善之二数据结构封装
一、数据容器 在前面分析过,不管是线程任务的封装还是同步数据队列的封装,都是需要一个数据结构的。一用来说,如果没有什么特殊的原因,开发者都是使用STL中数据结构。比如前面经常见到的std::queue,std::deque,std::vector,std::…...

go连接数据库(原生)
根据官网文档 Go Wiki: SQL Database Drivers - The Go Programming Language 可以看到go可以连接的关系型数据库 常用的关系型数据库基本上都支持,下面以mysql为例 下载mysql驱动 打开上面的mysql链接 GitHub - go-sql-driver/mysql: Go MySQL Driver i…...
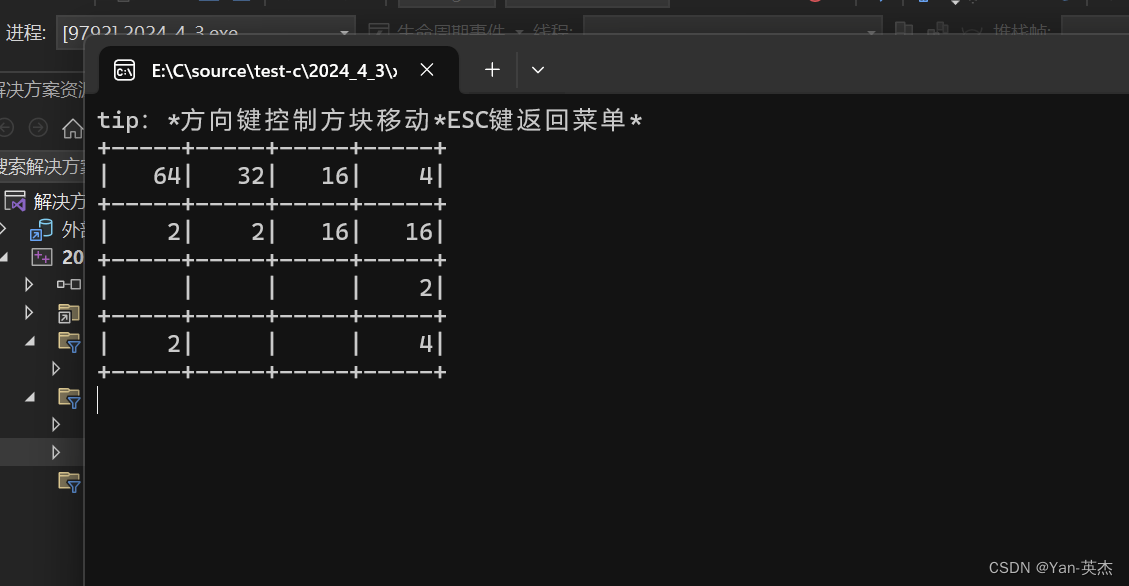
【C语言】2048小游戏【附源码】
欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 一、游戏描述: 2048是一款数字益智类游戏,玩家需要使用键盘控制数字方块的移动,合并相同数字的方块,最终达到数字方块上出现“2048”的目标。 每次移动操作,所…...
部署项目遇到的各种问题总结
文章目录 前言一、后端问题 jar包运行出现错误宝塔面板使用jdk17二、数据库问题 版本问题三、前端问题 连不上后端总结 前言 在做完项目之后,为了让别人访问到自己的网站,就需要部署前端后端以及数据库,但是在部署的过程中出现了各种问题和困…...
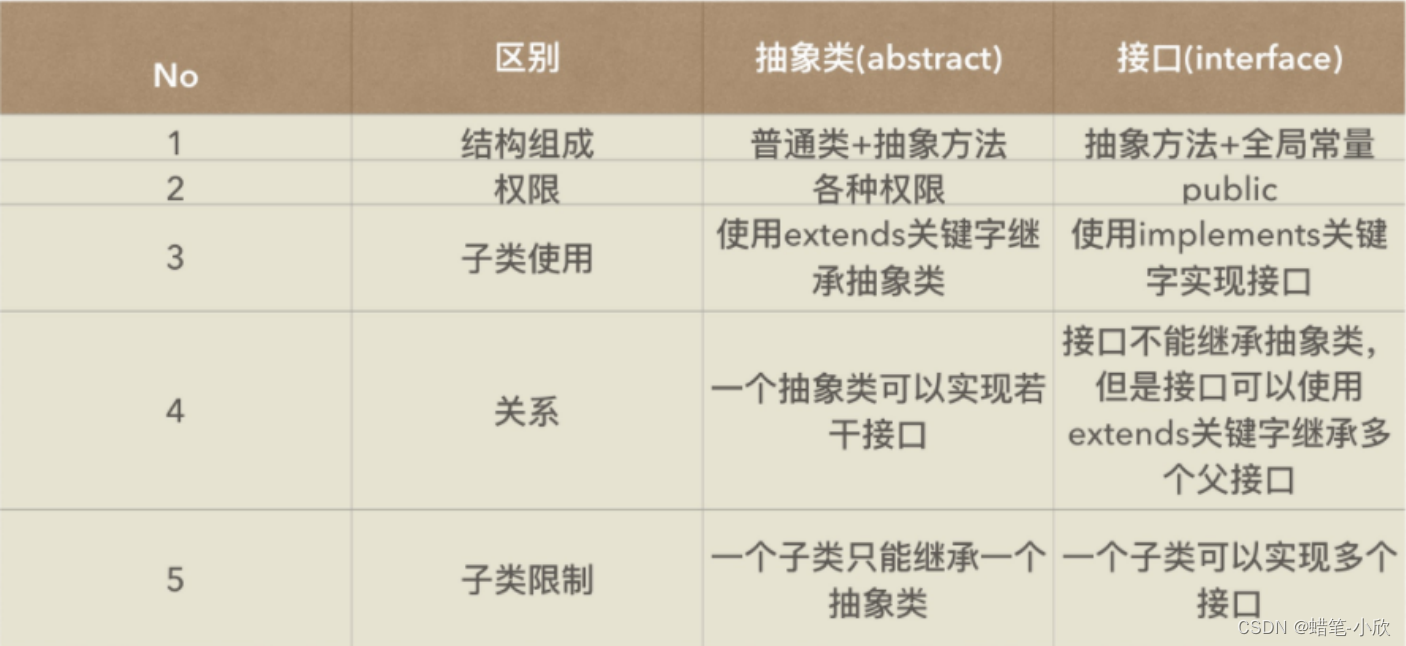
JavaSE:抽象类和接口
目录 一、前言 二、抽象类 (一)抽象类概念 (二)使用抽象类的注意事项 (三)抽象类的作用 三、接口 (一)接口概念 (二)接口语法规则 (三&a…...

发票是扫码验真好,还是OCR后进行验真好?
随着科技的进步,电子发票的普及使得发票的验真方式也在不断演进。目前,我们常见的发票验真方式主要有两种:一种是扫描发票上的二维码进行验真,另一种是通过OCR(Optical Character Recognition,光学字符识别…...

【AIGC调研系列】AIGC+Jmeter实现接口自动化测试脚本生成
AIGC(人工智能生成内容)结合JMeter实现接口自动化测试脚本生成的方法,主要涉及到通过流量收集工具和AIGC技术获取用户操作接口数据,并利用这些数据生成自动化测试脚本的过程。这种方法可以有效提高软件测试的效率和质量[1]。JMete…...

前端|babel升级
问题 项目不支持可选链调用过多的 babel 插件 步骤 基础包 dependencies “react-scripts”: “5.0.1” devDependencies “customize-cra”: “^1.0.0”,“react-app-rewired”: “^2.2.1”, 框架包 dependencies “react”: “16.13.1”,“react-dom”: “16.13.1”, …...

【微服务】spring状态机模式使用详解
一、前言 在很多系统中,通常会涉及到某个业务需要进行各种状态的切换操作,例如在审批流程场景下,某个审批的向下流转需要依赖于上一个状态的结束,再比如电商购物场景中,一个订单的生命周期往往伴随着不同的状态&#…...
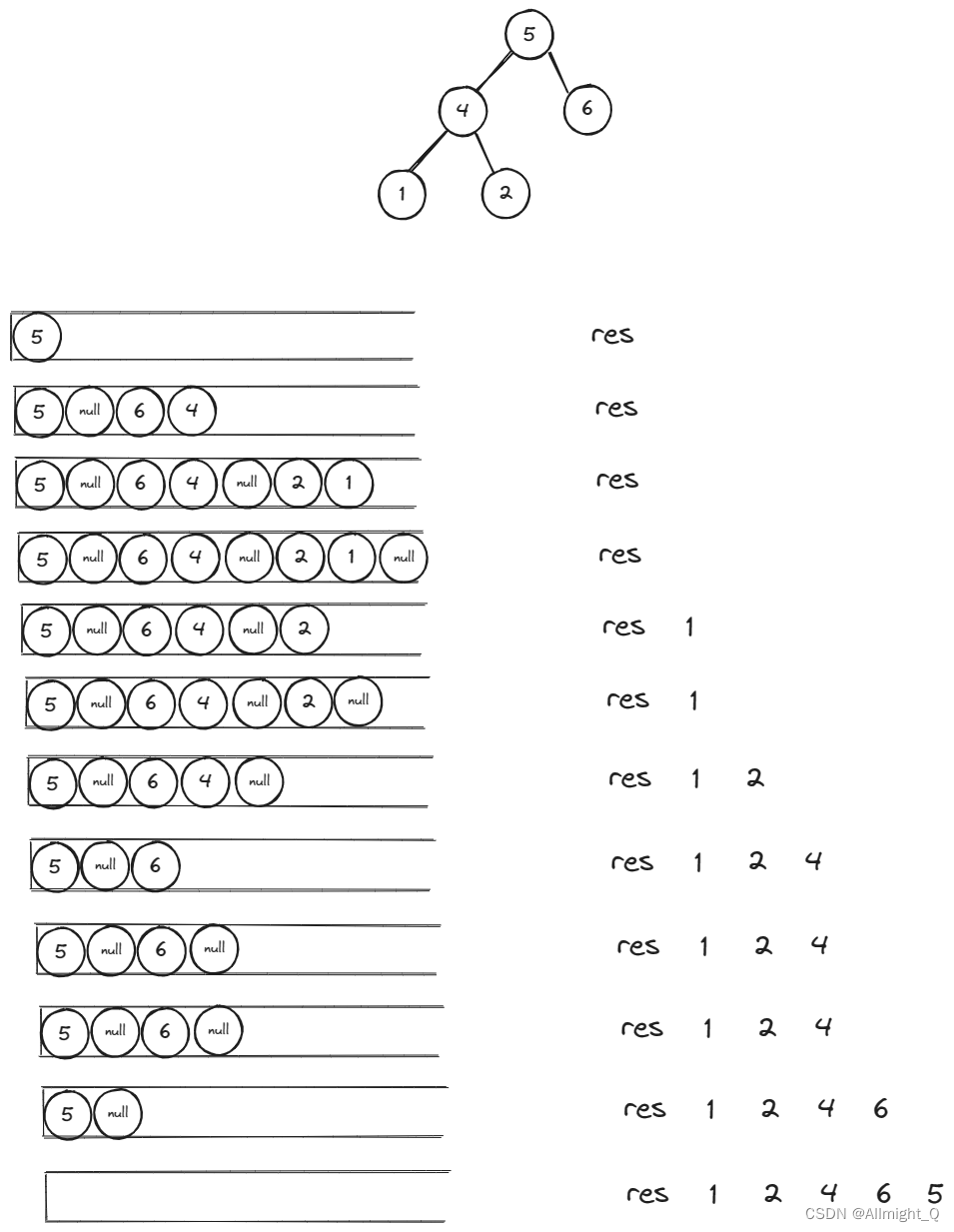
【算法刷题day14】Leetcode:144.二叉树的前序遍历、94.二叉树的中序遍历、145.二叉树的后序遍历
文章目录 二叉树递归遍历解题思路代码总结 二叉树的迭代遍历解题思路代码总结 二叉树的统一迭代法解题思路代码总结 草稿图网站 java的Deque 二叉树递归遍历 题目: 144.二叉树的前序遍历 94.二叉树的中序遍历 145.二叉树的后序遍历 解析:代码随想录解析…...

mysql闲谈
如何定位慢查询 1、测试环境压测时,有的接口非常慢,响应时间超过2秒以上。当时系统部署了运维的监控系统Skywalking,在展示报表中可以看到是哪儿个接口慢,可以看到SQL具体执行时间。 2、如果没有类似的监控系统,在Mysq…...
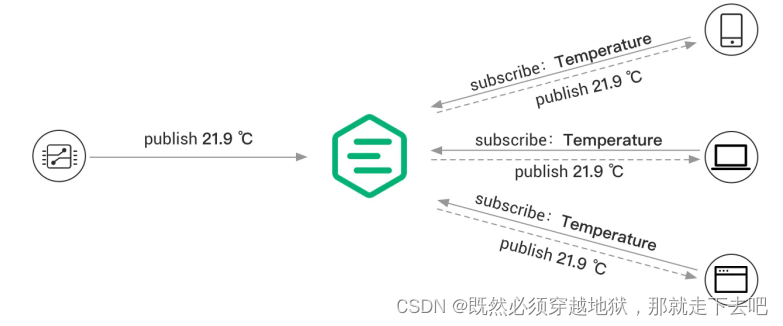
物联网学习1、什么是 MQTT?
MQTT(Message Queuing Telemetry Transport)是一种轻量级、基于发布-订阅模式的消息传输协议,适用于资源受限的设备和低带宽、高延迟或不稳定的网络环境。它在物联网应用中广受欢迎,能够实现传感器、执行器和其它设备之间的高效通…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
