算法学习——LeetCode力扣图论篇1(797. 所有可能的路径、200. 岛屿数量、695. 岛屿的最大面积)
算法学习——LeetCode力扣图论篇1

797. 所有可能的路径
797. 所有可能的路径 - 力扣(LeetCode)
描述
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
示例
示例 1:
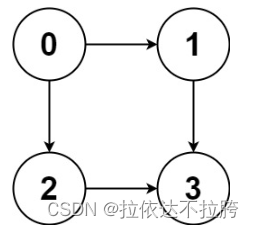
输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
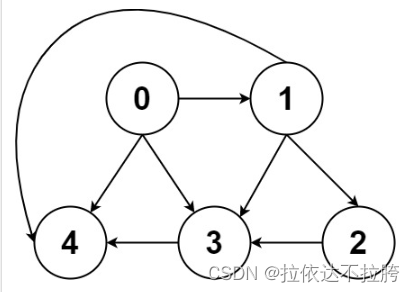
输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
提示
n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i(即不存在自环)
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图(DAG)
代码解析
class Solution {
public:vector<vector<int>> result;vector<int> path;void dfs(vector<vector<int>>& graph , int indnx){if(indnx == graph.size()-1) {path.push_back(graph.size()-1);result.push_back(path);path.pop_back();return;}for(int i=0 ; i<graph[indnx].size() ;i++){path.push_back(indnx);dfs(graph,graph[indnx][i]);path.pop_back();}return;}vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {dfs(graph,0);return result;}
};
200. 岛屿数量
200. 岛屿数量 - 力扣(LeetCode)
描述
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
提示
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’
代码解析
深度优先搜索dfs
class Solution {
public:int result = 0;int m =0 ,n=0;int dir[4][2] = {0,1, 0,-1 , -1,0 , 1,0};void dfs(vector<vector<char>>& grid , vector<vector<bool>> &path , int x , int y){for(int i=0 ; i<4 ;i++){int next_x = x + dir[i][0];int next_y = y + dir[i][1];if(next_x<0||next_x>=m||next_y<0||next_y>=n) continue;else if( path[next_x][next_y] == false && grid[next_x][next_y] == '1') { path[next_x][next_y] = true;dfs(grid,path,next_x,next_y);}}return;}int numIslands(vector<vector<char>>& grid) {m = grid.size();n = grid[0].size();vector<vector<bool>> path( m , vector<bool>( n ,false) );for(int i=0 ; i<m ;i++){for(int j=0 ; j<n ;j++){if(path[i][j] == false && grid[i][j] == '1'){result++;path[i][j] = true;dfs(grid,path,i,j);}}}return result;}
};
广度优先搜索bfs
class Solution {
public:int result = 0;int m =0 ,n=0;int dir[4][2] = {0,1, 0,-1 , -1,0 , 1,0};void bfs(vector<vector<char>>& grid , vector<vector<bool>> &path , int x , int y){queue<pair<int,int>> my_que;my_que.push({x,y});path[x][y] = true;while(my_que.size() != 0){pair<int,int> cur = my_que.front();my_que.pop();for(int i=0 ; i<4 ;i++){int next_x = cur.first + dir[i][0];int next_y = cur.second + dir[i][1];if(next_x<0||next_x>=m||next_y<0||next_y>=n) continue;else if( path[next_x][next_y] == false && grid[next_x][next_y] == '1') { my_que.push({next_x,next_y});path[next_x][next_y] = true;}}}return;}int numIslands(vector<vector<char>>& grid) {m = grid.size();n = grid[0].size();vector<vector<bool>> path( m , vector<bool>( n ,false) );for(int i=0 ; i<m ;i++){for(int j=0 ; j<n ;j++){if(path[i][j] == false && grid[i][j] == '1'){result++;path[i][j] = true;bfs(grid,path,i,j);}}}return result;}
};
695. 岛屿的最大面积
695. 岛屿的最大面积 - 力扣(LeetCode)
描述
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例
示例 1:
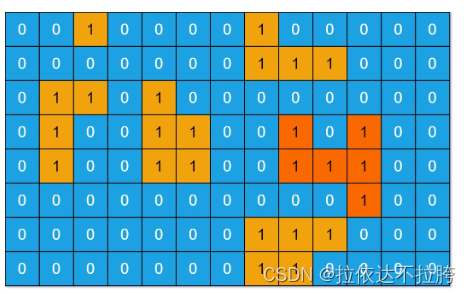
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
提示
m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1
代码解析
class Solution {
public:int dir[4][2] = {0,1,0,-1,-1,0,1,0};int m=0,n=0;int result = 0;int tmp_result = 0;void dfs(vector<vector<int>>& grid , vector<vector<bool>> &path , int x ,int y){for(int i=0 ; i<4 ;i++){int next_x = x + dir[i][0];int next_y = y + dir[i][1];if(next_x<0 || next_x>=m || next_y<0 || next_y>=n) continue;if(grid[next_x][next_y] == 1 && path[next_x][next_y] == false){tmp_result++;path[next_x][next_y] = true;dfs(grid,path,next_x,next_y);}}}int maxAreaOfIsland(vector<vector<int>>& grid) {m = grid.size();n = grid[0].size();vector<vector<bool>> path(m , vector<bool>( n , false ));for(int i=0 ; i<m ;i++){for(int j=0 ; j<n ;j++){if(grid[i][j] == 1 && path[i][j] == false){path[i][j] = true;tmp_result = 1;dfs(grid,path,i,j);if(tmp_result > result) result =tmp_result;}}}return result;}
};
相关文章:

算法学习——LeetCode力扣图论篇1(797. 所有可能的路径、200. 岛屿数量、695. 岛屿的最大面积)
算法学习——LeetCode力扣图论篇1 797. 所有可能的路径 797. 所有可能的路径 - 力扣(LeetCode) 描述 给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特…...

【IP组播】PIM-SM的RP、RPF校验
目录 一:PIM-SM的RP 原理概述 实验目的 实验内容 实验拓扑 1.基本配置 2.配置IGP 3.配置PIM-SM和静态RP 4.配置动态RP 5.配置Anycast RP 二: RPF校验 原理概述 实验目的 实验内容 实验拓扑 1.基本配置 2.配置IGP 3.配置PIM-DM 4.RPF校…...

前端代码规范-命名规范
命名规则 camelCase(小驼峰式命名法 —— 首字母小写)PascalCase(大驼峰式命名法 —— 首字母大写)kebab-case(短横线连接式)Snake(下划线连接式) 项目名称 项目名 全部采用小写方…...

移动端APP测试常见面试题精析
现在面试测试职位,要求非常全面,那么APP测试一般需要哪些技术呢?下面总结了APP测试常见面试题: 1.Android四大组件? Activity:描述UI,并且处理用户与机器屏幕的交互。应用程序中,一个Activity就相当于手…...
报错[Vue warn]: $listeners is readonly. $attrs is readonly.怎么解决?
代码也没有逻辑错误,但是报错 [Vue warn]: $listeners is readonly. $attrs is readonly. 情况1:多处声明了new Vue,解决方案:删除一个,用全局变量引用同一个Vue 情况2:import Vue from Vue;第二个Vue首字…...
apexd bootstrap)
android 14 apexd分析(1)apexd bootstrap
Apex的由来,我们都知道普通的apk我们可以通过应用商店playstore等进行更新,apex的引入是google希望也能通过playstore更新bin文件.so etc配置文件等类型文件. 这些文件的安装实际通过apexd来进行,现在我们来解析一下apexd, apexd的启动分为两个阶段,bootstrap和普通apexd启…...

C++ 中的 vector 的模拟实现【代码纯享】
文章目录 C 中的 vector 模拟实现1. vector 的基本概念2. vector 的基本操作3. vector 的模拟实现4.代码纯享5. 总结 C 中的 vector 模拟实现 在 C 中,vector 是一个非常重要的容器,它提供了动态数组的功能。在本篇博客中,我们将尝试模拟实现…...
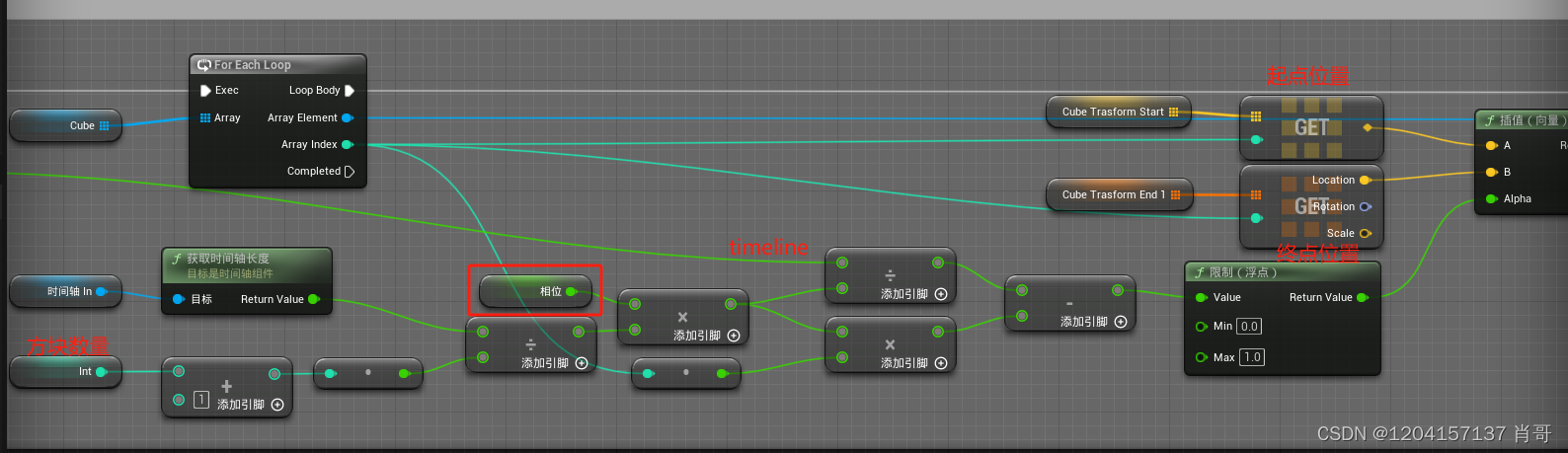
UE4 方块排序动画
【动画效果】 入动画: 出动画: 【分析】 入动画:方块动画排序方式为Z字形,堆砌方向为X和Y轴向 出动画:方块动画排序方式为随机 【关键蓝图】 1.构建方块砌体 2.入/出动画...
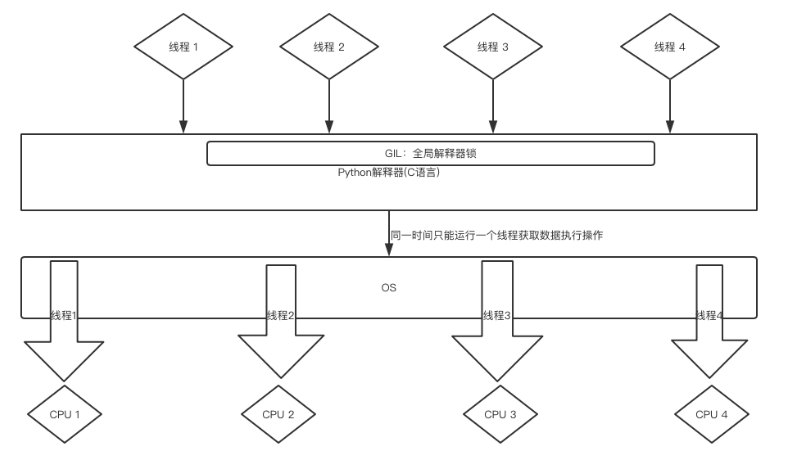
网络与并发编程(一)
并发编程介绍_串行_并行_并发的区别 串行、并行与并发的区别 串行(serial):一个CPU上,按顺序完成多个任务并行(parallelism):指的是任务数小于等于cpu核数,即任务真的是一起执行的并发(concurrency):一个CPU采用时间…...

超详细工具Navicat安装教程
Navicat是一款功能强大的数据库管理工具,可用于管理多种类型的数据库,包括MySQL、MariaDB、SQL Server、SQLite、Oracle和PostgreSQL等。以下是Navicat工具的一些主要特点和功能: 一.功能介绍 跨平台支持 多种数据库支持 直观的用户界面 数据…...
RN在android/ios手机剪切图片的操作
之前写过一个React Native调用摄像头画面及拍照和保存图片到相册全流程但是这个仅限于调用摄像头拍照并保存图片,今天再写一个版本的操作,这个博客目前实现的有三点操作: 调用摄像头拍照对照片进行剪切从相册选取图片 功能上面来说有两点: 点击按钮可以对摄像头进行拍照,拍完照…...

C语言 | Leetcode C语言题解之第6题Z字形变换
题目: 题解: char * convert(char * s, int numRows){int n strlen(s), r numRows;if (r 1 || r > n) {return s;}int t r * 2 - 2;char * ans (char *)malloc(sizeof(char) * (n 1));int pos 0;for (int i 0; i < r; i) { // 枚举矩阵的…...

C 回调函数的两种使用方法
对回调(callback)函数的一点粗陋理解,在我小时候,隔壁村有家月饼小作坊(只在中秋那段时间手工制作一些月饼出售,后来好像不做了),做出的月饼是那种很传统很经典的款式,里…...
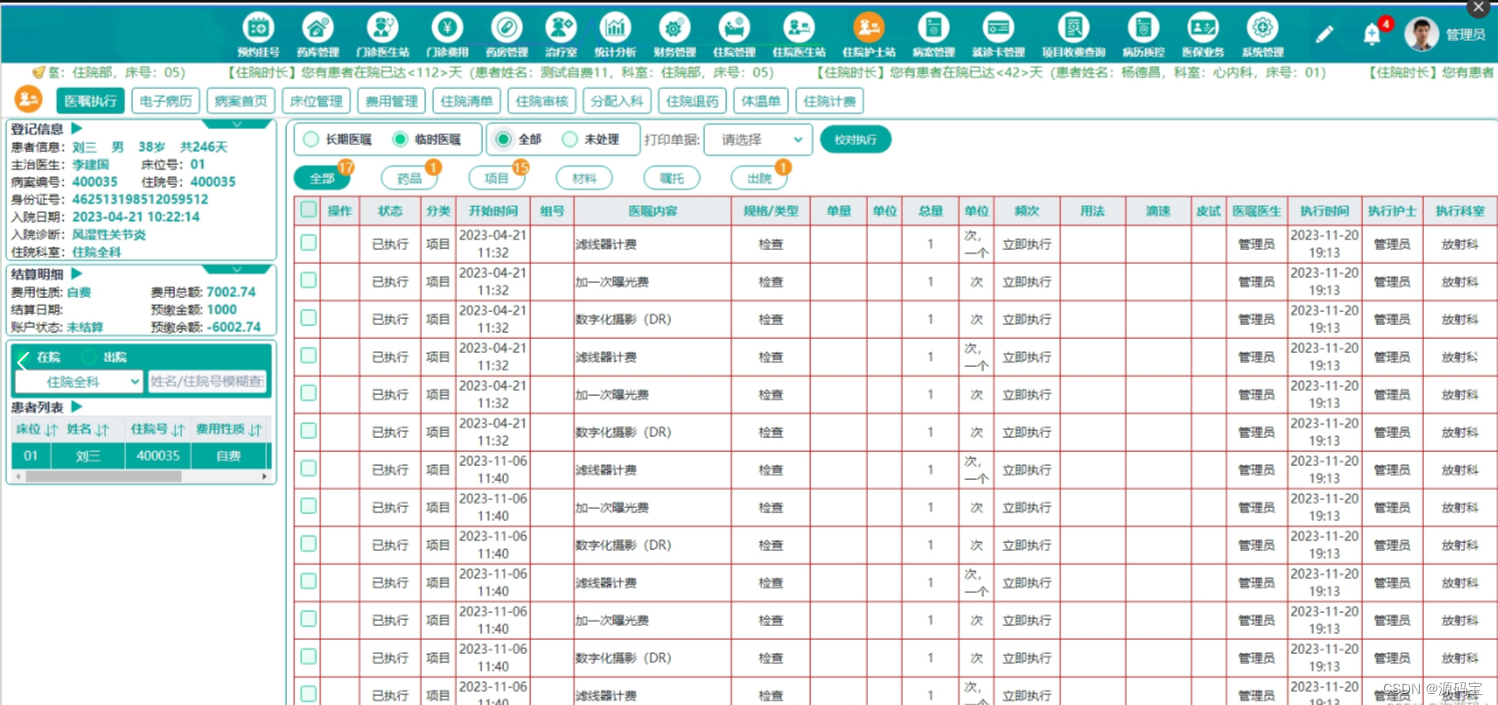
医院云HIS系统源码,二级医院、专科医院his系统源码,经扩展后能够应用于医联体/医共体
基于云计算技术的B/S架构的HIS系统,为医疗机构提供标准化的、信息化的、可共享的医疗信息管理系统,实现医患事务管理和临床诊疗管理等标准医疗管理信息系统的功能。 系统利用云计算平台的技术优势,建立统一的云HIS、云病历、云LIS࿰…...
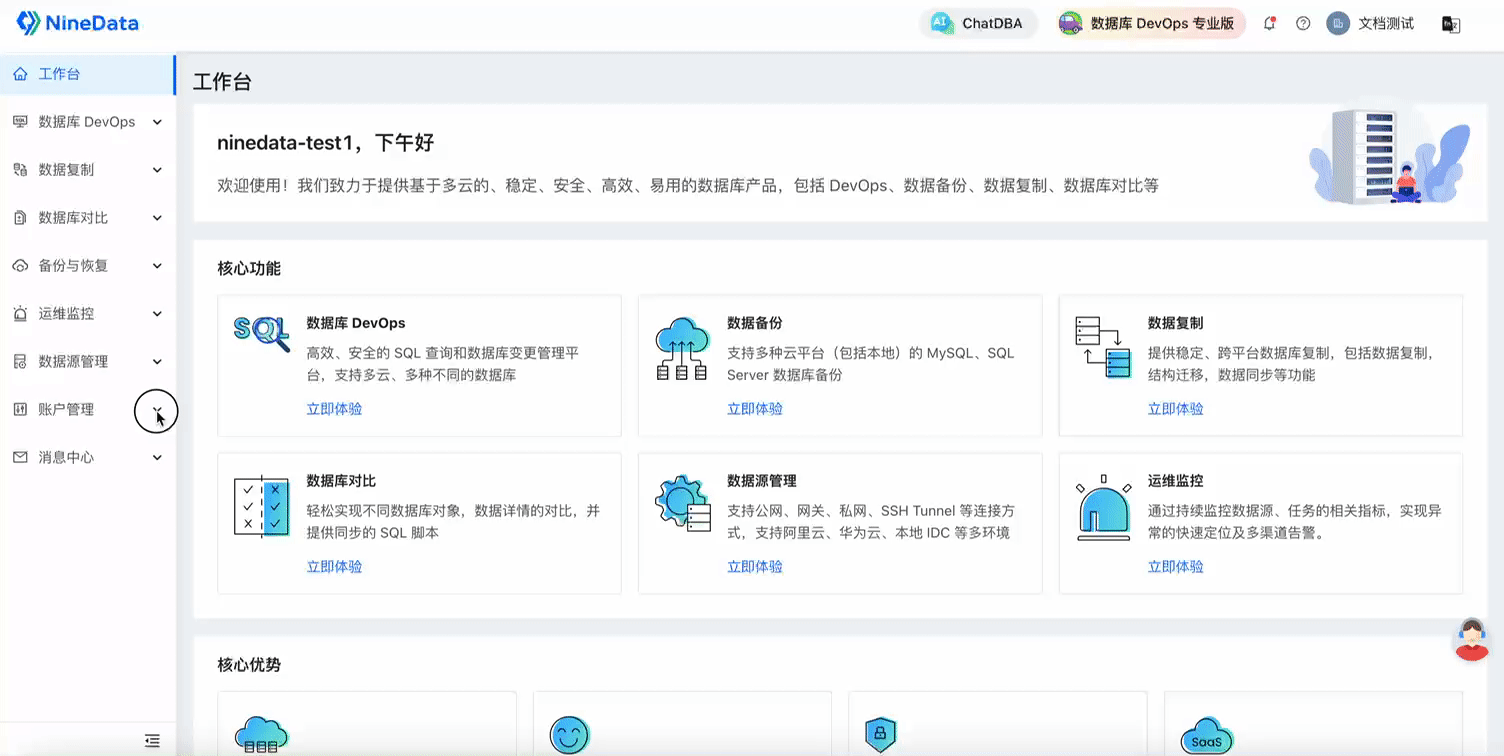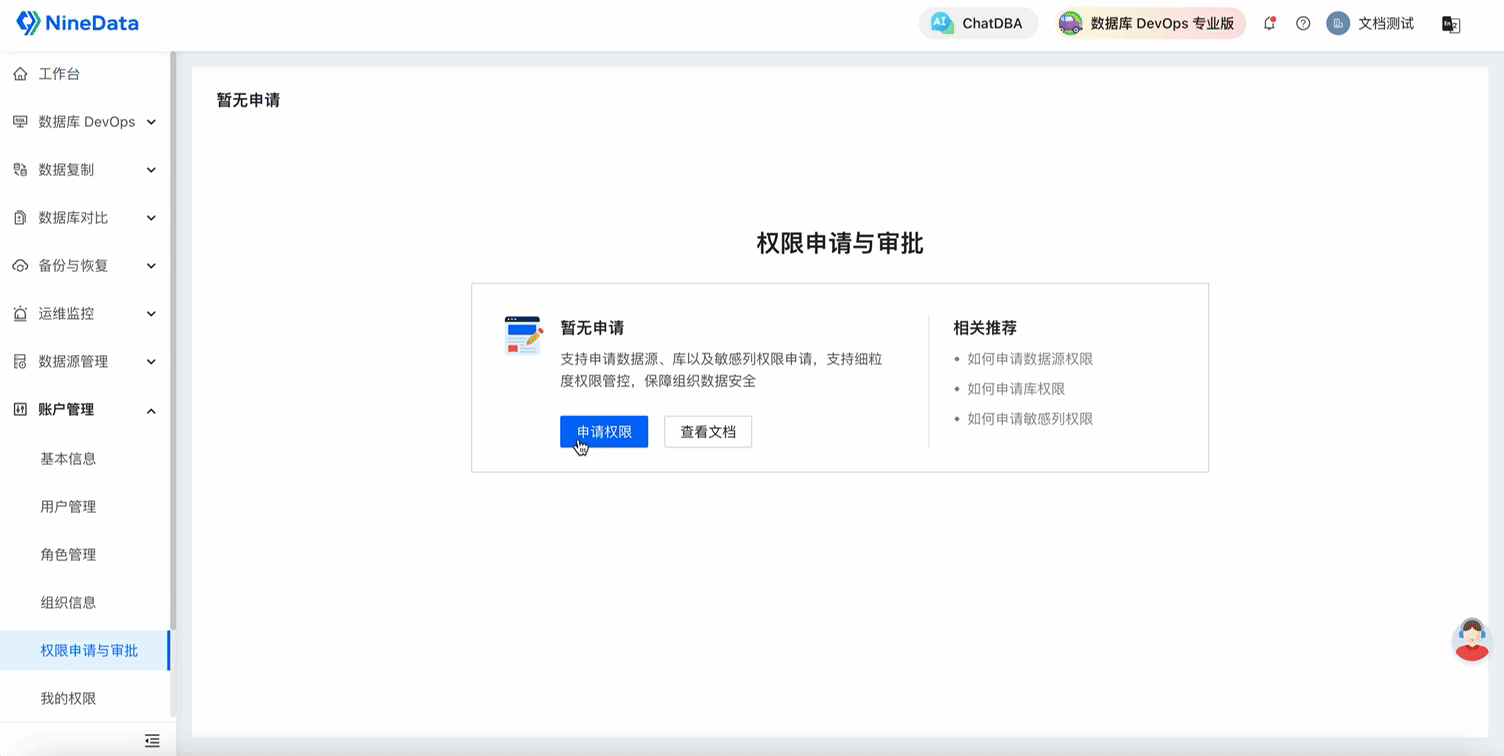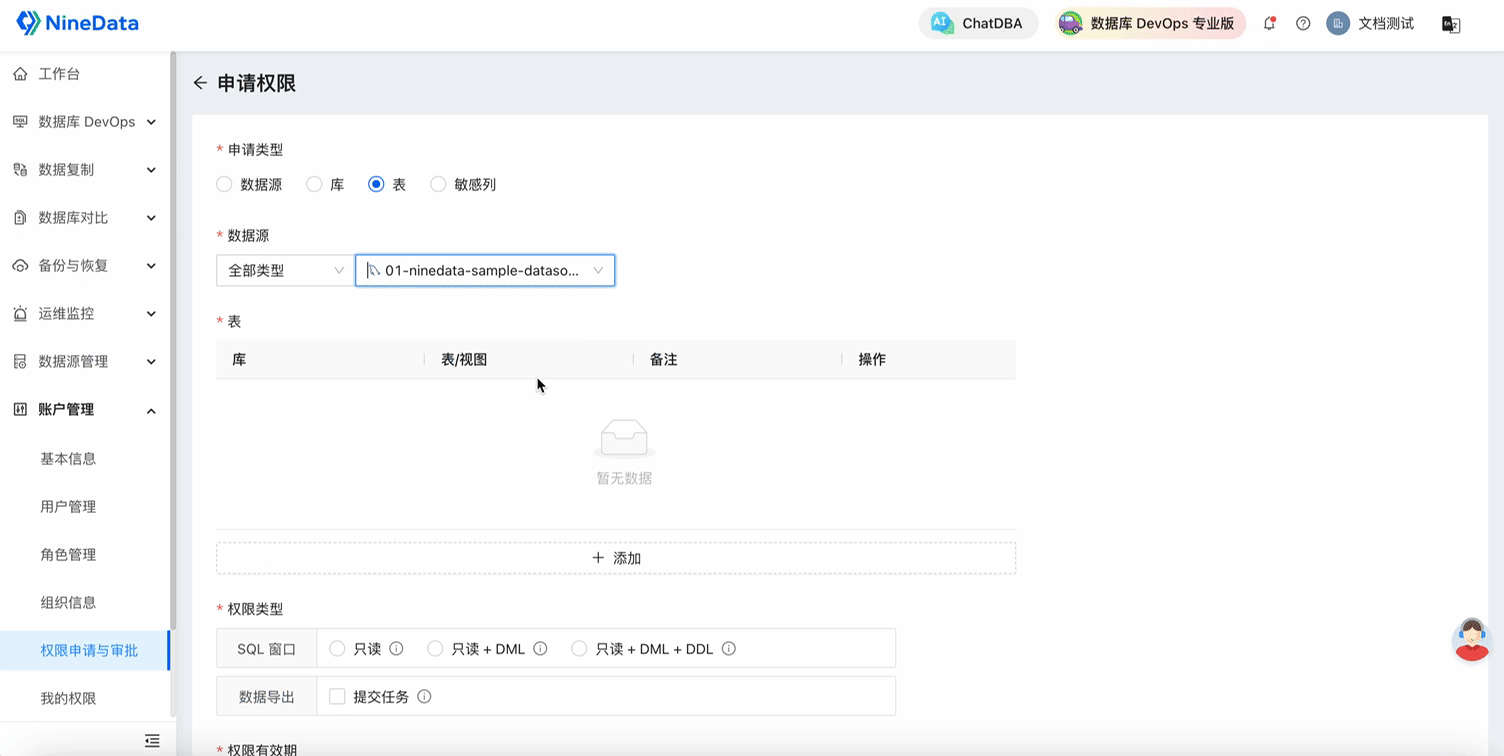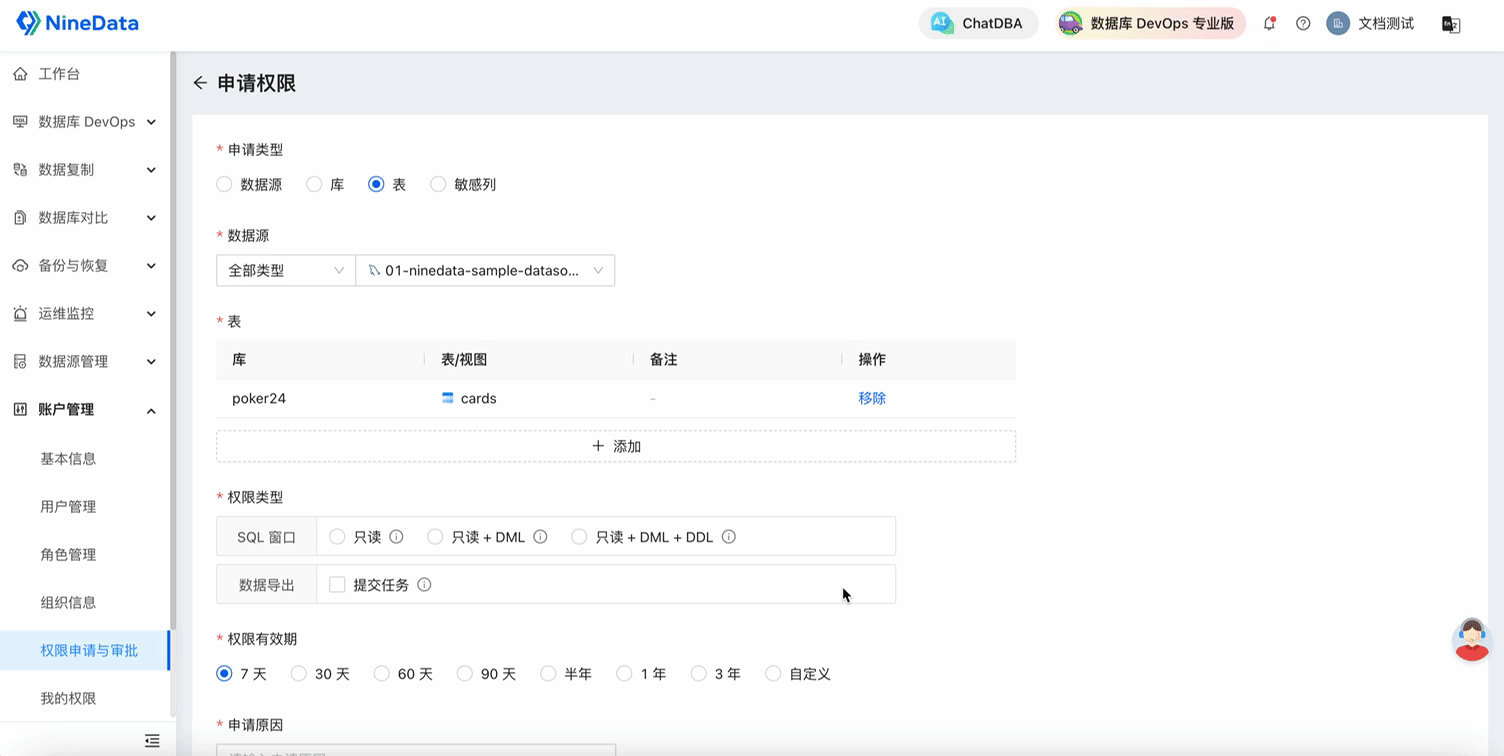
NineData云原生智能数据管理平台新功能发布|2024年3月版
数据库 DevOps - 大功能升级 SQL 开发早期主要提供 SQL 窗口(IDE)功能,在产品经过将近两年时间的打磨,新增了大量的企业级功能,已经服务了上万开发者,覆盖了数据库设计、开发、测试、变更等生命周期的功能…...
java Web 疫苗预约管理系统用eclipse定制开发mysql数据库BS模式java编程jdbc
一、源码特点 JSP 疫苗预约管理系统是一套完善的web设计系统,对理解JSP java 编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,eclipse开发,数据库为Mysql5.0,使…...

Qt5.14.2 揭秘Qt日志神器高效诊断程序潜在隐疾
对程序员而言,代码中的bug往往如同无影无踪的隐疾,影响着程序的健康运行。而及时有效的诊断手段则是治疗这些隐疾的良药。今天,我们将一窥Qt日志框架QLoggingCategory的神奇功效,探究它如何为你的Qt应用程序构筑坚实的诊断防火墙。…...

Mac上设置环境变量PATH
一、配置文件有哪些 在Mac系统中,环境变量的配置文件主要包括以下几个: 文件名称描述/etc/paths系统级别的配置文件,系统启动时会加载它。/etc/profile系统级别的配置文件,所有用户登录时都会读取该文件。~/.bash_profile用户级别…...
Redis 全景图(1)--- 关于 Redis 的6大模块
这是我第一次尝试以长文的形式写一篇 Redis 的总结文章。这篇文章我想写很久了,只是一直碍于我对 Redis 的掌握没有那么的好,因此迟迟未动笔。这几天,我一直在看各种不同类型的 Redis 文章,通过阅读这些文章,引发了我对…...

Lambda表达式,Stream流
文章目录 Lambda表达式作用前提函数式接口特点 语法省略模式和匿名对象类的区别 Stream流思想作用三类方法获取方法单列集合(Collection[List,Set双列集合Map(不能直接获取)数组同一类型元素(Stream中的静态方法) 常见的中间方法终结方法收集方法 Optional类 Lambda表达式 作用…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
