(C)1005 继续(3n+1)猜想
1005 继续(3n+1)猜想:
问题描述
卡拉兹(Callatz)猜想已经在1001中给出了描述。在这个题目里,情况稍微有些复杂。
当我们验证卡拉兹猜想的时候,为了避免重复计算,可以记录下递推过程中遇到的每一个数。例如对 n=3 进行验证的时候,我们需要计算 3、5、8、4、2、1,则当我们对 n=5、8、4、2 进行验证的时候,就可以直接判定卡拉兹猜想的真伪,而不需要重复计算,因为这 4 个数已经在验证3的时候遇到过了,我们称 5、8、4、2 是被 3“覆盖”的数。我们称一个数列中的某个数 n 为“关键数”,如果 n 不能被数列中的其他数字所覆盖。
现在给定一系列待验证的数字,我们只需要验证其中的几个关键数,就可以不必再重复验证余下的数字。你的任务就是找出这些关键数字,并按从大到小的顺序输出它们。
输入格式:
每个测试输入包含 1 个测试用例,第 1 行给出一个正整数 K (<100),第 2 行给出 K 个互不相同的待验证的正整数 n (1<n≤100)的值,数字间用空格隔开。
输出格式:
每个测试用例的输出占一行,按从大到小的顺序输出关键数字。数字间用 1 个空格隔开,但一行中最后一个数字后没有空格。
输入样例:
6
3 5 6 7 8 11
输出样例:
7 6
解决方案:
#include<stdio.h>
#include<string.h>
int main(){int n;scanf("%d",&n);int a[100],b[10000],stat[100];int j=0;int final[100],f=0;int tool,y;if(n==-1) return 0;memset(final,-1,sizeof(final));memset(b,-1,sizeof(b));memset(a,-1,sizeof(a));memset(stat,-1,sizeof(stat));//初始化为0for(int i=0;i<n;i++){scanf("%d",&a[i]);}for(int i=0;i<n;i++){stat[i]=a[i];}//输入存进数组,并复制一份 for(int i=0;i<n;i++){while(a[i]>1){if(a[i]%2!=0){a[i]=(a[i]*3+1)/2;b[j++]=a[i];} else{a[i]=a[i]/2;b[j++]=a[i];}}}//用b来存储递推过程中所有的数for(int i=0;b[i]!=-1;i++){for(int k=0;k<n;k++){if(stat[k]==b[i]){stat[k]=-1;}}}//剔除被覆盖数,剩余未被覆盖数for(int i=0;i<n;i++){if(stat[i]!=-1){final[f]=stat[i];f++;}}//将零散的未被覆盖数放于最终数组(final)for(int i=0;i<f;i++){for(int z=i+1;z<f;z++){if(final[i]<final[z]){tool=final[i];final[i]=final[z];final[z]=tool;}}}//排序for(y=0;y<f-1;y++){printf("%d ",final[y]);}printf("%d",final[y]);return 0;
}
收获:
最后一个测试点不通过是数组长度不够,
一边debug一边理思路。
相关文章:
1005 继续(3n+1)猜想)
(C)1005 继续(3n+1)猜想
1005 继续(3n1)猜想: 问题描述 卡拉兹(Callatz)猜想已经在1001中给出了描述。在这个题目里,情况稍微有些复杂。 当我们验证卡拉兹猜想的时候,为了避免重复计算,可以记录下递推过程中遇到的每一个数。例如对 n3 进行验证的时候&a…...
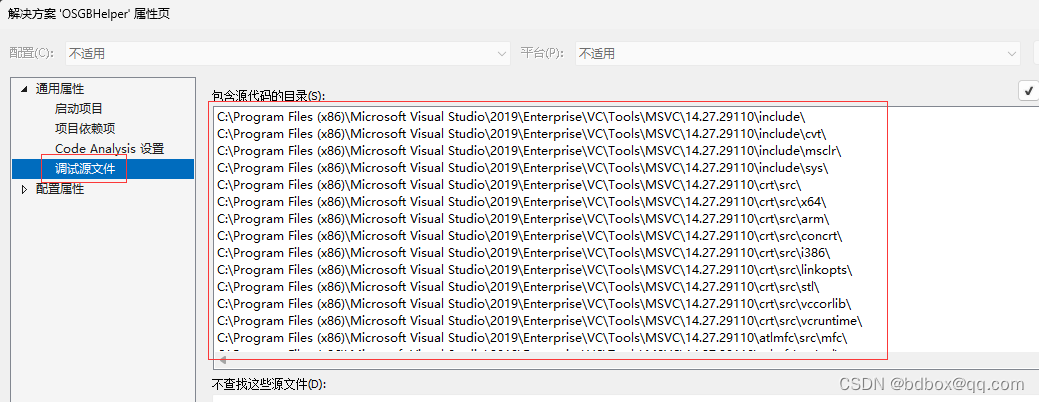
编译好的C++应用程序拷贝到其它电脑,提示dll未找到依赖项的解决方法。
编译好的C应用程序拷贝到其它电脑上,运行时出现提示dll未找到依赖项。 由于dll依赖于其它dll,在开发用电脑上的环境不能完全与其它电脑相同。 解决办法是找到调用到的dll依赖的所有dll,拷贝到运行目录下。 在开发电脑上: 1、开…...
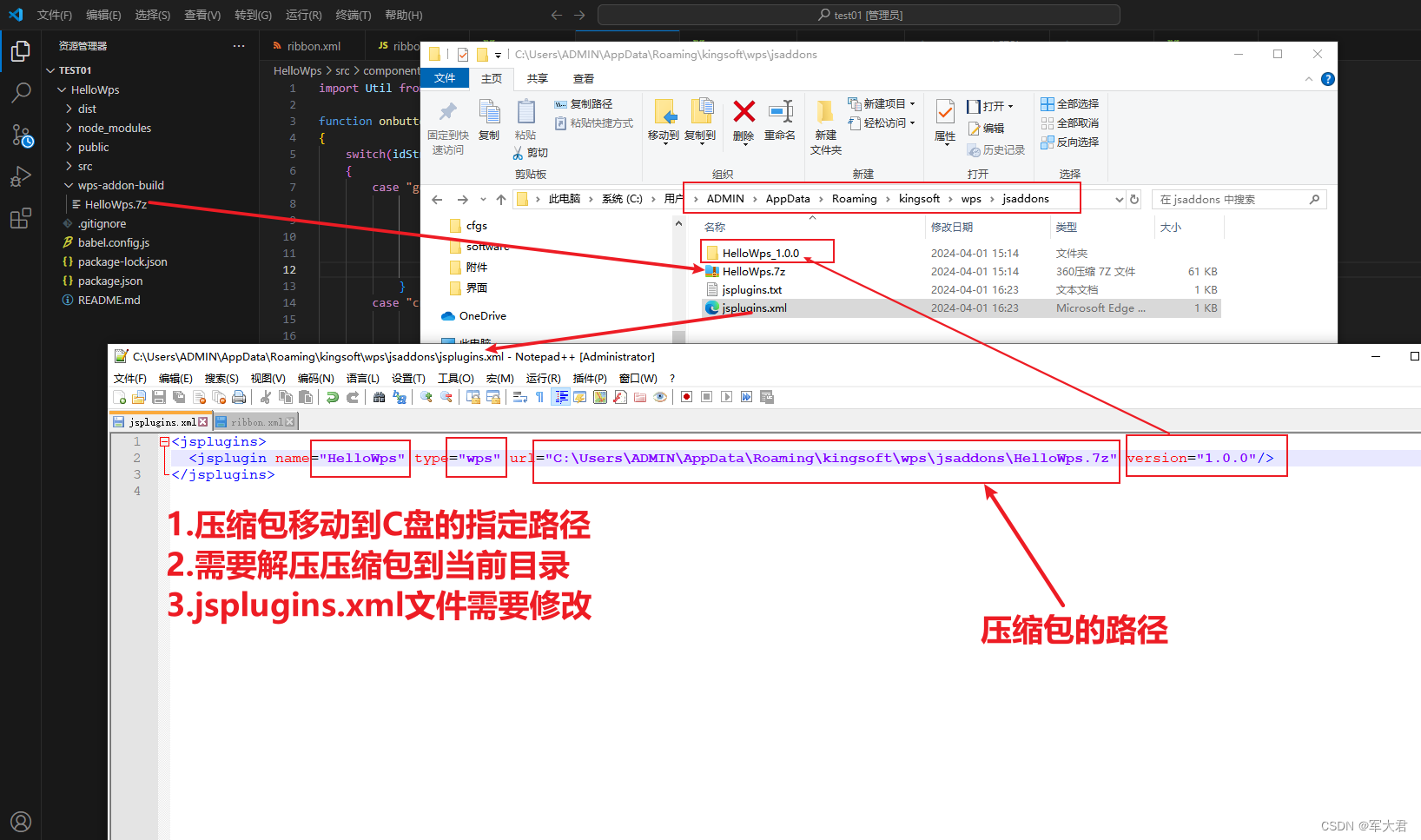
wps 开发插件
官方文档参考wps官方文档参考 1.环境安装 安装wps https://www.wps.cn/ 安装Node.js https://nodejs.org/en 安装代码编辑器 Visual Studio Code https://code.visualstudio.com/ 环境检查-进入cmd查看 node -v2.demo 2.1 demo下载 打开vscode,新建终端 安装…...

C语言----数据在内存中的存储
文章目录 前言1.整数在内存中的存储2.大小端字节序和字节序判断2.1 什么是大小端?2.2 练习 3.浮点数在内存中的存储3.1.引子3.2.浮点数的存储3.2.2 浮点数取的过程 前言 下面给大家介绍一下数据在内存中的存储,这个是一个了解c语言内部的知识点…...

【Linux学习】Linux 的虚拟化和容器化技术
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

Delphi 是一种内存安全的语言吗?
上个月,美国政府发布了 "回到基石 "报告: 通往安全和可衡量软件之路 "的报告。该报告是美国网络安全战略的一部分,重点关注多个领域,包括内存安全漏洞和质量指标。 许多在线杂志都对这份报告进行了评论࿰…...
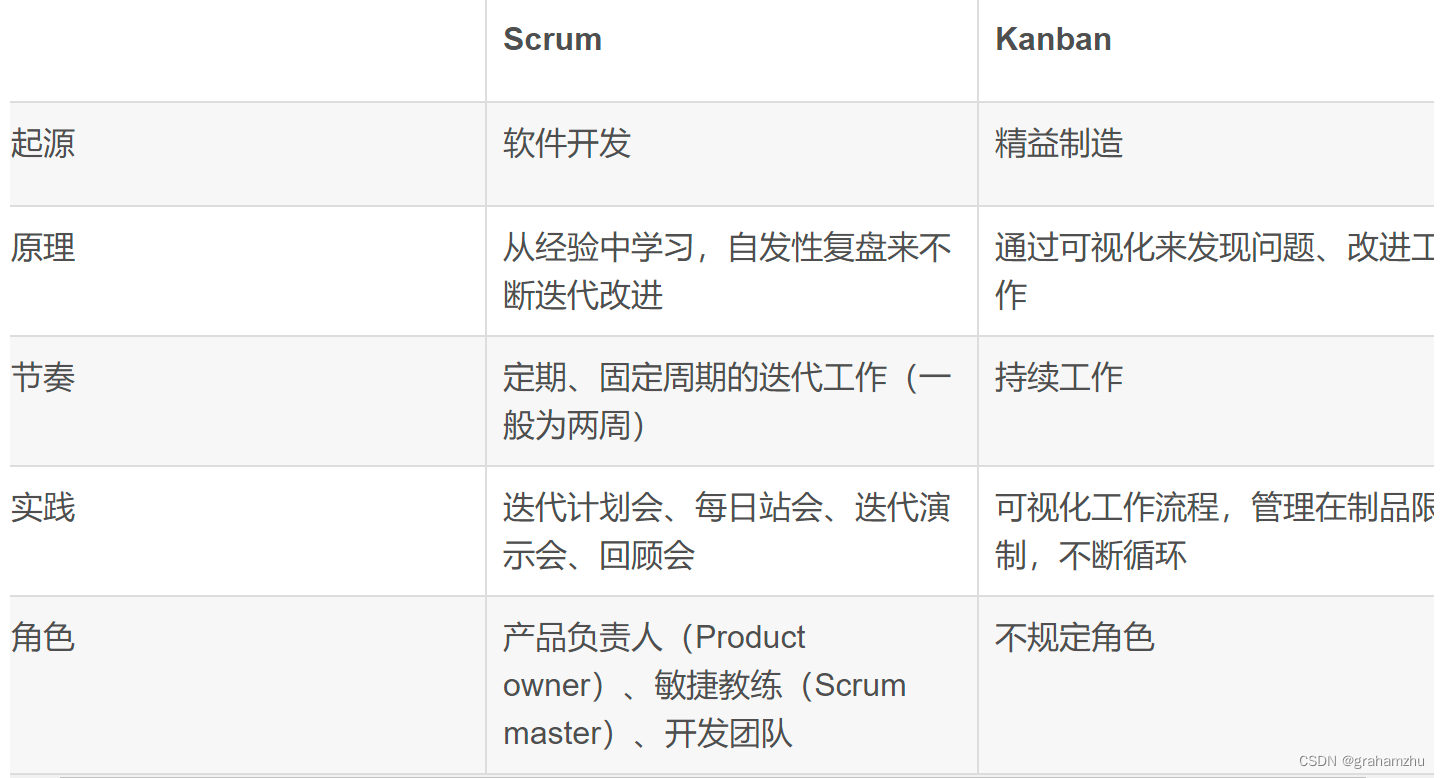
golang语言系列:Scrum、Kanban等敏捷管理策略
云原生学习路线导航页(持续更新中) 本文是 golang语言系列 文章,主要对编程通用技能 Scrum、Kanban等敏捷管理策略 进行学习 1.什么是敏捷开发 敏捷是一个描述软件开发方法的术语,它强调增量交付、团队协作、持续规划和持续学习。…...

QT背景介绍
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、QT背景 1.1什么是QT 1.2QT的发展历史 1.3什么是框架、库 1.4QT支持的平台 1.5QT的优点 1.6QT的…...
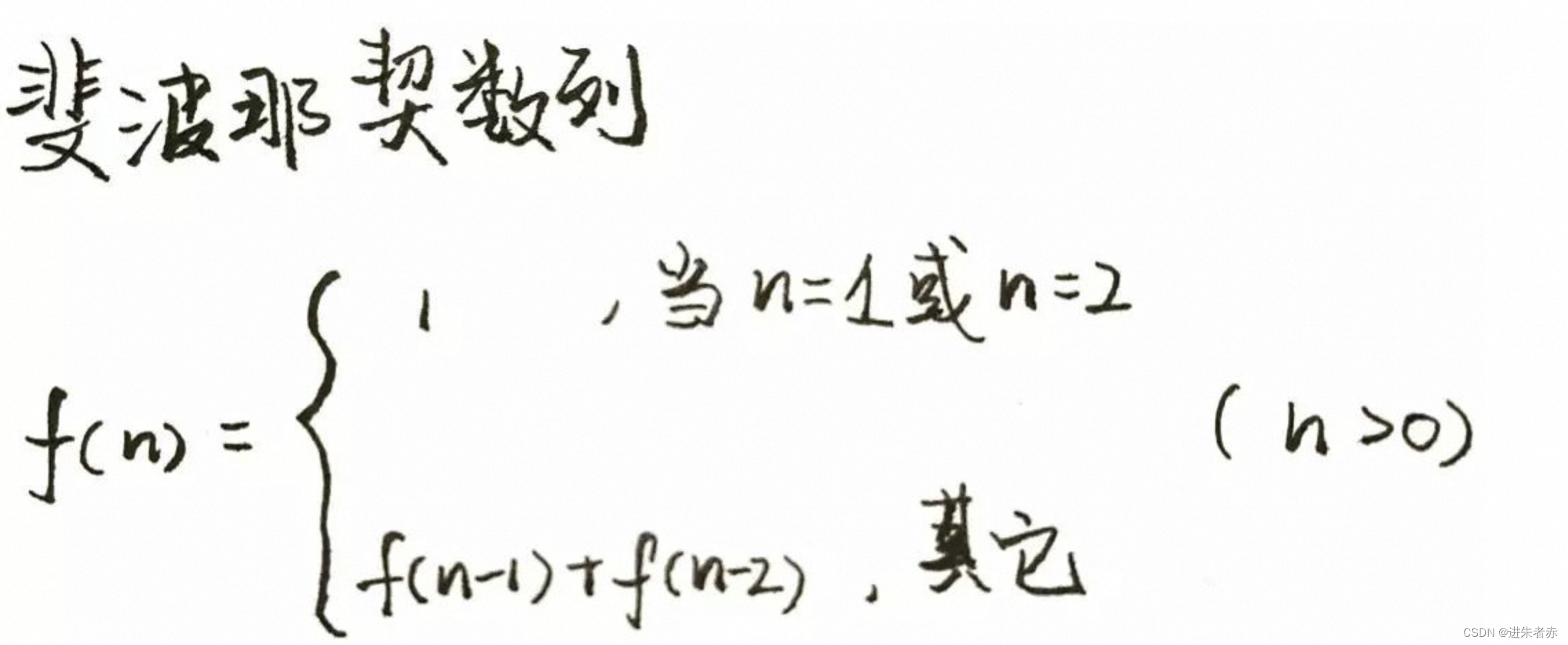
动态规划详解(Dynamic Programming)
目录 引入什么是动态规划?动态规划的特点解题办法解题套路框架举例说明斐波那契数列题目描述解题思路方式一:暴力求解思考 方式二:带备忘录的递归解法方式三:动态规划 推荐练手题目 引入 动态规划问题(Dynamic Progra…...

前端大额计算,真正解决js精度丢失问题
1.解决前端大额计算导致精度丢失问题 2.从底层上解决这个问题,计算时不使用js 运行时计算。 使用rust语言来解决这个问题,因为是底层语言,不涉及到精度问题。 3.实现步骤 步骤 1: 安装工具 确保你已经安装了Rust工具链和wasm-pack&#x…...
)
Android笔记--MediaCodec(一)
这一节主要来了解一下MediaCodec,Android MediaCodec 是 Android 平台提供的一个用于处理音频和视频数据的 API。它允许开发者对音频和视频数据进行编码和解码,支持多种格式和编解码器。MediaCodec API 通常用于实现实时音视频处理,如视频录制…...
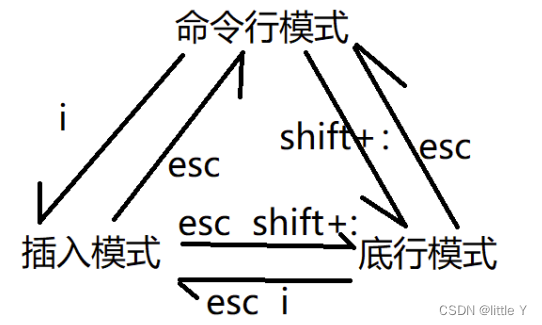
Linux简单介绍
Linux简单介绍 编译器VMware虚拟机Ubuntu——LinuxOS为什么使用LinuxOS? 目录结构Windows目录结构Linux操作系统home是不是家目录? Linux常用命令终端命令行提示符与权限切换命令tab 作用:自动补全上下箭头pwd命令ls命令mkdir命令touch命令rm…...
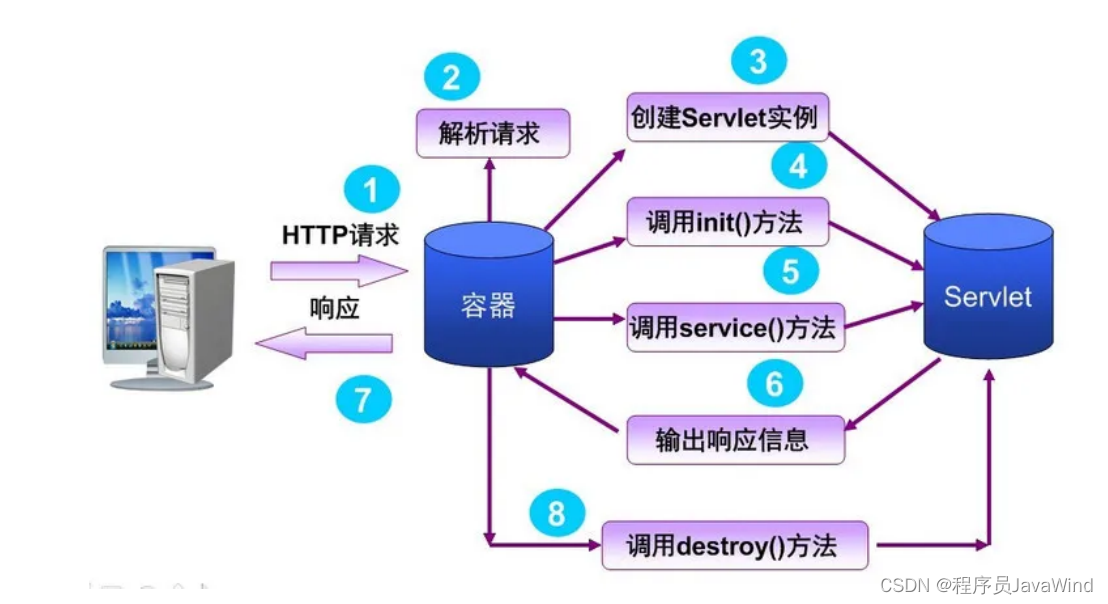
Servlet 的基本理解
Servlet 是JavaEE规范的一种,主要是为了扩展Java作为Web服务的功能,统一接口。由其他内部厂商如tomcat,jetty内部实现web的功能。如一个http请求到来:容器将请求封装为servlet中的HttpServletRequest对象,调用init()&a…...

JavaScript之applye、bind和call方法详解
Question Q1 apply()、bind()和call()方法的区别在哪? Q2 apply()和call()的应用场景 Q3 apply()、bind()和call()方法手写实现逻辑 来源 继承自Function.prototype,属于实例方法 console.log(Function.prototype.hasOwnProperty(call)) //trueconsole.l…...

Docker,anaconda环境的部署与迁移
功能上线将提上日程,但是如何将我windows环境下的程序放到linux服务器的测试环境跑通呢?这是我这整个清明假期将要解决的一件事,最蠢的办法就是看自己的环境下有哪些依赖,如何到服务器上一个一个下,但是首先这个方法很…...

【大数据运维】Hbase shell 常见操作
文章目录 一. DDL1. 表的DDL1.1. 创建表1.2. 删除表 2. 列族的DDL2.1. 增加一个列簇2.2. 删除列族2.3. 修改列族版本(ing) 二. DML1. 插入与更新数据2. 删除数据3. 清空表 三. DQL1. scan:查一批数据1.1. 查询全部1.2. 过滤rowkey1.3. 过滤列…...

LeetCode-217存在重复的元素
217 存在重复的元素 给定一个整数数组,判断是否存在重复元素。 如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。 JavaScript的 Array 对象是用于构造数组的全局对象,数组是类似…...
基于两个单片机串行通信的电子密码锁设计
1.功能 电子号码锁在实际应用中应该有两部分,一部分在外部,有键盘部分和密码显示;另一部分内部,设置密码、显示密码。使用单片机自身带有的串口可以很方便的实现单片机之间的通信,使输入的密码值传送到主机检验是否是…...
之产品设计)
产品经理功法修炼(3)之产品设计
点击下载《产品经理功法修炼(3)之产品设计》 1. 前言 产品经理的能力修炼并非局限于某一技能的速成,而是需要全面参与到产品的整个生命周期中,通过不断的实践来逐步提升自己的各项能力。尽管在企业的日常运作中,我们不可能身兼数职去扮演每一个角色,但作为产品的核心负…...

Qt 的发展历史、现状与启示
Qt 最早在1991年由挪威的两位程序员 Eirik Chambe-Eng 和 Haavard Nord 开发,他们在1994年创立 Trolltech 公司(奇趣科技)正式经营软件业务。Qt 的第一个公众预览版于1995年面世,之后在2008年被诺基亚收购;2011年到201…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
