动态规划基础
动态规划
1、动态规划的概念
简称DP,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。常常适用于有重叠子问题和最优子结构性质的问题。
简单来说,就是给定一个问题,把它拆成一个个子问题,查到子问题可以直接解决。然后把子问题答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法。
核心思想:在于拆分子问题,记住过往,减少重复计算。
2、动态规划的步骤
- 划分子问题
- 状态表示,一般用数组dp[i]表示当前状态
- 状态转移,即当前状态是由前面那些状态转移过来的,例如dp[i]=dp[i-1],表示当前状态可以由上一个状态转移过来
- 确定边界,确定初始状态
一、线性DP
1、线性DP的概念
动态规划中的一类问题,指状态之间有线性关系的动态规划问题。所谓线性DP,就是递推方程是有一个明显的线性关系的,一维线性和二维线性都有可能。在求的时候,一行一行地来求。
例题----取钱
https://www.lanqiao.cn/problems/3297/learning/
黄开的银行最近又发行了一种新面额的钞票面值为4,所以现在黄有5种面额的钞票,分别是20,10,5,4,1。但是不变的是他小气,现在又有很多人来取钱,黄又不开心了,请人来取钱,黄又不开心了,请你算出每个来取钱的人黄应该给他至少多少张钞票。
输入格式:每个测评数据含有不超过10组输入,每组给出一个n(1<=n<=10000),n为要取出的金额。
输出格式:每组样例输出一个答案(钞票数)。
示例:20 1
2 2
6 2
提示:
设置dp[i]数组 取出金额为i
最小钞票数 转移方程为:dp[i]=Math.min(dp[i-1],dp[i-4],dp[i-5],dp[i-10],dp[i-20])+1
import java.util.Arrays;
import java.util.Scanner;public class Main {
public static void main(String[] args) {Scanner sc = new Scanner(System.in);int[] arr = { 1, 4, 5, 10, 20 };int[] dp = new int[10001]; // 索引为金额, 值为方案数Arrays.fill(dp, 10000);dp[0] = 0; // 0金额的可选方案数量为0个for (int i = 1; i < dp.length; ++i) { // 枚举子问题金额数for (int j : arr) { // 每个子问题可选方案if (i >= j) { // 当金额大于等于面额时dp[i] = Math.min(dp[i - j] + 1, dp[i]); // 选择当前面额后 +1,且寻找剩余金额时方案数累加,与当前j之后的面额继续对比方案数}}}while (sc.hasNext()) {System.out.println(dp[sc.nextInt()]);}}
}例题---破损的楼梯
https://www.lanqiao.cn/problems/3367/learning/
小蓝来到了一座高耸的楼提前,楼梯共有N级台阶,从第0级台阶出发。小蓝每次可以迈上1级或2级台阶。但是,楼梯上的第级,第
级,第
级,以此类推,共m级台阶的台阶面已经坏了,不能踩上去。
现在,小蓝想要到达楼梯的顶端,也就是第N级台阶,但他不能踩到坏了的台阶上。请问他有多少种不踩坏了的台阶到达顶端的方案数?由于方案数很大,请输入其对+7取模的结果。
输入格式:
第一行包含两个正整数N(1<=N<=)和M(0<=M<=N),表示楼梯的总级数和坏了的台阶数。
接下来一行,包含M个正整数
相关文章:
动态规划基础
动态规划 1、动态规划的概念 简称DP,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。常常适用于有重叠子问题和最优子结构性质的问题。 简单来说,就是给定一个问题,把它拆成一个个子问题,查到子问题可以直接解决。然后把子问题答案保存起来,以减少重复计算…...

kubeadm部署的k8s1.29集群证书更新
1、查看证书有效期 kubeadm certs check-expiration更新证书前: [check-expiration] Reading configuration from the cluster... [check-expiration] FYI: You can look at this config file with kubectl -n kube-system get cm kubeadm-config -o yamlCERTIFIC…...

【A 类比赛】大学生学科竞赛智慧应用场景题目大全
智能应用的多彩场景:未来生活的无限可能 随着科技的飞速发展,智能应用已经渗透到我们生活的方方面面,它们不仅极大地提高了工作效率,也丰富了我们的生活体验。从家庭到工作场所,从城市到乡村,智能应用正在…...

Yarn的安装和使用(2):使用及问题解决
Yarn是JavaScript的依赖管理工具,它与npm类似,但提供了一些额外的性能优化和一致性保证。 Yarn的使用: 初始化项目: yarn init 此命令会引导您创建一个新的package.json文件,用于记录项目的元信息和依赖。 添加依赖&…...

如何在Bash中连接字符串变量
问题: 在 PHP 中,字符串按如下方式连接在一起: $foo "Hello"; $foo . " World";在这里,$foo 变成了 "Hello World"。 在 Bash 中如何实现这一点? 回答1: foo"Hello" fo…...

doesn‘t contain a valid partition table
查看硬盘空间 $ fdisk -l Disk /dev/mmcblk0: 29 GB, 31037849600 bytes, 60620800 sectors 947200 cylinders, 4 heads, 16 sectors/track Units: sectors of 1 * 512 512 bytesDisk /dev/mmcblk0 doesnt contain a valid partition table Disk /dev/mmcblk0p1: 1 MB, 10485…...

modprobe加载驱动模块时报错:modprobe: module xxx.ko not found in modules.dep
问题 使用modprobe时,报错modprobe: module xxx.ko not found in modules.dep: 原因 加载模块时,依赖没法正确添加 解决 在使用modprobe前,调用一下depmod指令,之后再用modprobe加载驱动模块 depmod modprobe interr…...
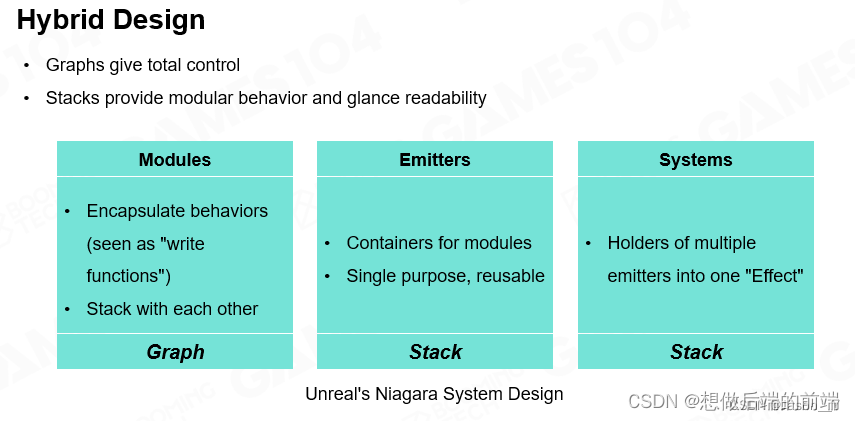
游戏引擎中的粒子系统
一、粒子基础 粒子系统里有各种发射器(emitter),发射器发射粒子(particle)。 粒子是拥有位置、速度、大小尺寸、颜色和生命周期的3D模型。 粒子的生命周期中,包含产生(Spawn)、与环…...
哈佛大学商业评论 -- 第二篇:增强现实是如何工作的?
AR将全面融入公司发展战略! AR将成为人类和机器之间的新接口! AR将成为人类的关键技术之一! 请将此文转发给您的老板! --- 本文作者:Michael E.Porter和James E.Heppelmann 虽然物理世界是三维的,但大…...

『python爬虫』巨量http代理使用 每天白嫖1000ip(保姆级图文)
目录 注册 实名得到API链接和账密 Python3requests调用Scpay总结 欢迎关注 『python爬虫』 专栏,持续更新中 欢迎关注 『python爬虫』 专栏,持续更新中 注册 实名 注册巨量http 用户概览中领取1000ip,在动态代理中使用.用来测试一下还是不错的 得到AP…...
)
6-95 希尔排序(Java语言描述)
编程实现希尔排序函数。public static void shellSort(int arr[])。其中arr存放待排序的数据,数组长度不大于1000。 函数接口定义: /* 对长度为n的数组arr执行希尔排序 */ public static void shellSort(int arr[]); 请实现 shellSort函数,使排序后的数据从小到大排列。…...

JAVA面试大全之分布式篇
目录 1、一致性算法 1.1、什么是分布式系统的副本一致性?有哪些? 1.2、在分布式系统中有哪些常见的一致性算法?...

qt各种锁使用讲解
在Qt中,主要有以下几种锁的类型: 1. QMutex(互斥锁): 是最常见的锁类型,用于实现简单的互斥访问。可以通过lock()和unlock()手动控制锁的加锁和解锁。 QMutexLocker:是一个RAII类,…...

5.111 BCC工具之ext4dist.py解读
一,工具简介 ext4dist跟踪ext4的读取、写入、打开和fsync操作,并将其延迟总结为2的幂次方直方图。 二,代码示例 #!/usr/bin/env pythonfrom __future__ import print_function from bcc import BPF from time import sleep, strftime import argparse# symbols kallsyms …...

Rust 的 termion 库控制终端光标的位置
在控制台应用程序中,固定打印在屏幕的第一行通常涉及到控制终端光标的位置。Rust 标准库本身并不提供直接控制终端光标位置的功能,但你可以使用第三方库如 termion 来实现这个需求。 termion 是一个用于处理终端的 Rust 库,它提供了很多有用…...

ADB(Android Debug Bridge)操作命令详解及示例
ADB(Android Debug Bridge)是一个强大的命令行工具,它是Android SDK的一部分,主要用于Android设备(包括真实手机和平板电脑以及模拟器)的调试、系统控制和应用程序部署。 下面是一些ADB的常用命令ÿ…...
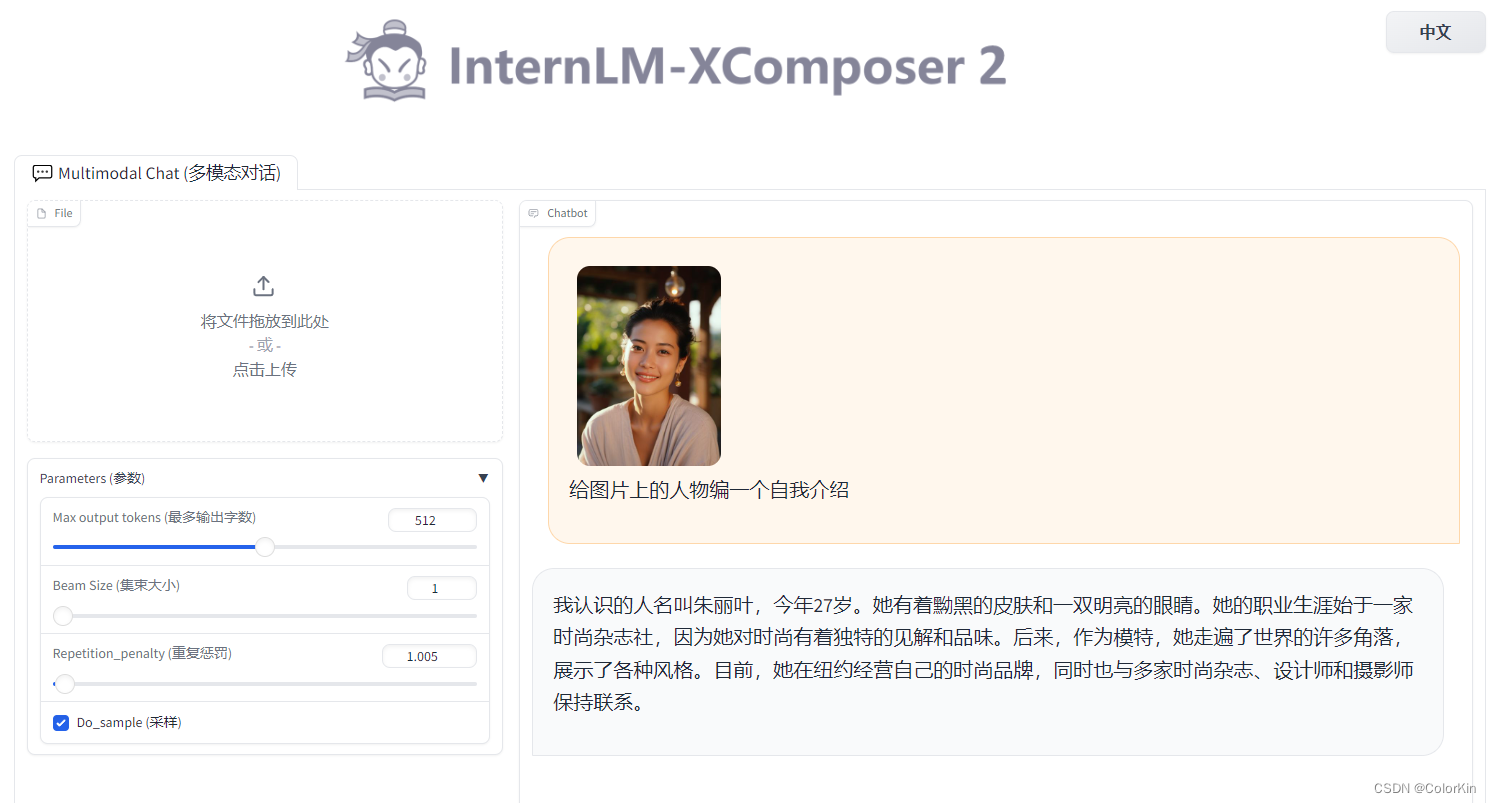
书生浦语训练营2期-第二节课笔记作业
目录 一、前置准备 1.1 电脑操作系统:windows 11 1.2 前置服务安装(避免访问127.0.0.1被拒绝) 1.2.1 iis安装并重启 1.2.2 openssh安装 1.2.3 openssh服务更改为自动模式 1.2.4 书生浦语平台 ssh配置 1.3 补充(前置服务ok…...

【日常积累】指定ruby版本环境安装
背景说明 在redis的5.0版本之前,使用redis提供的redis-trib创建redis集群时还需要依赖ruby环境。当然有时候我们自已也需要安装指定ruby版本环境。下面是安装时的大致过程,以及过程中遇到的问题解决。我使用的环境是centos7,小版本差别应该不…...

SOC内部集成网络MAC外设+ PHY网络芯片方案:MII/RMII 接口与 MDIO 接口
一. 简介 本文来了解一下常用的一种网络硬件方案:SOC内部集成网络MAC外设 PHY网络芯片方案。 其中涉及的 MII接口,RMII接口(MII接口与RMII接口二选一),MDIO接口,RJ45。 二. MII/RMII 接口,M…...

简单了解HTTP和HTTPS
HTTP的安全问题? 我们都知道HTTP是不安全的,而HTTPS是安全的,那HTTP有哪些安全问题呢?(考虑传输过程以及响应方) 明文传输,有窃听风险:HTTP协议无法加密数据,所有通信数…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
