蓝桥杯真题Day47 倒计时6天:6道真题+回溯递归问题
[蓝桥杯 2019 省 A] 糖果
题目描述
糖果店的老板一共有M种口味的糖果出售。为了方便描述,我们将M 种口味编号 1∼ M。小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是K 颗一包整包出售。
幸好糖果包装上注明了其中 K 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。
给定 N 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
输入格式
第一行包含三个整数 N,M 和 K。
接下来 N 行每行K这整数T1,T2,⋯,TK,代表一包糖果的口味。
输出格式
一个整数表示答案。如果小明无法品尝所有口味,输出−1。

代码表示
#include <bits/stdc++.h>
using namespace std;const int N = 20;
int n, m, k, dp[1 << 20], v[1 << 20]; // 状压的数组需要开2^n,因为表示的是状态int main() {scanf("%d%d%d", &n, &m, &k);memset(dp, 0x3f3f3f3f, sizeof(dp)); // 初始化dp数组为最大值for (int i = 1; i <= n; ++i) {int h = 0, p;for (int j = 1; j <= k; ++j) {scanf("%d", &p);p--;h = h | (1 << p); // 将糖果的口味对应的位置置为1,表示这个糖果包含了该口味}dp[h] = 1; // 这些口味都可以用一包糖解决v[i] = h; // 记录糖的状态}for (int i = 0; i < (1 << m); ++i) { // i枚举的是状态,即0~1...11111(m个1)for (int j = 1; j <= n; ++j) {dp[i | v[j]] = min(dp[i | v[j]], dp[i] + 1); // 将当前状态i与糖果j的状态进行合并,并更新最小包数dp}}if (dp[(1 << m) - 1] == 0x3f3f3f3f)cout << -1; // 搭配不出来elsecout << dp[(1 << m) - 1]; // 搭配出来return 0;
}心得体会
这题是0-1背包问题

2、在这段代码中,dp[1 << 20]和v[1 << 20]是用于状态压缩的数组。状态压缩是一种常用的优化技巧,用于在处理具有多种状态组合的问题时减少内存和计算量。在这个问题中,糖果的口味有 M 种,每种口味可以选择购买或不购买。那么,总共可能的状态就有 2^M 种(每种口味的糖果都有两种选择:购买或不购买)。因为 M 的最大值为 20,所以最多可能有 2^20 种状态。
为了表示这些状态,可以使用一个整数来表示,整数的二进制位表示每个口味是否购买。例如,假设 M=3,那么状态 5(二进制为 101)表示购买了第 1 和第 3 种口味的糖果,但没有购买第 2 种口味的糖果。因此,为了存储这些状态,可以使用大小为 2^M 的数组。在这段代码中,dp和v数组的大小都是1 << 20,即 2^20。这样就可以通过数组的索引来表示不同的状态。
这种状态压缩的技巧可以减少内存的使用,并且在处理状态转移时更加高效。在该代码中,dp数组用于记录每个状态下需要的最小包数,v数组用于记录每个糖果包。
[蓝桥杯 2014 省 AB] 蚂蚁感冒
题目描述
长 100厘米的细长直杆子上有n 只蚂蚁。它们的头有的朝左,有的朝右。每只蚂蚁都只能沿着杆子向前爬,速度是1 厘米 / 秒。当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
输入格式
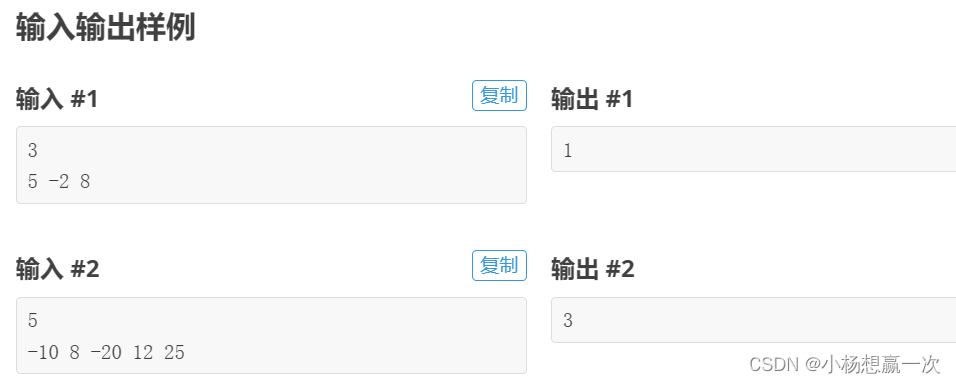
第一行输入一个整数n(1<n<50) 表示蚂蚁的总数。
接着的一行是n 个用空格分开的整数 Xi(−100<Xi<100),Xi 的绝对值,表示蚂蚁离开杆子左边端点的距离。正值表示头朝右,负值表示头朝左,数据中不会出现0值,也不会出现两只蚂蚁占用同一位置。其中,第一个数据代表的蚂蚁感冒了。
输出格式
要求输出 1个整数,表示最后感冒蚂蚁的数目。
代码表示
#include <bits/stdc++.h>
using namespace std;int x[55];//定义蚂蚁数组int main(){int n;//定义蚂蚁数cin>>n;//输入蚂蚁数for(int i=1; i<=n; i++) scanf("%d",&x[i]);//输入每个蚂蚁的情况int l=0,r=0;//统计在第1只蚂蚁左侧朝右、右侧朝左的蚂蚁数。for(int i=2; i<=n; i++){if(abs(x[i])<abs(x[1]) && x[i]>0) l++;//左侧朝右if(abs(x[i])>abs(x[1]) && x[i]<0) r++;//右侧朝左}int sum=0;//定义感冒蚂蚁总数if(x[1]<0){//第1只蚂蚁朝左if(l==0) sum=1;else sum=l+r+1;}else{//第1只蚂蚁朝右if(r==0) sum=1;else sum=l+r+1;}cout<<sum;return 0;
}心得体会
这个题目真的就是找规律和仔细理解题目。
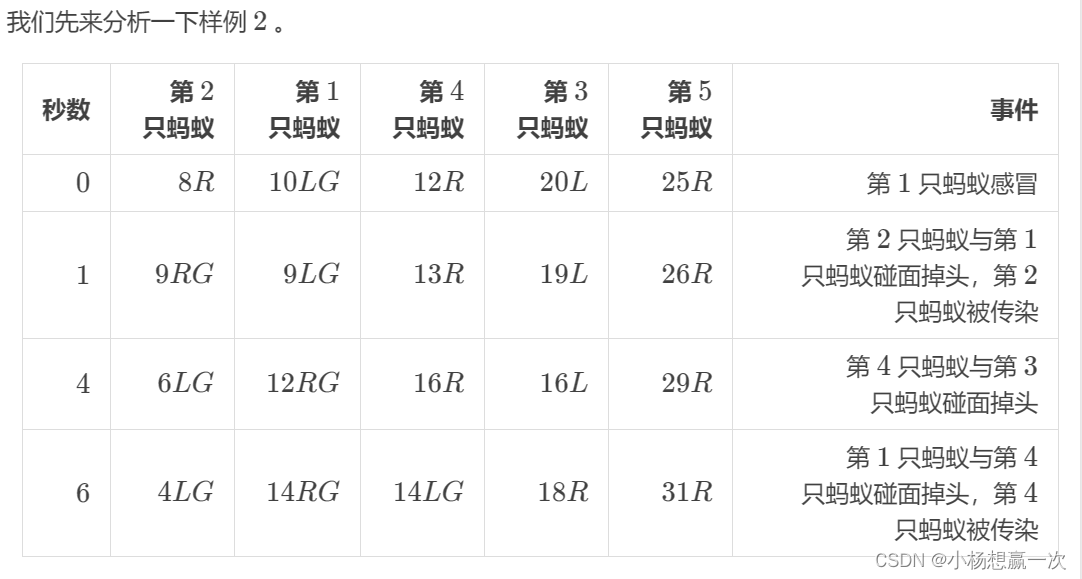
其中 L 表示向左,R 表示向右,G 表示感冒。最后第1,2,4 只蚂蚁感冒。
由表格可以发现,由于碰面就掉头,这些蚂蚁的相对排列顺序是保持不变的,那么,应该可以从开始的位置就能预测谁会被传染。
在样例 2 中,第 1 只蚂蚁(感冒蚂蚁)朝左。
1、位于第 1只蚂蚁左侧且朝右蚂蚁有一只,即第 2只蚂蚁,被传染;
2、由于步骤 1 ,第 1只蚂蚁朝右,位于第 1 只蚂蚁右侧且朝左蚂蚁也有一只,即第 4只蚂蚁,也被传染。
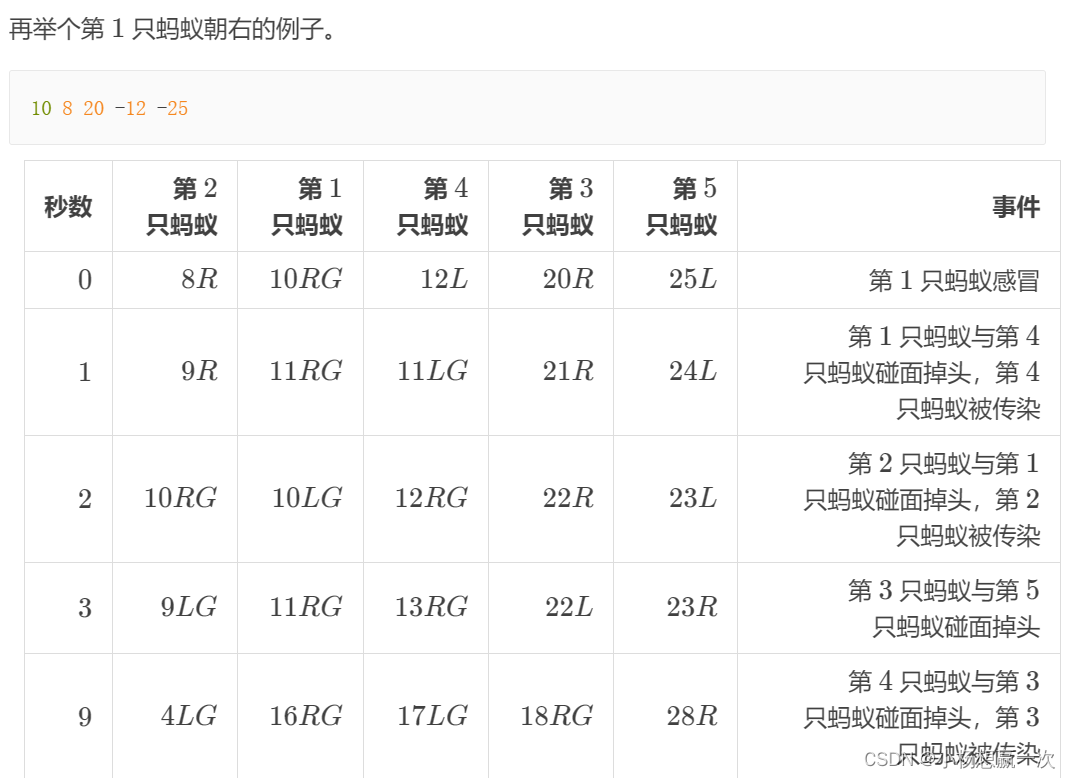
最后第1,2,3,4 只蚂蚁感冒。
在这个例子中第1 只蚂蚁(感冒蚂蚁)朝右。
1、位于第 1 只蚂蚁右侧且朝左蚂蚁有两只,即第 4 只蚂蚁和第 5 只蚂蚁,它们都被传染;(其中第 3 只蚂蚁在与第 5 只蚂蚁碰面后朝左)
2、由于步骤 1,第 1只蚂蚁朝左,位于第1 只蚂蚁左侧且朝右蚂蚁有一只,即第 2 只蚂蚁,也被传染。
总结一下

[蓝桥杯 2020 省 B1] 整数拼接
题目描述
给定一个长度为n 的数组A1,A2,⋯,An。你可以从中选出两个数Ai 和Aj(i≠j),然后将 Ai 和 Aj 一前一后拼成一个新的整数。例如 12 和 345 可以拼成 12345 或 34512。注意交换Ai 和Aj 的顺序总是被视为2种拼法,即便是Ai=Aj 时。请你计算有多少种拼法满足拼出的整数是 K 的倍数。
输入格式
第一行包含 2个整数n 和K。
第二行包含n个整数A1,A2,⋯,An。
输出格式
一个整数代表答案。

代码表示
#include <bits/stdc++.h>
using namespace std;
//动态规划
long long n,k,l,ans;
int a[12][1000005],b[1000005];void d()
{for(int i=1;i<=n;i++){ans+=a[(int)log10(b[i])+1][(k-b[i]%k)%k];//答案加方案数for(int j=1,p=10;j<=10;j++){a[j][(b[i]%k*p)%k]++;//这个次方和次方余数方案加1p=p*10%k;}}
}
int main()
{cin>>n>>k;for(int i=1;i<=n;i++)cin>>b[i];d();reverse(b+1,b+n+1);//翻转memset(a,0,sizeof(a));//将数组 a 清空为 0d();cout<<ans; return 0;
}
心得体会
1、从左到右存储每个数乘 10 的 1 到 10 次方模 k 的余数和1 到10 ,查找后面数是否相同,相同就将答案加上个数,然后再从右到左来一次,最后输出。
2、(int)log10(b[i]) + 1:计算数字 b[i] 的位数。log10 函数返回以 10 为底的对数,将结果转换为整数后加 1 是因为位数从 1 开始计数。
例:如果 b[i] 的值是 12345,则 (int)log10(b[i]) 的结果是 4,因为 12345 是一个 5 位数,其对数的整数部分是 4。
3、(k - b[i] % k) % k:计算数字 b[i] 对 k 的余数,再与 k 相减,并取模运算,得到需要的余数。
[蓝桥杯 2018 省 B] 递增三元组
题目描述
给定三个整数数组 A=[A1,A2,⋯,AN],B=[B1,B2,⋯,BN],C=[C1,C2,⋯,CN]。请你统计有多少个三元组(i,j,k) 满足:1、1≤i,j,k≤N;2、Ai<Bj<Ck
输入格式
第一行包含一个整数N。
第二行包含N 个整数A1,A2,⋯,AN。
第三行包含N 个整数B1,B2,⋯,BN。
第四行包含N 个整数C1,C2,⋯,CN。
输出格式
一个整数表示答案

代码表示
第一种 72分 会超时
#include <bits/stdc++.h>
using namespace std;int main() {int n;cin >> n;int a[10001];int b[10001];int c[10001];for (int j = 0; j < n; ++j) {cin >> a[j];}for (int j = 0; j < n; ++j) {cin >> b[j];}for (int j = 0; j < n; ++j) {cin >> c[j];}int ann = 0;for (int j = 0; j < n; ++j) {for (int i = 0; i < n; ++i) {for (int k = 0; k < n; ++k) {if (a[i]<b[j]&& b[j]< c[k]) {ann++;}}}}cout << ann;return 0;
}把开始的部分换成vector也可以
vector<int> A(N), B(N), C(N);for (int i = 0; i < N; i++) {cin >> A[i];}for (int i = 0; i < N; i++) {cin >> B[i];}for (int i = 0; i < N; i++) {cin >> C[i];}法二 利用两种函数来写,解析说这是二分法??震惊🙆♀️
#include <bits/stdc++.h>
using namespace std;typedef long long ll;
int n;
ll cnt = 0;
int a[100007], b[100007], c[100007];int main()
{scanf("%d", &n); // 从输入中读取 n 的值// 从输入中读取数组 a 的元素for (int i = 1; i <= n; ++i)scanf("%d", a + i);// 从输入中读取数组 b 的元素for (int i = 1; i <= n; ++i)scanf("%d", b + i);// 从输入中读取数组 c 的元素for (int i = 1; i <= n; ++i)scanf("%d", c + i);// 对数组 a、b、c 进行升序排序sort(a + 1, a + n + 1);sort(b + 1, b + n + 1);sort(c + 1, c + n + 1);// 遍历数组 b 的每个元素for (int i = 1; i <= n; i++) {// 使用 lower_bound 函数计算在数组 a 中小于 b[i] 的元素个数//将偏移量减去 a 的起始位置,得到在数组 a 中的下标ll n1 = lower_bound(a + 1, a + n + 1, b[i]) - a - 1;// 使用 upper_bound 函数计算在数组 c 中大于 b[i] 的元素个数//将偏移量减去 c 的起始位置,得到在数组 c 中的下标ll n2 = upper_bound(c + 1, c + n + 1, b[i]) - c - 1;// 计算满足条件的组合数量并累加到 cnt 变量中cnt += n1 * (n - n2);}cout << cnt;return 0;
}
心得体会
1、lower_bound(a+1, a+n+1, b[i]):这是一个函数调用,用于在数组 a 中查找第一个不小于 b[i] 的元素的位置,并返回该位置的指针
2、upper_bound(c+1, c+n+1, b[i]):这是一个函数调用,用于在数组 c 中查找第一个大于 b[i] 的元素的位置,并返回该位置的指针
lower_bound 和 upper_bound 是 C++ 标准库中的两个函数,用于在已排序的序列(例如数组或容器)中进行二分查找。
lower_bound函数用于查找第一个不小于给定值的元素的位置。upper_bound函数用于查找第一个大于给定值的元素的位置。
1)、lower_bound
template<class ForwardIt, class T>
ForwardIt lower_bound(ForwardIt first, ForwardIt last, const T& value);
first和last是正向迭代器,表示要搜索的范围。范围是左闭右开的,即包括first,但不包括last。value是要查找的值。
lower_bound 函数返回一个指向范围中第一个不小于 value 的元素位置的迭代器。如果所有元素都小于 value,则返回 last。
2)、upper_bound
template<class ForwardIt, class T>
ForwardIt upper_bound(ForwardIt first, ForwardIt last, const T& value);
first和last是正向迭代器,表示要搜索的范围。范围是左闭右开的,即包括first,但不包括last。value是要查找的值。
upper_bound 函数返回一个指向范围中第一个大于 value 的元素位置的迭代器。如果所有元素都不大于 value,则返回 last。
这两个函数的时间复杂度是对数级别的,因为它们使用了二分查找算法。在使用这两个函数之前,需要确保序列是按升序排序的,这样才能得到正确的结果。
[蓝桥杯 2018 省 A] 倍数问题
题目描述
众所周知,小葱同学擅长计算,尤其擅长计算一个数是否是另外一个数的倍数。但小葱只擅长两个数的情况,当有很多个数之后就会比较苦恼。现在小葱给了你 n 个数,希望你从这 n个数中找到三个数,使得这三个数的和是K 的倍数,且这个和最大。数据保证一定有解。
输入格式
从标准输入读入数据。
第一行包括 2个正整数表示n 和K。
第二行n个正整数,代表给定的n个数。
输出格式
输出一行一个整数代表所求的和。

代码表示
第一种:60分 超时/(ㄒoㄒ)/~~我滴暴力呀
#include <bits/stdc++.h>
using namespace std;
#define long long int;
int main()
{int n,k;cin>>n>>k;int a[n];for(int i=1;i<=n;++i){cin>>a[i];}int ann=0;for(int j=1;j<=n;++j){for(int i=j+1;i<=n;++i){for(int f=i+1;f<=n;++f){if((a[i]+a[j]+a[f])%k==0){ann=max(a[i]+a[j]+a[f],ann);}}}}cout<<ann;return 0;
}
第二种

#include<bits/stdc++.h>
using namespace std;int n, k, a[100005];
long long ans = -6e8, maxx[1005][3];int main() {cin >> n >> k;// 初始化maxx数组,用于存储每个余数对应的最大、次大、第三大的数的值for (int i = 0; i < k; i++)maxx[i][0] = maxx[i][1] = maxx[i][2] = -6e8;for (int i = 1; i <= n; i++) {cin >> a[i];// 计算当前数除以k的余数int mod = a[i] % k;// 根据当前余数,更新maxx数组中的最大、次大、第三大的数的值if (maxx[mod][0] < a[i])maxx[mod][2] = maxx[mod][1], maxx[mod][1] = maxx[mod][0], maxx[mod][0] = a[i];else if (maxx[mod][1] < a[i])maxx[mod][2] = maxx[mod][1], maxx[mod][1] = a[i];else if (maxx[mod][2] < a[i])maxx[mod][2] = a[i];}//计算第三个余数xfor (int i = 0; i < k; i++) {for (int j = 0; j < k; j++) {for (int l = 0; l <= 2 * k; l += k) {int x = l - i - j;//如果x不在合法范围内,则跳过当前循环if (x < 0 || x >= k)continue;// 更新最大和ans的值,其中根据i和j的关系决定余数j要取次大值,x也是同理ans = max(ans, maxx[i][0] + maxx[j][(i == j)] + maxx[x][(i == x) + (j == x)]);}}}cout << ans;return 0;
}心得体会
for(int j=1;j<=n;++j){ for(int i=j+1;i<=n;++i){ for(int f=i+1;f<=n;++f){
注意写这种连续循环的时候要记得画黑的部分;
[蓝桥杯 2017 省 AB] 包子凑数
题目描述
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N 种蒸笼,其中第 i 种蒸笼恰好能放Ai 个包子。每种蒸笼都有非常多笼,可以认为是无限笼。每当有顾客想买X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X 个包子。
比如一共有 3 种蒸笼,分别能放 3、4 和 5 个包子。当顾客想买 11 个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有 3 种蒸笼,分别能放 4、5和 6个包子。而顾客想买 7 个包子时,大叔就凑不出来了。小明想知道一共有多少种数目是包子大叔凑不出来的。
输入格式
第一行包含一个整数 N。(1≤N≤100)。
以下N 行每行包含一个整数Ai。(1≤Ai≤100)。
输出格式
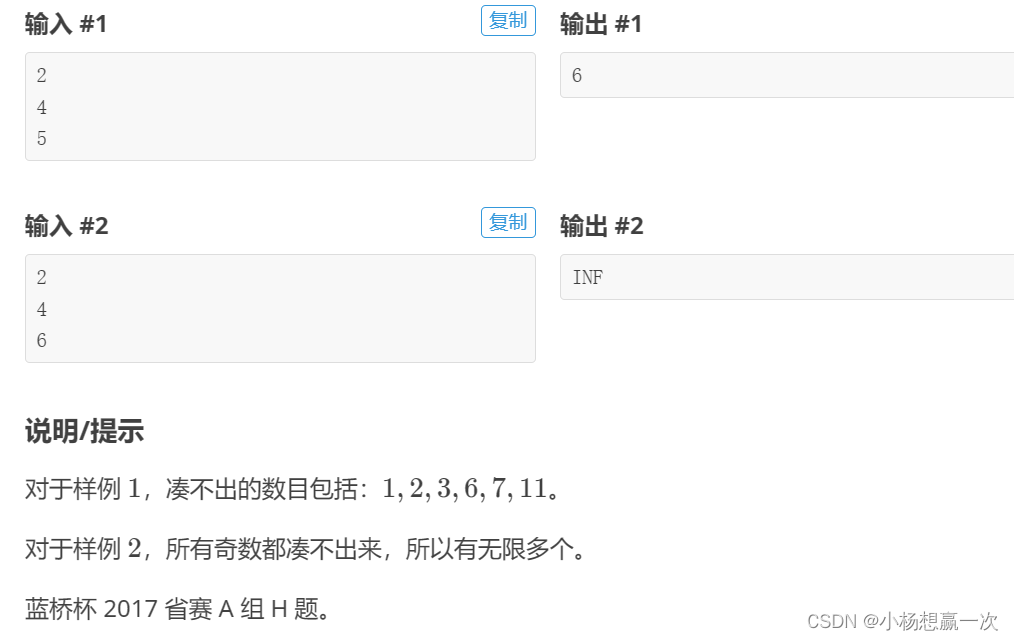
一个整数代表答案。如果凑不出的数目有无限多个,输出 INF。
代码表示
#include <bits/stdc++.h>
using namespace std;const int maxn = 1e5;
int n, x[maxn];// 辗转相除法求最大公约数
int gcd(int a, int b) {if (!b)return a;return gcd(b, a % b);
}// 判断数组中的数是否存在公因数大于1
bool pd() {int Gcd = 0;for (int i = 1; i <= n; i++)Gcd = gcd(Gcd, x[i]);return Gcd > 1;
}// 裴蜀定理可得:ax+by 永远能被 gcd(a, b) 整除 bitset<maxn + 1> S; // S[i]为1表示可以拼凑出数i,为0表示不能int main() {cin >> n;S[0] = 1; // 初始化S,0可以拼凑出for (int i = 1; i <= n; i++)cin >> x[i];sort(x + 1, x + n + 1); // 对数组x进行排序if (pd()) {cout << "INF";exit(0); // 如果数组中存在公因数大于1,则输出"INF"表示无限个数无法拼凑,退出程序}for (int i = 1; i <= n; i++)for (int j = x[i]; j <= 1000; j++)S |= S << x[i]; // 更新S,将能拼凑出的数进行标记int ans = 0;for (int i = 1; i <= x[n] * 990; i++)if (!S.test(i))ans++; // 统计无法拼凑的数的个数cout << ans; // 输出结果return 0;
}心得体会
1、S |= S << x[i] 是对位集合 S 进行按位或运算的操作。
在这个表达式中,S << x[i] 表示将 S 中的每个位都向左移动 x[i] 位。例如,如果 S 的二进制表示为 1010,而 x[i] 的值为 2,那么 S << x[i] 的结果就是 101000。
然后, 表示将位集合 S |= S << x[i]S 与 进行按位或运算,并将结果赋值给 S << x[i]S。按位或运算的规则是,对应位置上的两个位只要有一个为1,结果的对应位置上就为1。因此,这个操作将把 S 中的某些位设为1,表示能够拼凑出特定的数。
通过循环遍历数组 x 中的数,每次都对 S 进行位移和按位或运算,最终能够拼凑出的数会在 S 中被标记为1。
2、bitset<maxn + 1> S; 是定义了一个名为 S 的位集合(bitset),它的长度为 maxn + 1。
bitset 是一种固定长度的二进制位集合,每个位只能是0或1。在这里,bitset<maxn + 1> 表示创建了一个长度为 maxn + 1 的位集合 。S
这个位集合 S 可以被用来表示一组布尔值,其中每个位置上的位都可以表示某个状态的真或假。
在给定的代码中,位集合 S 被用来表示能否拼凑出某个数。每个位置上的位可以表示对应的数是否能够被拼凑出来,1 表示可以拼凑,0 表示不能拼凑。
通过使用位集合 S,可以高效地进行位运算操作,例如左移、按位或等,来更新和查询拼凑数的状态。
回溯递归问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
注意:组合是不强调元素顺序的,排列是强调元素顺序。
例如:{1, 2} 和 {2, 1} 在组合上,就是一个集合,因为不强调顺序,而要是排列的话,{1, 2} 和 {2, 1} 就是两个集合了。
记住组合无序,排列有序,就可以了,所有回溯法的问题都可以抽象为树形结构!
回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树。
回溯三部曲:
1、回溯函数模板返回值以及参数
在回溯算法中,习惯是函数起名字为backtracking,但回溯算法中函数返回值一般为void。
参数:因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
回溯函数伪代码如下:
void backtracking(参数)
2、回溯函数终止条件
达到了终止条件:树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {存放结果;return;
}
3、回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
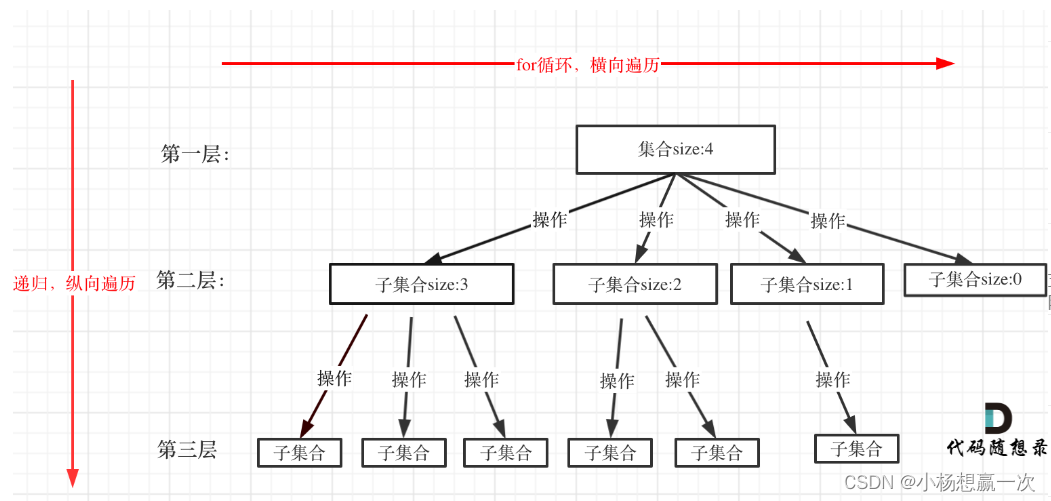
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
backtracking这里自己调用自己,实现递归。
从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果。
回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。可以按 任何顺序 返回答案。

提示:
1 <= n <= 201 <= k <= n
思路提示
直接的解法当然是使用for循环,例如示例中k为2,很容易想到 用两个for循环,这样就可以输出 和示例中一样的结果。代码如下:
int n = 4;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {cout << i << " " << j << endl;}
}
输入:n = 100, k = 3 那么就三层for循环,代码如下:
int n = 100;
for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {for (int u = j + 1; u <= n; n++) {cout << i << " " << j << " " << u << endl;}}
}
如果n为100,k为50呢?
要解决 n为100,k为50的情况,暴力写法需要嵌套50层for循环,那么回溯法就用递归来解决嵌套层数的问题。递归来做层叠嵌套(可以理解是开k层for循环),每一次的递归中嵌套一个for循环,那么递归就可以用于解决多层嵌套循环的问题了。
回溯法三部曲
1、递归函数的返回值以及参数
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。代码如下:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果
函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
startIndex 就是防止出现重复的组合。
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
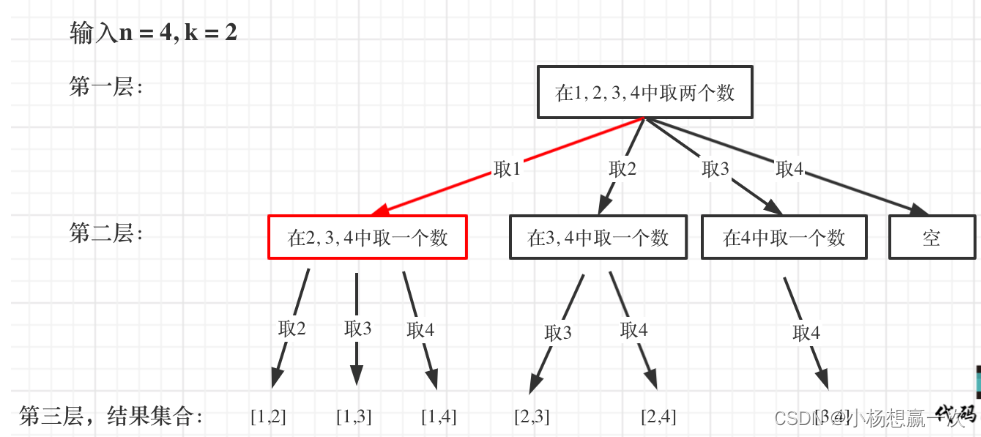
需要startIndex来记录下一层递归,搜索的起始位置,整体代码如下:
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件单一结果
void backtracking(int n, int k, int startIndex)2、回溯函数终止条件
到达所谓的叶子节点:path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。
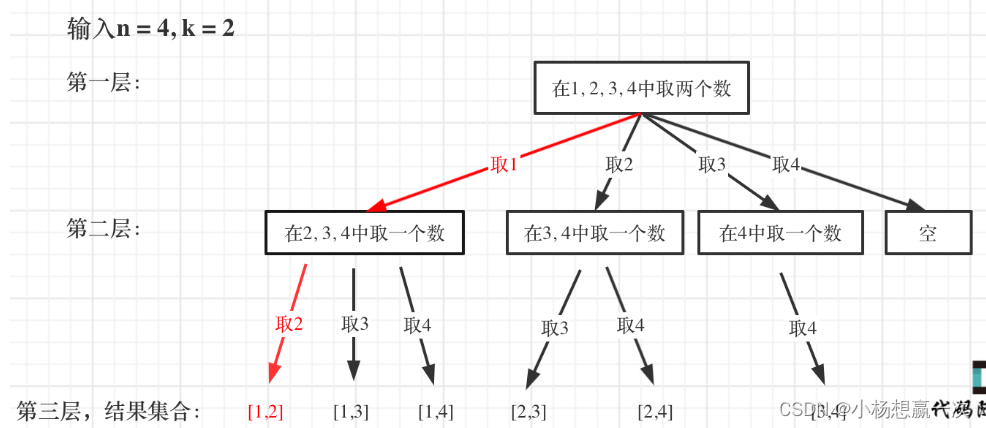
用result二维数组,把path保存起来,并终止本层递归,所以终止条件代码如下:
if (path.size() == k) {result.push_back(path);return;
}3、单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
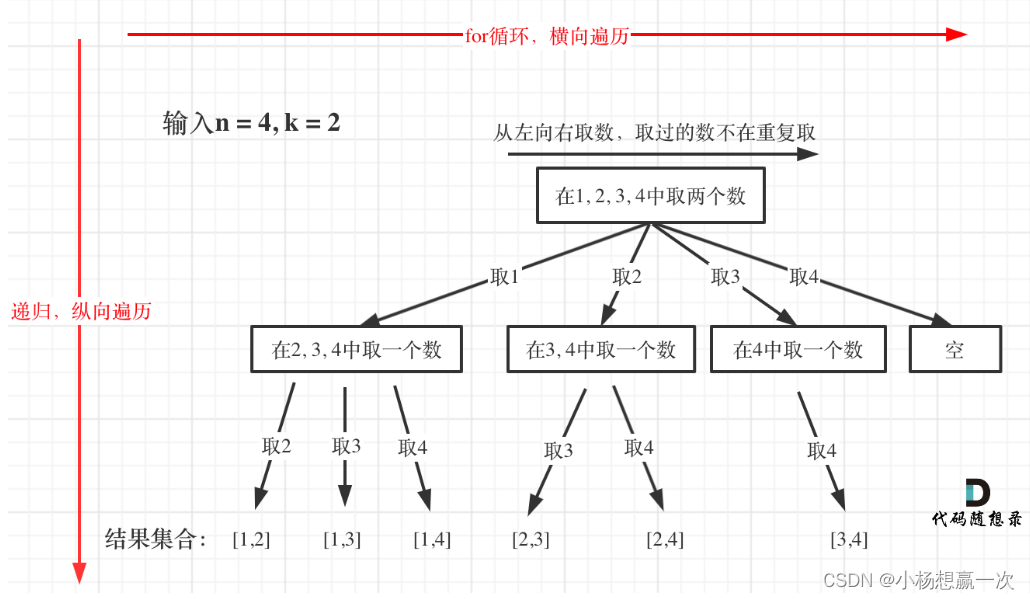
如此才遍历完图中的这棵树,for循环每次从startIndex开始遍历,然后用path保存取到的节点 i。代码如下:
for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归:控制树的纵向遍历,注意下一层搜索要从i+1开始path.pop_back(); // 回溯,撤销处理的节点
}
可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
代码表示
#include <bits/stdc++.h>
using namespace std;vector<vector<int> > result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}
}
vector<vector<int> > combine(int n, int k) {result.clear();path.clear();backtracking(n, k, 1);return result;
}
int main() {int n, k;cin >> n >> k;vector<vector<int> > combinations = combine(n, k);// 输出所有可能的组合for (const auto& combination : combinations) {for (int num : combination) {cout << num << " ";}cout << endl;}return 0;
}相关文章:

蓝桥杯真题Day47 倒计时6天:6道真题+回溯递归问题
[蓝桥杯 2019 省 A] 糖果 题目描述 糖果店的老板一共有M种口味的糖果出售。为了方便描述,我们将M 种口味编号 1∼ M。小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是K 颗一包整包出售。 幸好糖果包装上注明了其中 K 颗糖果的口味…...

通过UDP实现参数配置
来讲讲UDP的一种常见应用 我们知道UDP是一种无连接的网络传输协议,在发送数据时指定目标IP及端口就可以将数据发送出去,因此特别适合用作网络设备发现。 我们可以自定义一个通信端口,假设为55555。我们再制定一个协议用于查询目标设备&#x…...
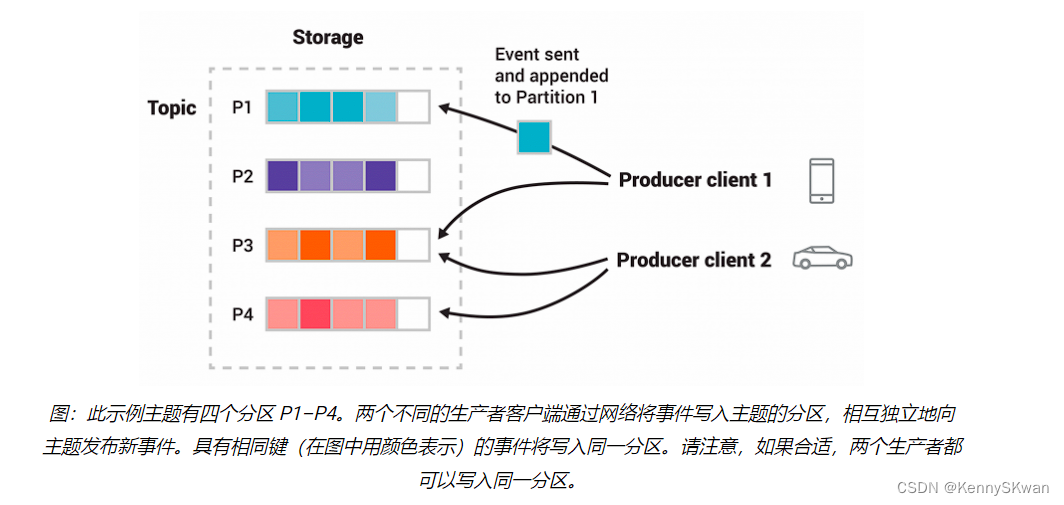
解析Apache Kafka:在大数据体系中的基本概念和核心组件
关联阅读博客文章:探讨在大数据体系中API的通信机制与工作原理 关联阅读博客文章:深入解析大数据体系中的ETL工作原理及常见组件 关联阅读博客文章:深度剖析:计算机集群在大数据体系中的关键角色和技术要点 关联阅读博客文章&a…...
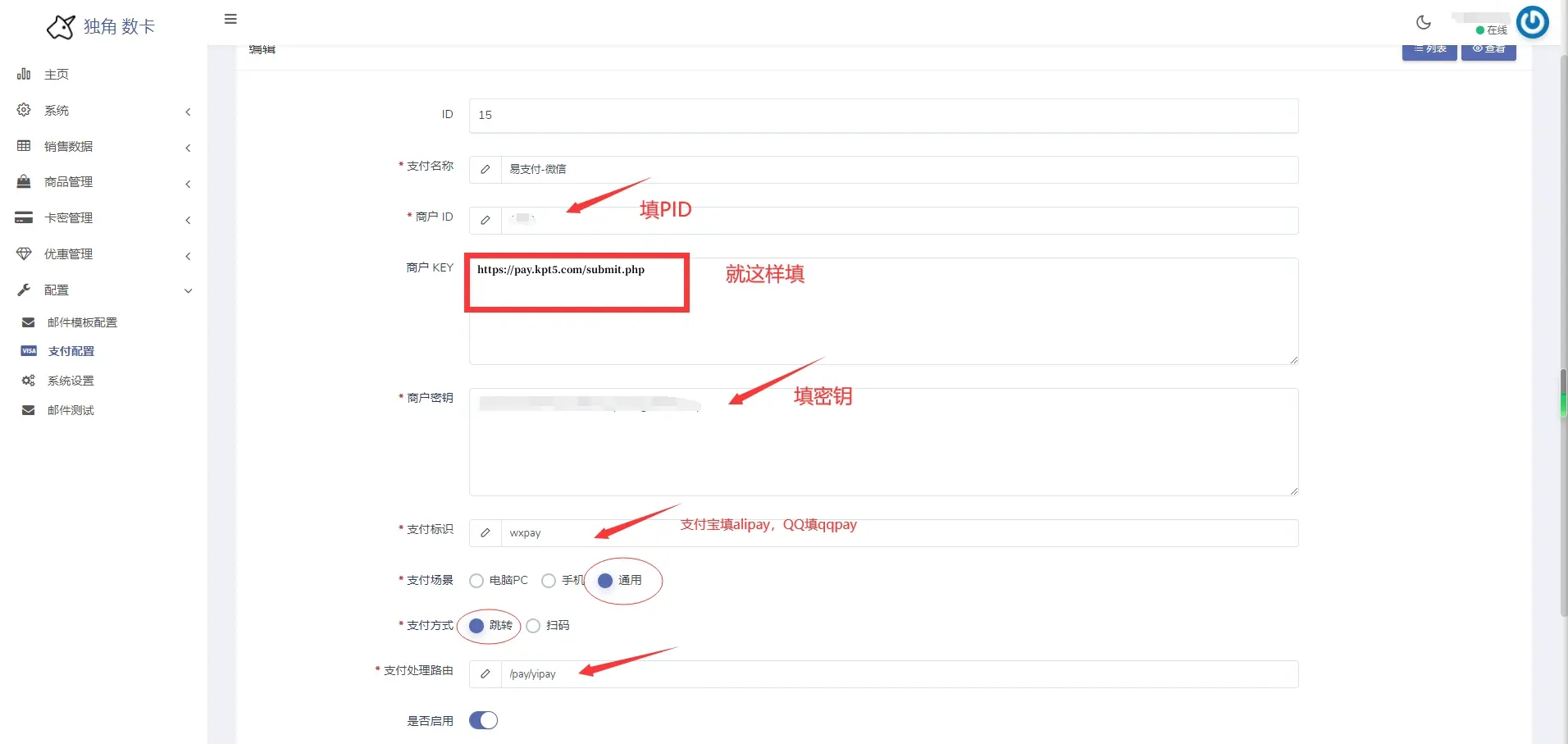
独角数卡对接码支付收款教程
1、到码支付后台找到支付配置。2、将上面的复制依次填入,具体看下图,随后点立即添加 商户ID商户PID 商户KEY异步不能为空 商户密钥商户密钥...
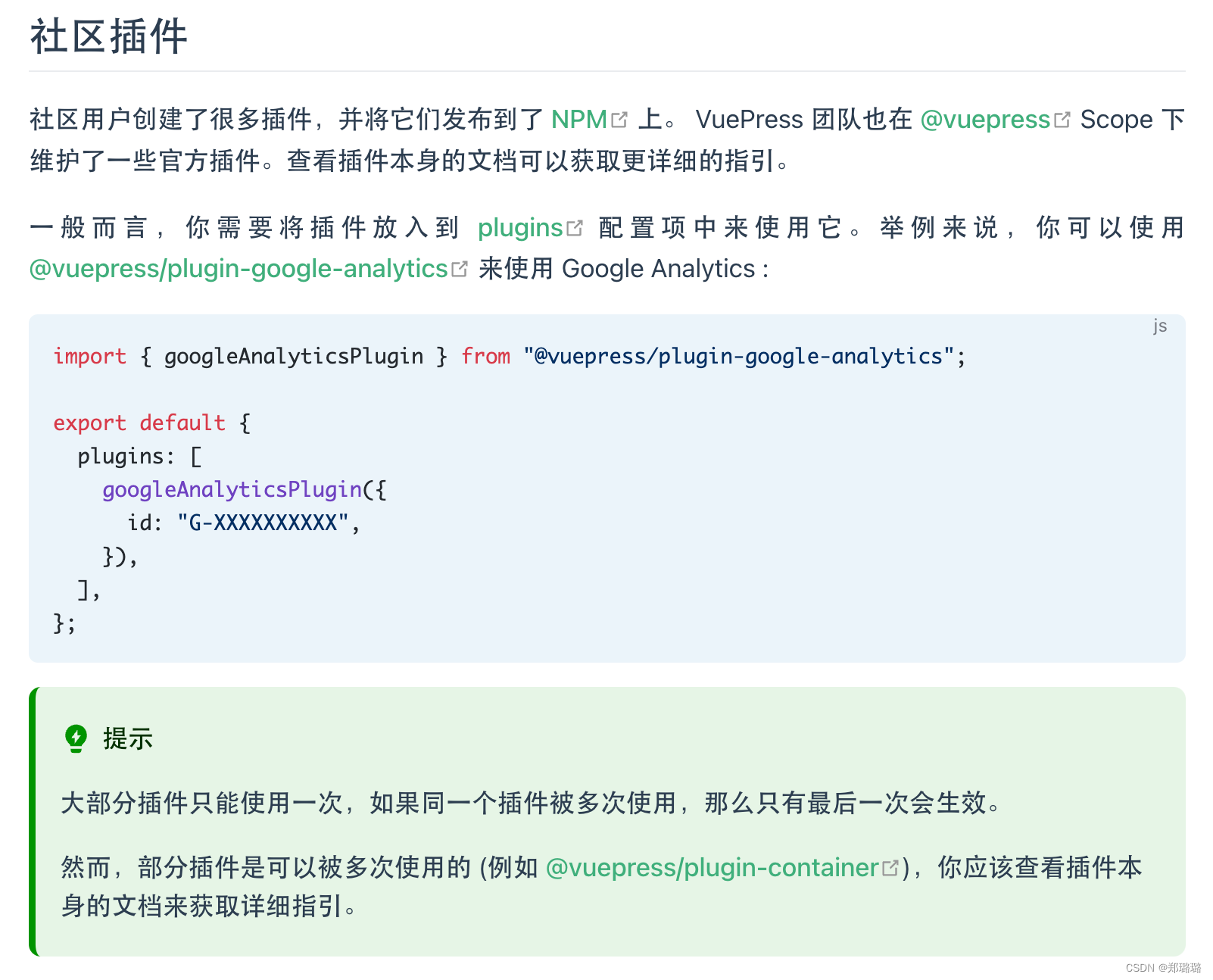
vuepress-theme-hope 添加谷歌统计代码
最近做了个网站,从 cloudflare 来看访问量,过去 30 天访问量竟然有 1.32k 给我整懵逼了,我寻思不应该呀,毕竟这个网站内容还在慢慢补充中,也没告诉别人,怎么就这么多访问?搜索了下, cloudflare 还会把爬虫的请求也就算进来,所以数据相对来说就不是很准确 想到了把 Google An…...

LabVIEW太赫兹波扫描成像系统
LabVIEW太赫兹波扫描成像系统 随着科技的不断发展,太赫兹波成像技术因其非电离性、高穿透性和高分辨率等特点,在生物医学、材料质量无损检测以及公共安全等领域得到了广泛的应用。然而,在实际操作中,封闭性较高的信号采集软件限制…...

什么是stable diffusion?
🌟 Stable Diffusion:一种深度学习文本到图像生成模型 🌟 Stable Diffusion是2022年发布的深度学习文本到图像生成模型,主要用于根据文本的描述产生详细图像。它还可以应用于其他任务,如内补绘制、外补绘制࿰…...
KeyguardClockSwitch的父类
KeyguardClockSwitch 定义在KeyguardStatusView中, mClockView findViewById(R.id.keyguard_clock_container);KeyguardClockSwitch的父类为: Class Name: LinearLayout Class Name: KeyguardStatusView Class Name: NotificationPanelView Class Name: Notificat…...
:Groovy基础)
Gradle系列(二):Groovy基础
Gradle系列(二):Groovy基础 本篇文章继续讲下Groovy一些基础的语法。 1:Map map与List的用法很像,只不过值是一个K:V的键值对。 下面是是Groovy中Map的定义: task testMap { def map [‘width’:1280,‘height’:1960] prin…...

PW1503限流芯片:可达3A限流,保障USB电源管理安全高效
在电源管理领域,开关的性能直接关系到设备的稳定性和安全性。今天,我们将详细解析一款备受关注的超低RDS(ON)开关——PW1503。它不仅具有可编程的电流限制功能,还集成了多项保护机制,为各类电子设备提供了高…...
深挖苹果Find My技术,伦茨科技ST17H6x芯片赋予产品功能
苹果发布AirTag发布以来,大家都更加注重物品的防丢,苹果的 Find My 就可以查找 iPhone、Mac、AirPods、Apple Watch,如今的Find My已经不单单可以查找苹果的设备,随着第三方设备的加入,将丰富Find My Network的版图。产…...

Web3 革命:揭示区块链技术的全新应用
随着数字化时代的不断发展,区块链技术作为一项颠覆性的创新正在改变着我们的世界。而在这一技术的进步中,Web3正逐渐崭露头角,为区块链技术的应用带来了全新的可能性。本文将探讨Web3革命所揭示的区块链技术全新应用,并展望其未来…...

[实战经验]Mybatis的mapper.xml参数#{para}与#{para, jdbcType=BIGINT}有什么区别?
在MyBatis框架中,传入参数使用#{para}和#{para, jdbcTypeBIGINT}的有什么区别呢? #{para}:这种写法表示使用MyBatis自动推断参数类型,并根据参数的Java类型自动匹配数据库对应的类型。例如,如果参数para的Java类型是Lo…...

高并发下的linux优化
针对高并发服务,对 Linux 内核和网络进行优化可以提高系统的性能和稳定性。本文将深入探讨如何对 Linux 内核和网络进行优化,包括调整内核参数、调整网络性能参数、使用 TCP/IP 协议栈加速技术、下面将介绍一些可用于优化Linux内核和网络的技术ÿ…...
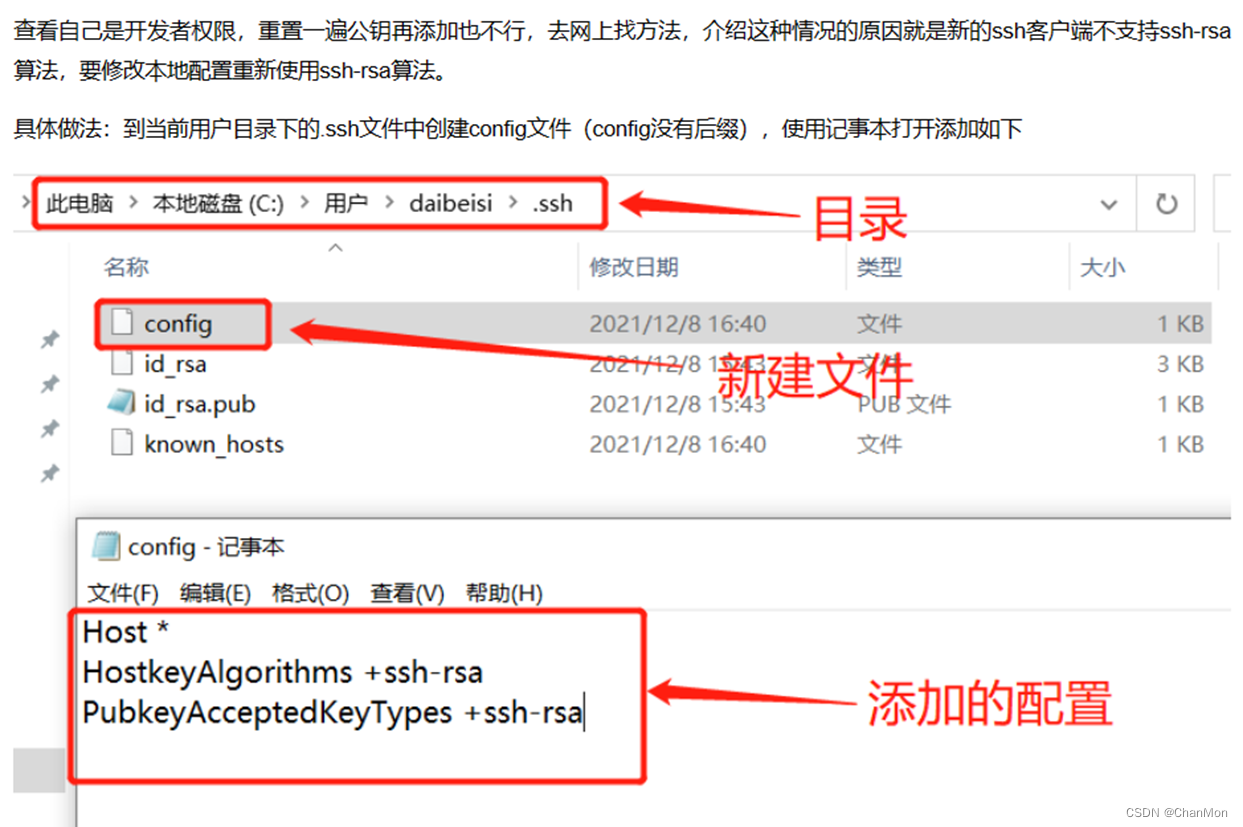
不同设备使用同一个Git账号
想要在公司和家里的电脑上用同一个git账号来pull, push代码 1. 查看原设备的用户名和邮箱 第1种方法, 依次输入 git config user.name git config user.email第2种方法, 输入 cat ~/.gitconfig2. 配置新设备的用户名和邮箱 用户名和邮箱与原设备保持…...

蓝桥杯算法题:区间移位
题目描述 数轴上有n个闭区间:D1,...,Dn。 其中区间Di用一对整数[ai, bi]来描述,满足ai < bi。 已知这些区间的长度之和至少有10000。 所以,通过适当的移动这些区间,你总可以使得他们的“并”覆盖[0, 10000]——也就是说[0, 100…...

提取word文档里面的图片
大家好,我是阿赵。 阿赵我写博客的时候的习惯是,先用word文档写好,然后再把word文档里面的图片另存,最后再在博客里面复制正文和上传图片。 而我写的文章一般配图都比较多,所以经常要做的一个功能就是另存图片…...

MybatisPlus总结
一、MyBatis回顾 (1)什么是MyBatis:MyBatis 是一款优秀的持久层框架,它支持定制化 SQL、存储过程以及高级映射。MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集。MyBatis 可以使用简单的 XML 或注解来配置和映…...

使用 mitmproxy 抓包 grpc
昨天在本地执行 grpc 的 quick start(python版本的),我了解 grpc 内部使用的是 HTTP2,所以我就想着抓包来试试,下面就来记录一下这个过程中的探索。 注意:我的电脑上面安装了 Fiddler Classic,…...

【解决Jetson Nano 内存不足问题】纯命令行将 Conda 环境迁移到 SD 卡
前言 Jetson Nano 板载只有 16GB 的存储空间,在安装完 Ubuntu 和 Conda 环境后,剩余空间就捉襟见肘了,无法满足安装 PyTorch 等大型包的需求。此时如果你有一张SD卡,那么可以考虑将 Conda 环境迁移到 SD 卡上。 但网上的教程基本…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
