LeetCode 378 有序矩阵中第K小的元素
题目信息
LeetoCode地址: . - 力扣(LeetCode)
题解内容大量转载于:. - 力扣(LeetCode)
题目理解
题意很直观,就是求二维矩阵中所有元素排序后第k小的数。
最小堆写法
该写法不再赘述,维护一个大小为k的小顶堆,遍历矩阵所有元素进行入堆操作。
时间复杂度:O(nlogk)
空间复杂度:O(k)
class Solution {public int kthSmallest(int[][] matrix, int k) {PriorityQueue<Integer> heap = new PriorityQueue<>((a,b) -> (int)b-(int)a);for (int i = 0; i<matrix.length; i++) {for (int j = 0; j<matrix[0].length;j++) {if (heap.size() < k) {heap.offer(matrix[i][j]);} else if (matrix[i][j] < heap.peek()) {heap.poll();heap.offer(matrix[i][j]);}}}return heap.peek();}
}二分写法
由于矩阵在行和列上都是有序的,因此左上角的元素matrix[0][0]一定是最小的,右下角的元素matrix[n-1][n-1]一定是最大的。这两个元素,我们分别记为l 和 r.
以下图为例:

可以发现, 任取一个数mid满足l<=mid<=r, 那么矩阵中不大于mid的数,肯定都分布在矩阵的左上角。
例如下图, 取mid=8:
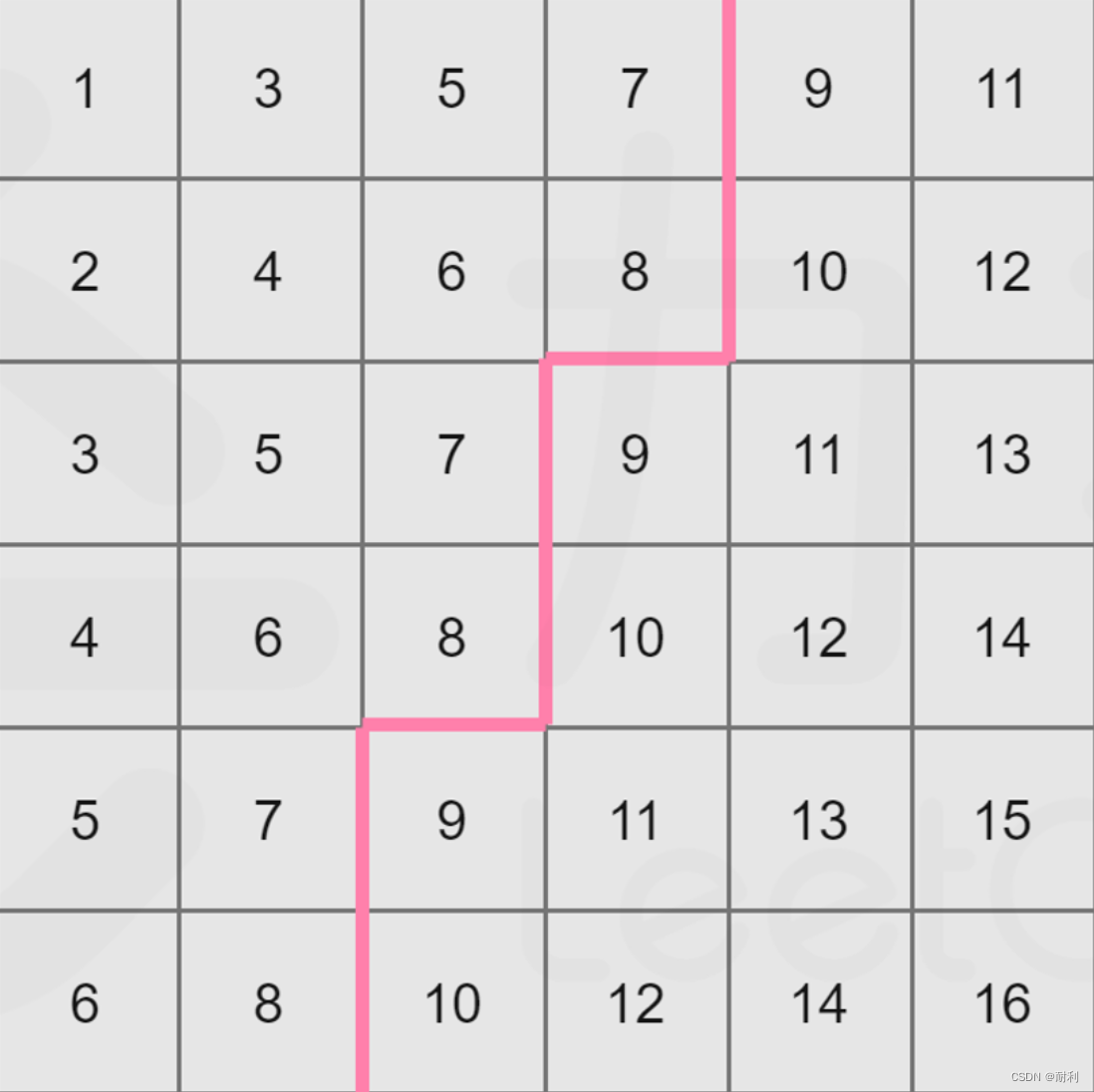
我们可以看出,矩阵中大于mid的数和不大于mid的数分别形成了两个版本,沿着一条锯齿线将这个矩形分隔开。其中左上角板块的大小即为不大于mid的数的数量。
我们只需沿着这条锯齿线走一遍即可计算出这两个板块的大小,自然就统计出这个矩阵中不大于mid的数的个数了。
同样以mid=8举例,走法如下:
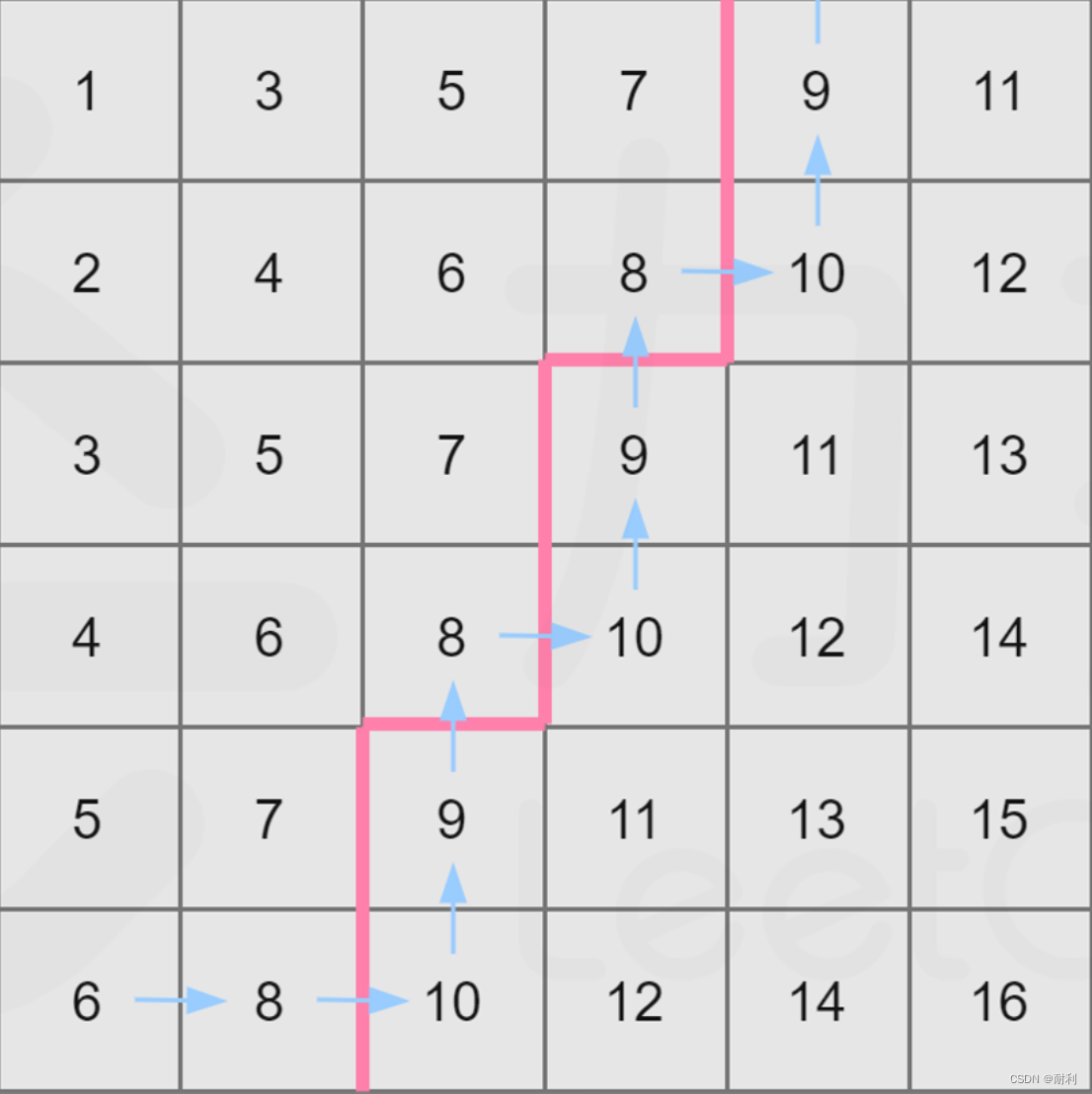
走法可以总结如下:
- 初始位置在matrix[n-1][0] (即左下角);
- 设当前位置为matrix[i][j], 若matrix[i][j] <= mid, 则将当前所在列的不大于mid的数的数量(即i+1)累加到答案中,并向右移动,否则向上移动;
- 不断移动,直到走出格子为止。
可以发现,这样的走法时间复杂度为O(n),即我们可以线性的计算对于任意一个mid,矩阵中有多少数不大于它。这满足了二分查找的性质。
不妨设答案为x, 那么可以直到l<=x<=r, 这样就确定了二分查找的上下界。
对于每次猜测的答案mid, 计算矩阵中有多少数不大于 mid:
- 如果数量不少于k, 那么说明最终答案不大于mid;
- 如果数量小于k, 那么说明最终答案大于mid.
这样我们就可以计算出最终的结果x了。
时间复杂度: O(nlogn)
额外空间复杂度: O(1)
class Solution {public int kthSmallest(int[][] matrix, int k) {int h = matrix.length, w = matrix[0].length;int l = matrix[0][0], r = matrix[h-1][w-1];while (l < r) {int mid = l + (r-l)/2;if (check(matrix, mid, k)) {r = mid;} else {l = mid+1;}}return l;}public boolean check(int[][] matrix,int mid, int k) {int i = matrix.length-1, j = 0;int count = 0;while (i >=0 && j < matrix[0].length) {if (matrix[i][j] <= mid) {count += i+1;j++;} else {i--;}}return count >= k; }
}相关文章:

LeetCode 378 有序矩阵中第K小的元素
题目信息 LeetoCode地址: . - 力扣(LeetCode) 题解内容大量转载于:. - 力扣(LeetCode) 题目理解 题意很直观,就是求二维矩阵中所有元素排序后第k小的数。 最小堆写法 该写法不再赘述,维护…...

Vue3(domdiff)最长递归子序列求解简易版(超简单)
Vue3(domdiff)最长递归子序列求解简易版 ⚠️ 关键词(每一个都需要理解)js 代码实现写完感想欢迎关注 ⚠️ 关键词(每一个都需要理解) 动态规划(O(N^2))(不提倡…...

LLaMA-Factory+qwen多轮对话微调
LLaMA-Factory地址:https://github.com/hiyouga/LLaMA-Factory/blob/main/README_zh.md qwen地址:https://huggingface.co/Qwen/Qwen-7B-Chat/tree/main 数据准备 数据样例 [ {"id": "x3959", "conversations": [{&qu…...

邦芒面试:如何在面试中巧妙回答自己的缺点
在面试中,被问及自己的缺点时,如何巧妙回答是一门学问。恰当的回答不仅能够展示你的自我认知,还能让面试官看到你的成长潜力和积极态度。 首先,切忌谈一些看似缺点实则优点的话题,如追求完美、待人接物太客气等。这些…...

Android:身份证识别功能实现
说明: 此文使用华为SDK、百度SDK、百度在线API三种方式实现。 一、使用华为SDK实现身份证识别: 说明:免费,不需要联网。 1.AndroidManifest.xml添加权限:<uses-permission android:name"android.permissio…...

MacOS安装Homebrew教程
安装 Homebrew 是在 macOS 上管理软件包的一种简便方法。以下是安装 Homebrew 的步骤: 打开终端:你可以通过在 Spotlight 搜索栏中输入“终端”并按下回车键来打开 macOS 的终端应用程序。 执行安装命令:在终端中粘贴以下命令并按下回车键执…...

laravel如何通过DB获取一条数据并转成数组
在 Laravel 中,你可以使用原生数据库查询构建器(DB facade)来获取一条数据,并将其转换为数组。这可以通过在查询链的末尾调用 first() 方法后,使用 toArray() 方法来实现。first() 方法会返回一个 StdClass 对象&#…...
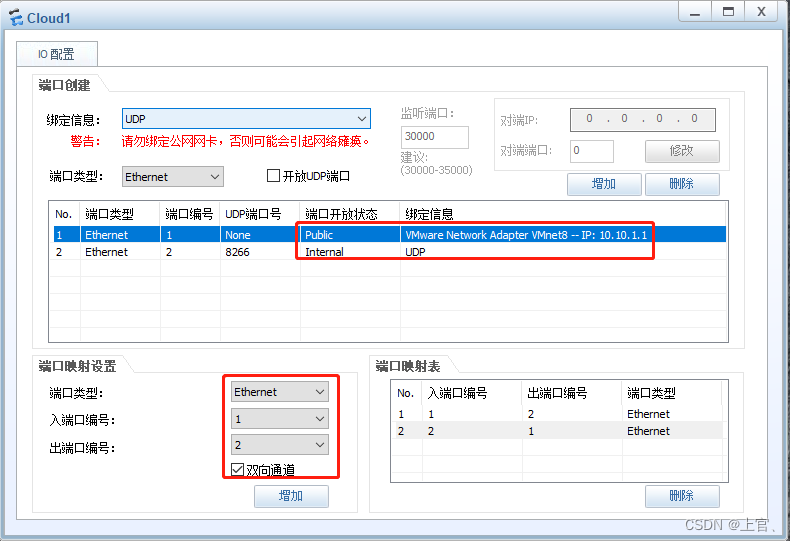
ENSP USG防火墙接入虚拟机;开启Web访问;
1.添加防火墙及云,启动防火墙; 2.配置桥接网卡; 默认账户:admin 默认密码:Admin123 #第一次登陆需修改密码; 默认G0/0/0口为管理口,而在模拟器中进入防火墙的web需如下配置: 配置 …...
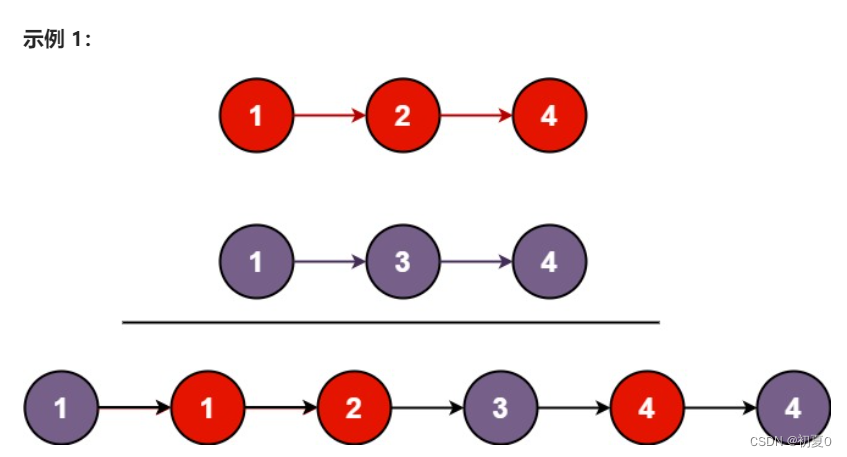
数据结构算法题(力扣)——链表
以下题目建议大家先自己动手练习,再看题解代码。这里只提供一种做法,可能不是最优解。 1. 移除链表元素(OJ链接) 题目描述:给一个链表的头节点 head 和一个整数 val ,删除链表中所有满足值等于 val 的节点…...

LeetCode---391周赛
题目列表 3099. 哈沙德数 3100. 换水问题 II 3101. 交替子数组计数 3102. 最小化曼哈顿距离 一、哈沙德数 简单的模拟题,代码如下 class Solution { public:int sumOfTheDigitsOfHarshadNumber(int x) {int s 0, tmp x;while(tmp){stmp%10;tmp/10;}return x…...

微信小程序的页面交互2
一、自定义属性 (1)定义: 微信小程序中的自定义属性实际上是由data-前缀加上一个自定义属性名组成。 (2)如何获取自定义属性的值? 用到target或currentTarget对象的dataset属性可以获取数据 ÿ…...
【VSCode】修改插件地址
不想放在原始C盘下面C:\Users\{用户}\.vscode\extensions为了后续存储空间考虑,想通过添加环境变量创建名为VSCODE_EXTENSIONS的环境变量,内容指向vs Code扩展所在目录即可 直接配置环境变量,不要在有空格的文件夹下面 变量名称:…...
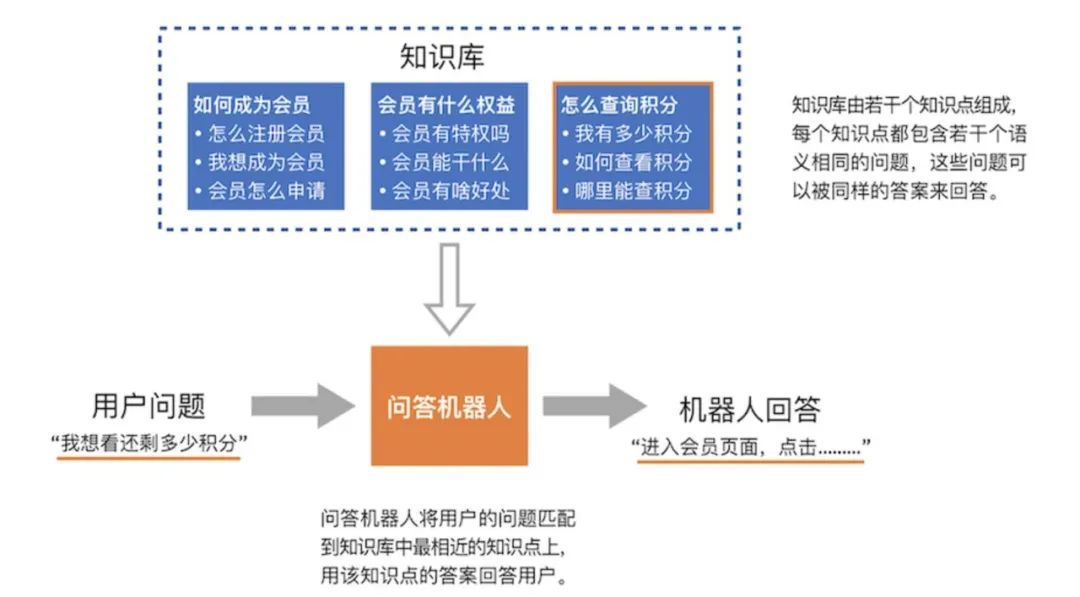
自然语言处理NLP概述
大家好,自然语言处理(NLP)是计算机科学领域与人工智能领域中的一个重要方向,其研究能实现人与计算机之间用自然语言进行有效通信的各种理论和方法。本文将从自然语言处理的本质、原理和应用三个方面,对其进行概述。 一、NLP的本质 NLP是一种…...

计算机网络——37认证
认证 目标:Bob需要Alice证明他的身份 Protocol ap1.0:Alice说"A am Alice" 可能出现的问题: 在网络上Bob看不到Alice,因此Trudy可以简单的声称他是Alice 认证:重新尝试 Protocol ap2.0:Alice…...

Java中利用BitMap位图实现海量级数据去重
🏷️个人主页:牵着猫散步的鼠鼠 🏷️系列专栏:Java全栈-专栏 🏷️个人学习笔记,若有缺误,欢迎评论区指正 目录 前言 什么是BitMap?有什么用? 基本概念 位图的优势 …...

Linux知识点记录
Linux知识点记录 1. 后台运行应用程序方法一:&方法二:nohup & 2. 一个shell脚本中执行多个应用程序3. 2>&14. shell脚本清除日志5. 通过grep查找匹配字符串 1. 后台运行应用程序 参考文章:https://blog.csdn.net/Pan_peter/…...

js的check函数
在JavaScript中,并没有一个内置的名为check的函数。然而,你可以根据需求自定义一个check函数,用于执行各种验证和检查任务。这个check函数的具体作用完全取决于你如何定义和实现它。 以下是一个简单的示例,展示了如何定义一个che…...

赛尼格磁电科技邀您到场参观2024第13届生物发酵展
参展企业介绍 北京赛尼格磁电科技有限公司是一家中加合资的专业永磁组件生产商,2001年成立于中国北京。公司专业从事磁性材料的应用及各类磁系统的设计、开发及制造,公司产品广泛应用于汽车行业、建筑行业、电子行业、航海领域、医学领域、教育领域等。 …...

gpt国内怎么用?最新版本来了
claude 3 opus面世后,这几天已经有许多应用,而其精确以及从不偷懒(截止到2024年3月11日还没有偷懒)的个性,也使得我们可以用它来首次完成各种需要多轮对话的尝试。 今天我们想要进行的一项尝试就是—— 如何从一个不知…...

Vim脚本语言入门:打造你的编辑器
简介 Vim脚本语言是Vim编辑器内置的一种脚本语言,它赋予用户高度的定制和自动化编辑任务的能力。通过编写Vim脚本,用户可以根据自己的需求来扩展和改进Vim编辑器的功能,从而提高编辑效率和舒适度。 在Vim中,脚本语言被广泛用于创…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
